零基础小白都能看懂的一步一步利用BFS解决POJ 迷宫问题代码详解

目录

1.准备

2.代码详解

3.完整代码

---

•  本程序简介：这个代码适合刚接触算法题的小白和新手们，接下来我会一步一步的讲解各代码的明确含义，在文章的最后也会给出完整的代码。

题目说明：可以去搜索引擎直接搜索查找POJ迷宫题目就可以了。

如果对题目了解比较透彻的小伙伴可以直接跳过准备部分进入代码详解部分

用到了队列的数据结构和深度优先搜索（BFS）的算法。

首先明确一点就是BFS一定可以找到最短路径-最优解。

1.准备

1.遍历的顺序约定

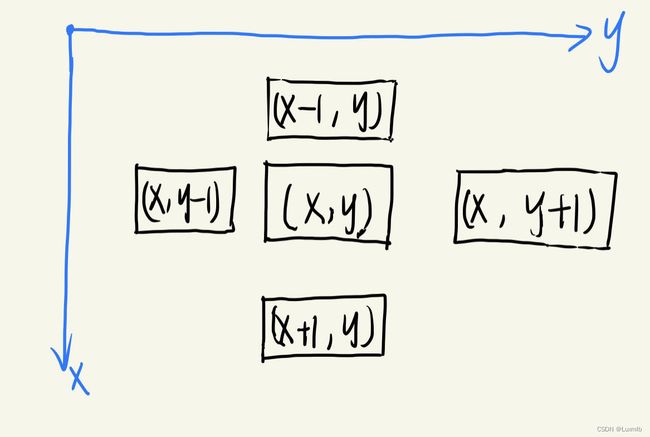
首先我们约定迷宫拓展的顺序是 右 下 左 上 如图所示：

 按照（x,y+1） (x+1,y)  (x,y-1)  (x-1,y)的顺时针的方向顺序遍历

2.迷宫中节点point的类描述

然后我们就要开始描述迷宫中点的特征了：这里我们需要定义一个struct类来表示节点的横坐标x,纵坐标y以及此时距离起点的步长step。

struct piont {
    int x;
    int y;
    int step;  

};

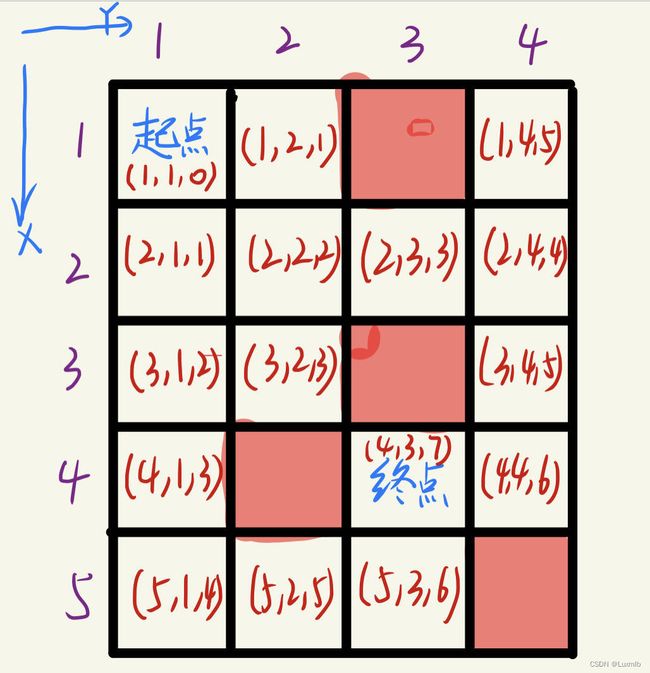
举个例子：如图所示：

起点的状态就是（1，1，0）表示的意思就是起点的位置坐标（起点x坐标为1，起点y坐标为1，距离起点的距离step为0）。

3.队列的使用

用到了stl中的模板 queue ,这个 queue 的元素类型为 point ,也就是步骤2中定义的结构体类型，给它申请一个变量空间 r ;

queuer;

4.队列体现在哪里？

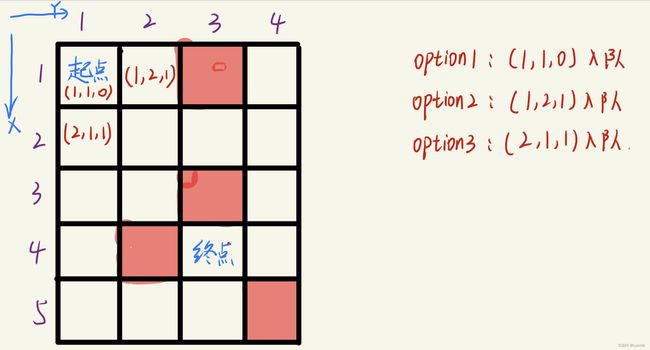
如下图所示：

在以起点（1，1，0）以及其拓展的节点都入队（完成option1到option3）以后，此时起点明显不能继续拓展了，所以我们就要对起点进行出队操作,记住一个原则，拓展的新节点进队，检查不可继续拓展的老节点，如果有，则出队，无，则继续拓展，直到不可拓展。

完成基本的准备工作之后，我们直接进入代码详解释：

2.代码详解

1.题目中的地图用二维数组a表示，因为题目中说明的地图的尺寸是小于等于50X50的所以我开了一个100X100的数组a[100][100]来表示地图的大小。同样的这里面还涉及到了访问，所以开一个访问数组v[100][100]来存储被访问过的节点。

int a[100][100],v[100][100];

2.主体main()函数 

  1.输入：输入行和列，n和m。以及地图。起点坐标（startx,starty）终点坐标（dx,endy）

int main(){
    int n,m,startx,starty,endx,endy;
    scanf("d%d%",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            scanf("%d%d",&a[i][j])
    scanf("d%d%d%d%",&startx,&starty,&endx,&endy);
}

   2.实现BFS

      因为用到的点包含了（x,y,step），因此我们需要准备结构体类型和申请一个队列:

struct piont {
    int x;
    int y;
    int step;  
};
queue r;

     1.起点初始化以及将起点入队

//起点初始化
point start;
start.x=startx;
start.y=starty;
start.step=0;
//起点入队
r.push(start);
//起点入队之后也别忘了将起点设置为已经访问
v[startx][starty]=1;

    2.进行节点拓展：我在准备部分就已经告诉xdm需要注意的是，BFS一定遵循的一个原则就是，队列只要还存在节点就证明这些个存在的节点还没老去，还有拓展的余地，所以每次拓展的同时也要检查老节点是否还可以继续拓展。看注释

//节点拓展
int flag =0;
while(!r.empty()){
   
    int x=r.front().x;
    int y=r.ftont().y;
//判断是不是已经拓展到终点节点了，如果已经到了终点节点就执行break操作
    if(x==endx && y==endy)
    {printf("d%",r.front().step)
        flag=1;
        break
        }
//不是终点节点那么我们就要开始进行拓展
    for(int k=0;k<=3;k++){
        //开两个临时变量用来改变坐标的值
        int tx,ty;

        //x,y开始向规格的遍历顺序进行拓展
        //dx[]={0,1,0,-1} 对应于右 下 左 上
        //dy[]={1,0,-1,0}
        tx=tx+dx[k];
        ty=ty+dy[k];

        //判断这个节点是否可以走而且没有被访问过
        if(a[tx][ty]==1 && v[tx][ty]==0){
        /*由于节点是一个struct类，所以我们需要另开一个temp用来存储临时的节点值，以便将这个temp 
          入队。
        */
        point temp;
        temp.x=tx;
        temp.y=ty;
        temp.step=r.front().step+1; 
        r.push(temp);
        //别忘了将这个点设置为已访问
        v[tx][ty]=1
      }        
   }
//将队首的老节点出队
r.pop();
//拓展完毕
}
//flag只有在到达终点节点的时候才会变为1
if(flag==0){
printf("d%","无可行解")
}

3.完整代码

#include
using namespace std;
int a[100][100],v[100][100];
int dx[]={0,1,0,-1};
int dy[]={1,0,-1,0};
struct point{
	int x;
	int y;
	int step=0;
};
queue r;
int main(){
	int n,m,startx,starty,endx,endy;
	scanf("%d",&n,&m);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			scanf("%d",&a[i][j]);
	scanf("%d",&startx,&starty);
	scanf("%d",&endx,&endy);
	int flag=0;
	point start;
	start.x=startx;
	start.y=starty;
	start.step=0;
	r.push(start);
	v[startx][starty]=1;
while(!r.empty()){
	if(r.front().x==endx && r.front().y==endy){
		flag=1;
		printf("%d",r.front().step);
		break;
	}
	int tx;int ty;
	point temp;
	for(int k=0;k<=3;k++){
		tx=tx+dx[k];
		ty=ty+dy[k];
		if(a[tx][ty]==1 && v[tx][ty]==0){
			temp.x=tx;temp.y=ty;temp.step=r.front().step+1;
			r.push(temp);
			v[tx][ty]=1;
		}
	
	}
	r.pop();
}
if(flag==0)
	scanf("%d","没有正确解");
return 0;
}