STM32实现FFT,求取幅度频谱
STM32实现FFT,求取幅度频谱
FFT不太对劲的理解
FFT的原理比较复杂,因为32使用FFT不用去管算法是如何运作的,我在这里就进行简单的介绍了。
因为是简单介绍,就只介绍下幅度频谱图,不考虑相位频谱图。
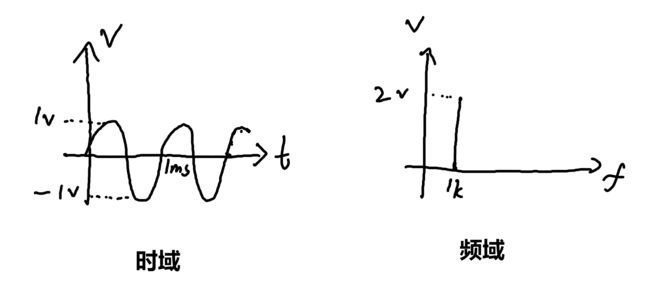
FFT可以将一个信号从时域变换到频域,比如一个1VPP的1k的正弦信号,它的时域和频域的示意图如下:
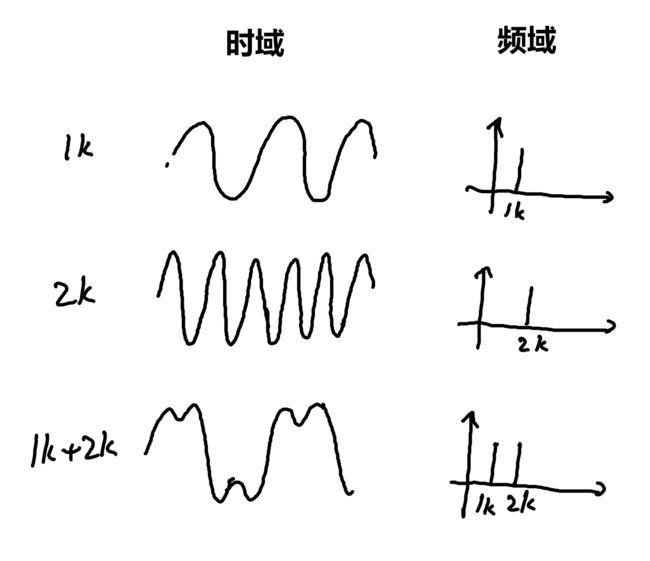
频域为我们观察信号提供了一个新的视角。比如下面是1k和2k信号的叠加。
从时域上看,1k+2k的波形不容易进行处理,也不好猜出来这个波形到底有什么特性(当然这个例子其实还是比较好猜测的,复杂情况就不好看了)。可是变换到频域后,特性非常的明显,处理起来就方便了。
STM32实现FFT
添加DSP库
STM32 DSP库的快速添加 基于cubemx 调用,使用DSP库_四臂西瓜的博客-CSDN博客_cubemx dsp
要采用第二种方法添加DSP,第一种方式添加的DSP库比较老,支持的FFT函数用起来不方便,这篇文章介绍的FFT函数老版本不支持。
设置ADC采集交流+串口重定向
STM32HAL ADC+TIM+DMA采集交流信号 基于cubemx_四臂西瓜的博客-CSDN博客
代码编写
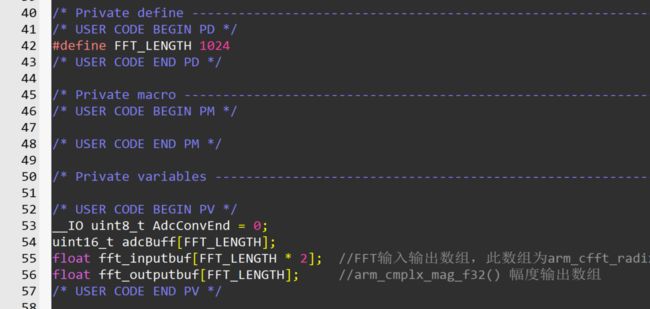
DSP库里面的FFT支持32-4096,同时是 2 n 2^n 2n个整数的傅里叶变换。首先定义下面这些变量。其中只有fft_inputbuf,fft_outputbuf是用来进行FFT的。
#define FFT_LENGTH 1024
__IO uint8_t AdcConvEnd = 0;
uint16_t adcBuff[FFT_LENGTH];
float fft_inputbuf[FFT_LENGTH * 2];
float fft_outputbuf[FFT_LENGTH];
定义完成变量后进行服务内容的书写。首先是ADC进行数据的采集,这一部分再赘述:
HAL_ADCEx_Calibration_Start(&hadc1);
HAL_ADC_Start_DMA(&hadc1, (uint32_t *)adcBuff, FFT_LENGTH);
HAL_TIM_Base_Start(&htim3);
while (!AdcConvEnd) //等待转换完毕
;
傅里叶变换分实数和虚数两种,使用最为频繁的是虚数。我们需要把ADC采集到的数据以虚数的形式存放到傅里叶变换的输入数组fft_inputbuf。虚数的存放方式如下
| 数组下标 | 0 | 1 | 2 | 3 | … |
|---|---|---|---|---|---|
| 数值 | 实部 | 虚部 | 实部 | 虚部 | … |
比如ADC采集到的第二个数据adcBuff[1],它的数据存入到fft_inputbuf[2],它的虚部是fft_inputbuf[3],补零。
我们调用arm_cfft_f32(&arm_cfft_sR_f32_len1024, fft_inputbuf, 0, 1);来对输入数据进行傅里叶变换。它的输入参数含义如下
- arm_cfft_sR_f32_len1024为傅里叶变换结构体,1024是要运算的点数。我们在进行其他点数的计算时,比如说32个点的FFT,就可以用arm_cfft_sR_f32_len32。
- fft_inputbuf为傅里叶变换需要处理的数据的首地址
- 第三个参数0是正变换,1是反变换
- 第四个参数一般是1
经过傅里叶变换后的结果仍然为复数,虚部和实部的比可以计算出频率点的相位,这个在这里不进行考虑。我们直接对复数取模。
取模是实部和虚部的平方和取平均来算,不过我们没必要自己去这样写,因为DSP库为我们提供了取模函数:arm_cmplx_mag_f32(fft_inputbuf, fft_outputbuf, FFT_LENGTH);参数含义如下:
- fft_inputbuf源数据,形式为复数
- fft_outputbuf取完模后的数据,形式为实数
- FFT_LENGTH是取模的点数
他们背后的运算是: f f t o u t p u t b u f [ i ] = f f t i n p u t b u f [ i ∗ 2 ] 2 + f f t i n p u t b u f [ i ∗ 2 + 1 ] 2 fftoutputbuf[i]=\sqrt{fftinputbuf[i*2]^2+fftinputbuf[i*2+1]^2} fftoutputbuf[i]=fftinputbuf[i∗2]2+fftinputbuf[i∗2+1]2
for (int i = 0; i < FFT_LENGTH; i++)
{
fft_inputbuf[i * 2] = adcBuff[i] * 3.3 / 4096;//实部赋值,* 3.3 / 4096是为了将ADC采集到的值转换成实际电压
fft_inputbuf[i * 2 + 1] = 0;//虚部赋值,固定为0.
}
arm_cfft_f32(&arm_cfft_sR_f32_len1024, fft_inputbuf, 0, 1);
arm_cmplx_mag_f32(fft_inputbuf, fft_outputbuf, FFT_LENGTH);
运算完成的结果还需要进行下面的处理,背后的原理就跟FFT算法有关了,这里不做解释。
我们进行的是1024个点的FFT变换,那么fft_outputbuf下标0需要除以1024,其余的数除以512。
fft_outputbuf[0] /= 1024;
for (int i = 1; i < FFT_LENGTH; i++)//输出各次谐波幅值
{
fft_outputbuf[i] /= 512;
}
最后再把运算结果打印出来即可。
printf("FFT Result:\r\n");
for (int i = 0; i < FFT_LENGTH; i++)//输出各次谐波幅值
{
printf("%d:\t%.2f\r\n", i, fft_outputbuf[i]);
}
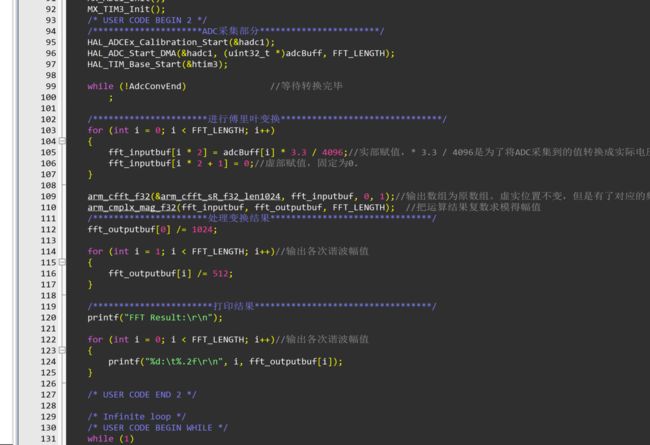
总的代码如下图
运行结果
ADC以100k的频率去采集信号发生器产生的976hz的正弦信号,信号VPP=2v,直流偏置为2V。(注意别超过内部ADC的测量范围0-3.3V)
FFT Result:
0: 1.97
1: 0.00
2: 0.00
3: 0.00
4: 0.00
5: 0.00
6: 0.00
7: 0.00
8: 0.00
9: 0.01
10: 1.05
11: 0.01
12: 0.00
13: 0.00
14: 0.00
...(后面的数据都为0)
结果分析
FFT计算出来的数据是对称的,我们只取前一半的数据,此时的前一半数据是512个。
FFT输出数组的下标表示的频率,计算关系为:
频率 = 数组下标 ∗ 采样率 f f t 计算的点数 频率=数组下标*\frac{采样率}{fft计算的点数} 频率=数组下标∗fft计算的点数采样率
利用这个公式分析下上方的运行结果。数组下标0对应的是0hz,也就是直流偏置,幅度为1.97,和输入信号的2V符合。数组下标10对应的频率为 100 k 1024 ∗ 10 ≈ 976.5 h z \frac{100k}{1024}*10\approx976.5hz 1024100k∗10≈976.5hz,对应幅度为1.05V,和输入信号的2VPP相符。
精度问题
不知道读者有没有注意到待测频率为976hz,而不是我们平时常见的1k,2k?这是为了这个频率正好落在数组下标10点上。10对应的是 100 k 1024 ∗ 10 ≈ 976.5 h z \frac{100k}{1024}*10\approx976.5hz 1024100k∗10≈976.5hz,11对应的 100 k 1024 ∗ 11 ≈ 1075 h z \frac{100k}{1024}*11\approx1075hz 1024100k∗11≈1075hz,1k落在了两点中间,这样就引起了栅栏效应,给人的直观感受就是能量分散了。下面是把待测信号改成1k后的运行结果。
FFT Result:
0: 1.98
1: 0.02
2: 0.03
3: 0.03
4: 0.03
5: 0.04
6: 0.05
7: 0.07
8: 0.10
9: 0.18
10: 0.95
11: 0.30
12: 0.13
13: 0.09
...
可以看到10,11,9等下标都分到了电压(能量)。实际应用中应尽可能避免栅栏效应。
栅栏效应下的补偿
如果不可避免得碰到了栅栏效应,是可以通过数据处理尽可能的还原求取待测信号的幅度值。方法是把频率点附近的能量聚集起来,将附近频率点的幅度平方求和,再取平均。
比如上面1k的情况,就可以把8,9,10,11,12的能量聚集起来。
0. 1 2 + 0.1 8 2 + 0.9 5 2 + 0. 3 2 + 0.1 3 2 = 1.026 \sqrt{0.1^2+0.18^2+0.95^2+0.3^2+0.13^2}=1.026 0.12+0.182+0.952+0.32+0.132=1.026
经过补偿后的幅度值就跟VPP2V真实值更加接近了。
我这里只取了5个点,如果不同主要频率点下标相差比较大,可以取更多;反之更少。
后记
本文章收录于:
唐承乾的电赛小站
本文为系列文章中的冰山一角,欢迎进入小站查看。
配套程序:
STM32进行FFT傅里叶变换——0积分下载