DAY21：二叉树（十一）二叉搜索树中的搜索+验证二叉搜索树（坑比较多，复盘）

700.二叉搜索树中的搜索

• 注意本题迭代法里面涉及的if-else if-else的问题，是比较容易出错的点

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

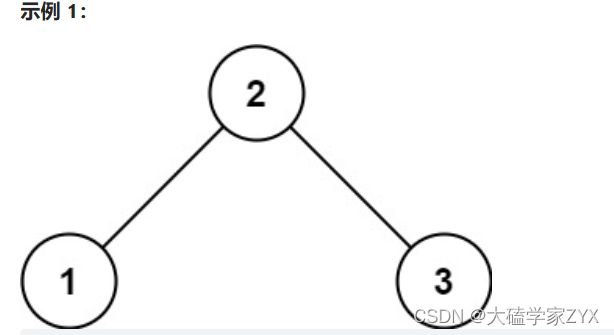
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

输入：root = [4,2,7,1,3], val = 5
输出：[]

提示：

• 数中节点数在 [1, 5000] 范围内
• 1 <= Node.val <= 107
• root 是二叉搜索树
• 1 <= val <= 107

二叉搜索树概念

二叉搜索树是一个有序树：

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉搜索树

这就决定了，二叉搜索树，递归遍历和迭代遍历和普通二叉树都不一样。

可以看前面二叉树理论部分的博客。(10条消息) DAY13：二叉树（一）：二叉树理论基础_大磕学家ZYX的博客-CSDN博客

二叉搜索树是节点便于搜索的树，为了便于搜索，节点是有顺序的。搜索一个节点的时间复杂度是logn。

二叉搜索树中，左子树的所有节点都小于中间节点，右子树的所有节点都大于中间节点。同时，左右子树本身也满足这个规律。下面这两棵树都是二叉搜索树：

二叉搜索树的搜索方式补充

二叉搜索树中：

• 对于任意一个节点，它的左子树中所有节点的值都应该小于这个节点的值。
• 同样地，对于任意一个节点，它的右子树中所有节点的值都应该大于这个节点的值。

注意，这是对每个节点的规定，不仅仅是根节点。这就意味着，在左子树中的右节点，虽然它大于左子树的根节点，但是它依然会小于整个二叉搜索树的根节点（假设它在根节点的左子树里）。同样，在右子树中的左节点，虽然它小于右子树的根节点，但是它依然会大于整个二叉搜索树的根节点（假设它在根节点的右子树里）。

这样的规则使得二叉搜索树可以方便地进行搜索操作：从根节点开始，如果我们要搜索的值小于当前节点，我们就去左子树搜索；如果我们要搜索的值大于当前节点，我们就去右子树搜索。这样可以有效地将搜索范围减半，提高搜索效率。

总结

二叉搜索树对节点的结构没有要求，但是对节点上的元素顺序有要求。

思路

注意在二叉搜索树中，我们不需要强调前中后序。因为二叉搜索树自带顺序。本身是存在规则的，对于每个节点，其节点值比左子树所有元素都要大，比右子树所有元素都要小。这个规则已经确定好搜索方向了。

递归法

• 因为二叉搜索树的有序性，直接判定要搜索的值大小和root的关系就行
• 注意递归返回值的问题

TreeNode* searchTree(TreeNode* root,int val){
    //终止条件
    if(root->val==val){
        return root;
    }
    //单层逻辑
    if(root->val>val){
        return searchTree(root->left,val);
    }
    if(root->val<val){
        return searchTree(root->right,val);
    }
    //如果没有这个节点，就返回NULL
    return nullptr;
}

这么写发生了报错：

Line 16: Char 14: runtime error: member access within null pointer of type 'TreeNode' (solution.cpp)

这个报错是因为递归函数searchTree没有检查root是否为nullptr。这就可能导致当函数递归到树的底部，而树中并没有找到值为val的节点时，函数试图访问空节点（nullptr）的val属性，从而引发运行时错误。

修改为：

TreeNode* searchTree(TreeNode* root, int val){
    // 检查root是否为nullptr
    if(root == nullptr) {
        return nullptr;
    }
	//也可以在这里先定义result==NULL,最后返回result
    //TreeNode* result = nullptr;
    
    // 终止条件
    if(root->val == val) {
        return root;
    }
    // 单层逻辑
    if(root->val > val) {
        return searchTree(root->left, val);
    }
    if(root->val < val) {
        return searchTree(root->right, val);
    }

    // 如果没有这个节点，就直接返回NULL，注意这一句代码并不能代替最开始爹空节点判定！
    return nullptr;
    //return result;
}

如果所有的if都不成立，找不到数值就返回空指针的写法，并不能代替最开始的空节点判定。

• 二叉搜索树BST并不涉及前中后序的问题
• TreeNode* result可以直接赋值nullptr，并不需要堆上new一个新空间

迭代法

• 这种写法是有问题的，此处不能用连续的if语句

TreeNode* searchTree(TreeNode* root, int val){
    //root一直往下遍历
    if(root==nullptr){
        return nullptr;
    }
    while(root!=nullptr){
        //BST确定了搜索方向
        if(val>root->val){
            root = root->right;
        }
        if(val<root->val){
            root = root->left;
        }
        if(val==root->val){
            return root;
        }
    }
    return nullptr;
}

• 因为BST的特性，明确了搜索方向，所以迭代法会比普通二叉树的迭代法简单很多。
• 发生报错：Line 27: Char 23: runtime error: member access within null pointer of type ‘TreeNode’ (solution.cpp)访问了空root

注意这里写if-if和if-else if的区别

如果像上面的写法，我们写if-if，就会发生报错：Line 27: Char 23: runtime error: member access within null pointer of type ‘TreeNode’ (solution.cpp)，也就是说我们访问了空的root。

为什么if-if会访问空的root？

在if语句中我们已经改变了root的值，但是，if-if语句还会继续执行if(root->val>val)的判断！

如果root->right->left是空指针，那么if-if结构继续执行if(valval)的时候，就会发生访问空指针的val的问题，会发生报错。

if-if结构和if-else if-else的区别

• 连着的if-if语句和if-else if-else的区别就是，if-if会执行完一个if之后，继续进行下一个的if判断。而else if结构中，所有的if语句块只会执行其中一个，执行完了一个之后，跳过后面所有的if语句块。

迭代法修改结果：

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
    if(root==nullptr){
        return nullptr;
    }
    //root一直往下遍历
    while(root!=nullptr){
        //BST确定了搜索方向
        if(val>root->val){
            root = root->right;
        }
        else if(val<root->val){
            root = root->left;
        }
        //注意这里else不需要加条件了，加条件会编译错误
        else{
            return root;
        }
    }
    return nullptr;

    }
};

当我们在代码中使用一系列的 if 语句时，每个 if 语句都会被评估。即使前一个 if 语句的条件满足并执行了其内部的代码块，后面的 if 语句仍会被检查。如果其条件也满足，它的代码块也会被执行。

但是在 if-else if-else 结构中，只有一个代码块会被执行。首先，会检查 if 语句的条件。如果它满足，就执行其内部的代码块，并跳过所有的 else if 和 else。如果 if 语句的条件不满足，就检查第一个 else if 语句的条件。这个过程会继续，直到找到一个满足的条件，或者所有的 if 和 else if 都被检查过。如果所有的 if 和 else if 的条件都不满足，且存在 else 语句，那么就会执行 else 内部的代码块。

因此，if-else if-else 结构常常被用于多种互斥情况的判断，即这些情况不能同时发生。而 if-if 结构则适用于多种条件可以同时满足的情况。

98.验证二叉搜索树（坑比较多，注意复盘）

• 本题重点是给你一个二叉树，直接用中序遍历判定树是不是单调递增的。
• 遇到二叉搜索树一定要想起中序遍历得到单调递增有序元素值的特性。
• 注意空的二叉树和只有一个节点的二叉树，都属于二叉搜索树！
• 这道题坑很多，建议定期回来重写一下

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

输入：root = [2,1,3]
输出：true

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

思路

判断一棵树是不是二叉搜索树，主要看节点是不是满足大小条件。

遍历顺序方面，我们最好选择中序遍历，因为中序遍历是左中右，BST中大小关系是对于任意一个节点，左子树节点全部小于该节点，右子树节点全部大于该节点。

也就是说，按照左中右来遍历，我们会得到一个从小到大的有序数组。

• 遇到二叉搜索树类型题目一定要用到特性，就是中序遍历的话，得到的元素是有序的！

写法1：中序遍历得到数组判断是否单调递增

伪代码

• 空二叉树属于所有二叉树类型，什么类型都是true

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        //终止条件
        if(root==NULL){
            return true;//空二叉树，属于所有二叉树类型
        }
        vector<int>nums;
        //中序遍历
        //左
        isValidBST(root->left);
        //nums.push_back(root->left->val);
        //注意这里左节点和右节点是不需要单独放进数组的，因为会遍历到！
        
        //中的逻辑：把正在遍历的节点放进数组里
        nums.push_back(root->val);
        
        //右
        isValidBST(root->right);
        //nums.push_back(root->right->val);
        
        //判断数组是否有序，有序返回true
        
        
    }
};

这种写法，是把二叉树转变成一个Nums数组，然后判断数组是否有序，来看是不是BST。

实际上，我们没有必要把二叉树转变为一个数组！遍历的过程直接就可以判断元素是不是递增的。

也就是说，可以利用中序遍历，直接判断传入的二叉树是不是单调递增的。

完整版

• BST不允许相等元素
• 注意单调递增判断的时候，for循环一定要从i=1开始，因为取初值的时候nums[0]已经是初值了！如果相等就会直接返回false！
• 注意单调递增的判断方式

class Solution {
public:
    vector<int>result;
    //单独写遍历，再在主函数中判断result是不是单调递增
    void travelsal(TreeNode* root){
        if(root==NULL){
            return;
        }
        //左
        travelsal(root->left);
        //中：加入数组
        result.push_back(root->val);
        //右
        travelsal(root->right);
    }
    
    bool isValidBST(TreeNode* root) {
        travelsal(root);
        //先数组判空
        if(result.empty()){
            return true;
        }
        //单调递增判断
        int value = result[0];
        //这里的i一定要从1开始而不是0，因为初始值已经是nums[0]了！
        for(int i=1;i<result.size();i++){
            //BST中不允许相等元素，等于也是false
            if(result[i]<=value){
                return false;
            }
            //更新数值
            value = result[i];
        }
        return true;
    }
};

写法2：不单独创建数组的方法

• 这种写法是直接判断二叉树是不是单调递增，不另外创建任何数组，不占用其余空间

判断节点顺序的误区

如果"中"的逻辑这么写

if(root->val > root->left->val&&root->val < root->right->val){
    return true;
}

这种写法是有问题的，因为BST，根节点需要不仅比左孩子大，需要比整个左子树的节点都要大！但是这种写法只判断了根节点<右孩子，并没有判断根节点是不是大于所有右子树的节点。

例如：

上图这个例子，如果单独来看根节点，每个根节点都满足>左孩子，<右孩子。

但是，根节点10是小于它的右孩子的左节点6的。

也就是说这么写的话，遇到上图的情况判断是失效的。

伪代码

class Solution {
public:
    //定义一个全局变量，因为提示里面树元素值范围是2^31，因此定义int也可以
    //但是这里必须定义long long，因为节点内部会出现int的最小值，想要更新数值的话，必须比int的最小值还要小！
    //定义小于INT_MIN的值，为了更新数值
    long long maxValue = LONG_MIN;
    
    bool isValidBST(TreeNode* root) {
        //终止条件
        if(root==NULL){
            return true;
        }
        //左
        bool left = isValidBST(root->left);
        //中：比较节点
        if(root->val > maxValue){
            maxValue = root->val;//maxValue记录了当前节点前一个的数值，如果是BST那么每次都会更新数值
        }
        else{
            //如果当前节点小于上一个节点，说明已经不满足单调递增了
            return false;
        }
        //右
        bool right = isValidBST(root->left);
        if(left&&right){
            return true;
        }
        return false;

    }
};

完整版

• 这种情况，如果maxValue定义成了int，那么，输入[0]的时候，输出会是false。

class Solution {
public:
    //这里int是错误的必须定义long long
    //int maxValue = LONG_MIN;
    long long maxValue = LONG_MIN;
    bool isValidBST(TreeNode* root) {
        //终止条件
        if(root==nullptr){
            return true;
        }
        //中序遍历
        //左
        bool left = isValidBST(root->left);
        //中
        if(root->val > maxValue){
            //更新最大值
            maxValue = root->val;
        }
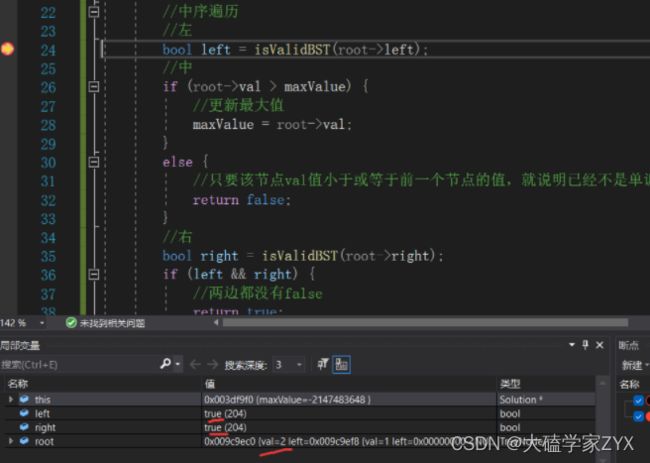
        else{
            //只要该节点val值小于或等于前一个节点的值，就说明已经不是单调递增了！
            return false;
        }
        //右
        bool right = isValidBST(root->right);
        if(left&&right){
            //两边都没有false
            return true;
        }
        return false;  
    }
};

int和long long数据范围的问题

在 C++ 中，int 和 long long 的范围依赖于具体的编译器和运行环境。但通常，int 在 32 位系统中的范围是 -2^31 到 2^31 - 1（即 -2147483648 到 2147483647），在 64 位系统中的范围通常与 32 位系统一致；而 long long 的范围则是 -2^63 到 2^63 - 1（即 -9223372036854775808 到 9223372036854775807）。

本题树节点的范围是 -2^31 <= Node.val <= 2^31 - 1，那么我们就可以使用 int 来保存树元素的值。因为这个范围内的所有整数都在 int 的范围内。

当需要处理的整数可能超过 int 的范围时，应该使用 long long。例如，如果在计算过程中可能产生大于 2^31 - 1 或小于 -2^31 的结果，或者需要处理的数据就已经超过了这个范围，那么就应该使用 long long。

本题maxValue必须定义成long long的原因

因为本题的树元素值里面，包含了INT_MIN（也就是-2^31），因此如果想要更新maxValue里面的数值，使得maxValue一直是节点值，就必须定义的比树中的最小数值INT_MIN更小，也就是定义long long。

如果把maxValue定义成INT_MIN，那么如果第一个节点值就是-2^31的话，if(root->val > maxValue)就不会满足条件，就会直接return false！

debug问题：如果maxValue定义成int，输入[0]的时候为什么不对？

原因是发生了类型截断，此时int变量因为接收了long long类型，导致int型的maxValue = 0。

具体详见博客：cpp比较坑的问题：int maxValue = LONG_MIN；会发生截断_大磕学家ZYX的博客-CSDN博客

递归root->left传入会不会直接返回true的问题

问题：递归传入**isValidBST(root->left); root->left如果是空的，不会导致终止条件 if(root==nullptr) return true;直接返回true了吗？**

如果root->left和root->right都是空的，也满足二叉搜索树定义。

当对空节点（nullptr）调用 isValidBST 函数时，函数确实会返回 true。

但是，从逻辑上来讲，没有孩子的子节点本身就是二叉搜索树。如果一棵树只有一个节点，那么这棵树也是二叉搜索树。

当函数传入root->left返回true，这并不意味着整个函数会立即结束并返回 true。而是意味着对 isValidBST(root->left) 的调用返回了 true，代码将继续执行，并进一步检查当前节点的值是否大于 maxValue，以及是否可以在右子树上进行有效的 BST 检查。

我们可以试着使用debug功能跟踪代码在处理二叉树 [2,1,3]（一个有效的 BST）时的行为。当对根节点（值为 2）调用 isValidBST 函数时，首先会对左子节点（值为 1）调用 isValidBST。因为左子节点没有孩子，而没有孩子的子节点本身就是BST！所以 isValidBST(root->left) 和 isValidBST(root->right) 都会返回 true，并且 1 会被正确地设为新的 maxValue。然后，你的代码将返回到对根节点的调用，并继续检查根节点的值是否大于当前的 maxValue（即 1），并对右子节点（值为 3）进行类似的检查。

所以，当递归调用遇到一个空节点时，虽然 isValidBST(root->left) 或 isValidBST(root->right) 会返回 true，但这并不会导致整个函数立即返回 true。

写法3：不定义初始值，用指针进行优化

如果修改本题目的数据范围，变成long long的话，写法2这种定义初值maxValue的方式就不能用了。

那么此时我们只能对前一个节点和后一个节点进行比较。写法如下：

• 用新指针pre记录前一个节点，注意pre->val的访问涉及pre判空的问题

• 注意BST必须单调递增，前后元素相等也不行

• 由于pre的初始值是nullptr，又有直接取pre的值val的操作，所以必须先判定pre是不是空！

伪代码

class Solution {
public:
    //定义一个pre节点,记录当前遍历的前一个节点
    //中的逻辑重新写一下
    TreeNode* pre = nullptr;
    
    bool isValidBST(TreeNode* root) {
        //终止条件
        if(root==NULL){
            return true;
        }
        //左
        bool left = isValidBST(root->left);
        //中：比较节点
        //这里要加 = ，等于也不行
        if(pre!=nullptr&&pre->val >= root->val){
           return false;
        }
        else{
            //pre数值更新
            pre->val = root->val;
        }
        //右
        bool right = isValidBST(root->left);
        if(left&&right){
            return true;
        }
        return false;

    }
};

完整版

• 这种写法，<=的错误判断需要放在if里，因为最开始指针就是nullptr！

class Solution {
public:
    //定义存放前一个节点的指针
    TreeNode* pre = nullptr;
    bool isValidBST(TreeNode* root) {
        if(root==nullptr){
            return true;
        }
        //左
        bool left = isValidBST(root->left);
        //中，nullptr本身并没有val值，需要先判断是不是空的
        //这种写法，错误判断需要放在if里，因为最开始指针就是nullptr！
        if(pre!=nullptr&&root->val <= pre->val){
            return false;
        }
        else{
            //更新数值
            pre = root;
        }
        //右
        bool right = isValidBST(root->right);
        if(left&&right){
            return true;
        }
        return false;
    }
};

双指针思想

后一个比前一个大，更新指针，这种思想实质上就是双指针思想。双指针之前整理过不少题目，可以复习一下。

pre必须事先判定是否为空

代码里涉及到了取pre->val的操作，而pre初始值为空！所以取值之前一定要先看是不是空指针！否则依然会编译出错。

Line 23: Char 29: runtime error: member access within null pointer of type ‘TreeNode’ (solution.cpp)

只要涉及到TreeNode*指针取值的操作，就一定要看指针是不是空的。