postgreSQL源码分析——索引的建立与使用——B-Tree索引（1）

2021SC@SDUSC

本篇博客我们先讲讲B-Tree的算法实现原理和相关的数据结构

B-Tree索引算法介绍

// nbtree.c
 * nbtree.c
 *Implementation of Lehman and Yao's btree management algorithm for
 *Postgres.

nbtree算法是在lehman和Yao所撰写的论文的基础上形成的，多用于数据库索引，B-Tree索引实在B+树上的变形，首先我们下来讲解一下B+树：

B+树

B+树为B树的变形，B+内部有两种结点，一种是索引结点，一种是叶子结点；B+树的索引结点并不会保存记录，用于索引，而叶子结点用于保存数据。这样做的好处是在找一个范围的数据时时间更快，不会像B树一样一个一个的搜索；

Lehman and Yao’s btree

在lehman和Yao的论文中，对于B+树做了改进，主要结构如下
B+tree每个节点都额外增加一个‘rightlink’指向它的右邻居结点。允许btree的操作并发执行，后续再根据rightlink来复原出完整的btree。另外还设置highkey,设置了元组的最大范围，他对于后面的并发查找插入有很大的作用，在后面会进行举例讲解。b-link-tree的算法实现有效减少了锁的使用，加快了数据库查找，插入的效率，并发性也有很大提高。我们接下来举例具体讲解一下该树的具体如何实现。

rightlink

每个结点都有一个指向右边结点的指针，当B-link-tree建立的时候都叶子结点会有两个指针指向，一个是父结点的指针，一个是左邻居指针。这样做的好处是当插入一个节点时，叶子结点分裂，父结点还没更新，查找依然还可以通过左邻居指针找到。
我画了一个简略的图示，刚开始的状态如图所示父结点指向叶子结点，当进行查找操作时，会对a上锁，根据范围找到y，对a解锁。
如过此时进行插入操作，则可能会发生分裂，y会有指向y’的指针，此时查找操作再次找y会有可能出现找不到的情况，通过rightlink则会找到y’，找到自己想要的数据。rightlink的实现提高了数据库的并发性，在这种算法没实现之前，会对父子节点都进行上锁，显然没有rightlink更好。

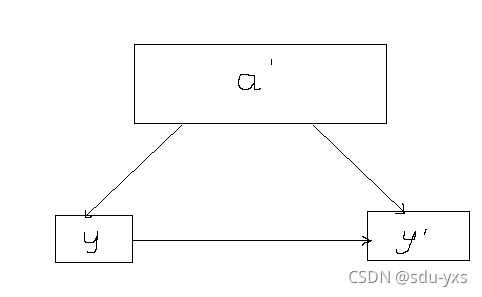
highkey

highkey的实现是为了判断是否产生分裂，上述过程中当查找操作时搜索父节点时，节点A发生了分裂，新分裂出来的节点B还没来得及插入到父节点中，进程1根据错误的分裂之前节点A在父节点的highkey进入到了老的A节点，而A节点的highkey在分裂时发生发生了变化，从父节点的追随过来的highkey比节点A上看到的highkey要大，说明从父节点descend到子节点过程中一定发生了分裂。

pg的B-Tree索引

pg的B-Tree算法在Lehman and Yao’s btree 上做了一些改变，不仅仅向右的指针，也有向左的指针，这样实现了正向和反向的扫描。
同时让我们结合图示来理解B-Tree索引的实现过程：
postgresql的索引数据结构如下：

如图所示，完成页面填充之后

当完成页面填充时，linp0并没有赋值，会根据情况进行更进一步的操作，当前节点分为两种情况：
1.当前节点不是最右边节点：linp0记录该节点的highkey，指向该节点，如图中

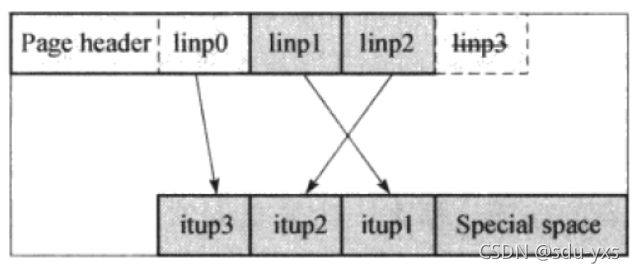
2.当前节点为最右侧节点：不需要记录highkey，将所有的linp依次递减

以上就是postgresql的B-Tree的基本实现原理，接下来我们来讲解一下关于B-Tree的数据结构。

B-Tree数据结构

在nbtree.h中我们找到了关于索引节点的数据结构,我将其中的理解写在里面：

BTPageOpaqueData

// nbtree.h

typedef struct BTPageOpaqueData
{
	BlockNumber btpo_prev;		/* 左兄弟的块号，便于反向扫描 */
	BlockNumber btpo_next;		/* 右兄弟的块号，正向扫描*/
	union
	{
		uint32		level;		/* 在索引树中的层级level*/
		TransactionId xact;		/* 删除无用的ID */
	}			btpo;
	uint16		btpo_flags;		/* 页面类型 */
	BTCycleId	btpo_cycleid;	/* vacuum cycle ID of latest split */
} BTPageOpaqueData;

还有些与BTPageOpaqueData相关的宏定义：

// 
/* Bits defined in btpo_flags */
#define BTP_LEAF		(1 << 0)	/* 有该标志表明有叶子页面 */
#define BTP_ROOT		(1 << 1)	/* 根页面*/
#define BTP_DELETED		(1 << 2)	/* 从索引树中删除的页面 */
#define BTP_META		(1 << 3)	/* 元页面*/
#define BTP_HALF_DEAD	(1 << 4)	/* 空页面，但仍保留*/
#define BTP_SPLIT_END	(1 << 5)	/* rightmost page of split group */
#define BTP_HAS_GARBAGE (1 << 6)	/* page has LP_DEAD tuples，LP——DEAD元组 */
#define BTP_INCOMPLETE_SPLIT (1 << 7)	/* right sibling's downlink is missing */

BTMetaPageData

而其中也介绍了meta page的相关结构，这是所必须有的，它指向root page所在的id:

//meta page
typedef struct BTMetaPageData
{
	uint32		btm_magic;		/* 包括BTREE_MAGIC */
	uint32		btm_version;	/* B-Tree的版本 (always <= BTREE_VERSION) */
	BlockNumber btm_root;		/* 正确的root page的序号 */
	uint32		btm_level;		/* root  page在书中的层级 */
	BlockNumber btm_fastroot;	/* current "fast" root location */
	uint32		btm_fastlevel;	/* tree level of the "fast" root page */
	TransactionId btm_oldest_btpo_xact;
	float8		btm_last_cleanup_num_heap_tuples;	//对应堆
} BTMetaPageData;

nbtree.c也定义了一些相关的数据结构

BTVacState

//nbtree建立时所需要的工作空间和数据，与锁，空余页等有关
typedef struct
{
	IndexVacuumInfo *info;
	IndexBulkDeleteResult *stats;
	IndexBulkDeleteCallback callback;
	void	   *callback_state;
	BTCycleId	cycleid;
	BlockNumber lastBlockVacuumed;	//最高的已被清除的锁号
	BlockNumber lastBlockLocked;	//最高的加上锁的锁号
	BlockNumber totFreePages;	/* 空余页*/
	TransactionId oldestBtpoXact;
	MemoryContext pagedelcontext;
} BTVacState;

BTParallelScanDescData

以下是并行扫描的相关数据结构，是nbtree比较重要的部分

// 
typedef struct BTParallelScanDescData
{
	BlockNumber btps_scanPage;	/* 最近被搜索的page */
	BTPS_State	btps_pageStatus;	/* 指出下一个可搜索的page */
	int			btps_arrayKeyCount; /* 并行扫描处理的key数*/
	slock_t		btps_mutex;		/* 用lock来保护变量 */
	ConditionVariable btps_cv;	/*  */
}			BTParallelScanDescData;

下一章我们会讲解nbtree的建立，搜索等相关操作的数据结构和函数。