Java-数据结构-并查集＜二＞

一.并查集的简单介绍

二. 并查集的主要构成和实现方式

三.HashMap模板和数组模板

由于在下文的模板基本一致，不再每次都罗列，大体的模板如下，若有错误可以在leetcode找到对应的题目解答，已经附上连接。

HashMap

class UnionFind {
    private Map father;
    
    public UnionFind() {
        father = new HashMap();
    }
    
    public void add(int x) {
        if (!father.containsKey(x)) {
            father.put(x, null);
        }
    }
    
    public void merge(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        
        if (rootX != rootY){
            father.put(rootX,rootY);
        }
    }
    
    public int find(int x) {
        int root = x;
        
        while(father.get(root) != null){
            root = father.get(root);
        }
        
        while(x != root){
            int original_father = father.get(x);
            father.put(x,root);
            x = original_father;
        }
        
        return root;
    }
    
    public boolean isConnected(int x, int y) {
        return find(x) == find(y);
    }
}

数组

class UnionFind{
    public int[] parent;
    public int count;
    //初始化
    public UnionFind(int n){
        parent = new int[n];
        count = n;
        for(int i = 0; i< n; i++){
            parent[i] = i;
        }
    }
    //查找
    public int find(int x){
        while(x != parent[x]){
            parent[x] = parent[parent[x]];
            x = parent[x];
        }
        return x;
    }
    //合并节点
    public void union(int x, int y){
        if(find(x) == find(y)) return;
        parent[find(x)] = find(y);
        count--;
    }
    //是否为同一父节点,也就是是否联通
    public boolean isConnected(int x, int y){
        return find(x) == find(y);
    }
    //返回数量
    public int getCount(){
        return count;
    }
}

三. leetcode实战

1. leetcode547 省份数量

2. leetcode684 冗余连接

以上未出现部分圈全在在前篇文章，不再赘述

Java-数据结构-并查集＜一＞

3. leetcode1905 统计子岛屿

给你两个 m x n 的二进制矩阵 grid1 和 grid2 ，它们只包含 0 （表示水域）和 1 （表示陆地）。一个 岛屿 是由 四个方向 （水平或者竖直）上相邻的 1 组成的区域。任何矩阵以外的区域都视为水域。

如果 grid2 的一个岛屿，被 grid1 的一个岛屿 完全 包含，也就是说 grid2 中该岛屿的每一个格子都被 grid1 中同一个岛屿完全包含，那么我们称 grid2 中的这个岛屿为 子岛屿 。

请你返回 grid2 中 子岛屿 的 数目 。

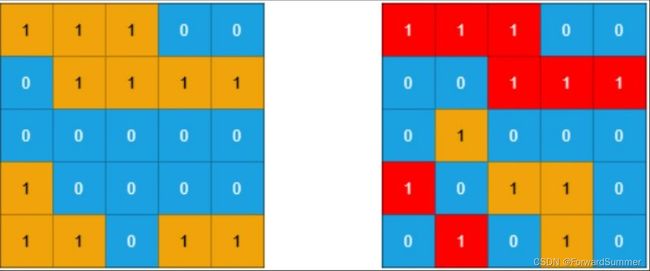
输入：grid1 = [[1,1,1,0,0],[0,1,1,1,1],[0,0,0,0,0],[1,0,0,0,0],[1,1,0,1,1]], grid2 = [[1,1,1,0,0],[0,0,1,1,1],[0,1,0,0,0],[1,0,1,1,0],[0,1,0,1,0]]
输出：3
解释：如上图所示，左边为 grid1 ，右边为 grid2 。
grid2 中标红的 1 区域是子岛屿，总共有 3 个子岛屿。

 

整体思路：

1.遍历grid2数组，利用并查集把区域都连通起来
2.将grid的根节点都添加到HashSet中
3.到grid1中找HashSet中对应的节点是不是1

以示例一为例

那么，在使用并查集后，我们的un2里面陆地联通的区域就是：
0,11,15,17,21
那么对应的HashSet里面也会是{0,11,15,17,21}
然后遍历grid1，找到HashSet对应的位置，是1的话，就可以符合题目要求。
HashSet中的11是不符合要求的，因为对应的grid1里面是0，同样
HashSet中的17也是同样的道理。 

主题函数部分（模板在上方）

class Solution {
    public int countSubIslands(int[][] grid1, int[][] grid2) {
        int row1 = grid1.length;
        int col1 = grid1[0].length;
        int row2 = grid2.length;
        int col2 = grid2[0].length;
        UnionFind un2 = new UnionFind(row2*col2);
        //遍历grid2
        for(int i = 0; i < row2; i++){
            for(int j = 0; j < col2; j++){
                if(grid2[i][j] == 0) continue;
                if(i+1 < row2 && grid2[i+1][j] == 1) un2.union(i*col2+j, i*col2+j+col2);
                if(j+1 < col2 && grid2[i][j+1] == 1) un2.union(i*col2+j, i*col2+j+1);
            }
        }
        //把grid2联通区域的根节点放进set中
        HashSet set = new HashSet<>();
        for(int i = 0; i < row2; i++){
            for(int j = 0; j < col2; j++){
                if(grid2[i][j] == 1){
                    set.add(un2.find(i*col2+j));
                }     
            }
        }
        //去grid1查找对应的点是不是1
        for(int i = 0; i < row1; i++){
            for(int j = 0; j < col1; j++){
                 if(grid1[i][j] == 0){
                    set.remove(un2.find(i*col2+j));
            }    
            }
        }
       return set.size();
    }
}

 原题解连接（若模板有出入可参考）：

Java 并查集 超简单易懂附模板

 

4. leetcode1254 统计封闭岛屿的数目

二维矩阵 grid 由 0 （土地）和 1 （水）组成。岛是由最大的4个方向连通的 0 组成的群，封闭岛是一个 完全 由1包围（左、上、右、下）的岛。

请返回 封闭岛屿 的数目。

示例 1：
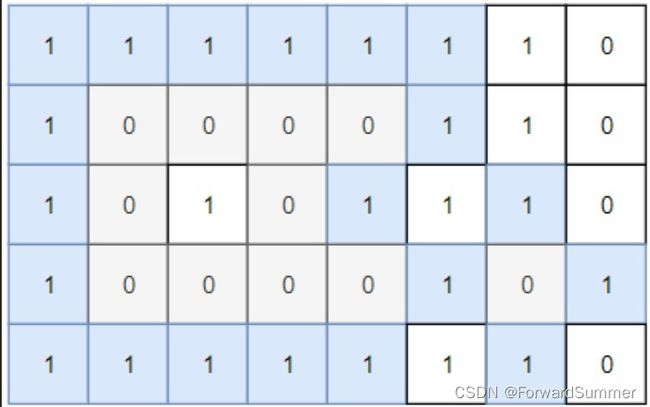
输入：grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
输出：2
解释：
灰色区域的岛屿是封闭岛屿，因为这座岛屿完全被水域包围（即被 1 区域包围）。

 

 整体思路

1. 用并查集走一遍grid，把岛屿都联通起来
2. 用HashSet添加岛屿的根节点
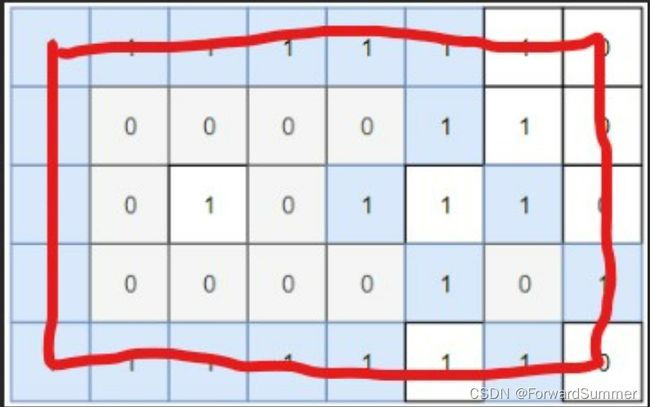
3. 把处于边上，也就是下图中红色部分排除掉（注意，此时排除的是对应是陆地的那个节点的根节点）

 也就是

if(grid[i][j] == 0){
    if(i == 0 || j == 0 || i == row-1 || j == col -1) set.remove(un.find(i*col+j));    
}

主函数中

if(i == 0 || j == 0 || i == row-1 || j == col -1)

可以排除掉图中红色的部分。

主函数部分

class Solution {
    public int closedIsland(int[][] grid) {
        int row = grid.length;
        int col = grid[0].length;
        UnionFind un = new UnionFind(row*col);
        for(int i = 0; i < row; i++){
            for(int j = 0; j < col; j++){
                if(grid[i][j] == 1) continue;
                if(i+1 < row && grid[i+1][j] == 0) un.union(i*col+j, i*col+j+col);
                if(j+1 < col && grid[i][j+1] == 0) un.union(i*col+j, i*col+j+1);
            }
        }
        HashSet set = new HashSet<>();
        for(int i = 0; i < row; i++){
            for(int j = 0; j < col; j++){
                if(grid[i][j] == 0) set.add(un.find(i*col+j));    
            }
        }
        for(int i = 0; i < row; i++){
            for(int j = 0; j < col; j++){
                if(grid[i][j] == 0){
                    if(i == 0 || j == 0 || i == row-1 || j == col -1) set.remove(un.find(i*col+j));    
                }
            }
        }
        return set.size();
    }
}

原题解连接（若模板有出入可参考）：
Java 并查集 思路简单附模板

 

5. leetcode130 被围绕的区域

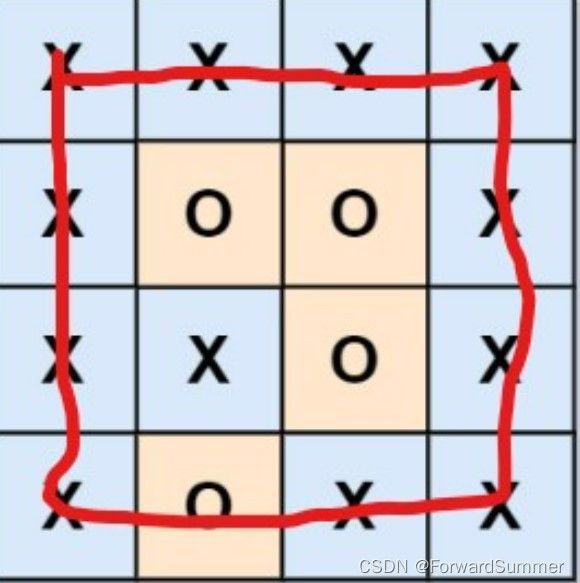
给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例 1：
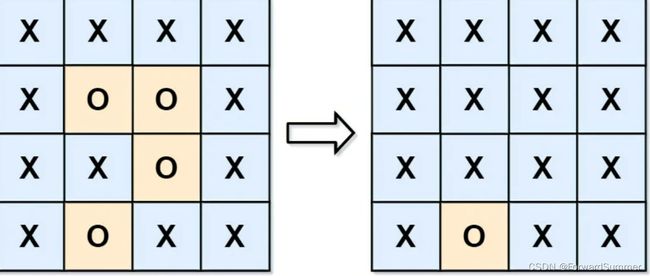
输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 
任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。
如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

整体思路:

1.这题和1254. 统计封闭岛屿的数目思路一样
2.只不过要的是外面的岛屿，而1254里要的是里卖的。

思路

1. 并查集走一遍，得到所有的父节点
2. 把所有的父节点添加到set中
3. 把边上的所有的岛排除掉（即排除边上的是'O'的父节点）（即下图红色的部分从set中排除）
4. 把剩在set中的父节点中的是'O'的都变成'X'

主函数

class Solution {
    public void solve(char[][] board) {
        int row = board.length;
        int col = board[0].length;
        UnionFind un = new UnionFind(row*col);
        for(int i = 0; i < row; i++){
            for(int j = 0; j < col; j++){
                if(board[i][j] == 'X') continue;
                if(i+1 < row && board[i+1][j] == 'O') un.union(i*col+j, i*col+j+col);
                if(j+1 < col && board[i][j+1] == 'O') un.union(i*col+j, i*col+j+1);
            }
        }
         HashSet set = new HashSet<>();
        for(int i = 0; i < row; i++){
            for(int j = 0; j < col; j++){
                if(board[i][j] == 'O'){
                    set.add(un.find(i*col +j));
                }
            }
        }
        for(int i = 0; i < row; i++){
            for(int j = 0; j < col; j++){
                if(board[i][j] == 'O'){
                    if(i == 0 || j == 0 || i == row-1 || j == col-1){
                    set.remove(un.find(i*col +j));
                    }
                }
            }
        }
        for(int i = 0; i < row; i++){
            for(int j = 0; j < col; j++){
                if(board[i][j] == 'O'){
                    if(set.contains(un.find(i*col +j))){
                        board[i][j] = 'X';
                    }
                }
            }
        }
    }
}

原题解连接（若模板有出入可参考）：

Java 并查集 思路简单附模板

6. leetcode1319 连通网络的操作次数

用以太网线缆将 n 台计算机连接成一个网络，计算机的编号从 0 到 n-1。线缆用 connections 表示，其中 connections[i] = [a, b] 连接了计算机 a 和 b。

网络中的任何一台计算机都可以通过网络直接或者间接访问同一个网络中其他任意一台计算机。

给你这个计算机网络的初始布线 connections，你可以拔开任意两台直连计算机之间的线缆，并用它连接一对未直连的计算机。请你计算并返回使所有计算机都连通所需的最少操作次数。如果不可能，则返回 -1 。

输入：n = 4, connections = [[0,1],[0,2],[1,2]]
输出：1
解释：拔下计算机 1 和 2 之间的线缆，并将它插到计算机 1 和 3 上。

 思路：

1. 我们总共有的线的数量就是connections数组的数量
2. 连接n个电脑我们最少需要n-1条线
3. 并查集过后我们把已经连接的电脑看作一个整体m，如果线够用的情况下我们只需要m-1条线，不必在意具体要怎么连接

以示例2为例

示例 2：
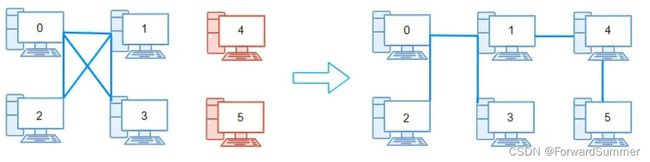
输入：n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
输出：2

那么在并查集过后，并查集的数量是3，减一就可以得到我们需要的答案。

主函数

class Solution {
    public int makeConnected(int n, int[][] connections) {
        int len = connections.length;
        if(len < n-1) return -1;
        UnionFind un = new UnionFind(n);
        for(int i = 0; i < len; i++){
            un.union(connections[i][0],connections[i][1]);
        }
        return un.getcount()-1;
    }
}

原题解连接（若模板有出入可参考）：

Java 并查集 简单易懂附模板