theano入门学习

theano入门学习

原文地址：http://blog.csdn.NET/hjimce/article/details/46806923

作者:hjimce

本篇博文主要是在我刚入门学theano的一个学习历程的回顾，记录了自己深度学习学习征程的第一站。

一、初识theano

1、theano.tensor常用数据类型

学习theano，首先要学的就是theano.tensor使用，其是基础数据结构，功能类似于Python.numpy，教程网站为：http://deeplearning.net/software/theano/library/tensor/basic.html

在theano.tensor数据类型中，有double、int、uchar、float等各种类型，不过我们最常用到的是int和float类型，float是因为GPU一般是float32类型，所以在编写程序的时候，我们很少用到double，常用的数据类型如下：

数值：iscalar(int类型的变量)、fscalar(float类型的变量)

一维向量：ivector(int 类型的向量)、fvector(float类型的向量)、

二维矩阵：fmatrix(float类型矩阵)、imatrix（int类型的矩阵）

三维float类型矩阵：ftensor3  

四维float类型矩阵：ftensor4

其它类型只要把首字母变一下就可以了，更多类型请参考：http://deeplearning.net/software/theano/library/tensor/basic.html#theano.tensor.TensorVariable 中的数据类型表格

2、theano编程风格

例1：记得刚接触theano的时候，觉得它的编程风格很神奇，与我们之前所接触到的编程方式大不相同。在c++或者Java等语言中，比如我们要计算“2的3次方”的时候，我们一般是：

 int x=2;
 int y=power(x,3);

也就是以前的编程方法中，我们一般先为自变量赋值，然后再把这个自变量作为函数的输入，进行计算因变量。然而在theano中，我们一般是先声明自变量x(不需要赋值)，然后编写函数方程结束后；最后在为自变量赋值，计算出函数的输出值y，比如上面的代码在theano中，一般这么写：

 import theano
 x=theano.tensor.iscalar('x')#声明一个int类型的变量x
 y=theano.tensor.pow(x,3)#定义y=x^3
 f=theano.function([x],y)#定义函数的自变量为x（输入），因变量为y（输出）
 print f(2)#计算当x=2的时候，函数f(x)的值
 print f(4)#计算当x=4时，函数f(x)=x^3的值

一旦我们定义了f(x)=x^3，这个时候，我们就可以输入我们想要的x值，然后计算出x的三次方了。因此个人感觉theano的编程方式，跟我们数学思路一样，数学上一般是给定一个自变量x，定义一个函数(因变量)，然后根据我们实际的x值，对因变量进行赋值。在深度学习中，每个样本就是一个x的不同赋值。

例2：S函数示例。再看一个例子，S函数的实现：

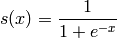
 import theano
 x =theano.tensor.fscalar('x')#定义一个float类型的变量x
 y= 1 / (1 + theano.tensor.exp(-x))#定义变量y
 f= theano.function([x],y)#定义函数f，输入为x，输出为y
 print f(3)#计算当x=3的时候，y的值

上面的例子中，我们学到了一个非常重要的函数:theano.function,这个函数用于定义一个函数的自变量、因变量。

function网站为：http://deeplearning.net/software/theano/library/compile/function.html。函数的参数：function(inputs, outputs, mode=None, updates=None, givens=None, no_default_updates=False, accept_inplace=False, name=None,rebuild_strict=True, allow_input_downcast=None, profile=None, on_unused_input='raise')，参数看起来一大堆，不过我们一般只用到三个，inputs表示自变量、outputs表示函数的因变量(也就是函数的返回值)，还有另外一个比较常用的是updates这个参数，这个一般用于神经网络共享变量参数更新，这个参数后面讲解。

例3：function使用示例

我们再看一个多个自变量、同时又有多个因变量的函数定义例子：

 #coding=utf-8
 import theano
 x, y =theano.tensor.fscalars('x', 'y')
 z1= x + y
 z2=x*y
 f =theano.function([x,y],[z1,z2])#定义x、y为自变量，z1、z2为函数返回值（因变量）
 print f(2,3)#返回当x=2，y=3的时候，函数f的因变量z1，z2的值

二、必学函数

例1、求偏导数

theano有个很好用的函数，就是求函数的偏导数theano.grad()，比如上面的S函数，我们要求当x=3的时候，s函数的导数，代码如下：

 #coding=utf-8
 import theano
 x =theano.tensor.fscalar('x')#定义一个float类型的变量x
 y= 1 / (1 + theano.tensor.exp(-x))#定义变量y
 dx=theano.grad(y,x)#偏导数函数
 f= theano.function([x],dx)#定义函数f，输入为x，输出为s函数的偏导数
 print f(3)#计算当x=3的时候，函数y的偏导数

例2、共享变量

共享变量是多线程编程中的一个名词，故名思议就是各线程，公共拥有的变量，这个是为了多线程高效计算、访问而使用的变量。因为深度学习中，我们整个计算过程基本上是多线程计算的，于是就需要用到共享变量。在程序中，我们一般把神经网络的参数W、b等定义为共享变量，因为网络的参数，基本上是每个线程都需要访问的。

 #coding=utf-8
 import theano
 import numpy
 A=numpy.random.randn(3,4);#随机生成一个矩阵
 x = theano.shared(A)#从A，创建共享变量x
 print x.get_value()

通过get_value()、set_value()可以查看、设置共享变量的数值。

例3、共享变量参数更新

前面我们提到theano.function函数，有个非常重要的参数updates，updates是一个包含两个元素的列表或tuple，updates=[old_w,new_w]，当函数被调用的时候，这个会用new_w替换old_w,具体看一下下面例子：

 #coding=utf-8
 import theano
 w= theano.shared(1)#定义一个共享变量w，其初始值为1
 x=theano.tensor.iscalar('x')
 f=theano.function([x], w, updates=[[w, w+x]])#定义函数自变量为x，因变量为w，当函数执行完毕后，更新参数w=w+x
 print f(3)#函数输出为w
 print w.get_value()#这个时候可以看到w=w+x为4

这个主要用于梯度下降的时候，要用到。比如updates=[w,w-α*(dT/dw)]，其中dT/dw就是我们梯度下降的时候，损失函数对参数w的偏导数，α是学习率。

OK，下面开始进入实战阶段，实战阶段的源码主要参考自网站：http://deeplearning.net/tutorial/

三、实战阶段1—逻辑回归实现

打好了基础的扎马步阶段，接着我们就要开始进入学习实战招式了，先学一招最简答的招式，逻辑回归的实现：

 #coding=utf-8
 import numpy
 import theano
 import theano.tensor as T
 rng = numpy.random

 N = 10     # 我们为了测试，自己生成10个样本，每个样本是3维的向量，然后用于训练
 feats = 3
 D = (rng.randn(N, feats).astype(numpy.float32), rng.randint(size=N, low=0, high=2).astype(numpy.float32))


 # 声明自变量x、以及每个样本对应的标签y(训练标签)
 x = T.matrix("x")
 y = T.vector("y")

 #随机初始化参数w、b=0，为共享变量
 w = theano.shared(rng.randn(feats), name="w")
 b = theano.shared(0., name="b")

 #构造损失函数
 p_1 = 1 / (1 + T.exp(-T.dot(x, w) - b))   # s激活函数
 xent = -y * T.log(p_1) - (1-y) * T.log(1-p_1) # 交叉商损失函数
 cost = xent.mean() + 0.01 * (w ** 2).sum()# 损失函数的平均值+L2正则项，其中权重衰减系数为0.01
 gw, gb = T.grad(cost, [w, b])             #对总损失函数求参数的偏导数

 prediction = p_1 > 0.5                    # 预测

 train = theano.function(inputs=[x,y],outputs=[prediction, xent],updates=((w, w - 0.1 * gw), (b, b - 0.1 * gb)))#训练所需函数
 predict = theano.function(inputs=[x], outputs=prediction)#测试阶段函数

 #训练
 training_steps = 1000
 for i in range(training_steps):
     pred, err = train(D[0], D[1])
     print err.mean()#查看损失函数下降变化过程

四、实战阶段2—mlp实现

接着学一个稍微牛逼一点，也就三层神经网络模型的实现，然后用于“手写字体识别”训练：

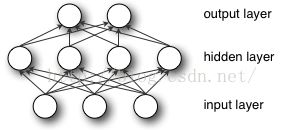
网络输出层的计算公式就是：

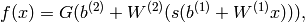
具体源码如下：

 #encoding:utf-8
 import os
 import sys
 import timeit
 import numpy
 import theano
 import theano.tensor as T
 from logistic_sgd import LogisticRegression, load_data


 class HiddenLayer(object):
     def __init__(self, rng, input, n_in, n_out, W=None, b=None,
                  activation=T.tanh):
         """
         2、rng: numpy.random.RandomState是随机数生成器用于初始化W
         3、input: 类型为theano.tensor.dmatrix，是一个二维的矩阵(n_examples, n_in)
         第一维表示训练样本的个数，第二维表示特征维数，比如:input(i,j)表示第i个样本的第j个特征值
         4、n_in: 输入特征数，也就是输入神经元的个数
         5、n_out: 输出神经元的个数
         6、W如果有输入，那么为(n_in,n_out)大小的矩阵
         7、b如果有输入，那么为(n_out,)的向量
         8、activation活激活函数选项

         """
         self.input = input


         '''''W的初始化选择[-a,a]进行均匀分布采样，其中如果激活函数选择tanh，则a=sqrt(6./(本层输入神经元数+本层输出神经元数))
         如果激活函数是选择sigmoid，那么a=4*sqrt(6./(本层输入神经元数+本层输出神经元数))
         dtype类型需要设置成theano.config.floatX，这样GPU才能调用'''
         if W is None:#如果外部没有输入W，那么创建W
             W_values = numpy.asarray(
                 rng.uniform(
                     low=-numpy.sqrt(6. / (n_in + n_out)),
                     high=numpy.sqrt(6. / (n_in + n_out)),
                     size=(n_in, n_out)
                 ),
                 dtype=theano.config.floatX
             )
             if activation == theano.tensor.nnet.sigmoid:
                 W_values *= 4

             W = theano.shared(value=W_values, name='W', borrow=True)

         if b is None:#如果外部没有输入b，那么创建b
             b_values = numpy.zeros((n_out,), dtype=theano.config.floatX)
             b = theano.shared(value=b_values, name='b', borrow=True)

         self.W = W
         self.b = b
         #激活函数映射
         lin_output = T.dot(input, self.W) + self.b
         self.output = (
             lin_output if activation is None
             else activation(lin_output)
         )
         # 模型参数
         self.params = [self.W, self.b]


 # MLP类是三层神经网络：输入，隐层，输出，第一层为简单的人工神经网络，第二层为逻辑回归层
 class MLP(object):

     def __init__(self, rng, input, n_in, n_hidden, n_out):
         """
         n_in: 输入层神经元个数

         n_hidden: 隐层神经元个数

         n_out:输出层神经元个数

         """

         # 创建隐藏层
         self.hiddenLayer = HiddenLayer(
             rng=rng,
             input=input,
             n_in=n_in,
             n_out=n_hidden,
             activation=T.tanh
         )

         # 创建逻辑回归层
         self.logRegressionLayer = LogisticRegression(
             input=self.hiddenLayer.output,
             n_in=n_hidden,
             n_out=n_out
         )

         # 整个网络的L1正则项，也就是使得所有的链接权值W的绝对值总和最小化
         self.L1 = (
             abs(self.hiddenLayer.W).sum()
             + abs(self.logRegressionLayer.W).sum()
         )

         # 整个网络的L2正则项，也就是使得所有的链接权值的平方和最小化
         self.L2_sqr = (
             (self.hiddenLayer.W ** 2).sum()
             + (self.logRegressionLayer.W ** 2).sum()
         )

         #
         self.negative_log_likelihood = (
             self.logRegressionLayer.negative_log_likelihood
         )
         # same holds for the function computing the number of errors
         self.errors = self.logRegressionLayer.errors

         # 把所有的参数保存到同一个列表中，这样后面可以直接求导
         self.params = self.hiddenLayer.params + self.logRegressionLayer.params

         self.input = input

 #手写数字识别测试，BP算法
 def test_mlp(learning_rate=0.01, L1_reg=0.00, L2_reg=0.0001, n_epochs=1000,
              dataset='mnist.pkl.gz', batch_size=20, n_hidden=500):
     """
     learning_rate: 梯度下降法的学习率

     L1_reg: L1正则项的权值

     L2_reg:L2正则项的权值

     n_epochs:最大迭代次数

     dataset：里面的数据是28*28的手写图片数据

    """
     datasets = load_data(dataset)

     train_set_x, train_set_y = datasets[0]
     valid_set_x, valid_set_y = datasets[1]
     test_set_x, test_set_y = datasets[2]

     # 批量训练，计算总共有多少批
     n_train_batches = train_set_x.get_value(borrow=True).shape[0] / batch_size
     n_valid_batches = valid_set_x.get_value(borrow=True).shape[0] / batch_size
     n_test_batches = test_set_x.get_value(borrow=True).shape[0] / batch_size



     # 分配符号变量
     index = T.lscalar()  # index to a [mini]batch
     x = T.matrix('x')  # 训练数据
     y = T.ivector('y')  # 训练数据的标签

     rng = numpy.random.RandomState(1234)

     # 构建三层神经网络
     classifier = MLP(
         rng=rng,
         input=x,
         n_in=28 * 28,
         n_hidden=n_hidden,
         n_out=10
     )

     # 计算损失函数
     cost = (
         classifier.negative_log_likelihood(y)
         + L1_reg * classifier.L1
         + L2_reg * classifier.L2_sqr
     )
     #损失函数求解偏导数
     gparams = [T.grad(cost, param) for param in classifier.params]
     # 梯度下降法参数更新
     updates = [
         (param, param - learning_rate * gparam)
         for param, gparam in zip(classifier.params, gparams)
     ]


     #定义训练函数
     train_model = theano.function(
         inputs=[index],
         outputs=cost,
         updates=updates,
         givens={
             x: train_set_x[index * batch_size: (index + 1) * batch_size],
             y: train_set_y[index * batch_size: (index + 1) * batch_size]
         }
     )

     #跑起来，训练起来，搞起
     epoch=0
     while (epoch <10):
         cost=0
         for minibatch_index in xrange(n_train_batches):
             cost+= train_model(minibatch_index)
         print 'epoch:',epoch,'    error:',cost/n_train_batches
         epoch = epoch + 1


 #跑起来，网络train起来
 test_mlp()

五、实战阶段3—最简单的卷积神经网络实现

最后再学一招最牛逼的，也就是卷积神经网络的实现，下面是一个手写字体lenet5的实现：

 #-*-coding:utf-8-*-
 import theano
 import numpy as np
 import matplotlib.pyplot as plt
 from loaddata import loadmnist
 import theano.tensor as T


 #softmax函数
 class softmax:
     #outdata为我们标注的输出，hiddata网络输出层的输入，nin,nout为输入、输出神经元个数
     def __init__(self,hiddata,outdata,nin,nout):

         self.w=theano.shared(value=np.zeros((nin,nout),dtype=theano.config.floatX),name='w');
         self.b=theano.shared(value=np.zeros((nout,),dtype=theano.config.floatX),name='b')

         prey=T.nnet.softmax(T.dot(hiddata,self.w)+self.b)#通过softmax函数，得到输出层每个神经元数值(概率)
         self.loss=-T.mean(T.log(prey)[T.arange(outdata.shape[0]),outdata])#损失函数
         self.para=[self.w,self.b]
         self.predict=T.argmax(prey,axis=1)
         self.error=T.mean(T.neq(T.argmax(prey,axis=1),outdata))




 #输入层到隐藏层
 class HiddenLayer:
     def __init__(self,inputx,nin,nout):
          a=np.sqrt(6./(nin+nout))
          ranmatrix=np.random.uniform(-a,a,(nin,nout));
          self.w=theano.shared(value=np.asarray(ranmatrix,dtype=theano.config.floatX),name='w')
          self.b=theano.shared(value=np.zeros((nout,),dtype=theano.config.floatX),name='b')
          self.out=T.tanh(T.dot(inputx,self.w)+self.b)
          self.para=[self.w,self.b]
 #传统三层感知器
 class mlp:
     def __init__(self,nin,nhid,nout):
         x=T.fmatrix('x')
         y=T.ivector('y')
         #前向
         hlayer=HiddenLayer(x,nin,nhid)
         olayer=softmax(hlayer.out,y,nhid,nout)
         #反向
         paras=hlayer.para+olayer.para
         dparas=T.grad(olayer.loss,paras)
         updates=[(para,para-0.1*dpara) for para,dpara in zip(paras,dparas)]
         self.trainfunction=theano.function(inputs=[x,y],outputs=olayer.loss,updates=updates)


     def train(self,trainx,trainy):
         return self.trainfunction(trainx,trainy)
 #卷积神经网络的每一层，包括卷积、池化、激活映射操作
 #img_shape为输入特征图，img_shape=（batch_size,特征图个数，图片宽、高）
 #filter_shape为卷积操作相关参数，filter_shape=（输入特征图个数、输出特征图个数、卷积核的宽、卷积核的高）
 #，这样总共filter的个数为：输入特征图个数*输出特征图个数*卷积核的宽*卷积核的高
 class LeNetConvPoolLayer:
     def __init__(self,inputx,img_shape,filter_shape,poolsize=(2,2)):
         #参数初始化
         assert img_shape[1]==filter_shape[1]
         a=np.sqrt(6./(filter_shape[0]+filter_shape[1]))

         v=np.random.uniform(low=-a,high=a,size=filter_shape)

         wvalue=np.asarray(v,dtype=theano.config.floatX)
         self.w=theano.shared(value=wvalue,name='w')
         bvalue=np.zeros((filter_shape[0],),dtype=theano.config.floatX)
         self.b=theano.shared(value=bvalue,name='b')

         covout=T.nnet.conv2d(inputx,self.w)#卷积操作

         covpool=T.signal.downsample.max_pool_2d(covout,poolsize)#池化操作

         self.out=T.tanh(covpool+self.b.dimshuffle('x', 0, 'x', 'x'))

         self.para=[self.w,self.b]



 #读取手写字体数据
 trainx,trainy=loadmnist()
 trainx=trainx.reshape(-1,1,28,28)
 batch_size=30
 m=trainx.shape[0]
 ne=m/batch_size



 batchx=T.tensor4(name='batchx',dtype=theano.config.floatX)#定义网络的输入x
 batchy=T.ivector('batchy')#定义输出y

 #第一层卷积层
 cov1_layer=LeNetConvPoolLayer(inputx=batchx,img_shape=(batch_size,1,28,28),filter_shape=(20,1,5,5))
 cov2_layer=LeNetConvPoolLayer(inputx=cov1_layer.out,img_shape=(batch_size,20,12,12),filter_shape=(50,20,5,5))#第二层卷积层
 cov2out=cov2_layer.out.flatten(2)#从卷积层到全连接层，把二维拉成一维向量
 hlayer=HiddenLayer(cov2out,4*4*50,500)#隐藏层
 olayer=softmax(hlayer.out,batchy,500,10)#

 paras=cov1_layer.para+cov2_layer.para+hlayer.para+olayer.para#网络的所有参数，把它们写在同一个列表里
 dparas=T.grad(olayer.loss,paras)#损失函数，梯度求导
 updates=[(para,para-0.1*dpara) for para,dpara in zip(paras,dparas)]#梯度下降更新公式

 train_function=theano.function(inputs=[batchx,batchy],outputs=olayer.loss,updates=updates)#定义输出变量、输出变量
 test_function=theano.function(inputs=[batchx,batchy],outputs=[olayer.error,olayer.predict])

 testx,testy=loadmnist(True)
 testx=testx.reshape(-1,1,28,28)

 train_history=[]
 test_history=[]

 for it in range(20):
     sum=0
     for i in range(ne):
         a=trainx[i*batch_size:(i+1)*batch_size]
         loss_train=train_function(trainx[i*batch_size:(i+1)*batch_size],trainy[i*batch_size:(i+1)*batch_size])
         sum=sum+loss_train
     sum=sum/ne
     print 'train_loss:',sum
     test_error,predict=test_function(testx,testy)
     print 'test_error:',test_error

     train_history=train_history+[sum]
     test_history=test_history+[test_error]
 n=len(train_history)
 fig1=plt.subplot(111)
 fig1.set_ylim(0.001,0.2)
 fig1.plot(np.arange(n),train_history,'-')

参考文献：

1、http://deeplearning.net/software/theano/tutorial/index.html#tutorial

*************作者：hjimce     联系qq：1393852684   更多资源请关注我的博客：http://blog.csdn.net/hjimce                原创文章，转载请保留本行信息*********************