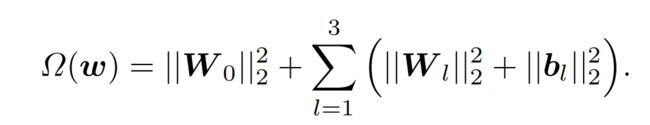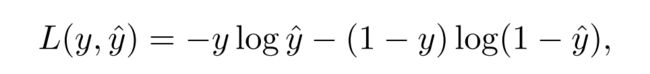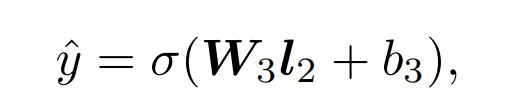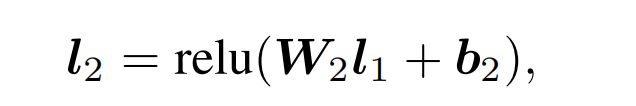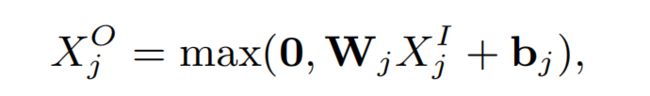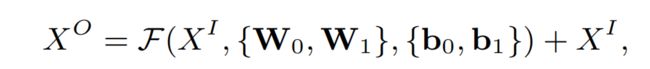CTR预估之DNN系列模型:FNN/PNN/DeepCrossing
前言
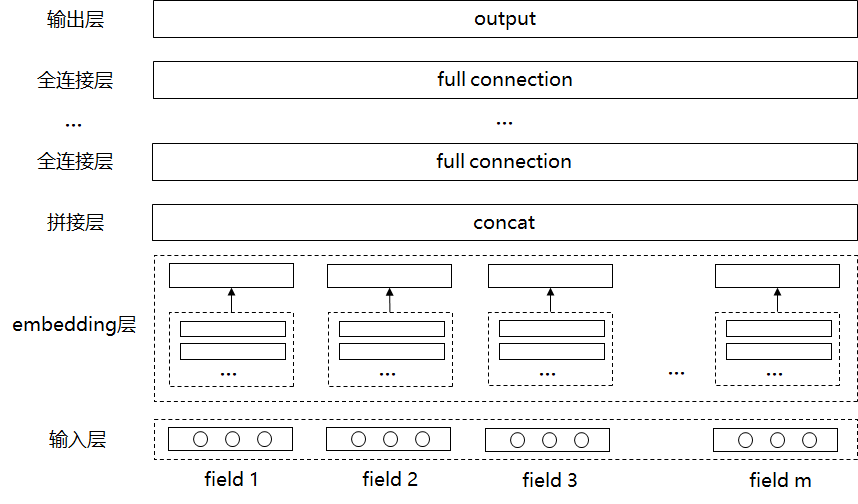
在上一篇文章中 CTR预估之FMs系列模型:FM/FFM/FwFM/FEFM,介绍了FMs系列模型的发展过程,开启了CTR预估系列篇章的学习。FMs模型是由线性项和二阶交互特征组成,虽然有自动学习二阶特征组合的能力,一定程度上避免了人工组合特征的问题,但却缺少高阶的特征组合,这篇文章的主题则是介绍deep neural networks (DNNs)下的ctr模型,能够自动学习高阶特征组合模式。如下图为最基础的DNN框架。
FNN
论文:Deep Learning over Multi-field Categorical Data: A Case Study on User Response Prediction
地址:https://arxiv.org/pdf/1601.02376.pdf
论文指出对于特征交互的自动学习,FMs模型是通过内积的方法,Gradient boosting trees则是通过生成树的方式。这些模型无法用到所有的特征组合可能,并且许多模型特征工程是人工设计,还有另外的问题是大部分ctr模型是浅层的结构,大部分是显式的学习模式,限制了隐式模式的建模能力,影响了模型的泛化能力,由此,论文提出了Factorisation-machine supported Neural Networks(FNN)模型。
模型结构
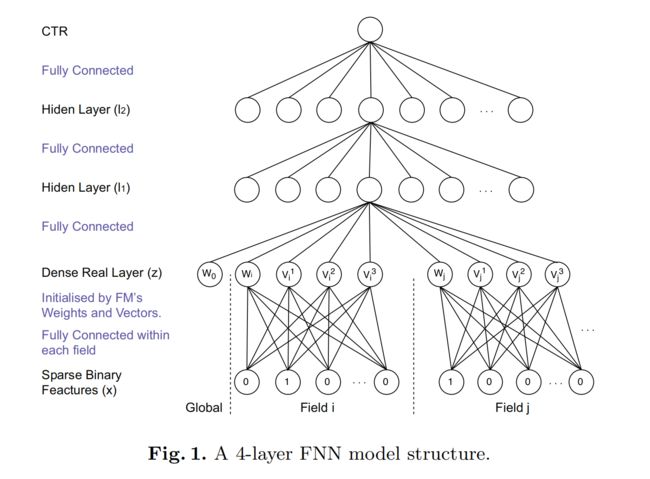
FNN的结构如上图所示,首先老生常谈地介绍下one-hot编码用于类别特征输入,对于每个field,会有多个单位(units),对应该filed的每种具体的取值feature,并且只会存在一个正单位(positive unit)赋值为1,其他都为负的,赋值为0,比如city=Landon,见上图中Sparse Binary Features(x)。下面我们从上往下一步步进行拆解学习FNN模型。
1. 最顶层是模型的输出。 预测的点击率 y ^ ∈ ( 0 , 1 ) \hat{y}\in (0,1) y^∈(0,1)。例如在特定的上下文场景下,特定的点击一个广告的概率:
y ^ = s i g m o i d ( W 3 l 2 + b 3 ) \hat{y}=sigmoid(W_3l_2+b_3) y^=sigmoid(W3l2+b3)
其中 s i g m o i d ( x ) = 1 / ( 1 + e − x ) sigmoid(x)=1/(1+e^{-x}) sigmoid(x)=1/(1+e−x), W 3 ∈ R 1 × L , b 3 ∈ R , l 2 ∈ R L 。 l 2 W_3\in \mathbb{R}^{1\times L},b_3\in \mathbb{R},l_2\in \mathbb{R}^L。l_2 W3∈R1×L,b3∈R,l2∈RL。l2便是该层网络的输入
2. 第2层隐藏层 l 2 l_2 l2的计算。 l 2 = t a n h ( W 2 l 1 + b 2 ) l_2=tanh(W_2l_1+b_2) l2=tanh(W2l1+b2)
其中, t a n h ( x ) = ( 1 − e − 2 x ) / ( 1 + e − 2 x ) , W 2 ∈ R L × M , b 2 ∈ R L , l 1 ∈ R M tanh(x)=(1-e^{-2x})/(1+e^{-2x}),W_2\in \mathbb{R}^{L\times M},b_2\in \mathbb{R}^L,l_1\in \mathbb{R}^M tanh(x)=(1−e−2x)/(1+e−2x),W2∈RL×M,b2∈RL,l1∈RM。论文实验 t a n h ( ⋅ ) tanh(\cdot) tanh(⋅)比其他的激活函数表现更好。
3. 第1层隐藏层 l 1 l_1 l1的计算。 l 1 = t a n h ( W 1 z + b 1 ) l_1=tanh(W_1z+b_1) l1=tanh(W1z+b1)
其中, W 1 ∈ R M × J , b 1 ∈ R M , z ∈ R J W_1\in \mathbb{R}^{M\times J},b_1\in \mathbb{R}^M,z\in \mathbb{R}^J W1∈RM×J,b1∈RM,z∈RJ。
4. Dense Real Layer(z)。 z = ( w 0 , z 1 , z 2 , . . . , z i , . . . , z n ) z=(w_0,z_1,z_2,...,z_i,...,z_n) z=(w0,z1,z2,...,zi,...,zn)
其中, w 0 w_0 w0是一个全局标量参数,n是fields的数目。 z i ∈ R K + 1 z_i\in \mathbb{R}^{K+1} zi∈RK+1
5. Initialised by FM’s Weights and Vectors。 z i = W 0 i ⋅ x [ s t a r t i : e n d i ] = ( w i , v i 1 , v i 2 , . . . , v i K ) z_i=W^i_0\cdot x[start_i:end_i]=(w_i,v^1_i,v^2_i,...,v^K_i) zi=W0i⋅x[starti:endi]=(wi,vi1,vi2,...,viK)
其中, s t a r t i 和 e n d i start_i和end_i starti和endi是第i个field的feature索引起点和终点, W 0 i ∈ R ( K + 1 ) × ( e n d i − s t a r t i + 1 ) W^i_0\in \mathbb{R}^{(K+1)\times (end_i-start_i+1)} W0i∈R(K+1)×(endi−starti+1)。即** z i z_i zi由一个偏置项 w i w_i wi和向量 v i v_i vi组成,分别对应FMs中第i个filed的权重和对应取值feature的隐向量embedding,是由经过预训练的FMs模型加载初始化 [ 1 ] ^{[1]} [1],使用了公开数据集进行训练得到泛化性的FMs向量embeddings。**
6. pre-training。 除了上述提到Dense Real Layer的参数z是由FMs预训练得到,FNN模型上层网络的参数也是使用contrastive divergence [ 2 ] ^{[2]} [2]进行RBM(restricted Boltzmann machine)预训练 [ 3 ] ^{[3]} [3],细节详见 [ 4 , 5 ] ^{[4,5]} [4,5]。
7. ctr微调。 使用交叉熵进行最小化训练: L ( y , y ^ ) = − y l o g ( y ^ ) − ( 1 − y ) l o g ( 1 − y ^ ) L(y,\hat{y})=-ylog(\hat{y})-(1-y)log(1-\hat{y}) L(y,y^)=−ylog(y^)−(1−y)log(1−y^),y为真实标签0/1,代表是否点击。
总体来看,FNN其实是一个最基础的通用CTR深度神经网络框架,one-hot编码的输入,经过embedding layer层(特征embedding类似于上图[FNN结构]FMs的权重+向量),然后通过多个DNN全连接层,最后通过sigmoid函数得到预测的点击概率。
SNN
论文还提出了另外一个模型Sampling-based Neural Networks(SNN),与FNN的不同之处只是底层网络的结构和训练方法不同。SNN的底层网络是一个带sigmoid激活函数的全连接网络,而不是从FMs加载的向量:
为了初始化这部分的权重参数,论文使用了restricted Boltzmann machine (RBM) [ 6 ] ^{[6]} [6]和denoising auto-encoder (DAE) [ 7 ] ^{[7]} [7]两种预训练方法,这里的RBM训练方法与上述FNN中的一样是使用contrastive divergence,而DAE则是使用非监督的SGD方法,如下图:
其实RBM和DAE的训练思路大致都是通过投影(Projection) ->重构来学习参数,训练目标是让重构前后的向量空间尽量靠近。
这里再来理解下论文提出的采样(sampling-based)预训练方法:
- 对于每个训练实例中的每个field,比如city,只会存在一个正值的feature,比如city=London;
- 此时,不是对整个特征集进行建模,而是随机采样m个非正值feature(negative units)并将它们置为0,比如当m=1时,采样了city=Paris这个negative units,这些正值feature和negative units的feature则分别对应上图[SNN结构及预训练]-(b)和©中的白色单元1和0;
- 而其他未被采样到的negative units则会忽略,不作为输入,对应其中的黑色单元。
L2正则化
实验使用了 iPinYou数据集,第一列为广告主的数量。
论文中提及的参考文献:
- Rendle, S.: Factorization machines with libfm. ACM TIST 3(3), 57 (2012)
- Hinton, G.E.: Training products of experts by minimizing contrastive divergence. Neural computation 14(8), 1771–1800 (2002)
- Bengio, Y., Lamblin, P., Popovici, D., Larochelle, H., et al.: Greedy layer-wise training of deep networks. NIPS 19, 153 (2007)
- Hinton, G.: A practical guide to training restricted boltzmann machines. Momentum 9(1), 926 (2010)
- Hinton, G.E., Salakhutdinov, R.R.: Reducing the dimensionality of data with neural networks. Science 313(5786), 504–507 (2006)
- Hinton, G.: A practical guide to training restricted boltzmann machines. Momentum 9(1), 926 (2010)
- Bengio, Y., Yao, L., Alain, G., Vincent, P.: Generalized denoising auto-encoders as generative models. In: NIPS. pp. 899–907 (2013)
PNN
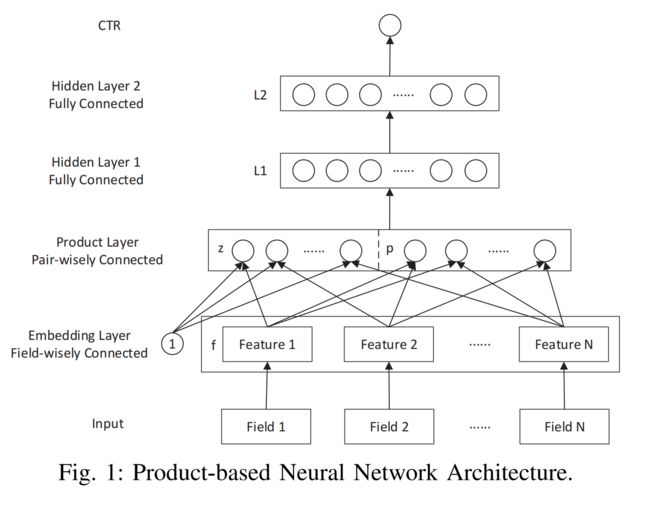
论文:Product-based Neural Networks for User Response Prediction
地址:https://arxiv.org/pdf/1611.00144.pdf
论文认为FNN中embeddings初始化的质量存在很大局限,大大取决于FMs模型。更重要的是,FNN中的feature embeddings到MLP全连接层是“加法”(add)操作,在这种multi-fields的类别数据上交互效果可能不如“乘积”(product)操作,提出了Product-based Neural Network(PNN):
- embeddings的初始化不通过FMs预训练;
- 特征向量使用product layer来对特征交互进行建模;
- 通过全连接MLPs更深入的提炼高阶特征模式
模型结构
PNN模型的结构如上图,其中Hidden Layer1-Fully Connected -> Hidden Layer2-Fully Connected -> CTR这三个部分与FNN模型基本上是相同,就是普通的全连接网络层,唯一不同的是隐藏层1和2使用的relu激活函数,而不是tanh:
而于FNN模型的最大区别,也是PNN模型的创新之处就在于Hidden Layer1的输入是由product layer的乘积操作得到: l 1 = r e l u ( l z + l p + b 1 ) l_1=relu(l_z+l_p+b_1) l1=relu(lz+lp+b1)。
首先,定义内积(tensor inner product)公式,并得到 l z 、 l p l_z、l_p lz、lp: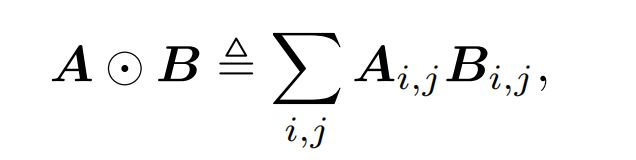

其中 W z n , W p n W_z^n,W_p^n Wzn,Wpn是product layer的权重,维度自然分别于z和p相同; D 1 D_1 D1为第一层隐藏层的维度。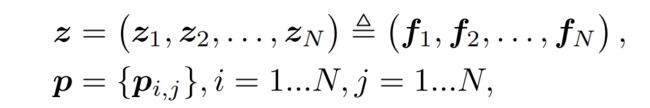
f i ∈ R M f_i\in \mathbb{R}^M fi∈RM是第i个field的embedding vector: f i = W 0 i x [ s t a r t i : e n d i ] f_i=W^i_0x[start_i:end_i] fi=W0ix[starti:endi],即对应取值的feature的向量,这里与FNN模型是一样的,只是没有加入第i个field的权重。
p i , j = g ( f i , f j ) p_{i,j}=g(f_i,f_j) pi,j=g(fi,fj),论文设计了两种不同的操作g,对应两种PNN变体:IPNN和OPNN。
IPNN
首先介绍第一种: Inner Product-based Neural Network(IPNN),这里的向量内积操作为: p i , j = g ( f i , f i ) = < f i , f j > , p ∈ R N × N p_{i,j}=g(f_i,f_i)=
l z n = W z n ⊙ z = ∑ 1 N ∑ 1 M ( W z n ) i , j z i , j l_z^n=W^n_z\odot z=\sum^N_1\sum^M_1(W_z^n)_{i,j}z_{i,j} lzn=Wzn⊙z=∑1N∑1M(Wzn)i,jzi,j
l p n = W p n ⊙ p = ∑ 1 N ∑ 1 N ( W p n ) i , j p i , j l_p^n=W^n_p\odot p=\sum^N_1\sum^N_1(W_p^n)_{i,j}p_{i,j} lpn=Wpn⊙p=1∑N1∑N(Wpn)i,jpi,j
可以算出 l 1 l_1 l1的空间复杂度为 O ( D 1 N ( M + N ) ) O(D_1N(M+N)) O(D1N(M+N)),时间复杂度为 O ( N 2 ( D 1 + M ) ) O(N^2(D_1+M)) O(N2(D1+M)), D 1 D_1 D1是Hidden Layer1的输入的size,M是embeddings的size,都属于模型的超参数,N则是field的数量。
一阶分解。 受到FM的启发,论文使用矩阵因子分解的方法,令 W p n = θ n θ n T , θ ∈ R N W_p^n=\theta^n\theta^{nT},\theta\in \mathbb{R}^N Wpn=θnθnT,θ∈RN,将 l 1 l_1 l1的计算简化为如下: 其中, δ i n ∈ R M \delta_i^n\in \mathbb{R}^M δin∈RM代表特征向量乘上一个权重: δ i n = θ i n f i , δ n = ( δ 1 n , δ 2 n , . . . , δ i n , . . . , δ N n ) ∈ R N × M \delta_i^n=\theta_i^nf_i,\delta^n=(\delta^n_1,\delta^n_2,...,\delta^n_i,...,\delta^n_N)\in \mathbb{R}^{N\times M} δin=θinfi,δn=(δ1n,δ2n,...,δin,...,δNn)∈RN×M。
其中, δ i n ∈ R M \delta_i^n\in \mathbb{R}^M δin∈RM代表特征向量乘上一个权重: δ i n = θ i n f i , δ n = ( δ 1 n , δ 2 n , . . . , δ i n , . . . , δ N n ) ∈ R N × M \delta_i^n=\theta_i^nf_i,\delta^n=(\delta^n_1,\delta^n_2,...,\delta^n_i,...,\delta^n_N)\in \mathbb{R}^{N\times M} δin=θinfi,δn=(δ1n,δ2n,...,δin,...,δNn)∈RN×M。
随着第n个node的一阶分解, l p l_p lp最终的公式如下,空间和时间复杂度 都降到了 O ( D 1 M N ) O(D_1MN) O(D1MN):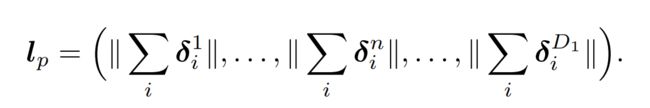
其中, δ n i ∈ R K \delta^i_n\in \mathbb{R}^K δni∈RK,K阶分解表现更好,但也会带来K倍的计算度。
OPNN
第二种则为Outer Product-based Neural Network(OPNN),与IPNN唯一不同的只是p的内积方式,OPNN使用的内积操作是: g ( f i , f i ) = f i f j T g(f_i,f_i)=f_if_j^T g(fi,fi)=fifjT,因此对于p的每个元素是一个矩阵: p i , j ∈ R M × M p_{i,j}\in \mathbb{R}^{M\times M} pi,j∈RM×M。 l 1 l_1 l1的时间复杂度和空间复杂度都变为了 O ( D 1 M 2 N 2 ) O(D_1M^2N^2) O(D1M2N2)。
为了降低复杂度,论文使用了superposition(叠加)的方法,重新定义了p的计算: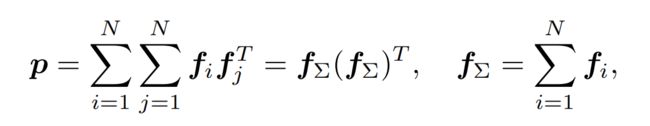
通过简化p的计算 p ∈ R M × M p\in \mathbb{R}^{M\times M} p∈RM×M,对应的 W p ∈ R D 1 × M × M W_p\in \mathbb{R}^{D_1\times M\times M} Wp∈RD1×M×M, l 1 l_1 l1的空间和时间复杂度都降低为 O ( D 1 M ( M + N ) ) O(D_1M(M+N)) O(D1M(M+N))
KPNN & PIN
论文:Product-based Neural Networks for User Response Prediction over Multi-field Categorical Data
地址:https://arxiv.org/pdf/1807.00311.pdf
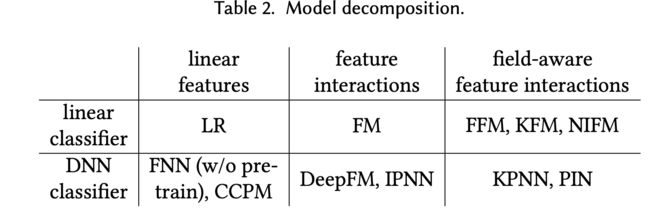
原团队作者在后来又发表了一篇PNN的论文,去掉了上述针对复杂度的公式优化,使用FMs的特征对交互操作,提出了不同框架形式的PNN,包括下图中的三种PNN:
并且统一了PNN的一般框架,由特征向量(embeddings)、特征向量的交互(product)、embeddings和product拼接后输入DNN:

再结合上图[新PNN结构图]和图[PNN组合],可以看出,新提出的PNN其实就是使用不同的feature extractors,即使用不同的特征向量交互(product)操作。
Inner Product-based Neural Network(IPNN). 这里的product操作其实就完全跟FMs模型一样,使用内积的操作。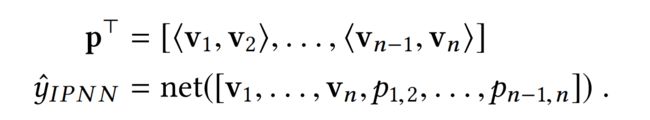
Kernel Product-based Neural Network(KPNN). KPNN使用的product操作则包括两种:FFM、FM的扩展-FM+linear kernel。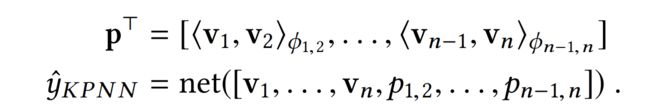
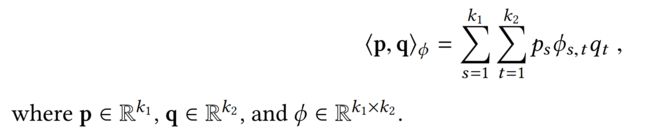
Product-network In Network (PIN). PIN使用的product操作则是FM的另外一种扩展形式:FM+micro network kernel。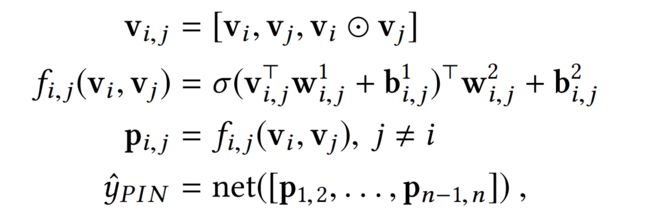
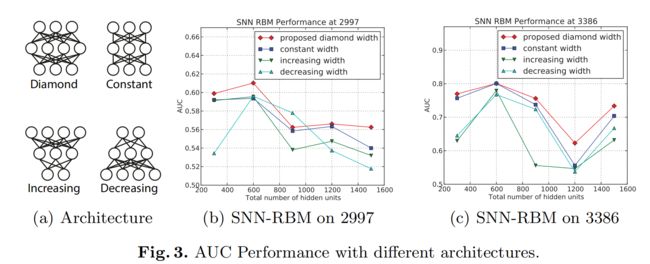
实验结果
- IPNN和OPNN与FM对比效果更优,且收敛更快;
- 使用IPNN和OPNN拼接的product layer,相比单独的product layer效果反而下降。
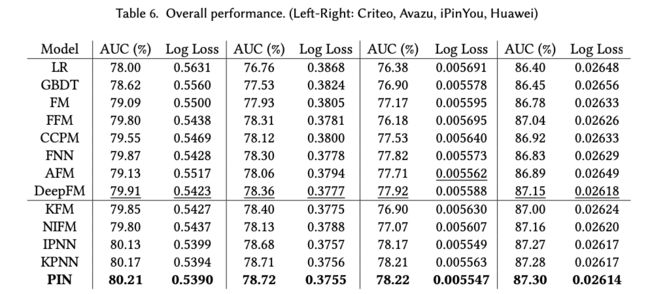
KPNN和PIN的效果对比如下图:
Deep Crossing
论文:Deep Crossing - Web-Scale Modeling without Manually Crafted Combinatorial Features
地址:https://www.kdd.org/kdd2016/papers/files/adf0975-shanA.pdf
虽然这篇论文是在解决用户在搜索场景下的广告点击问题,但其实这本质还是与推荐系统的ctr任务一样的,item对应广告。论文尝试使用残差网络来替代普通的DNN网络,其他与基础的ctr-DNN框架基本一致,Deep Crossing的网络框架如下图:
Embedding and Stacking Layers
- 首先,还是常规的特征进行one-hot编码,然后进行embeddings映射,以此来大大减少one-hot向量的维度。不过论文对embeddings加入了bias,并且使用了非线性变换ReLU;
- 接着不同输入的embeddings进行拼接,即stacked (concatenated)
Residual Layers
残差网络的优点在于能够缓解梯度消失,可以使用更深的网络层数,建模更高阶的特征,增强模型的表达能力。
总结
本文介绍的三种ctr模型框架的出发点都是为了解决人工构造组合特征的问题,并且希望加入深层网络(DNN)来隐式挖掘高阶特征:
- PNN与基础的DNN网络框架一致,只是embeddings是从FM模型预训练进行加载;
- FNN则是保留特征product这样的显式建模,与embeddings拼接输入到DNN,并且提出多种product操作;
- Deep Crossing则是用残差网络来代替DNN。
代码实现:GitHub仓库