python数据分析与挖掘实战—第5章(挖掘建模)(1)
经过数据探索与数据预处理,得到了可以直接建模的数据。根据数据挖掘目标和数据形式: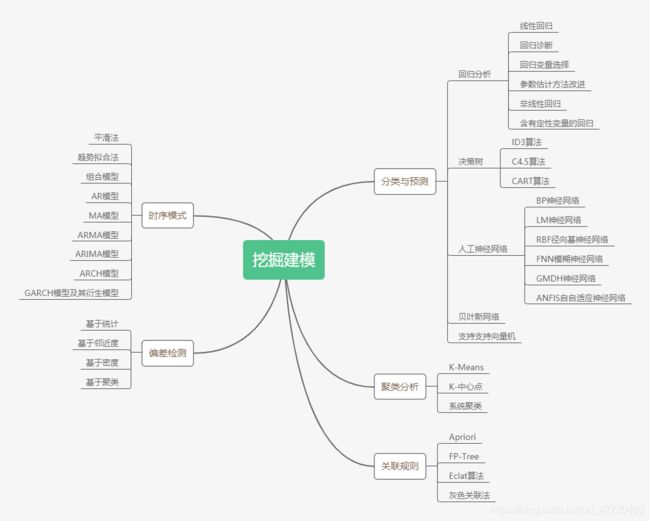
5.1 分类与预测
- 分类:预测分类标号(离散属性),构造一个分类模型,输入样本的属性值,输出对应的类别,将每个样本映射到预先定义好的类别。分类模型建立在已有类标记的数据集上,模型在已有样本上的准确率可以方便计算,所以分类属于有监督的学习。
- 预测:建立连续值函数模型,预测给定自变量对应的因变量的值,建立两种或两种以上变量间相互依赖的函数模型,然后进行预测或控制。
5.1.1 实现过程
分类算法:
第一步:学习步
通过归纳分析训练样本集来建立分类模型得到分类规则
第二步:分类步
先用已知的测试样本集评估分类规则的准确率,如果准确率可以接受,则使用该模型对未知类标号的待测样本集进行预测

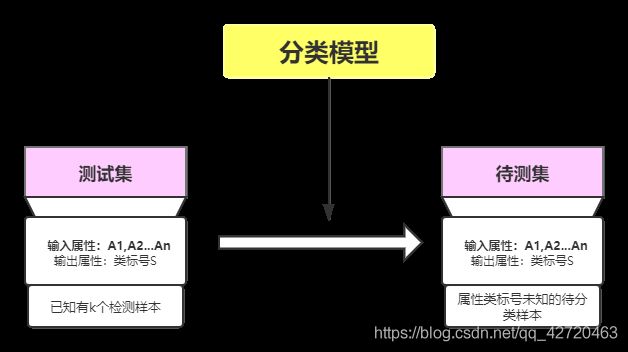
预测算法:
第一步:通过训练集建立预测属性(数值型的)的函数模型
第二步:在模型通过检验后进行预测或控制
5.1.2 常用的分类与预测算法
| 算法名称 | 算法描述 |
|---|---|
| 回归分析 | 确定预测属性(数值型)与其他变量间相互依赖的定量关系最常用的统计学方法 |
| 决策树 | 采用自顶向下的递归方法,在内部节点进行属性值的比较,并根据不同的属性值从该节点向下分支,最终得到的叶节点是学习划分的类 |
| 人工神经网络 | 模仿大脑神经网络结构和功能而建立的信息处理系统,表示神经网络的输入与输出变量之间关系的模型 |
| 贝叶斯网络 | 又称信度网络,是Bayes方法的扩展,是目前不确定知识表达和推理领域最有效的理论模型之一 |
| 支持向量机 | 通过某种非线性映射,把低维的非线性可分转化为高维的线性可分,在高维空间进行线性分析的算法 |
5.1.3 回归分析
回归分析是通过建立模型来研究变量之间相互关系的密切程度、结构状态及进行模型预测的一种有效工具。按照研究方法划分,回归分析研究的范围大致如下:

常用的回归模型如下表:
| 回归模型名称 | 适用条件 | 算法描述 |
|---|---|---|
| 线性回归 | 因变量与自变量是线性关系 | 对一个或多个自变量和因变量之间的线性关系进行建模,可用最小二乘法求解模型系数 |
| 非线性回归 | 因变量与自变量之间不都是线性关系 | 对一个或多个自变量和因变量之间的非线性关系进行建模。如果非线性关系可以通过简单的函数变换转化成线性关系,用线性回归的思想求解;如果不能转化,用非线性最小二乘法求解 |
| Logistic回归 | 因变量一般有1和0(是否)两种取值 | 是广义线性回归的特例,利用Logistic函数将因变量的取值范围控制在0和1之间,表示取值为1的概率 |
| 岭回归 | 参与建模的自变量直接具有多重共线性 | 是一种改进最小二乘估计的方法 |
| 主成分回归 | 参与建模的自变量直接具有多重共线性 | 根据主成分分析的思想提出来的,是对最小二乘法的一种改进,它是参数估计的一种有偏估计,可以消除自变量之间的多重共线性 |
(1)Logistic函数
Logistic回归模型中的因变量只有1-0(如是和否、发生和不发生)两种取值。假设在p个独立自变量x1,x2,…,xp作用下,记
- y取1的概率是p = P(y = 1|X)
- 取0概率是1-p
- 取1和0的概率之比为 p 1 − p \frac{p}{1-p} 1−pp,称为事件的优势比(odds)
- 对odds取自然对数即得: Logistic变换Logit( p) = ln( p 1 − p \frac{p}{1-p} 1−pp)
- 令其等于z,则p = 1 1 + e − z \frac{1}{1+e^{-z}} 1+e−z1即位Logistic函数,如图所示:
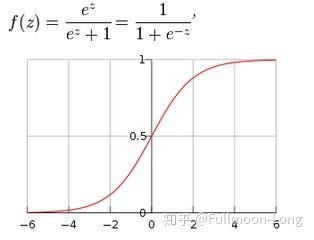
当p在(0,1)之间变化时,odds的取值范围是(0,+∞),则ln( p 1 − p \frac{p}{1-p} 1−pp)的取值范围是(-∞,+∞),即自变量可在任意范围内取值。
(2)Logistic回归模型
Logistic回归模型是建立ln( p 1 − p \frac{p}{1-p} 1−pp)与自变量的线性回归模型
Logistic回归模型为:
记 g ( x ) = β 0 + β 1 x 1 + . . . + β p x p + ε g(x)=\beta _{0}+\beta _{1}x_{1}+...+\beta _{p}x_{p}+\varepsilon g(x)=β0+β1x1+...+βpxp+ε,得到:
(3)Logistic回归模型解释
- β 0 \beta_{0} β0:在没有自变量,即x1,x2,…,xp全部取0,y=1与y=0发生概率之比的自然对数
- β 1 \beta_{1} β1:在某自变量xi变化时,即xi=1与xi=0相比,y=1优势比的对数值
2.建模步骤

x = data.iloc[:,:8].values #选取年龄-其他负债列
y = data.iloc[:,8].values #违约列
data.head() #见下图
from sklearn.linear_model import LogisticRegression as LR
from stability_selection import RandomizedLogisticRegression as RLR
rlr = RLR() #建立随机逻辑回归模型,筛选变量
rlr.fit(x, y) #训练模型
rlr.get_support() #获取特征筛选结果,也可以通过scores_方法获取各个特征的分数
#筛选好特征
x = data[data.columns[[2,3,5,6]]] #工龄、地址、负债率、信用卡负债
lr = LR()
lr.fit(x, y)
print('模型的平均正确率为:%s' % lr.score(x, y))
输出结果:
模型的平均正确率为:0.8142857142857143
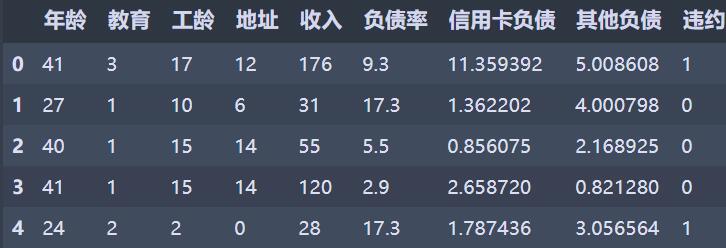
get_support()报错,书上筛选变量为工龄、地址、负债率、信用卡负债,以此建立逻辑回归模型。
5.1.4 决策树
决策树是一树状结构,它的每一个叶节点对应着一个分类,非叶节点对应着在某个属性上的划分,根据样本在该属性上的不同取值将其划分成若干个子集。对于非纯的叶节点,多数类的标号给出达到这个节点的样本所属的类。构造决策树的核心问题是在每一步如何选择适当的属性对样本做拆分。
| 决策树算法 | 算法描述 |
|---|---|
| ID3算法 | 其核心是在决策树的各级节点上,使用信息增益方法作为属性的选择标准,来帮助确定生成每个节点所应采用的合适属性,只适用于离散的描述属性 |
| C4.5算法 | C4.5决策树生成算法相对于ID3算法的重要改进是使用信息增益率来选择节点属性。可以克服ID3算法的不足,既能处理离散的描述属性,也可以处理连续的描述属性 |
| CART算法 | 非参数分类和回归方法,通过构建树、修剪树、评估树来构建一个二叉树。当终结点是连续变量时,该树为回归树;当终结点是分类变量,该树为分类树 |
1.ID3算法简介及基本原理
- 基于信息熵来选择最佳测试属性,选择当前样本集中具有最大信息增益值的属性作为测试属性。
- 样本集的划分依据测试属性的取值进行,测试属性有多少不同取值就将样本集划分为多少个样本集,同时决策树上相应于该样本集的节点长出新的叶子节点。
- 根据信息论理论,采用划分后样本集的不确定性作为衡量划分好坏的标准,用信息增益值度量不确定性:信息增益值越大,不确定性越小。
设S是s个数据样本的集合。假定类别属性具有m个不同的值, C i C_{i} Ci(i=1,2,3,…,m)。设 s i s_{i} si是类 C i C_{i} Ci中的样本数。对一个给定的样本,它总的信息熵为:
其中, P i P_{i} Pi是任意样本属于 C i C_{i} Ci的概率,一般用 s i s \frac{s_{i}}{s} ssi估计。
2.ID3算法具体流程(例子,具体步骤省略)
- 对当前样本集合,计算所有属性的信息增益
Gain(天气) = I(18,16) - E(天气) = 0.997503 - 0.957043 = 0.04046
Gain(是否周末)= I(18,16) - E(是否周末) = 0.997503 - 0.858109 = 0.139394
Gain(是否有促销) = I(18,16) - E(是否有促销) = 0.997503 - 0.870235 = 0.127268
其中,I(18,16)表示总的信息熵,数据中总记录数为34,而销售数量为“高”的数据有18,“低”的有16。 - 选择信息增益最大的属性作为测试属性,把测试属性取值相同的样本划为同一个子样本集
是否为周末的信息增益值最大,它的两个属性值“是”和“否”作为该根结点的两个分支。然后继续对该根节点的3个分支进行节点的划分,针对每一个分支点继续进行信息增益的计算,如此循环反复,直到没有新的节点分支,最终构成一棵决策树。生成的决策树模型如下:
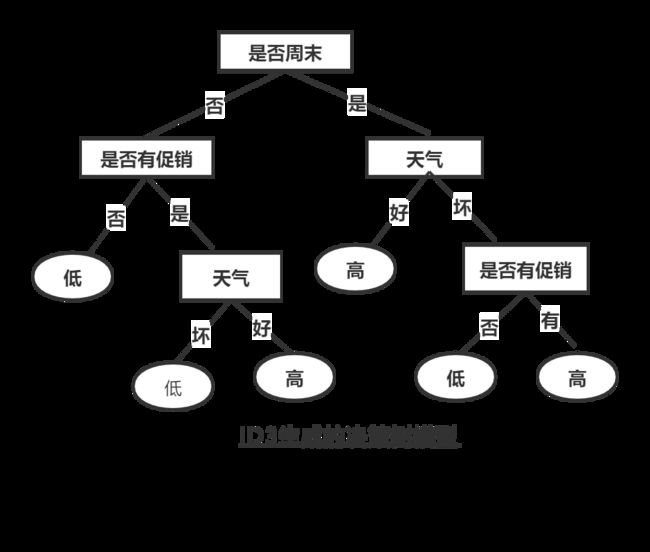
- 若子样本集的类别属性只含有单个属性,则分支为叶子节点,判断其属性值并标上相应的符号,然后返回调用处;否则对子样本集递归调用本算法
从上面的决策树模型可以看出门店的销售高低和各个属性之间的关系,并可以提取以下决策规则。
- 若周末属性为“是”,天气为“好”,则销售数量为“高”
- 若周末属性为“是”,天气为“坏”,促销属性为“是”,则销售数量为“高“
- 若周末属性为”是“,天气为”坏”,促销属性为“否”,则销售属性为“低”
- 若周末属性为“否”,促销属性为“否”,则销售数量为“低”
- 若周末属性为“否”,促销属性为“是”,天气为“好”,则销售数量为“高”
- 若周末属性为“否”,促销属性为“是”,天气为“坏”,则销售数量为“低”
3. 局限:
ID3决策树采用信息增益作为选择测试属性的标准,会偏向于选择取值较多的,即所谓高度分支属性,而这类属性不一定是最优的属性。同时ID3决策树算法只能处理离散属性,对于连续型的属性,在分类前需要对其进行离散化。
4. 代码实现:
#决策树算法预测销量高低
import pandas as pd
filename = 'G:/Python数据分析与挖掘实战/chapter5/demo/data/sales_data.xls'
data = pd.read_excel(filename, index_col='序号') #导入数据
#数据是类别标签,要将它转换为数据
#用1来表示“好”,“是”,“高”这三个属性,用-1表示相反
data[data == "好"] = 1
data[data == "是"] = 1
data[data == "高"] = 1
data[data != 1] = -1
x = data.iloc[:,:3].astype(int)
y = data.iloc[:,3].astype(int)
from sklearn.tree import DecisionTreeClassifier as DTC
dtc = DTC(criterion='entropy') #建立决策树模型,基于信息熵
dtc.fit(x, y) #训练模型
#导入相关函数,可视化决策树
#导出的结果是一个dot文件,需要安装Graphviz才能将它转换为pdf或png等格式
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
with open("Tree.dot", 'w') as f:
f = export_graphviz(dtc, feature_names = x.columns, out_file = f)
运行代码后,将会输出一个tree.dot的文本文件,由于我们输出中包含中文,需要用文本编辑器在文件指定中文字体,如,

然后将它保存为UTF-8格式,为了进一步将它转换为可视化格式,需要安装Graphviz,然后在命令行中以如下方式编译
![]()
生成的结果图如下: