8.1 正弦波振荡电路(1)
正弦波振荡电路是在没有外加输入信号的情况下,依靠电路自激振荡而产生正弦波输出电压的电路。它广泛地应用于测量、遥控、通讯、自动控制、热处理和超声波电焊等加工设备之中,也作为模拟电子电路的测试信号。
一、概述、
1、产生正弦波振荡的条件
在负反馈放大电路的稳定性一节知道,倘若在低频段或高频段中存在频率 f 0 f_0 f0,使电路产生的附加相移为 ± π ±\,π ±π,而且当 f = f 0 f=f_0 f=f0 时 ∣ A ˙ F ˙ ∣ > 1 |\dot A\dot F|>1 ∣A˙F˙∣>1,则电路将产生自激振荡。振荡频率除了决定于电路中的电阻和电容外,还决定于晶体管的极间电容、电路的分布电容等人们不能确定的因素。
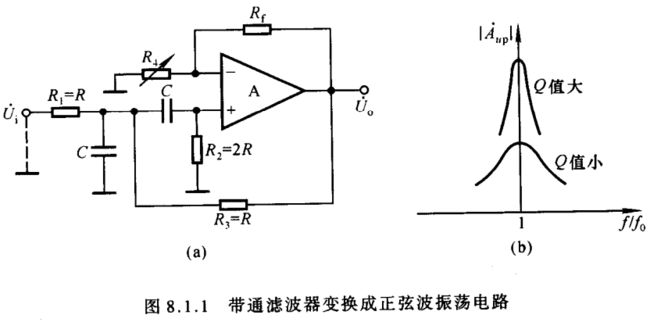
根据7.3.3节有源滤波器中带通滤波电路的分析,图8.1.1(a)所示带通滤波器中同相比例运算电路的比例系数 A ˙ u f \dot A_{uf} A˙uf、电路的品质因数 Q Q Q、中心频率 f 0 f_0 f0、 f = f 0 f=f_0 f=f0 时的放大倍数(即通带放大倍数) A ˙ u p \dot A_{up} A˙up、截止频率 f p 1 f_{p1} fp1 与 f p 2 f_{p2} fp2 分别为 A ˙ u f = U ˙ o U ˙ p = 1 + R f R 4 \dot A_{uf}=\frac{\dot U_o}{\dot U_p}=1+\frac{R_f}{R_4} A˙uf=U˙pU˙o=1+R4Rf Q = ∣ 1 3 − A ˙ u f ∣ Q=\Big|\frac{1}{3-\dot A_{uf}}\Big| Q= 3−A˙uf1 f 0 = 1 2 π R C f_0=\frac{1}{2πRC} f0=2πRC1 A ˙ u p = A ˙ u f 3 − A ˙ u f = Q A ˙ u f \dot A_{up}=\frac{\dot A_{uf}}{3-\dot A_{uf}}=Q\dot A_{uf} A˙up=3−A˙ufA˙uf=QA˙uf { f p 1 = f 0 2 [ ( 3 − A ˙ u f ) 2 + 4 − ( 3 − A ˙ u f ) ] f p 2 = f 0 2 [ ( 3 − A ˙ u f ) 2 + 4 + ( 3 − A ˙ u f ) ] \left\{\begin{matrix}f_{p1}=\displaystyle\frac{f_0}{2}[\sqrt{(3-\dot A_{uf})^2+4}-(3-\dot A_{uf})]\\f_{p2}=\displaystyle\frac{f_0}{2}[\sqrt{(3-\dot A_{uf})^2+4}+(3-\dot A_{uf})]\end{matrix}\right. ⎩ ⎨ ⎧fp1=2f0[(3−A˙uf)2+4−(3−A˙uf)]fp2=2f0[(3−A˙uf)2+4+(3−A˙uf)]从以上表达式可以看出,当 R 4 R_4 R4 减小时, A ˙ u f \dot A_{uf} A˙uf 增大, Q Q Q 值增大( A ˙ u f < 3 \dot A_{uf}<3 A˙uf<3 ), A ˙ u p \dot A_{up} A˙up 必将随之增大;而且 f p 1 f_{p1} fp1 与 f p 2 f_{p2} fp2 之差减小,即频带变窄。从图(b)所示的幅频特性可以看出, Q Q Q 值愈大,选频特性愈好。可知,当 A ˙ u f \dot A_{uf} A˙uf 趋近于 3 时, A ˙ u p \dot A_{up} A˙up 趋近于无穷大,表明电路即使在无输入的情况下,也会有频率为 f 0 f_0 f0 的输出电压,即电路产生了自激振荡。因为电路仅对频率为 f 0 f_0 f0 的信号放大,而对其它频率的信号均迅速衰减为零,所以输出电压为 f = f 0 f=f_0 f=f0 的正弦波。输出电压是靠电阻 R 3 R_3 R3 反馈回来的信号取代输入信号来维持的。可见,带通滤波器在参数取值合适时可以变换成正弦波振荡电路,而且振荡频率为 f 0 f_0 f0。与负反馈放大电路的自激振荡不同,正弦波振荡电路的振荡频率是认为确定的。
综上所述,在正弦波振荡电路中,一要反馈信号能够取代输入信号,而若要如此,电路中必须引入正反馈;二要有外加的选频网络,用于确定振荡频率。
通常,可将正弦波振荡电路分解为图8.1.2(a)所示方框图,上一个方框为放大电路,下一个方框为反馈网络,反馈极性为正。当输入量为零时,反馈量等于净输入量,如图(b)所示。由于电扰动(如合闸通电),电路产生一个幅值很小的输出量,它含有丰富的频率,而如果电路只对频率为 f 0 f_0 f0 的正弦波产生正反馈过程,则输出信号

在正反馈过程中, X o X_o Xo 越来越大。由于晶体管的非线性特性,当 X o X_o Xo 的幅值增大到一定程度时,放大倍数的数值将减小。因此, X o X_o Xo 不会无限制地增大,当 X o X_o Xo 增大到一定数值时,电路达到动态平衡。这时,输出量通过反馈网络产生反馈量作为放大电路的输入量,而输入量又通过放大电路维持着输出量,写成表达式为 X ˙ o = A ˙ X ˙ f = A ˙ F ˙ X ˙ o \dot X_o=\dot A\dot X_f=\dot A\dot F\dot X_o X˙o=A˙X˙f=A˙F˙X˙o也就是说正弦波振荡的平衡条件为 A ˙ F ˙ = 1 ( 8.1.1 ) \dot A\dot F=1\kern 40pt(8.1.1) A˙F˙=1(8.1.1)写成模与相角的形式为 { ∣ A ˙ F ˙ ∣ = 1 ( 8.1.2 a ) φ A + φ F = 2 n π ( n 为整数 ) ( 8.1.2 b ) \left\{\begin{matrix}|\dot A\dot F|=1\kern 115pt(8.1.2a)\\\varphi_{\scriptscriptstyle A}+\varphi_{\scriptscriptstyle F}=2nπ\kern 20pt(n\,为整数)\kern 20pt(8.1.2b)\end{matrix}\right. {∣A˙F˙∣=1(8.1.2a)φA+φF=2nπ(n为整数)(8.1.2b)式(8.1.2a)称为幅值平衡条件,式(8.1.2b)称为相位平衡条件,分别简称为幅值条件和相位条件。为了使输出量在合闸后能够有一个从小到大直至平衡在一定幅值的过程,电路的起振条件为 ∣ A ˙ F ˙ ∣ > 1 ( 8.1.3 ) |\dot A\dot F|>1\kern 40pt(8.1.3) ∣A˙F˙∣>1(8.1.3)电路把除频率 f = f 0 f=f_0 f=f0 以外的输出量均逐渐衰减为零,因此输出量为 f = f 0 f=f_0 f=f0 的正弦波。
2、正弦波振荡电路的组成及分类
从以上分析可知,正弦波振荡电路必须由以下四部分组成:
(1)放大电路:保证电路能够有从起振到动态平衡的过程,使电路获得一定幅值的输出量,实现能量的控制。
(2)选频网络:确定电路的振荡频率,使电路产生单一频率的振荡,即保证电路产生正弦波振荡。
(3)正反馈网络:引入正反馈,使放大电路的输入信号等于反馈信号。
(4)稳幅环节:也就是非线性环节,作用是使输出信号幅值稳定。
在不少实用电路中,常将选频网络和正反馈网络 “合二为一”;而且,对于分立元件放大电路,也不再另加稳幅环节,而依靠晶体管特性的非线性来起到稳幅作用。
正弦波振荡电路常用选频网络所用元件来命名,分为 R C RC RC 正弦波振荡电路、 L C LC LC 正弦波振荡电路和石英晶体正弦波振荡电路三种类型。 R C RC RC 正弦波振荡电路的振荡频率较低,一般在 1 MHz 1\,\textrm{MHz} 1MHz 以下; L C LC LC 正弦波振荡电路的振荡频率多在 1 MHz 1\,\textrm{MHz} 1MHz 以上;石英晶体正弦波振荡电路也可等效为 L C LC LC 正弦波振荡电路,其特点是振荡频率非常稳定。
3、判断电路是否可能产生正弦波振荡的方法和步骤
(1)观察电路是否包含了放大电路、选频网络、正反馈网络和稳幅环节四个组成部分。
(2)判断放大电路是否能够正常工作,即是否有合适的静态工作点且动态信号是否能够输入、输出和放大。
(3)利用瞬时极性法判断电路是否满足正弦波振荡的相位条件。具体做法是:断开反馈,在断开处给放大电路加频率为 f 0 f_0 f0 的输入电压 U ˙ i \dot U_i U˙i,并给定其瞬时极性,如图8.1.3所示;然后以 U ˙ i \dot U_i U˙i 极性为依据判断输出电压 U ˙ o \dot U_o U˙o 的极性,从而得到反馈电压 U ˙ f \dot U_f U˙f 的极性;若 U ˙ f \dot U_f U˙f 与 U ˙ i \dot U_i U˙i 极性相同,则说明满足相位条件,电路有可能产生正弦波振荡,否则表明不满足相位条件,电路不可能产生正弦波振荡。
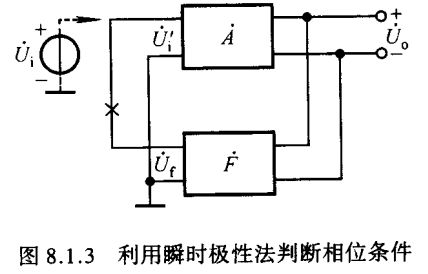
(4)判断电路是否满足正弦波振荡的幅值条件,即是否满足起振条件。具体方法是:分别求解电路的 A ˙ \dot A A˙ 和 F ˙ \dot F F˙,然后判断 ∣ A ˙ F ˙ ∣ |\dot A\dot F| ∣A˙F˙∣ 是否大于 1。只有在电路满足相位条件的情况下,判断是否满足幅值条件才有意义。换言之,若电路不满足相位条件,则电路不可能振荡,也就无需判断幅值条件了。
二、RC 正弦波振荡电路
实用的 RC 正弦波振荡电路多种多样,但最具典型性的是 RC 桥式正弦波振荡电路,在文献中也称之为文氏桥振荡电路。
1、RC 串并联选频网络
将电阻 R 1 R_1 R1 与电容 C 1 C_1 C1 串联、电阻 R 2 R_2 R2 与电容 C 2 C_2 C2 并联所组成的网络称为 R C RC RC 串并联选频网络,如图8.1.4(a)所示。通常,选取 R 1 = R 2 = R R_1=R_2=R R1=R2=R, C 1 = C 2 = C C_1=C_2=C C1=C2=C。因为 R C RC RC 串并联选频网络在正弦波振荡电路中既为选频网络,又为正反馈网络,所以其输入电压为 U ˙ o \dot U_o U˙o,输出电压为 U ˙ f \dot U_f U˙f。
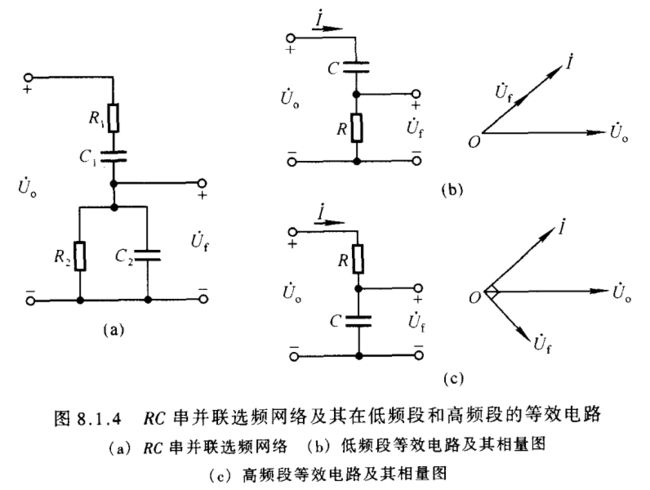
当信号频率足够低时, 1 ω C > > R \displaystyle\frac{1}{\omega C}>>R ωC1>>R,因而网络的简化电路及其电压和电流的相量图如图(b)所示。 U ˙ f \dot U_f U˙f 超前 U ˙ o \dot U_o U˙o,当频率趋近于零时,相位超前趋近于 + 90 ° + \,90° +90°,且 ∣ U ˙ f ∣ |\dot U_f| ∣U˙f∣ 趋近于零。
当信号频率足够高时, 1 ω C < < R \displaystyle\frac{1}{\omega C}<
所以,当信号频率从零逐渐变化到无穷大时, U ˙ f \dot U_f U˙f 的相位将从 + 90 ° +\,90° +90° 逐渐变化到 − 90 ° -\,90° −90°。因此,对于 R C RC RC 串并联选频网络,必定存在一个频率 f 0 f_0 f0,当 f = f 0 f=f_0 f=f0 时, U ˙ f \dot U_f U˙f 与 U ˙ o \dot U_o U˙o 同相。通过计算,可以求出 R C RC RC 串并联选频网络的频率特性和 f 0 f_0 f0。 F ˙ = U ˙ f U ˙ o = R / / 1 j ω C R + 1 j ω C + R / / 1 j ω C \dot F=\frac{\dot U_f}{\dot U_o}=\frac{R//\displaystyle\frac{1}{j\omega C}}{R+\displaystyle\frac{1}{j\omega C}+R//\frac{1}{j\omega C}} F˙=U˙oU˙f=R+jωC1+R//jωC1R//jωC1整理,可得 F ˙ = 1 3 + j ( ω R C − 1 ω R C ) \dot F=\frac{1}{3+j(\omega RC-\displaystyle\frac{1}{\omega RC})} F˙=3+j(ωRC−ωRC1)1令 ω 0 = 1 R C \omega_0=\displaystyle\frac{1}{RC} ω0=RC1,则 f 0 = 1 2 π R C ( 8.1.4 ) f_0=\frac{1}{2πRC}\kern 40pt(8.1.4) f0=2πRC1(8.1.4)代入上式,得出 F ˙ = 1 3 + j ( f f 0 − f 0 f ) ( 8.1.5 ) \dot F=\frac{1}{3+j\Big(\displaystyle\frac{f}{f_0}-\frac{f_0}{f}\Big)}\kern 20pt(8.1.5) F˙=3+j(f0f−ff0)1(8.1.5)幅频特性为 ∣ F ˙ ∣ = 1 3 2 + ( f f 0 − f 0 f ) 2 ( 8.1.6 ) |\dot F|=\frac{1}{\sqrt{3^2+\Big(\displaystyle\frac{f}{f_0}-\frac{f_0}{f}\Big)^2}}\kern 20pt(8.1.6) ∣F˙∣=32+(f0f−ff0)21(8.1.6)相频特性为 φ F = − arctan 1 3 ( f f 0 − f 0 f ) ( 8.1.7 ) \varphi_{\scriptscriptstyle F}=-\arctan\frac{1}{3}\Big(\frac{f}{f_0}-\frac{f_0}{f}\Big)\kern 20pt(8.1.7) φF=−arctan31(f0f−ff0)(8.1.7)根据式(8.1.6)、(8.1.7)画出 F ˙ \dot F F˙ 的频率特性,如图8.1.5所示。当 f = f 0 f=f_0 f=f0 时, F ˙ = 1 3 \dot F=\displaystyle\frac{1}{3} F˙=31,即 ∣ U ˙ f ∣ = 1 3 ∣ U ˙ o ∣ |\dot U_f|=\displaystyle\frac{1}{3}|\dot U_o| ∣U˙f∣=31∣U˙o∣, φ F = 0 ° \varphi_{\scriptscriptstyle F}=0° φF=0°。
2、RC 桥式正弦波振荡电路
根据式(8.1.1),因为当 f = f 0 f=f_0 f=f0 时, F ˙ = 1 3 \dot F=\displaystyle\frac{1}{3} F˙=31,所以 A ˙ = A ˙ u = 3 ( 8.1.8 ) \dot A=\dot A_u=3\kern 40pt(8.1.8) A˙=A˙u=3(8.1.8)式(8.1.8)表明,只要为 RC 串并联选频网络匹配一个电压放大倍数等于 3(即输出电压与输入电压同相,且放大倍数的数值为 3)的放大电路就可以构成正弦波振荡电路,如图8.1.6所示。考虑到起振条件,所选放大电路的电压放大倍数应略大于 3。
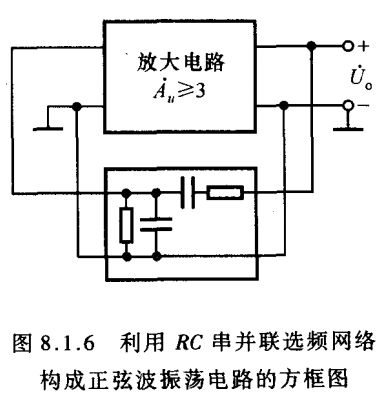
从理论上讲,任何满足放大倍数要求的放大电路与 RC 串并联选频网络都可组成正弦波振荡电路;但是,实际上,所选用的放大电路应具有尽可能大的输入电阻和尽可能小的输出电阻,以减小放大电路对选频特性的影响,使振荡频率几乎仅仅决定于选频网络。因此,通常选用引入电压串联负反馈的放大电路,如同相比例运算电路。
由 RC 串并联选频网络和同相比例运算电路所构成的 RC 桥式正弦波振荡电路如图8.1.7(a)所示。观察电路,负反馈网络的 R 1 R_1 R1、 R f R_f Rf,以及正反馈网络串联的 R R R 和 C C C、并联的 R R R 和 C C C 各为一臂构成桥路,故此得名。集成运放的输出端和 “地” 接桥路的两个顶点作为电路的输出;集成运放的同相输入端和反向输入端接另外两个顶点,是集成运放的净输入电压;如图(b)所示。

正反馈网络的反馈电压 U ˙ f \dot U_f U˙f 是同相比例运算电路的输入电压,因而要把同相比例运算电路作为整体看成电压放大电路,它的比例系数是电压放大倍数,根据起振条件和幅值平衡条件 A ˙ u = U ˙ o U ˙ p = 1 + R f R 1 ≥ 3 \dot A_u=\frac{\dot U_o}{\dot U_p}=1+\frac{R_f}{R_1}\geq3 A˙u=U˙pU˙o=1+R1Rf≥3 R f ≥ 2 R 1 ( 8.1.9 ) R_f\geq2R_1\kern 50pt(8.1.9) Rf≥2R1(8.1.9) R f R_f Rf 的取值要略大于 2 R 1 2R_1 2R1。应当指出,由于 U o U_o Uo 与 U f U_f Uf 具有良好的线性关系,所以为了稳定输出电压的幅值,一般应在电路中加入非线性环节。例如,可选用 R 1 R_1 R1 为正温度系数的热敏电阻,当 U o U_o Uo 因某种原因而增大时,流过 R f R_f Rf 和 R 1 R_1 R1 上的电流增大, R 1 R_1 R1 上的功耗随之增大,导致温度升高,因而 R 1 R_1 R1 的阻值增大,从而使得 A ˙ u \dot A_u A˙u 数值减小, U o U_o Uo 也就随之减小;当 U o U_o Uo 因某种原因而减小时,各物理量与上述变化相反,从而使输出电压稳定。当然,也可选用 R f R_f Rf 为负温度系数的热敏电阻。
此外,还可在 R f R_f Rf 回路串联两个并联的二极管,如图8.1.8所示,利用电流增大时二极管动态电阻减小、电流减小时二极管动态电阻增大的特点,加入非线性环节,从而使输出电压稳定。此时比例系数为 A ˙ u = 1 + R f + r d R 1 ( 8.1.10 ) \dot A_u=1+\frac{R_f+r_d}{R_1}\kern 40pt(8.1.10) A˙u=1+R1Rf+rd(8.1.10)
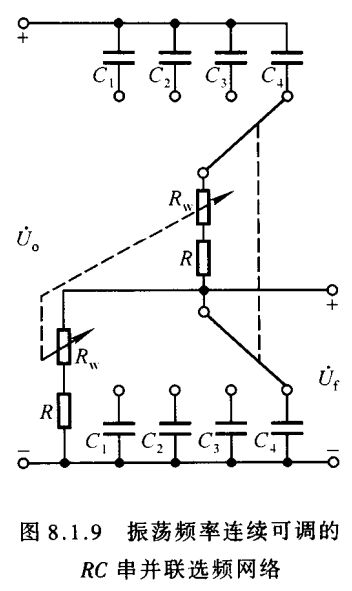
3、振荡频率可调的 RC 桥式正弦波振荡电路
为了使得振荡频率连续可调,常在 RC 串并联网络中,用双层波段开关接不通的电容,作为振荡频率 f 0 f_0 f0 的粗调;用同轴电位器实现 f 0 f_0 f0 的微调,如图8.1.9所示。振荡频率可调范围能够从几赫兹到几百千赫。
综上所述,RC 桥式正弦波振荡电路以 RC 串并联网络为选频网络和正反馈网络,以电压串联负反馈放大电路为放大环节,具有振荡频率稳定,带负载能力强,输出电压失真小等优点,因此获得相当广泛的应用。
为了提高 RC 桥式正弦波振荡电路的振荡频率,必须减小 R R R 和 C C C 的数值。然而,一方面,当 R R R 减小到一定程度时,同相比例运算电路的输出电阻将影响选频特性;另一方面,当 C C C 减小到一定程度时,晶体管的极间电容和电路的分布电容将影响选频特性;因此,振荡频率高到一定程度时,其值不仅决定于选频网络,还与放大电路的参数有关。这样, f 0 f_0 f0 不但与一些未知因素有关,而且还将受环境温度的影响。因此,当振荡频率较高时,应选用 L C LC LC 正弦波振荡电路。
【例8.1.1】在图8.1.9所示电路中,若电容的取值分别为 0.01 μF、0.1 μF、1 μF、10 μF,电阻 R = 50 Ω R=50\,Ω R=50Ω,电位器 R w = 10 kΩ R_w=10\,\textrm{kΩ} Rw=10kΩ。
试问: f 0 f_0 f0 的调节范围为多少?
解:因为 f 0 = 1 2 π R C f_0=\displaystyle\frac{1}{2πRC} f0=2πRC1,所以 f 0 f_0 f0 的最小值 f 0 m i n = 1 2 π ( R + R w ) C m a x ≈ 1.59 Hz f_{0min}=\frac{1}{2π(R+R_w)C_{max}}\approx1.59\,\textrm {Hz} f0min=2π(R+Rw)Cmax1≈1.59Hz f 0 f_0 f0 的最大值 f 0 m a x = 1 2 π R C m i n ≈ 318 kHz f_{0max}=\frac{1}{2πRC_{min}}\approx318\,\textrm{kHz} f0max=2πRCmin1≈318kHz f 0 f_0 f0 的调节范围约为 1.59 Hz ∼ 318 kHz 1.59 \,\textrm{Hz} \sim 318\,\textrm{kHz} 1.59Hz∼318kHz。
三、LC 正弦波振荡电路
LC 正弦波振荡电路与 RC 桥式正弦波振荡电路的组成原则在本质上是相同的,只是选频网络采用 LC 电路。在 LC 振荡电路中,当 f = f 0 f=f_0 f=f0 时,放大电路的放大倍数数值最大,而其余频率的信号均被衰减到零;引入正反馈后,使反馈电压作为放大电路的输入电压,以维持输出电压,从而形成正弦波振荡。由于 LC 正弦波振荡电路的振荡频率较高,所以放大电路多采用分立元件电路,必要时还应采用共基电路。
1、LC 谐振回路的频率特性
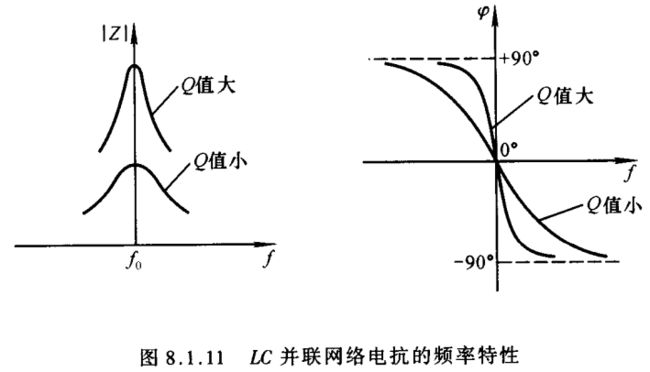
常见的 LC 正弦波振荡电路中的选频网络多采用 LC 并联网络,如图8.1.10所示。图(a)为理想电路,无损耗,谐振频率为 f 0 = 1 2 π L C f_0=\frac{1}{2π\sqrt{LC}} f0=2πLC1在信号频率较低时,电容的容抗很大,网络呈感性;在信号频率较高时,电感的感抗很大,网络呈容性;只有 f = f 0 f=f_0 f=f0 时,网络才呈纯阻性,且阻抗无穷大。这时电路产生电流谐振,电容的电场能转换成磁场能,而电感的磁场能又转换成电场能,两种能量相互转换。

实际的 LC 并联网络总是有损耗的,各种损耗等效成电阻 R R R,如图(b)所示。电路的导纳为 Y = j ω C + 1 R + j ω L = R R 2 + ( ω L ) 2 + j [ ω C − ω L R 2 + ( ω L ) 2 ] ( 8.1.11 ) Y=j\omega C+\frac{1}{R+j\omega L}=\frac{R}{R^2+(\omega L)^2}+j\Big[\omega C-\frac{\omega L}{R^2+(\omega L)^2}\Big]\kern 10pt(8.1.11) Y=jωC+R+jωL1=R2+(ωL)2R+j[ωC−R2+(ωL)2ωL](8.1.11)令式中虚部为零,就可求出谐振角频率 ω 0 = 1 1 + ( R ω 0 L ) 2 ⋅ 1 L C = 1 1 + 1 Q 2 ⋅ L C \omega_0=\frac{1}{\sqrt{1+\Big(\displaystyle\frac{R}{\omega_0L}\Big)^2}}\cdot\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{1+\displaystyle\frac{1}{Q^2}}\cdot\sqrt{LC}} ω0=1+(ω0LR)21⋅LC1=1+Q21⋅LC1式中 Q Q Q 为品质因数 Q = ω 0 L R ( 8.1.12 ) Q=\frac{\omega_0L}{R}\kern 40pt(8.1.12) Q=Rω0L(8.1.12)当 Q > > 1 Q>>1 Q>>1 时, ω 0 ≈ 1 L C \omega_0\approx\displaystyle\frac{1}{\sqrt{LC}} ω0≈LC1,所以谐振频率 f 0 ≈ 1 2 π L C ( 8.1.13 ) f_0\approx\frac{1}{2π\sqrt{LC}}\kern 40pt(8.1.13) f0≈2πLC1(8.1.13)上述条件下的品质因数 Q ≈ 1 R L C ( 8.1.14 ) Q\approx\frac{1}{R}\sqrt{\frac{L}{C}}\kern 40pt(8.1.14) Q≈R1CL(8.1.14)式(8.1.14)表明,选频网络的损耗愈小;谐振频率相同时,电容容量愈小,电感数值愈大,品质因数愈大,将使得选频特性愈好。
当 f = f 0 f=f_0 f=f0 时,电抗 Z 0 = 1 Y 0 = R 2 + ( ω 0 L ) 2 R = R + Q 2 R Z_0=\frac{1}{Y_0}=\frac{R^2+(\omega_0L)^2}{R}=R+Q^2R Z0=Y01=RR2+(ω0L)2=R+Q2R当 Q > > 1 Q>>1 Q>>1 时, Z 0 ≈ Q 2 R Z_0\approx Q^2R Z0≈Q2R,将式(8.1.14)代入,整理可得 Z 0 ≈ Q X L ≈ Q X C ( 8.1.15 ) Z_0\approx QX_L\approx QX_C\kern 30pt(8.1.15) Z0≈QXL≈QXC(8.1.15) X L X_L XL 和 X C X_C XC 分别是电感和电容的电抗。因此,当网络的输入电流为 I 0 I_0 I0 时,电容和电感的电流约为 Q I 0 QI_0 QI0。
根据式(8.1.11),可得适用于频率从零到无穷大时 LC 并联网络电抗的表达式, Z = 1 Y Z=\frac{1}{Y} Z=Y1 Z Z Z 是频率的函数,其频率特性如图8.1.11所示。 Q Q Q 值愈大,曲线愈陡,选频特性愈好。
若以 L C LC LC 并联网络作为共射放大电路的集电极负载,如图8.1.12所示,则电路的电压放大倍数 A ˙ u = − β Z r b e \dot A_u=-\beta\frac{Z}{r_{be}} A˙u=−βrbeZ
根据 LC并联网络的频率特性,当 f = f 0 f=f_0 f=f0 时,电压放大倍数的数值最大,且无附加相移。对于其余频率的信号,电压放大倍数不但数值减小,而且有附加相移。电路具有选频特性,故称之为选频放大电路。若在电路中引入正反馈,并能用反馈电压取代输入电压,则电路就成为正弦波振荡电路。根据引入反馈的方式不同,LC 正弦波振荡电路分为变压器反馈式、电感反馈式和电容反馈式三种电路;所用放大电路视振荡频率而定,可以是共射电路,也可以是共基电路。
2、变压器反馈式振荡电路
(1)工作原理
引入正反馈最简单的方法是采用变压器反馈方式,如图8.1.13所示;为使反馈电压与输入电压同相,同名端如图中所标注。当反馈电压取代输入电压时,就得到变压器反馈式振荡电路,如图8.1.14所示。
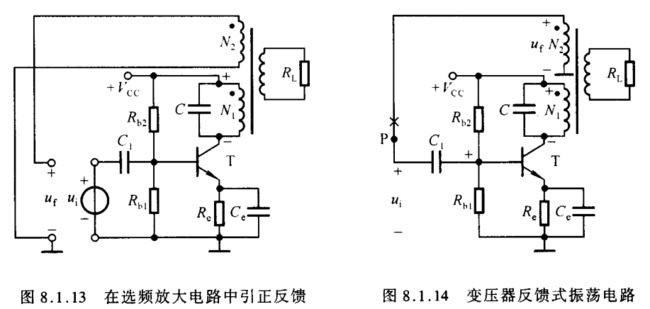
对于图8.1.14所示电路,可以用前面所叙述的方法判断产生正弦波振荡的可能性。首先,观察电路,存在放大电路、选频网络、正反馈网络以及用晶体管的非线性特性所实现的稳幅环节四个部分。然后,判断放大电路能否正常工作,图中放大电路是典型的工作点稳定电路,可以设置合适的静态工作点;电路的交流通路如图8.1.15所示,交流信号传递过程中无开路或短路现象,电路可以正常放大。最后,采用瞬时极性法判断电路是否满足相位平衡条件。在图8.1.15中,断开 P 点,加 f = f 0 f=f_0 f=f0 的输入电压,规定其极性,得到变压器原边线圈 N 1 N_1 N1 电压的极性,进而得到副边线圈 N 2 N_2 N2 电压的极性,如图中所标注,故电路满足相位条件,有可能产生正弦波振荡。
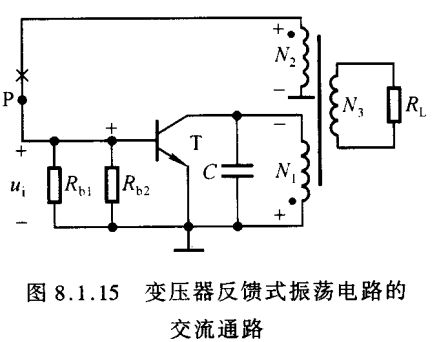
而在多数情况下,不必画出交流通路就可判断电路是否满足相位条件。具体做法是:在图8.1.14所示电路中,断开 P 点,在断开处给放大电路加 f = f 0 f=f_0 f=f0 的输入电压 U ˙ i \dot U_i U˙i,给定其极性对 “地” 为正,因而晶体管基极动态电位对 “地” 为正,由于放大电路为共射接法,故集电极动态电位对 “地” 为负;对于交流信号,电源相当于 “地”,所以线圈 N 1 N_1 N1 上电压为上 “正” 下 “负”;根据同名端, N 2 N_2 N2 上电压也为上 “正” 下 “负”,即反馈电压对 “地” 为正,与输入电压假设极性相同,满足正弦波振荡的相位条件。
图8.1.14所示电路表明,变压器反馈式振荡电路中放大电路的输入电阻是放大电路负载的一部分,因此 A ˙ \dot A A˙ 与 F ˙ \dot F F˙ 相互关联。一般情况下,只要合理选择变压器原、副边线圈的匝数比以及其它电路参数,电路很容易满足幅值条件。
(2)振荡频率及起振条件
图8.1.14所示变压器反馈式振荡电路的交流等效电路如图8.1.16所示。 R R R 是 L C LC LC 谐振回路、负载等的总损耗, L 1 L_1 L1 为考虑到 N 3 N_3 N3 回路参数折合到原边的等效电感, L 2 L_2 L2 为副边电感, M M M 为 N 1 N_1 N1 和 N 2 N_2 N2 之间的等效互感; R i R_i Ri 为放大电路的输入电阻,其值 R i = R b 1 / / R b 2 / / r b e R_i=R_{b1}//R_{b2}//r_{be} Ri=Rb1//Rb2//rbe。
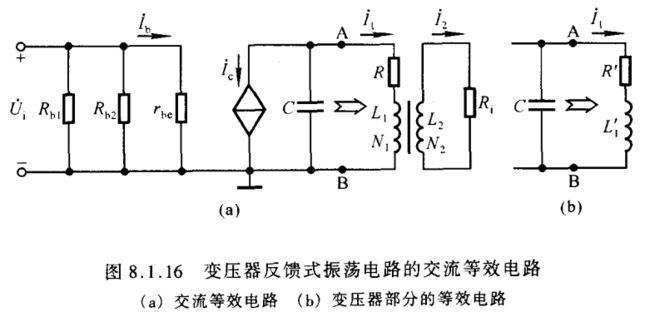
为了分析振荡频率和起振条件,首先求解图(a)中从 A 和 B 两点向右看进去的等效电路及其参数。在变压器原边 U ˙ o = ( R + j ω L 1 ) I ˙ 1 − j ω M I ˙ 2 ( 8.1.16 ) \dot U_o=(R+j\omega L_1)\dot I_1-j\omega M\dot I_2\kern 20pt(8.1.16) U˙o=(R+jωL1)I˙1−jωMI˙2(8.1.16)在副边,电流 I ˙ 2 = j ω M I ˙ 1 R i + j ω L 2 ( 8.1.17 ) \dot I_2=\frac{j\omega M\dot I_1}{R_i+j\omega L_2}\kern 40pt(8.1.17) I˙2=Ri+jωL2jωMI˙1(8.1.17)将式(8.1.17)代入式(8.1.16),整理可得 U ˙ o = ( R ′ + j ω L 1 ′ ) I ˙ 1 ( 8.1.18 ) \dot U_o=(R'+j\omega L'_1)\dot I_1\kern 30pt(8.1.18) U˙o=(R′+jωL1′)I˙1(8.1.18)其中 { R ′ = R + ω 2 M 2 R i 2 + ω 2 L 2 2 ⋅ R i ( 8.1.19 a ) L 1 ′ = L 1 − ω 2 M 2 R i 2 + ω 2 L 2 2 ⋅ L 2 ( 8.1.19 b ) \left\{\begin{matrix}R'=R+\displaystyle\frac{\omega^2M^2}{R^2_i+\omega^2L^2_2}\cdot R_i\kern 30pt(8.1.19a)\\L'_1=L_1-\displaystyle\frac{\omega^2M^2}{R^2_i+\omega^2L^2_2}\cdot L_2\kern 24pt(8.1.19b)\end{matrix}\right. ⎩ ⎨ ⎧R′=R+Ri2+ω2L22ω2M2⋅Ri(8.1.19a)L1′=L1−Ri2+ω2L22ω2M2⋅L2(8.1.19b)因此,从变压器原边向副边看进去的等效电路如图8.1.16(b)所示,为典型的 L C LC LC 谐振回路。但与之相比,带负载后,电感量变小,损耗变大,因而品质因数变小,选频特性变差。其品质因数 Q ≈ 1 R ′ L 1 ′ C ( 8.1.20 ) Q\approx\frac{1}{R'}\sqrt{\frac{L'_1}{C}}\kern 50pt(8.1.20) Q≈R′1CL1′(8.1.20)当 Q > > 1 Q>>1 Q>>1 时,谐振频率 f 0 ≈ 1 2 π L 1 ′ C ( 8.1.21 ) f_0\approx\frac{1}{2π\sqrt{L'_1C}}\kern 50pt(8.1.21) f0≈2πL1′C1(8.1.21)根据前面的分析可知,在谐振频率下, L 1 L_1 L1 中电流的数值约为晶体管集电极电流的 Q Q Q 倍,即 ∣ I ˙ 1 ∣ ≈ Q ∣ I ˙ c ∣ = Q β ∣ I ˙ b ∣ = Q β ∣ U ˙ i ∣ r b e |\dot I_1|\approx Q|\dot I_c|=Q\beta|\dot I_b|=Q\beta\frac{|\dot U_i|}{r_{be}} ∣I˙1∣≈Q∣I˙c∣=Qβ∣I˙b∣=Qβrbe∣U˙i∣根据式(8.1.17),反馈电压 U ˙ f = I ˙ f R i = j ω 0 M I ˙ 1 R i + j ω 0 L 2 ⋅ R i \dot U_f=\dot I_fR_i=\frac{j\omega_0 M\dot I_1}{R_i+j\omega_0L_2}\cdot R_i U˙f=I˙fRi=Ri+jω0L2jω0MI˙1⋅Ri通常, ω 0 L 2 < < R i \omega_0L_2<
若将式(8.1.20)、(8.1.21)代入,则得出起振条件为 β > r b e R ′ C M ( 8.1.23 ) \beta>\frac{r_{be}R'C}{M}\kern 50pt(8.1.23) β>MrbeR′C(8.1.23)
(3)优缺点
变压器反馈式振荡电路易于产生振荡,波形较好,应用范围广泛。但是由于输出电压与反馈电压靠近磁路耦合,因而耦合不紧密,损耗较大。并且振荡频率的稳定性不高。
3、电感反馈式振荡电路
(1)电路组成
为了克服变压器反馈式振荡电路中变压器原边线圈和副边线圈耦合不紧密的缺点,可将 N 1 N_1 N1 和 N 2 N_2 N2 合并为一个线圈,把图8.1.14所示电路中线圈 N 1 N_1 N1 接电源的一端和 N 2 N_2 N2 接地的一端相连作为中间抽头;为了加强谐振效果,将电容 C C C 跨接在整个线圈两端,如图8.1.17所示。

(2)工作原理
利用判断电路能否产生正弦波振荡的方法来分析图8.1.17所示电路。首先观察电路,它包含了放大电路、选频网络、反馈网络和非线性元件——晶体管四个部分,而且放大电路能够正常工作。然后用瞬时极性法判断电路是否满足正弦波振荡的相位条件:断开反馈,加频率为 f 0 f_0 f0 的输入电压,给定其极性,判断出从 N 2 N_2 N2 上获得的反馈电压极性与输入电压相同,故电路满足正弦波振荡的相位条件,各点瞬时极性如图中所标注。只要电路参数选择得当,电路就可满足幅值条件,而产生正弦波振荡。
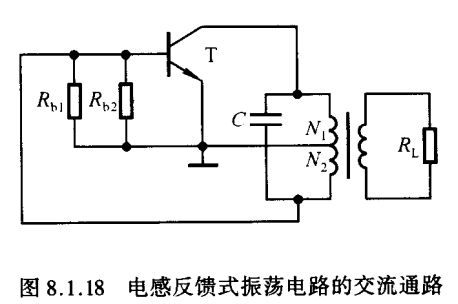
图8.1.18所示为电感反馈式振荡电路的交流通路,原边线圈的三个端分别接到晶体管的三个极,故称电感反馈式振荡电路为电感三点式电路。
(3)振荡频率和起振条件
断开反馈且带载情况下的交流等效电路如图8.1.19所示。
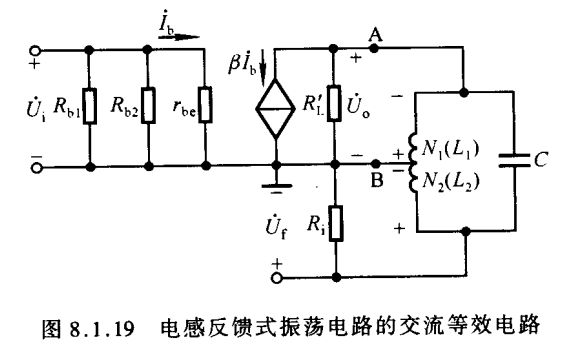
R i R_i Ri 作为 N 2 N_2 N2 的负载,其值放大电路的输入电阻, R i = R b 1 / / R b 2 / / r b e R_i=R_{b1}//R_{b2}//r_{be} Ri=Rb1//Rb2//rbe。
设 N 1 N_1 N1 的电感量为 L 1 L_1 L1, N 2 N_2 N2 的电感量为 L 2 L_2 L2, N 1 N_1 N1 与 N 2 N_2 N2 间的互感为 M M M,且品质因数远大于 1,则振荡频率 f 0 ≈ 1 2 π ( L 1 + L 2 + 2 M ) C ( 8.1.24 ) f_0\approx\frac{1}{2π\sqrt{(L_1+L_2+2M)C}}\kern 25pt(8.1.24) f0≈2π(L1+L2+2M)C1(8.1.24)反馈系数的数值 ∣ F ˙ ∣ = ∣ U ˙ f U ˙ o ∣ ≈ j ω L 2 + j ω M j ω L 1 + j ω M = L 2 + M L 1 + M ( 8.1.25 ) |\dot F|=\Big|\frac{\dot U_f}{\dot U_o}\Big|\approx\frac{j\omega L_2+j\omega M}{j\omega L_1+j\omega M}=\frac{L_2+M}{L_1+M}\kern 20pt(8.1.25) ∣F˙∣= U˙oU˙f ≈jωL1+jωMjωL2+jωM=L1+ML2+M(8.1.25)因而,将 R i R_i Ri 等效到 A 和 B 两端为 R i ′ R'_i Ri′,根据等效前后的功率相等 ∣ U ˙ o ∣ 2 R i ′ = ∣ U ˙ f ∣ 2 R i \frac{|\dot U_o|^2}{R'_i}=\frac{|\dot U_f|^2}{R_i} Ri′∣U˙o∣2=Ri∣U˙f∣2整理可得 R i ′ = R i ∣ F ˙ ∣ 2 ( 8.1.26 ) R'_i=\frac{R_i}{|\dot F|^2}\kern 60pt(8.1.26) Ri′=∣F˙∣2Ri(8.1.26)设 R L ′ R'_L RL′ 是 R L R_L RL 折合到 A、B 两点间的等效负载,则集电极总负载 R L ′ ′ = R L ′ / / R i ′ ( 8.1.27 ) R''_L=R'_L//R'_i\kern 40pt(8.1.27) RL′′=RL′//Ri′(8.1.27)当 f = f 0 f=f_0 f=f0 且 Q > > 1 Q>>1 Q>>1 时, L C LC LC 回路产生谐振,等效电阻非常大,所取电流可忽略不计,因此放大电路的电压放大倍数 A ˙ u = − β R L ′ ′ r b e ( 8.1.28 ) \dot A_u=-\beta\frac{R''_L}{r_{be}}\kern 40pt(8.1.28) A˙u=−βrbeRL′′(8.1.28)根据 ∣ A ˙ F ˙ ∣ > 1 |\dot A\dot F|>1 ∣A˙F˙∣>1,利用式(8.1.25)和(8.1.28),可得起振条件为 β > L 1 + M L 2 + M ⋅ r b e R L ′ ′ ( 8.1.29 ) \beta>\frac{L_1+M}{L_2+M}\cdot\frac{r_{be}}{R''_L}\kern 30pt(8.1.29) β>L2+ML1+M⋅RL′′rbe(8.1.29)从式(8.1.25)、(8.1.28)、(8.1.29)可以看出,若增大 L 2 L_2 L2 与 L 1 L_1 L1 的比值,则一方面 ∣ F ˙ ∣ |\dot F| ∣F˙∣ 随之增大,有利于电路起振;另一方面,它又使 R L ′ ′ R''_L RL′′ 减小,从而使 ∣ A ˙ u ∣ |\dot A_u| ∣A˙u∣ 减小,不利于电路起振。所以, L 2 / L 1 L_2/L_1 L2/L1 既不能太大,也不能太小。在大批量生产时,应通过实验确定 N 2 N_2 N2 与 N 1 N_1 N1 的比值,一般在 1 / 7 ∼ 1 / 4 1/7\sim 1/4 1/7∼1/4 之间。
(4)优缺点
电感反馈式振荡电路中 N 2 N_2 N2 与 N 1 N_1 N1 之间耦合紧密,振幅大;当 C C C 采用可变电容时,可以获得调节范围较宽的振荡频率,最高振荡频率可达几十兆赫。由于反馈电压取自电感,对高频信号具有较大的电抗,输出电压波形中常含有高次谐波。因此,电感反馈式振荡电路常用在对波形要求不高的设备之中,如高频加热器、接收机的本机振荡器等。
4、电容反馈式振荡电路
(1)电路组成
为了获得较好的输出电压波形,若将电感反馈式振荡电路中的电容换成电感,电感换成电容,并在置换后将两个电容的公共端接地,且增加集电极电阻 R c R_c Rc,就可得到电容反馈式振荡电路,如图8.1.20所示。因为两个电容的三个端分别接晶体管的三个极,故也称之为电容三点式电路。

(2)工作原理
根据正弦波振荡电路的判断方法,观察图8.1.20所示电路,包含了放大电路、选频网络、反馈网络和非线性元件——晶体管四个部分,而且放大电路能够正常工作。断开反馈,加频率为 f 0 f_0 f0 的输入电压,给定其极性,判断从 C 2 C_2 C2 上所获得的反馈电压的极性与输入电压相同,故电路满足正弦波振荡的相位条件,各点瞬时极性如图中所标注。只要电路参数选择得当,电路就可满足幅值条件,而产生正弦波振荡。
(3)振荡频率和起振条件
当由 L L L、 C 1 C_1 C1 和 C 2 C_2 C2 所构成的选频网络的品质因数 Q Q Q 远大于 1 时,振荡频率 f 0 ≈ 1 2 π L C 1 C 2 C 1 + C 2 ( 8.1.30 ) f_0\approx\frac{1}{2π\sqrt{L\displaystyle\frac{C_1C_2}{C_1+C_2}}}\kern 40pt(8.1.30) f0≈2πLC1+C2C1C21(8.1.30)设 C 1 C_1 C1 和 C 2 C_2 C2 的电流分别为 I ˙ C 1 \dot I_{\scriptscriptstyle C1} I˙C1 和 I ˙ C 2 \dot I_{\scriptscriptstyle C2} I˙C2,当发生并联谐振时,谐振网络里的电流远大于外部支路电路,所以 I ˙ C 1 ≈ I ˙ C 2 \dot I_{\scriptscriptstyle C1}\approx \dot I_{C2} I˙C1≈I˙C2,则反馈系数 ∣ F ˙ ∣ = ∣ U ˙ f U ˙ o ∣ = ∣ I ˙ C 2 / j ω C 2 I ˙ C 1 / j ω C 1 ∣ ≈ C 1 C 2 ( 8.1.31 ) |\dot F|=\Big|\frac{\dot U_f}{\dot U_o}\Big|=\Big|\frac{\dot I_{\scriptscriptstyle C2}/j\omega C_2}{\dot I_{\scriptscriptstyle C1}/j\omega C_1}\Big|\approx\frac{C_1}{C_2}\kern 20pt(8.1.31) ∣F˙∣= U˙oU˙f = I˙C1/jωC1I˙C2/jωC2 ≈C2C1(8.1.31)电压放大倍数 ∣ A ˙ u ∣ = ∣ U ˙ o U ˙ i ∣ = β R L ′ r b e ( 8.1.32 ) |\dot A_u|=\Big|\frac{\dot U_o}{\dot U_i}\Big|=\beta\frac{R'_L}{r_{be}}\kern 40pt(8.1.32) ∣A˙u∣= U˙iU˙o =βrbeRL′(8.1.32)在空载情况下,类比式(8.1.26)可知,式(8.1.32)中集电极等效负载 R L ′ = R c / / R i ∣ F ˙ ∣ 2 R'_L=R_c//\frac{R_i}{|\dot F|^2} RL′=Rc//∣F˙∣2Ri根据 ∣ A ˙ F ˙ ∣ > 1 |\dot A\dot F|>1 ∣A˙F˙∣>1,利用式(8.1.31)和(8.1.32),可得起振条件为 β > C 2 C 1 ⋅ r b e R L ′ ( 8.1.33 ) \beta>\frac{C_2}{C_1}\cdot\frac{r_{be}}{R'_L}\kern 40pt(8.1.33) β>C1C2⋅RL′rbe(8.1.33)与电感反馈式振荡电路相类似,若增大 C 1 / C 2 C_1/C_2 C1/C2,则一方面反馈系数数值随之增大,有利于电路起振;另一方面,它又使 R L ′ R'_L RL′ 减小,从而造成电压放大倍数数值减小,不利于电路起振。因此 C 1 / C 2 C_1/C_2 C1/C2 既不能太大,又不能太小,具体数值应通过实验来确定。
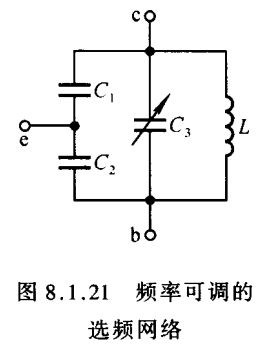
电容反馈式振荡电路的输出电压波形好,但若用改变电容的方法来调解振荡频率,则会影响电路的起振条件;而若用改变电感的方法来调解振荡频率,则比较困难。所以常常用在固定振荡频率的场合。在振荡频率可调范围不大的情况下,可采用图8.1.21所示电路取代图8.1.20所示电路中的选频网络。
(4)稳定振荡频率的措施

若要提高电容反馈式振荡电路的振荡频率,则势必要减小 C 1 C_1 C1、 C 2 C_2 C2 的电容量和 L L L 的电感量。实际上,当 C 1 C_1 C1 和 C 2 C_2 C2 减小到一定程度时,晶体管的极间电容和电路中的杂散电容将影响振荡频率。这些电容等效为放大电路的输入电容 C i C_i Ci 和输出电容 C o C_o Co,它们分别与 C 2 C_2 C2 和 C 1 C_1 C1 并联,如图8.1.22所标注。由于极间电容受温度的影响,杂散电容又难于确定,为了稳定振荡频率,在设计电路时,必须能够使 C i C_i Ci 和 C o C_o Co 对选频特性的影响忽略不计。如果 C 1 C_1 C1 和 C 2 C_2 C2 远大于极间电容和杂散电容,只起分压作用,以便获得合适的反馈电压,而几乎对振荡频率无影响,那么电路的振荡频率就可能很稳定。具体方法是在电感所在支路串联一个小容量电容 C C C,而且 C < < C 1 C<
若要求电容反馈式振荡电路的振荡频率高达 100 MHz 以上,则要考虑采用共基放大电路,如图8.1.23所示。图中 C b C_b Cb 为旁路电容,对交流信号可视为短路;放大电路为共基放大电路。断开反馈,给放大电路加频率为 f 0 f_0 f0 的输入电压,极性为上 “+” 下 “-”;因共基放大电路输出电压与输入电压同相,故集电极动态电位为 “+”;选频网络的电压方向为上 “-” 下 “+”,因此从 C 1 C_1 C1 上获得的反馈电压也为上 “-” 下 “+”,与输入电压同相,所以电路满足正弦波振荡的相位平衡条件。如果参数合适,使电路满足起振条件,那么电路就一定会产生正弦波振荡。

由以上分析可知,在判断电路是否可能产生正弦波振荡,即判断电路是否满足正弦波振荡的相位条件时,必须弄清反馈电压取自哪个线圈或电容,而通常这个线圈或电容总有一端为交流通路的 “地”。
【例8.1.2】电路如图8.1.24所示,图中 C b C_b Cb 为旁路电容, C 1 C_1 C1 为耦合电容,对交流信号均可视为短路。为使电路可能产生正弦波振荡,试说明变压器原边线圈和副边线圈的同名端。
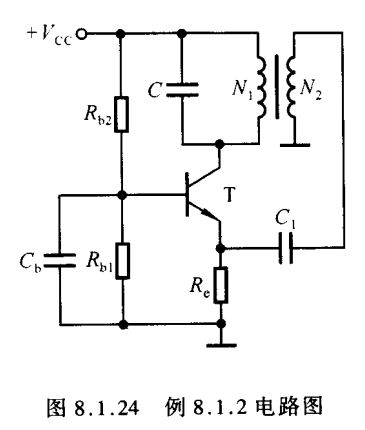
解: 图8.1.24所示电路中的放大电路为共基放大电路。断开反馈,给放大电路加频率为 f 0 f_0 f0 的输入电压,极性为上 “+” 下 “-”;集电极动态电位为 “+”,选频网络的电压极性为上 “-” 下 “+”;从变压器副边获得的反馈电压应为上 “+” 下 “-”,才满足正弦波振荡电路的相位平衡条件。因此,变压器原边线圈的下端和副边线圈的上端为同名端;或者说原边线圈的上端和副边线圈的下端为同名端。
【例8.1.3】改正图8.1.25所示电路中的错误,使之有可能产生正弦波振荡。要求不改变放大电路的基本接法。
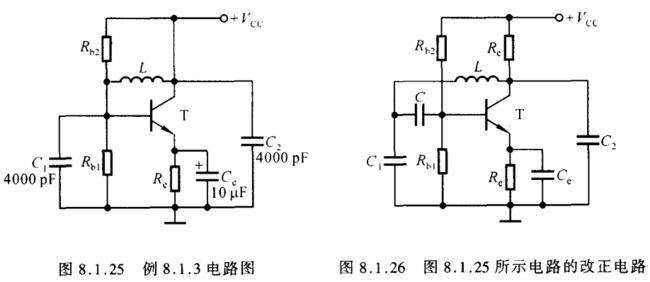
解: 观察电路, C e C_e Ce 容量远大于 C 1 C_1 C1 和 C 2 C_2 C2,故为旁路电容,对交流信号可视为短路。 C 1 C_1 C1、 C 2 C_2 C2 和 L L L 构成 L C LC LC 并联谐振网络, C 2 C_2 C2 上的电压为输出电压, C 1 C_1 C1 上的电压为反馈电压,因而电路为电容反馈式振荡电路。
电感 L L L 连接晶体管的基极和集电极,在直流通路中使两个极近似短路,均约为 + V C C +V_{CC} +VCC,造成放大电路的静态工作点不合适,故应在选频网络与放大电路输入端之间加耦合电容。
晶体管的集电极直接接电源,在交流通路中使集电极与发射极短路,因而输出电压恒等于零,所以必须在集电极加电阻 R c R_c Rc。
改正电路如图8.1.26所示,与图8.1.20所示电路相比,同为电容反馈式振荡电路,只是画法不同而已。

