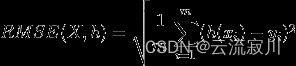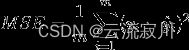数据挖掘各流程中的常用方法总结（三）

前两个小节我们分别介绍了数据的EDA过程和数据预处理阶段的常用方法，下面是本系列的最后一部分——数据建模与验证。事实上，这部分并非随意选取一个模型，拟合数据然后测试这么简单。我们应该说清楚以下几个问题：1、这是一个什么问题？
2、我们应该选取什么模型？为什么？
3、我们应当如何选定参数？
4、我们应该如何评价模型的效果？
5、模型的结果说明了什么结论？

评价指标

1、混淆矩阵

混淆矩阵是监督学习中用于评价分类效果的一种可视化工具，他以二维表的形式展示了预测类别和实例类别的交叉情况。一般地，矩阵的行代表预测类别，列代表真实类别，从上到下从左到右分别称为：真阳（TP）、假阳（FP）、假阴（FN）、真阴（TN）。特别的，一般会考察真阳率，又叫灵敏度：TP/TP+FN，真阴率，又叫特异度：TN/TN+FP

2、准确率（Accuracy）

准确率是最常用的分类性能指标。 Accuracy = (TP+TN)/(TP+FN+FP+TN) 即正确预测的正反例数 /总数

3、精确率（Precision）

精确率容易和准确率被混为一谈。其实，精确率只是针对预测正确的正样本而不是所有预测正确的样本。表现为预测出是正的里面有多少真正是正的。可理解为查准率。 Precision = TP/(TP+FP) 即正确预测的正例数 /预测正例总数

4、召回率（Recall）

召回率表现出在真实为正的样本中，也被预测为正的有多少，可理解为查全率。 Recall = TP/(TP+FN)，即正确预测的正例数 /预测正例总数。

5、F1 score

F值是精确率和召回率的调和值，更接近于两个数较小的那个，所以精确率和召回率接近时，F值最大。很多推荐系统的评测指标就是用F值的。 2/F1 = 1/Precision + 1/Recall

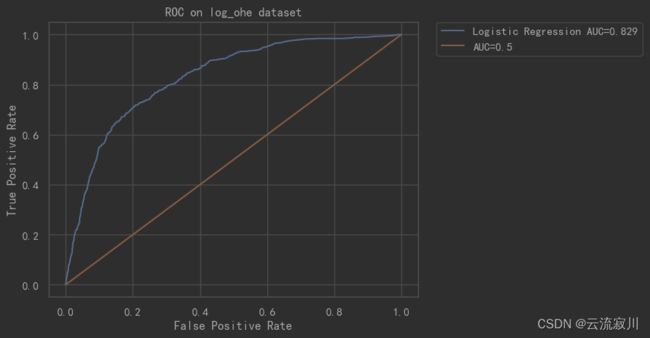
6、AUC

AUC（Area Under Curve）被定义为ROC曲线下的面积(ROC的积分)，通常大于0.5小于1。随机挑选一个正样本以及一个负样本，分类器判定正样本的值高于负样本的概率就是 AUC 值。AUC值(面积)越大的分类器，性能越好

7、RMSE（均方根误差）、MSE（均方误差）、MAE（平均绝对误差）

RMSE（Root Mean Square Error）均方根误差

衡量观测值与真实值之间的偏差，常用来作为机器学习模型预测结果衡量的标准。

MSE（Mean Square Error）均方误差

MSE是真实值与预测值的差值的平方然后求和平均。

通过平方的形式便于求导，所以常被用作线性回归的损失函数。

MAE（Mean Absolute Error）平均绝对误差

是绝对误差的平均值。

可以更好地反映预测值误差的实际情况。

下面以代码的形式介绍，RMSE和AUC曲线的计算和绘制：

RMSE：

sklearn中的参数scoring下，均方误差作为评判 标准时，却是计算”负均方误差“(neg_mean_squared_error)。这是因为sklearn在计算模型评估指标的时候，会考虑指标本身的性质，均方误差本身是一种误差，所以被sklearn划分为模型的一种损失(loss)。在sklearn当中，所有的损失都使用负数表示，因此均方误差也被显示为负数了

def rmsle_cv(model):
    kf = KFold(n_splits=5,shuffle=True,random_state=42).get_n_splits(train.values)
    print("kf={}".format(kf))
    rmse = np.sqrt(-cross_val_score(model,train.values,y_train,scoring='neg_mean_squared_error',cv=kf))
    return rmse

AUC:

fpr, tpr, threshold = roc_curve(y_true, y_pred)
sns.lineplot(fpr, tpr, label=label_1)
x = np.arange(0, 1.1, 0.1)  # 绘制AUC=0.5的直线
sns.lineplot(x, x, label="AUC=0.5")
plt.title("ROC on %s dataset" % (dataset))
plt.xlabel('False Positive Rate')
plt.ylabel("True Positive Rate")
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)  # 设置图例在图形外
plt.show()

示例如下：

模型调参

事实上，调参方面往往是提升模型预测或分类能力的一个重要途径，前面对数据进行大量的分析和预处理工作本质上还是优化杂乱无章的数据使得训练集易于被模型拟合。但是当前的数据使得什么样的模型，或者说在什么模型中表现最佳，我们无法通过简单的分析和计算感知到，因此就需要引入调参过程。

在机器学习模型中，需要人工选择的参数称为超参数。比如随机森林中决策树的个数，人工神经网络模型中隐藏层层数和每层的节点个数，正则项中常数大小等等，他们都需要事先指定。超参数选择不恰当，就会出现欠拟合或者过拟合的问题。而在选择超参数的时候，有两个途径，一个是凭经验微调，另一个就是选择不同大小的参数，带入模型中，挑选表现最好的参数。

微调的一种方法是手工调制超参数，直到找到一个好的超参数组合，这么做的话会非常冗长，你也可能没有时间探索多种组合，所以可以使用Scikit-Learn的GridSearchCV和RandomizedSearchCV来自动完成。

网格搜索（GridSearchCV）

顾名思义，网格搜索就是网格化的一一查找。它采用穷举的思想，每一个超参数就是网格中的一个维度，所有维度中每一对参数值的组合就是网格中的一个点，GridSearchCV按照步长依次调整参数，遍历每一种参数的组合，用交叉验证的方法找出精度最高的组合，即最优的超参数。

网格搜索适用于三四个（或者更少）的超参数，用户列出一个较小的超参数值域，这些超参数至于的笛卡尔积（排列组合）为一组组超参数。网格搜索算法使用每组超参数训练模型并挑选验证集误差最小的超参数组合。

随机搜索（RandomizedSearchCV）

GridSearchCV需要遍历所有可能参数的组合，在面对大数据集和多参数的情况下，非常耗时。当超参数的数量增长时，网格搜索的计算复杂度会呈现指数增长，这时候则使用随机搜索。

（a）对于搜索范围是distribution的超参数，根据给定的distribution随机采样；
（b）对于搜索范围是list的超参数，在给定的list中等概率采样；
（c）对a、b两步中得到的n_iter组采样结果，进行遍历。
注：如果给定的搜索范围均为list，则不放回抽样n_iter次。

　RandomizedSearchCV使用方法和类GridSearchCV 很相似，但他不是尝试所有可能的组合，而是通过选择每一个超参数的一个随机值的特定数量的随机组合，这个方法有两个优点：

• 如果你让随机搜索运行， 比如1000次，它会探索每个超参数的1000个不同的值（而不是像网格搜索那样，只搜索每个超参数的几个值）
• 你可以方便的通过设定搜索次数，控制超参数搜索的计算量。

RandomizedSearchCV的使用方法其实是和GridSearchCV一致的，但它以随机在参数空间中采样的方式代替了GridSearchCV对于参数的网格搜索，在对于有连续变量的参数时，RandomizedSearchCV会将其当做一个分布进行采样进行这是网格搜索做不到的，它的搜索能力取决于设定的n_iter参数，同样的给出代码。

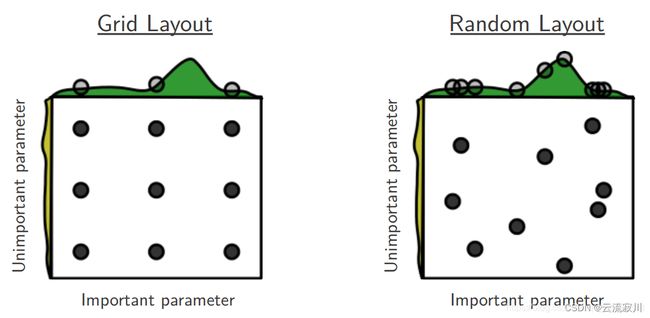
基于上图我们来直观的分析一下随机搜索更加高效的原因：
（a）目标函数为 f(x,y)=g(x)+h(y)，其中绿色为g(x),黄色为h(y)，目的是求f的最大值。
（b）其中由于g(x)数值上要明显大于h(y)，因此有f(x,y)=g(x)+h(y)≈g(x)，也就是说在整体求解f(x,y)最大值的过程中，g(x)的影响明显大于h(y)。
（c）两个图都进行9次实验（搜索），可以看到左图实际探索了各三个点（在横轴和纵轴上的投影均为3个），而右图探索了9个不同的点（横轴纵轴均是，不过实际上横轴影响更大）。
（d）右图更可能找到目标函数的最大值。