广度优先搜索
那么废话讲完了┏ (゜ω゜)=☞
目录
一:认识广搜
广度优先搜索算法的搜索步骤一般是:
二:导入
广度优先搜索一般可以回答两类问题:
三:基础应用
例题1:寻宝(topscoding主题库2638)
例题2:关系网络(topscodin主题库1458)
四:图形类问题:
例题2:细胞
例题3:Satellite Photographs 卫星照片(topscoding主题库2653)
例题4:红与黑(主题库2538)
例5:最少步数(topscoding主题库2587)
一:认识广搜
广度优先搜索BFS(Breadth First Search)也称为宽度优先搜索,它是一种先生成的结点先扩展的策略。
简单来说就是:从一个节点出发,先访问其直接相连的子节点,若子节点不符合,再问其子节点的子节点,按级别顺序依次访问,直到访问到目标节点。
广度优先搜索算法的搜索步骤一般是:
(1)从队列头取出一个结点,检查它按照扩展规则是否能够扩展,如果能则产生一个新结点。(2)检查新生成的结点,看它是否已在队列中存在,如果新结点已经在队列中出现过,就放弃这个结点,然后回到第
(1)步。否则,如果新结点未曾在队列中出现过,则将它加入到队列尾。
(3)检查新结点是否目标结点。如果新结点是目标结点,则搜索成功,程序结束;若新结点不是目标结点,则回到第(1)步,再从队列头取出结点进行扩展。
二:导入
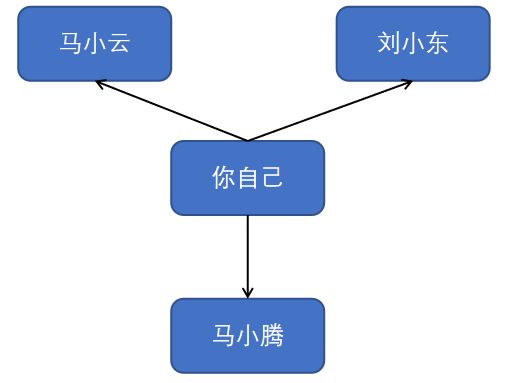
可能对于上面的讲解,同学们还不是很了解什么是广度优先搜索,下面我们通过一个例子再来聊一聊什么是广度优先搜索。假设你自己经营了一家巧克力工厂,你需要找到巧克力销售商,这样你的巧克力才能卖出去。因此,你首先开始在你认识的朋友里面寻找,有没有巧克力销售商。如下图所示,你一共有三个好朋友,分别是马小云、刘小东和马小腾。
一开始的的查找很简单,你只需要创建一个朋友们的名单。然后依次检查名单中的每一个人,看看他是不是巧克力销售商。
首先,你开始查找你的朋友马小云,如果他是巧克力销售商,那么大功告成,查找也就结束了,如果他不是的话继续查找第二个朋友刘小东,同样如果他是巧克力销售商,那么大功告成,查找也就结束了,如果他不是的话继续查找第三个朋友马小腾,如果他是巧克力销售商,那么大功告成,查找也就结束了,如果他不是的话就表示你的朋友里面没有巧克力销售商。那接下来怎么办呢?很显然,接下来你就需要在查找你朋友的朋友有没有巧克力销售商了(是不是有点无脑枚举的意思?)。
同样,你需要首先把朋友的朋友的名单加入列表中,然后再一个个查找他们是否为巧克力销售商。这样一来,你不仅在朋友中查找,还在朋友的朋友中查找。别忘了,你的目标是在你的人际关系网中找到一位巧克力销售商。因此,如果马小腾不是巧克力销售商,就将其朋友也加入到名单中。这意味着你将在她的朋友、朋友的朋友等中查找。使用这种算法将搜遍你的整个人际关系网,直到找到巧克力销售商。这就是广度优先搜索算法。
广度优先搜索一般可以回答两类问题:
第一类问题:从节点A出发,有前往节点B的路径吗?(在你的人际关系网中,有巧克力销售商吗?)
第二类问题:从节点A出发,前往节点B的哪条路径最短?(哪个巧克力销售商与你的关系最近?)刚才你看到了如何回答第一类问题,下面来尝试回答第二类问题——谁是关系最近的巧克力销售商。例如,朋友是一度关系,朋友的朋友是二度关系。
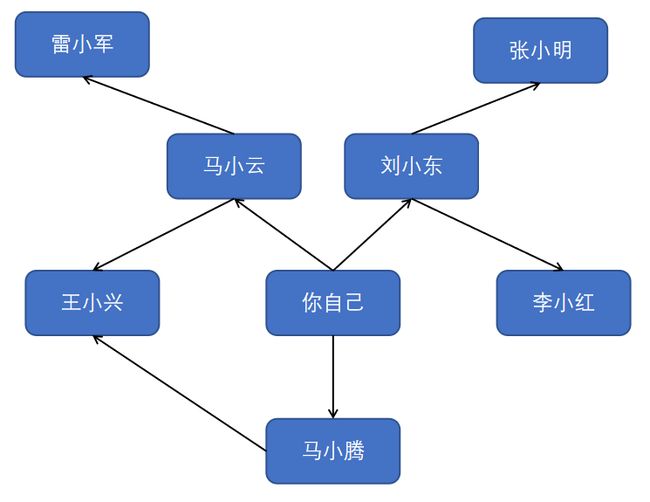
在你看来,一度关系胜过二度关系,二度关系胜过三度关系,以此类推。因此,你应先在一度关系中搜索,确定其中没有巧克力销售商后,才在二度关系中搜索。广度优先搜索就是这样做的!在广度优先搜索的执行过程中,搜索范围从起点开始逐渐向外延伸,即先检查一度关系,再检查二度关系。顺便问一句:将先检查刘小东还是雷小军呢?刘小东是一度关系,而雷小军是二度关系,因此将先检查刘小东,后检查雷小军。你也可以这样看,一度关系在二度关系之前加入查找名单。
你按顺序依次检查名单中的每个人,看看他是否是巧克力销售商。这将先在一度关系中查找,再在二度关系中查找,因此找到的是关系最近的巧克力销售商。广度优先搜索不仅查找从A到B的路径,而且找到的是最短的路径(貌似这里又有一点贪心的感觉了)。
注意,只有按添加顺序查找时,才能实现这样的目的。换句话说,如果马小云先于雷小军加入名单,就需要先检查马小云,再检查雷小军。如果马小云和雷小军都是巧克力销售商,而你先检查雷小军再检查马小云,结果将如何呢?找到的巧克力销售商并非是与你关系最近的,因为雷小军是你朋友的朋友,而马小云是你的朋友。因此,你需要按添加顺序进行检查。有一个可实现这种目的的数据结构,那就是队列(queue),所以这也就是我们之前学习队列知识的原因所在。
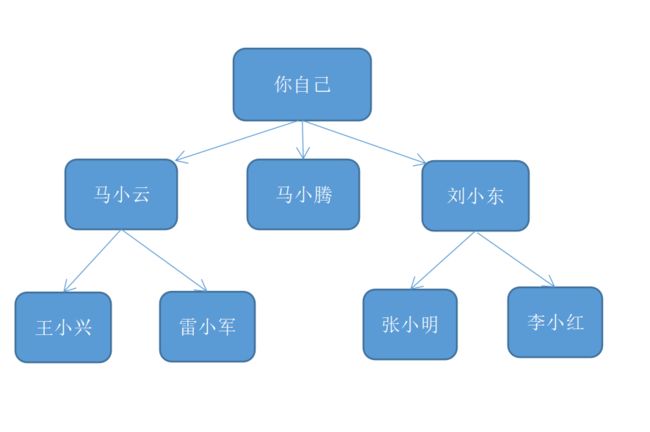
所以,我们可以把上面的查找过程分层,按照层次遍历。每一层遍历完成后,再接着遍历下一层。
三:基础应用
例题1:寻宝(topscoding主题库2638)
小萱萱参加了一个“寻宝”游戏:在一排均匀排列的树上,被随机放置了一个“宝贝”,看谁能以最少的时间找到这个“宝贝”。每一个寻宝的人开始会站在第N(0≤N≤100000)棵树边,假设树有100000 棵,“宝贝”被放在第K(0≤K≤100000)棵树上,寻宝人有两种移动办法:步行和跳跃。假如寻宝人现在在第X棵树边,步行每秒可以从第X棵树向第X-1棵和第X+1棵树走去,跳跃可以让她在1秒内从第X棵树直接跳到第2*X棵树边(假如他有超能力完成跳跃,跳跃过.程中不能超过树的边界)。现在要求找到“宝贝”需要的最短时间。
输入格式:仅有两个整数N和K。
输出格式:最短时间
输入样例:5 17
输出样例: 4
解题思路:首先我们明确这是广度优先搜索的第二类问题,即从节点A出发,前往节点B的哪条路径最短?在本题中即从开始的树n开始,最少需要经过几次就可以找到第k棵树上的宝贝。我们首先从第n棵树出发,对于每一棵树,都有三种方式可以跳到下一棵树,即向前跳一步、向后跳一步和向后2倍距离跳。我们借用样例输入和输出来模拟下这个广度优先搜索的过程。
第1次搜索:5向三个方向搜索,分别是4,6,10;4,6,10进入队列,5出队列
第2次搜索:4向三个方向搜索,分别是3,5,8,去掉5;
6向三个方向搜索,分别是5,7,12,去掉5;
10向三个方向搜索,分别是9,11,20;3,8,7,12,9,11,20进入队列,4,6,10出队列;
第3次搜索:3向三个方向搜索,分别是2,4,6,去掉4和6;
8向三个方向搜索,分别是7,16,9,去掉7和9;7向三个方向搜索,分别是6,8,14,去掉6和8;
12向三个方向搜索,分别是11,13,24,去掉11;9向三个方向搜索,分别是8,10,18,去掉8和10;11向三个方向搜索,分别是10,12,22,去掉10;20向三个方向搜索,分别是19,21,40;2,16,11,13,24,18,12,22,19,21,40进入队列,3,8,7,12,9,11,20出队列;
第4次搜索:2向三个方向搜索,分别是1,3,4,去掉3和4;16向三个方向搜索,分别是15,17,32;
这个时候我们发现已经找到目标节点了,即编号为17的这棵树,并且通过了4次搜索,因此找到“宝贝”需要的最短时间为4次。下面我们一起来用代码来模拟我们上面的这个过程。
整的代码如下所示:
#include
using namespace std;
int t[100001],f[100001]; //数组t存储时间,数组f标记该树有没有跳过
int n,k; //n表示开始位置,k表示结束位置
queueshu; //定义队列shu
int bfs()
{
shu.push(n); //开始位置存入队列中
t[n]=0,f[n]=1; //一开始的时间为0,开始位置被标记为1
while(shu.empty()!=1) //当队列非空时开始循环
{
int x=shu.front(); //x为队列的队首元素
if(x==k){return t[x];} //如果队首等于结束位置,则表示找到了,返回时间
//如果没找到,分三种情况讨论,分别向前跳、向后跳和2倍向后跳
if(x-1>=0&&f[x-1]==0) //如果x-1>=0即可以向前跳,且前面这个树还没有去过
{
shu.push(x-1); //x-1进入队列
t[x-1]=t[x]+1; //时间加1
f[x-1]=1; //x-1被标记
}
if(x+1<=100000&&f[x+1]==0) //如果x+1<=100000即可以向后跳,且后面这个树还没有去过
{
shu.push(x+1); //x+1进队列
t[x+1]=t[x]+1; //时间加1
f[x+1]=1; //x+1被标记
}
if(x*2<=100000&&f[x*2]==0) //如果x*2<=100000即可以向后2倍跳,且后面这个树还没有去过
{
shu.push(x*2); //x*2进队列
t[x*2]=t[x]+1; //时间加1
f[x*2]=1; //x*2被标记
}
shu.pop(); //这个数已经被遍历完了,出队列
}
}
int main()
{
cin>>n>>k;
cout< 例题2:关系网络(topscodin主题库1458)
有n个人,他们的编号为1~n,其中有一些人相互认识,现在x想要认识y,可以通过他所认识的人来认识更多的人(如果a认识b,b认识c,那么a可以通过b来认识c),求出 x 最少需要通过多少人才能认识y。
样例输入:第1行3个整数n、x、y,2≤n≤100,1<=x,y<=n;
接下来的n行是一个 n × n的邻接矩阵,a[i][j]=1 表示 i 认识 j,a[i][j]=0表示不认识。保证i=j时,a[i][j]=0,并且a[i][j]=a[j][i]。
样例输出:一行一个整数,表示 x 认识 y 最少需要通过的人数。数据保证x一定能认识y。
样例输入:
5 1 5
0 1 0 0 0
1 0 1 1 0
0 1 0 1 0
0 1 1 0 1
0 0 0 1 0
样例输出:
2解题思路:首先我们明确这是广度优先搜索的第二类问题,即从节点A出发,前往节点B的哪条路径最短?结合本题样例输入5,1,5,第一个5表示接下来是一个5*5的矩阵,1表示从第1个开始,5表示第5个人结束。首先,1进入队列,搜索1认识的人,显然1只认识2。2入队列,1出队列。接着开始搜索2认识的人,由矩阵可知,2认识1,3,4,其中1已经被标记过了,因此3和4入队列,2出队列;接着开始搜索3认识的人,由矩阵可知,3认识2,4,2,4都已经被标记过了;接着开始搜索4认识的人,由矩阵可知,4认识2,3,5,目标节点5出现,搜索也就结束了。1通过2找到4,再通过4找到5,因此最少需要通过2个人。下面我们一起来用代码来模拟我们上面的这个过程。
完整的代码如下所示:
#include
using namespace std;
int a[101][101],f[101],t[101]; //a数组表示矩阵,f数组标记是否找过,t数组表示通过几个人
int n,x,y; //n表示共有多少人,x表示开始,y表示结束
queuebh; //定义队列 bh
int bfs(int x) //从x节点开始搜索
{
bh.push(x); //x节点入队列
t[x]=0; f[x]=1; //一开始通过0个人认识,把x节点标记为找过
while(bh.empty()!=1) //如果队列非空
{
int i=bh.front(); //队首元素为i
if(i==y){ return t[i]-1;} //如果i==y表示找到了,这个时候即通过了 t[i]-1个人
for(int j=1;j<=n;j++) //如果没有找到,看看这个人认识那些人
{
if(a[i][j]==1&&f[j]==0) // a[i][j]==1表示认识并且这个人没找过
{
bh.push(j); //把它认识的人放进队列
t[j]=t[i]+1; //t的值加1
f[j]=1; //这个人被标记成1
}
}
bh.pop(); //当前这个人已经搜索完了,出队列
}
}
int main()
{
cin>>n>>x>>y;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
cin>>a[i][j];
}
}
cout< 四:图形类问题:
例子:从一个 n * m的迷宫的左上角走到右下角,其中“.”表示该点能走通,“#”表示该点不能走通。要求按照右、下、左、上的方向遍历,请问:利用广搜思路,画出左上角走到右下角的遍历过程?
例题1:快乐的马里奥
https://www.topscoding.com/p/2948
注:此题为topscoding题目
按照广搜的顺序依次填写数字
#include
using namespace std;
int f[110][110];
queuex,y;
int n,m,num=1;
void bfs(int h,int l){
x.push(h),y.push(l);
f[h][l]=1;
while(!x.empty()){
int tx=x.front(),ty=y.front()+1;//向右移动
if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&f[tx][ty]==0){
x.push(tx),y.push(ty);
num++;
f[tx][ty]=num;
}
tx=x.front()+1,ty=y.front();//向下移动
if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&f[tx][ty]==0){
x.push(tx),y.push(ty);
num++;
f[tx][ty]=num;
}
tx=x.front(),ty=y.front()-1;//向左移动
if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&f[tx][ty]==0){
x.push(tx),y.push(ty);
num++;
f[tx][ty]=num;
}
tx=x.front()-1,ty=y.front();//向上移动
if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&f[tx][ty]==0){
x.push(tx),y.push(ty);
num++;
f[tx][ty]=num;
}
x.pop();
y.pop();
}
}
int main(){
cin >> n >> m;
bfs(1,1);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cout << f[i][j]<< " ";
}
cout << endl;
}
return 0;
}
优化后:使用方向数组
#include
using namespace std;
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
int f[110][110];
queuex,y;
int n,m,num=1;
void bfs(int h,int l){
x.push(h),y.push(l);
f[h][l]=1;
while(!x.empty()){
for(int i=0;i<4;i++){
int tx=x.front()+dx[i],ty=y.front()+dy[i];
if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&f[tx][ty]==0){
x.push(tx),y.push(ty);
num++;
f[tx][ty]=num;
}
}
x.pop();
y.pop();
}
}
int main(){
cin >> n >> m;
bfs(1,1);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cout << f[i][j]<< " ";
}
cout << endl;
}
return 0;
}
例题2:细胞
一矩形阵列由数字0到9组成,数字1到9代表细胞,细胞的定义为沿细胞数字上下左右还是细胞数字则为同一细胞,求给定矩形阵列的细胞个数。如阵列:
0234500067
1034560500
2045600671
0000000089
有4个细胞。
输入格式:整数m,n(m行,n列)矩阵(m和n均不超过100)
输出格式:一个数字,表示细胞的个数。
样例输入:
4 10
0234500067
1034560500
2045600671
0000000089
样例输出:
4解题思路:可能很多同学一拿到题目,对于样例的输出4都非常困惑,因此我们首先得弄明白题目的意思,为何输出的结果为4。题目里面说,细胞的定义为沿细胞数字上下左右还是细胞数字则为同一细胞,因此我们对于样例输入第一行的2来说,首先第一行的2345和第二行的3456以及第三行的456组成了同一个细胞,这就是第一个细胞。接着第一行的67是同一个细胞,这是第二个细胞。接着第二行的1和第三行的2是同一个细胞,这是第三个细胞。最后,第二行的5和第三行的671以及第四行的89是同一个细胞,这是第四个细胞。综上所述,一共有4个细胞。那么如何利用代码找到这些细胞呢?首先我们输入这个矩形阵列,对于其中的非零元素开始搜索,搜索分为上下左右四个方向,如果下一个节点非0,则接着对这个点的上下左右进行搜索,并且把这个点标记为0,最后所有节点都为0,则这个搜索完成了,我们也找到了第一个细胞。接着,我们开始查找矩阵中下一个非零元素,开始搜索,每一个完整的搜索就代表一个细胞,因此搜索的总次数也就是细胞的个数。
完整的代码如下:
#include
using namespace std;
char f[101][101]; //为什么用char类型?
//样例输入的不是一个数字而是一串串的数字,无法用int类型
queuex,y; //声明两个队列x和y
//题目中说该细胞的上下左右,假设该细胞的位置为(i,j),
//则这个细胞的上一个为(i-1,j);下一个为(i+1,j);左一个为(i,j-1);右一个为(i,j+1);
//因此上下左右四个方向可以表示成下面两个数组,方便计算
int dx[4]={-1,1,0,0},dy[4]={0,0,-1,1};
int m,n,num; //m表示行,n表示列
void bfs(int h,int l) //h(行),l(列)表示起始值下标
{
x.push(h); y.push(l); //h和l入队列
f[h][l]='0'; //(h,l)赋值为0
while(x.empty()!=1)
{
for(int i=0;i<=3;i++) //循环4个方向
{
int sx=x.front()+dx[i],sy=y.front()+dy[i]; //上下左右四个方向
if(sx>=1&&sx<=m&&sy>=1&&sy<=n&&f[sx][sy]!='0')
//如果x的位置在1到m之间,y的位置在1到n之间,保证不越界,并且该点不是0
{
x.push(sx);y.push(sy);f[sx][sy]='0'; //该点入队列,该点被置为'0'
}
}
x.pop();y.pop(); //队首出队列
}
}
int main()
{
cin>>m>>n;
for (int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
cin>>f[i][j];
}
}
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
if (f[i][j]!='0') //如果是细胞,就把他相连的都变成0
{
bfs(i,j); //从不是0的点(i,j)出发,开始搜索
num++; //完整搜索一次表示有一个细胞
}
}
}
cout< 例题3:Satellite Photographs 卫星照片(topscoding主题库2653)
农场主约翰给他的农场买了W*H像素的卫星照片(1 <= W <= 80, 1 <= H <= 1000),希望找出最大的"连续的"(互相连接的)牧场。对于一个牧场的任何一对像素,其中一个像素如果能横向的或纵向的与属于这个牧场的另一个像素相连,这样的牧场称作是连续的。 (很容易创建形状稀奇古怪的牧场,甚至是围着其它圆圈的圆圈。)
每一张照片都数字化的抽象了,牧场区显示为"*",非牧场区显示为"."。下面是一个10 *5的卫星照片样例:
..*.....**
.**..*****
.*...*....
..****.***
..****.***
这张照片显示了大小分别为4、16、6个像素的连续牧场区。帮助农场主约翰在他的每张卫星照片中找到最大的连续牧场。
输入格式:第 1 行: 两个由空格分开的整数,W 和 H 。第 2 到 H+1 行: 每一行包含 W 个 "*" 或者".",代表卫星照片的横向行。
输出格式:一行为最大连续牧场的大小。
样例输入:
10 5
..*.....**
.**..*****
.*...*....
..****.***
..****.***
样例输出:
16解题思路:我相信同学们一看到这种又是*号又是.的题目就很头疼,其实细心一点的同学早就发现了,这一题跟上一题的细胞很相似。细胞是上下左右,牧场中的像素是横向的或纵向的,所谓横向的或纵向的不就是上下左右吗?细胞这道题目是求有几个细胞,也就是几个连续区域,而我们这道题目是求那个连续区域最大。因此我们只要在每次搜索的时候加一个变量s,没搜索成功一次加1就可以了。然后在求出每次搜索的最大值即最大连续牧场的大小。
完整的代码如下所示:
#include
using namespace std;
char f[1005][85]; //牧场地图
int dx[4]={-1, 0, 1, 0}, dy[4]={0, 1, 0, -1}; //上下左右四个方向
int w,h,maxn; //w示行,h表示列
int bfs(int m,int n) //m,n表示起始值下标 ,int类型
{
queuex,y;
x.push(m); y.push(n); //m和n入队列
f[m][n]='1'; //这个点找过,就标记成字符1
int s=1; //第一个点即s初值为1
while(x.empty()!=1)
{
for(int i=0;i<=3;i++) //循环4个方向
{
int sx=x.front()+dx[i],sy=y.front()+dy[i]; //上下左右四个方向
if(sx>=1&&sx<=h&&sy>=1&&sy<=w&&f[sx][sy]=='*')
//如果x的位置在1到h之间,y的位置在1到w之间,保证不越界,并且该点是*,是连续的牧场
{
x.push(sx);y.push(sy);f[sx][sy]='1'; //该点入队列,该点被置为1表示已经找过了
s++; //找到一个,加1
}
}
x.pop();y.pop(); //队首出队列
}
return s; //每次搜索返回牧场像素的连续个数s
}
int main()
{
cin>>w>>h;
for (int i=1;i<=h;i++) //h和w不要写反了
{
for(int j=1;j<=w;j++)
{
cin>>f[i][j];
}
}
for(int i=1;i<=h;i++)
{
for(int j=1;j<=w;j++)
{
if(f[i][j]=='*') //如果是牧场,就看看它的区域是多大
{
maxn=max(bfs(i, j), maxn); //保留最大值
}
}
}
cout< 例题4:红与黑(主题库2538)
小明站在一个矩形房间里,这个房间的地面铺满了地砖,每块地砖的颜色或是红色或是黑色。小明一开始站在一块黑色地砖上,并且小明从一块地砖可以向上下左右四个方向移动到其他的地砖上,但是他不能移动到红色地砖上,只能移动到黑色地砖上。请你编程计算小明可以走到的黑色地砖最多有多少块。
输入格式:输入包含多组测试数据。每组输入首先是两个正整数W和H,分别表示地砖的列行数。(1<=W,H<=20)。接下来H行,每行包含W个字符,字符含义如下:‘.’表示黑地砖;‘#’表示红地砖;‘@’表示小明一开始站的位置,此位置是一块黑地砖,并且这个字符在每组输入中仅会出现一个。当W=0,H=0时,输入结束。
输出格式:对于每组输入,输出小明可以走到的黑色地砖最多有多少块,包括小明最开始站的那块黑色地砖。
6 9
....#.
.....#
......
......
......
......
......
#@...#
.#..#.
11 9
.#.........
.#.#######.
.#.#.....#.
.#.#.###.#.
.#.#..@#.#.
.#.#####.#.
.#.......#.
.#########.
...........
11 6
..#..#..#..
..#..#..#..
..#..#..###
..#..#..#@.
..#..#..#..
..#..#..#..
7 7
..#.#..
..#.#..
###.###
...@...
###.###
..#.#..
..#.#..
0 0
样例输出:
45
59
6
13
解题思路:我相信很多同学一看到这个题目就放弃了,因为这个样例太奇怪了,其实只要静下心来稍微看一看,就发现其实这道题目跟上面一道卫星的题目很相似。只不过是‘*’和‘.’变成了‘.’和‘#’号了。因此两道题目的解题思路完全一致,只不过本道题是多行测试数据而已,因此我们只要在之前代码的基础上稍作修改就可以了。
完整的代码如下所示:
#include
using namespace std;
char f[21][21];
int dx[4]={-1, 0, 1, 0}, dy[4]={0, 1, 0, -1}; //上下左右四个方向
int w,h,b,c;
queuex,y;
int bfs(int m,int n){
x.push(m); y.push(n); //m和n入队列
int s=1; //第一个点即s初值为1
f[m][n]='#';
while(x.empty()!=1)
{
for(int i=0;i<=3;i++) //循环4个方向
{
int sx=x.front()+dx[i],sy=y.front()+dy[i]; //上下左右四个方向
if(sx>=1&&sx<=h&&sy>=1&&sy<=w&&f[sx][sy]=='.')
{
x.push(sx);y.push(sy);f[sx][sy]='#';
s++; //找到一个,加1
}
}
x.pop();y.pop(); //队首出队列
}
return s;
}
int main(){
while(1){
cin>>w>>h;
if(w==0&&h==0) return 0;
//memset(f,'#',sizeof(f));
for(int i=1;i<=h;i++)
{
for(int j=1;j<=w;j++)
{
cin>>f[i][j];
if(f[i][j]=='@') //找到一开始的位置
{
b=i,c=j;
}
}
}
cout< 例5:最少步数(topscoding主题库2587)
在各种棋中,棋子的走法总是一定的,如中国象棋中马走“日”。有一位小学生就想如果马能有两种走法将增加其趣味性,因此,他规定马既能按“日”走,也能如象一样走“田”字。他的同桌平时喜欢下围棋,知道这件事后觉得很有趣,就想试一试,在一个(100*100)的围棋盘上任选两点A、B,A点放上黑子,B点放上白子,代表两匹马。棋子可以按“日”字走,也可以按“田”字走,俩人一个走黑马,一个走白马。谁用最少的步数走到左上角坐标为(1,1)的点时,谁获胜。现在他请你帮忙,给你A、B两点的坐标,想知道两个位置到(1,1)点可能的最少步数。
输入格式:两行,每行两个正整数,表示马所在的坐标。
输出格式:两行,所走的最少步数。
样例输入:
12 16
18 10
样例输出:
8
9
解题思路:做过几道广搜的题目之后,同学们肯定有点感觉了。对于这道题目,很显然对于每个棋子有很多种走法,在不越界且未走过的基础上搜索。我们先在草稿纸上看看,一共有多少种走法,很显然一共有12种走法。至于具体的代码,我想同学们应该可以独立完成了。
完整的代码如下所示:
解法一:
#include
using namespace std;
int di[13]={0,-2,-2,-1,1,2,2,2,2,1,-1,-2,-2}, //一共12个方向
dj[13]={0,1,2,2,2,2,1,-1,-1,-2,-2,-2,-1};
int c[105][105];
bool f[105][105]; //标记是否走过
int bfs(int x, int y)
{
queueqx, qy;
qx.push(x),qy.push(y);
memset(c,0,sizeof(c));
memset(f,0,sizeof(f)); //清零?为什么
f[x][y]=1,c[x][y]=0; //标记该点走过,第一个点为0步
if(x==1&&y==1) return 0;
while(!qx.empty())
{
for(int i=1;i<=12;i++)
{
int a=qx.front()+di[i], b=qy.front()+dj[i];
if(a>=1&&b>=1&&a<=100&&b<=100&&f[a][b]==0) //未越界,未走过
{
c[a][b]=c[qx.front()][qy.front()]+1; //步数加1
qx.push(a),qy.push(b); //如果没有到终点,就开始搜索,入队列
f[a][b]=1; //标记走过了
if(a==1&&b==1) return c[qx.front()][qy.front()]+1; //也可以return c[a][b]或者 return c[1][1]
}
}
qx.pop(),qy.pop();
}
}
int main()
{
int n1, n2, m1, m2;
cin>>n1>>m1>>n2>>m2;
cout< 解法二:
#include
using namespace std;
bool f[105][105];
int c[105][105];
int dx[13]={0,-2,-2,2,2,-2,-2,-1,1,2,2,-1,1},
dy[13]={0,2,-2,-2,2,1,-1,2,2,1,-1,-2,-2};
int bfs(int h,int l)
{
queue qx,qy;
memset(c,0,sizeof(c));
memset(f,0,sizeof(f));
c[h][l]=0;f[h][l]=1;
qx.push(h);qy.push(l);
while(qx.empty()!=1)
{
for(int i=1;i<=12;i++)
{
int sx=qx.front()+dx[i],sy=qy.front()+dy[i];
if(sx<=100&&sx>=1&&sy<=100&&sy>=1&&f[sx][sy]==0)
{
c[sx][sy]=c[qx.front()][qy.front()]+1;
qx.push(sx);qy.push(sy);
f[sx][sy]=1;
}
if(qx.back()==1&&qy.back()==1){return c[1][1];}
}
qx.pop();qy.pop();
}
}
int main()
{
int a,b,c,d;
cin>>a>>b>>c>>d;
cout< 这期完结了下期见bydy~