深度学习入门——感知机
1 感知机是什么
感知机接收多个输入信号,输出一个信号。这里所说的“信号”可以想象成电流或河流那样具备“流动性”的东西。像电流流过导线,向前方输送电子一样,感知机的信号也会形成流,向前方输送信息。但是,和实际的电流不同的是,感知机的信号只有“流/不流”(1/0)两种取值。
如下图是是一个接收两个输入信号的感知机的例子。x1、x2是输入信号,y是输出信号,w1、w2是权重(w是weight的首字母)。图中的○称为“神经元”或者“节点”。输入信号被送往神经元时,会被分别乘以固定的权重(w1x1、w2x2)。神经元会计算传送过来的信号的总和,只有当这个总和超过了某个界限值时,才会输出1。这也称为“神经元被激活”。这里将这个界限值称为阈值,用符号θ表示。
用数学公式表示如下:
y = { 0 ( w 1 x 1 + w 2 x 2 ⩽ θ ) 1 ( w 1 x 1 + w 2 x 2 > θ ) y=\left\{\begin{array}{ll} 0 & \left(w_{1} x_{1}+w_{2} x_{2} \leqslant \theta\right) \\ 1 & \left(w_{1} x_{1}+w_{2} x_{2}>\theta\right) \end{array}\right. y={01(w1x1+w2x2⩽θ)(w1x1+w2x2>θ)
感知机的多个输入信号都有各自固有的权重,这些权重发挥着控制各个信号的重要性的作用。也就是说,权重越大,对应该权重的信号的重要性就越高。
2 简单逻辑电路与感知机实现
2.1 与门
与门仅在两个输入均为1时输出1,其他时候则输出0。如下真值表:
| a | b | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
下面考虑用感知机来实现这个与门。只需要确定能满足真值表的 w 1 、 w 2 、 θ w_{1}、w_{2}、\theta w1、w2、θ的值,这样的值有无数种,比如 ( w 1 , w 2 , θ ) = ( 0.5 , 0.5 , 0.7 ) (w_{1},w_{2},\theta)=(0.5,0.5,0.7) (w1,w2,θ)=(0.5,0.5,0.7)时,或者者(1.0,1.0,1.0)时,同样也满足与门的条件。
将 θ \theta θ换成 − b -b −b,可以得到含义完全相同的公式, b b b称为偏置, w 1 , w 2 w_{1},w_{2} w1,w2称为权重,公式如下:
y = { 0 ( w 1 x 1 + w 2 x 2 + b ⩽ 0 ) 1 ( w 1 x 1 + w 2 x 2 + b > 0 ) y=\left\{\begin{array}{ll} 0 & \left(w_{1} x_{1}+w_{2} x_{2} + b \leqslant 0\right) \\ 1 & \left(w_{1} x_{1}+w_{2} x_{2} + b>0\right) \end{array}\right. y={01(w1x1+w2x2+b⩽0)(w1x1+w2x2+b>0)
然后,使用python来实现刚才的逻辑电路。定义一个接收两个参数的AND函数。在函数内初始化参数 w 1 、 w 2 、 b w_{1}、w_{2}、b w1、w2、b,当输入的加权总和超过阈值时返回1,否则返回0。程序如下:
import numpy as np
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = AND(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
2.2 或门
或门仅在两个输入均为0时输出0,其他时候均为1.如下真值表:
| a | b | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
下面考虑用感知机来实现这个或门。同样只需要确定能满足真值表的 1、2、 的值,这样的值也有无数种,比如 (1,2,)=(0.5,0.5,0.3) 时,满足或门的条件。
import numpy as np
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.3
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = OR(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
2.2.3 与非门
与非门仅在两个输入均为1时输出0,其他时候均为1,跟与门正好相反。如下真值表:
| a | b | y |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
下面考虑用感知机来实现这个或门。同样只需要确定能满足真值表的 1、2、 的值,这样的值也有无数种,比如 (1,2,)=(-0.5,-0.5,-0.7) 时,满足与非门的条件。
import numpy as np
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = NAND(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
4 感知机的局限性
使用感知机可以实现与门、与非门、或门三种逻辑电路。现在我们来考虑一下异或门(XOR gate)。如下真值表:
| a | b | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
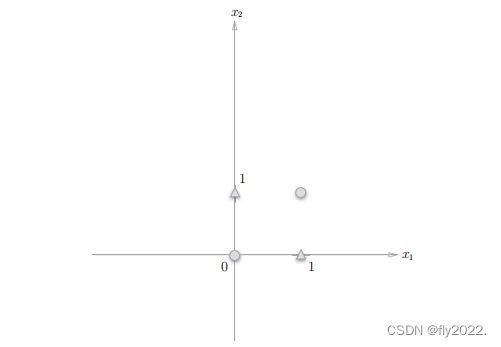
当我们尝试用前面感知机去实现异或门,无论参数设为多少,都不可能实现,试着用前面的实现来找原因,对或门动作可视化可以发现,感知机会生成由直线−0.5 + x1 + x2 = 0分割开的两个空间。其中一个空间输出1,另一个空间输出0,如下图所示:
或门在(0,0)时输出为0,其他输出为1,○表示0,△表示1。如果想制作或门,需要用直线将○和△分开,而这样的直线有无数种,如图上即为一种,那么,换成异或门,能否做出一条直接这样分开呢,显然不存在这样的直线将如下图中的○和△分开
感知机的局限性就在于它只能表示由一条直线分割的空间。由直线分割而成的空间称为线性空间,而由曲线分割而成的空间称为非线性空间,为了实现异或门,上述的感知机无法实现分割,不过可以通过叠加感知机,以实现对非线性空间的处理,这样的感知机称为多层感知机。
5 多层感知机
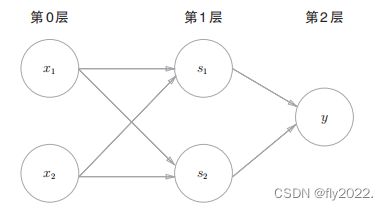
我们知道异或门可以通过组合与门,与非门,或门来实现,如下图:
把s1作为与非门的输出,把s2作为或门的输出上图对应的真值表如下:
| x 1 x_{1} x1 | x 2 x_{2} x2 | s 1 s_{1} s1 | s 2 s_{2} s2 | y |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
使用之前的AND函数,NAND函数,OR函数就可以实现异或XOR函数了。
import numpy as np
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = XOR(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
与门、或门是单层感知机,而异或门是2层感知机。叠加了多层的感知机也称为多层感知机(multi-layered perceptron)。
如上图所示的2层感知机中,先在第0层和第1层的神经元之间进行信号的传送和接收,然后在第1层和第2层之间进行信号的传送和接收。
2.6 从与非门到计算机
多层感知机可以实现比之前见到的电路更复杂的电路。比如,进行加法运算的加法器也可以用感知机实现。此外,将二进制转换为十进制的编码器、满足某些条件就输出1的电路(用于等价检验的电路)等也可以用感知机表示。实际上,使用感知机甚至可以表示计算机!
计算机是处理信息的机器。向计算机中输入一些信息后,它会按照某种既定的方法进行处理,然后输出结果。所谓“按照某种既定的方法进行处理”是指,计算机和感知机一样,也有输入和输出,会按照某个既定的规则进行计算。
人们一般会认为计算机内部进行的处理非常复杂,而令人惊讶的是,实际上只需要通过与非门的组合,就能再现计算机进行的处理。这一令人吃惊的事实说明了什么呢?说明使用感知机也可以表示计算机。前面也介绍了,与非门可以使用感知机实现。也就是说,如果通过组合与非门可以实现计算机的话,那么通过组合感知机也可以表示计算机(感知机的组合可以通过叠加了多层的单层感知机来表示)。