回溯算法之广度优先遍历

目录

迷宫问题

N叉树的层序遍历

 腐烂的橘子

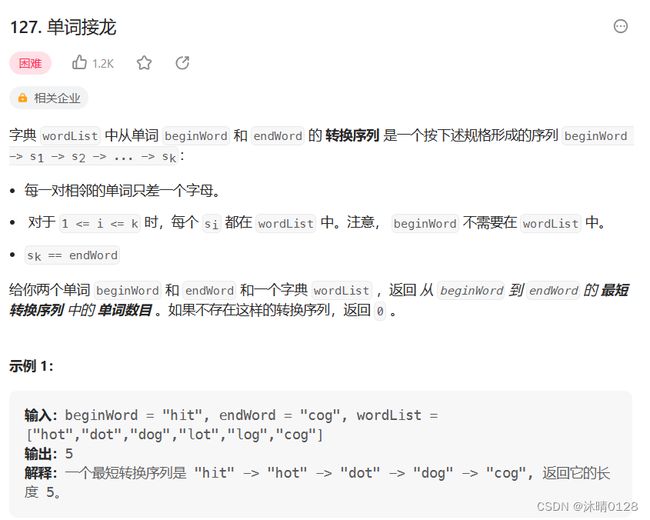
单词接龙

 最小基因变化

 打开转盘锁

---

迷宫问题

假设有一个迷宫，里面有障碍物，迷宫用二维矩阵表示，标记为0的地方表示可以通过，标记为1的地方表示障碍物，不能通过。现在给一个迷宫出口，让你判断是否可以从入口进来之后，走出迷宫，每次可以向任意方向走。

步骤:

1.创建

        1.创建队列

        2.创建book

        3.创建方向矩阵

2.开始位置

        1.开始位置标记遍历过

        2.把开始坐标放到队列中

3.遍历队列

        1.得到队首元素

        2.如果和出口元素相同,范湖true

        3.搜索新的位置

                1.得到位置

                2.判断位置是否合法

                3.如果没有遍历过是通路-->放入队列,标记为1

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

/**
 * @author KYF
 * @create 2023-06-03
 */
class pair{
    public int x;
    public int y;
    public pair(int x,int y){
        this.x=x;
        this.y=y;
    }
}
//0可以通过,1有障碍
public class Test {

     public static boolean dfs(int[][] mat,int startx,int starty,int endx,int endy){
         //队列保存搜索到的位置
         Queue posQ=new LinkedList<>();
         posQ.offer(new pair(startx,starty));
         int row=mat.length;
         int col=mat[0].length;
         int[][] book=new int[row][col];
          book[startx][starty]=1;
          posQ.offer(new pair(startx,starty));
         int[][] next={{0,1},{0,-1},{-1,0},{1,0}};
          //搜索  -->要把队列中的所有元素都搜索完
         while(!posQ.isEmpty()){
             pair curPos=posQ.poll();
             if(curPos.x==endx && curPos.y==endy)
                 return true;
             //搜索新的位置
             for (int i = 0; i < 4; i++) {
                 int nx=curPos.x+next[i][0];
                 int ny=curPos.y+next[i][1];

                 if(nx<0 || nx>=row || ny<0 || ny>=col){
                     continue;
                 }
                 //保存新的位置
                 if(book[nx][ny]==0  && mat[nx][ny]==0){
                     posQ.offer(new pair(nx,ny));
                     book[nx][ny]=1;
                 }
             }
         }
         return false;

     }

    public static void main(String[] args) {
        int[][] mat= {{0, 0, 1, 0},
                      {1, 0, 0, 1},
                       {0,0,0,0},
                       {1,1,0,0}
        };
        while(true){
            System.out.println("输入开始位置和结束位置");
            Scanner sc=new Scanner(System.in);
            int startx=sc.nextInt();
            int starty=sc.nextInt();
            int endx=sc.nextInt();
            int endy=sc.nextInt();
            boolean a=dfs(mat,startx,starty,endx,endy);
            System.out.println(a);
        }

     }
}

N叉树的层序遍历

思路:创建链表和队列,遍历队列,把队列元素取出,值放入链表中,把元素的孩子放到对列中

步骤:

        1.创建队列  和链表

        2.把root结点放入队列

        3.遍历队列

                1.得到队列长度

                2.取出全部元素,一个一个遍历

                3.创建链表,把结点放入链表

                4.把结点的孩子放入队列中

        4.把新的链表存入大链表中

class Solution {
     public List> levelOrder(Node root) {
        List> list=new ArrayList<>();
        Queue q=new LinkedList<>();
        if(root==null){
            return list;
        }
        q.offer(root);
        while(!q.isEmpty()){
            int size=q.size();
            List newL=new ArrayList();
            while(size--!=0){
                Node cur=q.poll();
                newL.add(cur.val);
                for(Node n:cur.children){
                    q.offer(n);
                }
                
            }
            list.add(newL);
        }
        return list;
    }
}

 腐烂的橘子

•  创建队列,用于深度遍历
• 找到所有腐烂的(值为2),放入队列中
• 创建step,用于记录步数
• 遍历队列,直到队列为0,结束
  • 定义flag,用于记录是否当前是否蔓延到新的橘子
  • 得到当前队列的个数,保证当前这次的元素能全部遍历到
    • flag=1  说明有新的被蔓延,放入队列中
    • 遍历四个方向得到新的位置
    • 如果位置不合法或者不是新的橘子,continue
    • flag=1,当前位置标记为腐烂,放入队列中
  • 如果flag=1(这一层遍历完),step++
• 遍历所以,如果还有新鲜橘子则返回-1
• 返回step

class pair{
    int x;
    int y;
    public pair(int x,int y){
        this.x=x;
        this.y=y;
    }
  
}
class Solution {
    public int orangesRotting(int[][] grid) {
        int row=grid.length;
        int col=grid[0].length;
        int[][] next={{0,1},{0,-1},{1,0},{-1,0}};
        Queue q=new LinkedList<>();
        for(int i=0;i=row || ny<0 || ny>=col || grid[nx][ny]!=1){
                        continue;
                    }
                    flag=1;
                    grid[nx][ny]=2;
                    q.offer(new pair(nx,ny));

                }
            }
            if(flag==1){
                step++;
            }
        }

        for(int i=0;i

单词接龙

计数有第一个，开始为1，如果有新的++ 

•  创建两个set,一个存放字典，一个存遍历过的字符串，创建队列用于广度遍历
• 把开始字符串放入队列中
• 遍历队列
  • 得到队列长度，把当前层的都遍历到
    • 得到字符串
    • 如果和结束相等，返回step
    • 遍历字符串的字符分别替换成别的字母
    • 如果在字典中，没有遍历过，放入队列，标记为遍历过
  • step++
• 还没有结束，返回0

  public int ladderLength(String beginWord, String endWord, List wordList) {
        int step=1;//开始不包含在字典中
        Set book=new HashSet<>();
        Set dict=new HashSet<>();
        for(String str:wordList){
            dict.add(str);
        }
        Queue q=new LinkedList<>();
        q.offer(beginWord);
        while(!q.isEmpty()){
            int n=q.size();
            while(n--!=0){
                String cur=q.poll();
                if(cur.contains(endWord)){
                    return step;
                }
                for(int i=0;i

 最小基因变化

 计数没有算第一个，开始为0，如果有新的在++

•  创建两个set,一个存放字典，一个存遍历过的字符串，创建队列用于广度遍历
• step==0
• 把开始字符串放入队列中
• 遍历队列
  • 得到队列长度，把当前层的都遍历到
    • 得到字符串
    • 如果和结束相等，返回step
    • 遍历字符串的字符分别替换成别的字母
    • 如果在字典中，没有遍历过，放入队列，标记为遍历过
  • step++
• 还没有结束，返回0

public int minMutation(String startGene, String endGene, String[] bank) {
       int step=0;
       Set book=new HashSet<>();
       Set dict=new HashSet<>();
       Queue q=new LinkedList<>();
       q.offer(startGene);
       for(String s:bank){
           dict.add(s);
       }
       char[] ch={'A','C','G','T'};
         while(!q.isEmpty()){
           int size=q.size();
           while(size--!=0){
               String cur=q.poll();
               if(cur.contains(endGene)){
                              return step;
                            }
               for(int i=0;i

 打开转盘锁

 

1. 创建
   1. step=0 记录步数  计数没有包含第一个
   2. queue存放数据
   3. set book(是否遍历过) dead(存放死亡字符串)
2. 把开始位置放入队列,和book中
3. deadends放入dead中
4. 遍历队列
   1. 得到队列长度,保证都遍历到
      1. 取出队首字符串
      2. 如果和目标数字相同,则返回步数
      3. 遍历字符串,每一个字符串的每个字符
      4. 两个int型变量记录当前位置,分别表示向上波动和向下波动
      5. 向上:如果是9.-->0,不是++ 向下:如果是0-->9,不是--
      6. 创建两个stringbuilder.把对应位置换掉
      7. 如果不和任何一个相同,没有遍历过
      8. 放入队列,book中
   2. step++
5. return 0

 public int openLock(String[] deadends, String target) {
     //计数没有包含第一个
     int step=0;
     Set book=new HashSet<>();
        Set dead=new HashSet<>();
        for(String str:deadends){
            dead.add(str);
        }
        if(dead.contains("0000")){
            return -1;
        }
        Queue q=new LinkedList<>();
        q.offer("0000");
        book.add("0000");
        while(!q.isEmpty()){
            int size=q.size();
            while(size--!=0){
                String cur=q.poll();
                if(cur.contains(target)){
                    return step;
                }
                //转动
                for(int i=0;i<4;i++){
                    char new1=cur.charAt(i);
                    char new2=cur.charAt(i);

                    //往上转
                    if(new1=='9'){
                        new1='0';
                    }else{
                        new1++;
                    }
                    //往下转
                    if(new2=='0'){
                        new2='9';
                    }else{
                        new2--;
                    }

                    //替换
                    StringBuilder str1=new StringBuilder(cur);
                    StringBuilder str2=new StringBuilder(cur);

                    str1.setCharAt(i,new1);
                    str2.setCharAt(i,new2);

                    String s1=str1.toString();
                    String s2=str2.toString();

                    //判断
                    if(!dead.contains(s1) && !book.contains(s1)){
                        q.offer(s1);
                        book.add(s1);
                    } 
                    if(!dead.contains(s2) && !book.contains(s2)){
                        q.offer(s2);
                        book.add(s2);
                    }

                }
}
         step++;
        }
        return -1;
    }