数学模型——人口增长模型（基于python）

常用人口增长模型

        如果已知今年人口为，年增长率为r，一般使用公式这是在增长率r保持不变的情况下做出的，但实际上，不可能不变，而且还有其他影响因素。说白了，这只是一个预测模型，需要我们考虑到会影响变量的各种因素去优化已有模型。

人口增长模型的建立

一、初始模型

        当我们试图考察一个国家或地区的人口随着时间延续而变化的规律时，就可以利用微积分，将人口看作是连续时间t的连续可微函数x(t)，记初始时刻（t=0）时的人口为，假设单位时间人口增长率为常数r，rx(t)就是单位时间内x(t)的增长量。得到微分方程

易得出，此时，当r>0，人口将呈指数增长，这个模型也被称为Malthus人口模型。

        那么，如何用python去解这样一个微分方程呢？首先，我们设置初值，时间t为0，对应的人口为6.0496（单位：百万）使用python的scipy库进行求解，用matplotlib库进行展示。

from scipy.integrate import odeint
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd


data = pd.read_csv('data.csv')  # 导入数据

'''人口指数增长模型'''
# 初级模型:dx/dt=rx,x(0)=x0（初始时刻）,x(t)表示t时刻下的人口
def expbase(x,t):
    r = 0.2020  # 把人口增长率看做常数
    return np.array(r*x+0*t)

t = np.arange(0,25,1)  # 设置时间序列
a = odeint(expbase,6.4096,t)  # 设置初始值x0为6.4096
plt.plot(a)
plt.scatter(data['t'],data['x'],c='r')
plt.show()

      这里的r和是通过data里的数据，使用参数估计得出来的，常用的就是最小二乘估计，可以利用已知的数据来获取，不过需要我们先把微分方程换成线性方程形式

        观察结果，可以发现，在短期内，对人口增长的预测还是比较准确的，但人口不会一直指数增长，所以在时间后，就可以发现已经明显偏离，故需要对模型进行进一步优化。

二、对增长率进行改进的增长模型

        结合实际，把r视为t的函数r(t)，假设（为什么要设置成这种形式，实际上需要我们对已有数据进行分析进行判断）。所以，此时的指数增长模型为

     利用已知数据，使用最小二乘法估计出此时。

def change(x,t):
    r = 0.3252
    R = 0.0114
    return np.array(r-R*t)*x

T = np.arange(0,30,1)
x = odeint(change,3.9,T)
plt.scatter(data['t'],data['x'],c='r')
plt.plot(x)
plt.show()

        此时，通过观察纵坐标的上限对比一二可以发现，精度确实比较高了一点（当然纵轴区间都一致），在人口预测上，已经较为拟合（当然使用不同的参数估计方法，得出不一样的值，或许可以更好的估计）。但是这还不够，指数增长模型不能进行长期的预测，而且影响人口增长率的因素有很多，需要知道阻滞作用较大的因素。

三、logistic模型

        可以注意到，自然资源，环境因素对人口的阻滞影响较大，而且，人口越大，阻滞作用越大，此时，指数增长模型就不适用了，对于长期的预测，使用logistic模型。为此，设置最大人口数，当达到资源与环境所能容纳的最大人口时，人口数量不会再增长。

        设置r随人口增长而下降的减函数，令x=0时的增长率为r，即r(0)=r=a，当达到最大人口时，，故此时。易得此时的微分方程为

      通过以往数据和非线性最小二乘法估计得出

      代码如下：

def logistic(x,t):
    r = 0.2155
    max_x = 443.9931
    return np.array(r*x*(1-(x/max_x))+0*t)

time = np.arange(0,30,1)
y = odeint(logistic,7.6962,time)
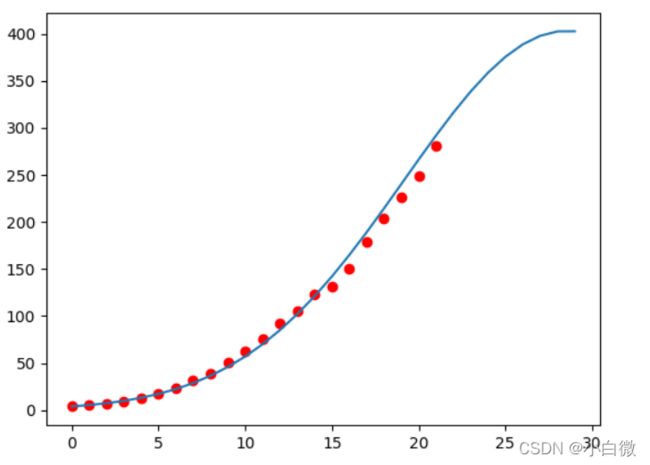
plt.scatter(data['t'],data['x'],c='r')
plt.plot(y)
plt.show()

         对比一二，就可以发现，此时的预测就较为符合现实，logistic模型比指数增长模型作到更好的预测，适用于长期的预测。

         至于其他影响因素，需要我们查询相关文献资料，来探索，当然，并非影响因素越多越好，总会出现一些意料之外的事。

        其中，关于模型参数的来源，可在【续】数学模型——人口增长模型中给出，以及数据，感谢支持。【更新于2023年3月24日】

        本篇完结！