最短路之Dijkstra算法——以不同城市之间的距离为例（基于python）

        首先，非常感谢b站up主对于Dijkstra算法的介绍，受益匪浅，关于这个算法的视频链接在这[Python学习]实现迪杰斯特拉算法并生成最短路径。我也是跟着这位up主才算慢慢懂了这个算法的具体情况。下面，本文就关于Dijksta算法进行相关解释以及python代码实现和案例分析。

目录

一、背景

二、 代码及解释

三、 第三方库解决方法

四、 案例——设备更新问题

五、 总结

---

一、背景

        最短路算法不仅可以解决任意两个地点之间的最短路径，还可以解决诸如管道铺设、线路安全、工厂布局、设备更新等问题。

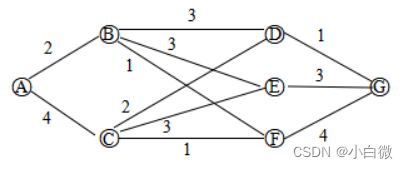
        这里就不讲关于图论的一些东西，讲起来有点复杂，在能理解本文的基础上，给大家先说一下如何去理解下面这个图

        可以看到，图上有些点是直接连接的，有些是没有。对于直连的，如A到B，线上有标注2，即为A到B的距离，但对于A到C，这种没有直接连接的点，记它的距离为无穷大。节点即图上的点。本文使用的例图为无向图，即表示可以从A到B，也可以从B到A。对于有向图的即表示只能顺着箭头方向走，不能往回走，距离也就为无穷大。

        本文主要讲最短路算法中的Dijksta算法，它适用于路权非负的情况。具体步骤简化理解大概就是（个人理解，如有误，欢迎大佬批评指正）：

        1.先确定起始点，起始点与起始点之间的距离为0

        2.确定终点，找出起始点能到达终点的全部路径

        3.通过迭代，找出起始点到终点的最短距离，并对它进行标记

        乍一看，很简单，然而，并不然，如果起始点与终点之间存在很多中间点时，就很难通过人工计算。下面，通过python去实现诸如上述三个步骤。

二、 代码及解释

       以上图为例子， 我们输入的矩阵就是network，也就是常说的邻接矩阵，这个矩阵为方阵。第一行第一列的数据为A到自A的距离。但里面的零并不一定表示自己到自己的距离，例如第一行第五列，表示A到E是没有直连的，这可能跟我上面说的无穷有些矛盾，不过算法真正运行的不是这个矩阵，所以先不用管。仔细观察，可以发现这个矩阵是对称的，当然，也仅限于无向图。

        定义函数，s为起始点，d为终点

        path是一个空列表，用于储存从某点到某点的最短路径，从这里看出s到d的最短路径需要经过哪些点。

        n为节点个数。

        对于fmax，引用numpy库中的inf，意味无穷大。

        w为构造的与输入矩阵network同样维数的0矩阵，用于算法运行。

        book为一个列表，元素个数为节点数，它的作用是，当已经确定某点到某点的最小距离时，进行标记，若有其他路径包括这条路径，即可减少程序的计算。

        dis为最终返回的路径列表，表示从某点到某点的最小路径，一共有n个。

        minpath存储某点到某点的中会经过的节点。path中的节点由它决定。

import numpy as np


network = np.array([[0,2,4,0,0,0,0],
                 [2,0,0,3,3,1,0],
                 [4,0,0,2,3,1,0],
                 [0,3,2,0,0,0,1],
                 [0,3,3,0,0,0,3],
                 [0,1,1,0,0,0,4],
                 [0,0,0,1,3,4,0]])

def Dijkstra(network,s,d):  # 迪杰斯特拉算法算s到t的最短路径，并返回该路径和距离
    print("Start Dijstra Path……")
    path = []  # 储存s到d的最短路径
    n = len(network)  # 节点个数
    fmax = np.inf
    w = [[0 for i in range(n)] for j in range(n)]
    book = [0 for i in range(n)]  # 是否已经是最小的标记列表
    dis = [fmax for i in range(n)]  # s到其他节点的最小距离
    book[s-1] = 1  # 节点编号从1开始，列表序号从0开始
    midpath = [-1 for i in range(n)]  # 上一跳列表

---

         这一步就是将w矩阵初始化，变成程序能够处理的标准矩阵，处理后的w中直连或者本身为fmax。对于i=s-1，其实是因为列表的序号是从0开始的，而我们习惯是从1开始

'''这个循环把原矩阵中的0标价为fmax，且认为直连就是最短（但事实并非如此）'''
    for i in range(n):
        for j in range(n):
            if network[i][j] != 0:
                w[i][j] = network[i][j]  # 0→max
            else:
                w[i][j] = fmax

            if i == s-1 and network[i][j] != 0:  # 直连的节点最小距离就是network[i][j]
                dis[j] = network[i][j]

---

        接下来就是算法的主体部分，n-1次循环就是除了s的节点外的其他节点，for循环中第一个min是会不断更新的，直到找到最短距离，它的作用即在下方的if判断中，检查是不是距离是不是小于min，如果是的话，对min进行更新，否则用u进行记录，标记出已经找出最小路径的点。dis最初的元素全为fmax，通过迭代更新其中的元素，此时通过这个for循环得到的还不是最小的，要在经过下一个循环。不过，最终得到的都是最小路径。例如dis输出为[inf, 2, 4, 5, 5, 3, 6]，即表示从第一个点出发，依次到各个点的最小距离。

        下一个以v为元素遍历的for循环中，这一步用于比较直连是否是最短，如果不是，则换其他的，同时对minpath列表进行更新。此时最短距离已经更新完毕，接下来是得到路径。

        j=d-1的解释和上面的i一样，都是由于习惯不同。

 '''算法主体'''
    for i in range(n-1):  # n-1次遍历，除了s节点
        min = fmax  # min的值是一直变化的
        for j in range(n):
            if book[j] == 0 and dis[j] < min:  # 如果未遍历且距离最小，反复比较得出最短距离
                min = dis[j]
                u = j
        book[u] = 1  # 标记已到达的节点
        # u处于一个循环体内，从2到7遍历
        for v in range(1,n):  # u直连的节点遍历一遍
            '''关键步骤，用于比较与此节点直连的节点的长度'''
            if dis[v] > dis[u] + w[u][v]:
                dis[v] = dis[u] + w[u][v]
                midpath[v] = u+1  # 上一跳更新
    j = d-1  # j是序号
    path.append(d)  # 因为存储的是上一跳，所以先加入目的节点d，最后倒置

---

        在此循环中，只是s到d的最短路径，并不包括其他点之间。

        对于后面那个reverse方法，从上面path添加d就可以知道，需要转置，要不然就是反的

 while midpath[j] != -1:
        path.append(midpath[j])
        j = midpath[j]-1
    path.append(s)
    path.reverse()  # 倒置列表
    print('path:',path)
    print(dis)

        至此，算法也就完成了，接下来，调用这个函数就行，试验用A到G的最短路，即1到7.

Dijkstra(network,1,7)

        结果表示，从A到G的最短距离为6，路径为A—B—D—G。整个算法想要完整理解还是稍微有点困难（大佬避开嘿嘿），大家可以反复观看以下，以下给出完整得代码，便于观察。

import numpy as np


def Dijkstra(network,s,d):  # 迪杰斯特拉算法算s到t的最短路径，并返回该路径和代价
    print("Start Dijstra Path……")
    path = []  # 储存s到t的最短路径
    n = len(network)  # 节点个数
    fmax = np.inf
    w = [[0 for i in range(n)] for j in range(n)]
    book = [0 for i in range(n)]  # 是否已经是最小的标记列表
    dis = [fmax for i in range(n)]  # s到其他节点的最小距离
    book[s-1] = 1  # 节点编号从1开始，列表序号从0开始
    midpath = [-1 for i in range(n)]  # 上一跳列表

    # 此步可以省略，只要输入矩阵规范就可
    '''这个循环把原矩阵中的0标价为fmax，且认为直连就是最短（但事实并非如此）'''
    for i in range(n):
        for j in range(n):
            if network[i][j] != 0:
                w[i][j] = network[i][j]  # 0→max
            else:
                w[i][j] = fmax

            if i == s-1 and network[i][j] != 0:  # 直连的节点最小距离就是network[i][j]
                dis[j] = network[i][j]

    # print('dis:',dis)
    '''算法主体'''
    for i in range(n-1):  # n-1次遍历，除了s节点
        min = fmax  # min的值是一直变化的
        for j in range(n):
            if book[j] == 0 and dis[j] < min:  # 如果未遍历且距离最小，反复比较得出最短距离
                min = dis[j]
                u = j
        # print('book:',book)
        book[u] = 1  # 标记已到达的节点
        # print('u:',u)
        # print('dis:',dis)
        # u处于一个循环体内，从2到7遍历
        for v in range(1,n):  # u直连的节点遍历一遍
            '''关键步骤，用于比较与此节点直连的节点的长度'''
            if dis[v] > dis[u] + w[u][v]:
                dis[v] = dis[u] + w[u][v]
                midpath[v] = u+1  # 上一跳更新
    j = d-1  # j是序号
    path.append(d)  # 因为存储的是上一跳，所以先加入目的节点d，最后倒置

    while midpath[j] != -1:
        path.append(midpath[j])
        j = midpath[j]-1
    path.append(s)
    path.reverse()  # 倒置列表
    print('path:',path)
    print(midpath)
    print(dis)

network = np.array([[0,2,4,0,0,0,0],
                 [2,0,0,3,3,1,0],
                 [4,0,0,2,3,1,0],
                 [0,3,2,0,0,0,1],
                 [0,3,3,0,0,0,3],
                 [0,1,1,0,0,0,4],
                 [0,0,0,1,3,4,0]])
Dijkstra(network,1,7)

三、 第三方库解决方法

        如果大家实在看不懂上面的代码，但又想用这个方法，这边给出了第三方库的解决方案，使用networkx库，由于对这个库了解不是很深，目前我只知道这个库可以画这类图，以及用Dijkstra算法求最短路，最大流问题。接下来就用代码，跟大家介绍以下这个方法

import networkx as nx

dis = [(0,1,2),(0,2,4),(1,3,3),(1,4,3),(1,5,1),(2,3,2),(2,4,3),(2,5,1),(3,6,1),
       (4,6,3),(5,6,4)]
g = nx.Graph()
g.add_weighted_edges_from(dis)
a = nx.to_numpy_matrix(g,nodelist=range(7))
p = nx.dijkstra_path(g,source=0,target=6,weight='weight')
d = nx.dijkstra_path_length(g,0,6,weight='weight')
print('最短路径为p={},最短距离为d={}'.format(p,d))

        同样是用上面的例子，但是对比之下，代码就少了很多。简单介绍一下。

        第一个dis是一个列表，（0，1，2）表示从A到B的距离为2，，以此类推。

        g为初始化一个图，Graph表示生成无向图。

        接下来为图添加节点和路权，参数为dis

        a对应生成的邻接矩阵。

        p使用Dijkstra算法得到最短路径，d得到最短距离。

         可以看出，和上面的代码算法得到结果一致，不过要看那个p列表，可以全部元素＋1，即和上面的代码运行结果一致。

四、 案例——设备更新问题

        接下来用一道题实践一下，虽然跟直接说某点到某点之间的最短路径不同，但是本质是一样的。不过这题我也只是试了一下，不一定保证对，所以大家可以思考一下，希望能对大家有所启发。

        某企业在今后5年内需使用一台机器，该种机器的每年购置费和维修费（与机器的役龄有关）如下表所示。试制定机器购置和更新计划，使5年内的成本最小。

年份	1	2	3	4	5
购置费 维修费	11 5	11 6	12 8	12 11	13 18

        我的想法是这样的：

        令表示第i年初买进用到第j-1年末中所包含的所有费用，此时wij即包含第i年买进时的购置费和j-i年的维修费用，故可知

        用networkx库画出对应的图，如下所示：

         最终用代码解得，第一年买进用到第三年，然后在第三年买入用到第五年末，可使费用最低，为53单位。下面为代码

import networkx as nx
import numpy as np
import pylab as plt


dis = [(1,5,41),(1,4,30),(1,3,22),(1,2,16),(1,6,59),(2,3,16),
       (2,4,23),(2,5,30),(2,6,41),(3,4,17),(3,5,23),(3,6,31),
       (4,5,17),(4,6,28),(5,6,18)]
g = nx.DiGraph()
g.add_nodes_from(range(1,7))
g.add_weighted_edges_from(dis)
pos = nx.shell_layout(g)
w = nx.get_edge_attributes(g,'weight')
nx.draw(g,pos,with_labels=True,font_weight='bold',font_size=12)
nx.draw_networkx_edge_labels(g,pos,edge_labels=w)
plt.show()
a = nx.to_numpy_matrix(g,nodelist=range(1,7))
p = nx.dijkstra_path(g,source=1,target=6,weight='weight')
d = nx.dijkstra_path_length(g,1,6,weight='weight')
print(p,d,sep='\n')

        g.add_nodes_from表示增加节点，g.add_weighted_edges_from表示增加路权，参数位dis，pos为作图的一个参数，代码从w开始到plt.show都是为作图环节（如不需要，可以忽略）。接下来和上面示例一致，用Dijkstra算法解决。

五、 总结

        使用算法一步一步算还是比较困难的，所谓算法就是给人想的，程序是代码想的，关键就是如何让电脑理解你的想法，不过这个Dijkstra算法有现成的库还是比较方便的，当然也不要只是局限于求某点到某点的最短距离，可以引申一下，达到真正理解。

        算法，还是需要多练。对于上面的代码和算法的解释，如果有错误的地方，欢迎各位大神批评指正。有不懂的地方，也可以评论区或者直接私信我。

        创作不易，谢谢点赞——收藏——关注！！！