代码随想录刷题——二叉搜索树专题篇
博主个人博客网站:文客
这个系列主要记录着对于代码随想录上面题目的题解和理解
如果你想每天和我一起刷题,可以关注一下我的个人博客网站:文客,我会每天在这里更新技术文章和面试题,也会及时收到大家的评论与留言,欢迎各位大佬来交流!
700.二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
示例 1:
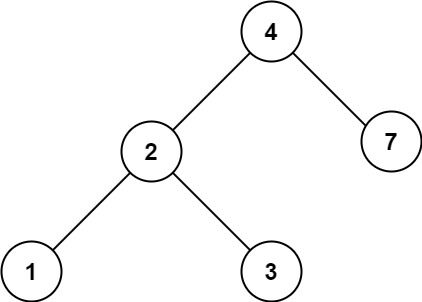
输入:root = [4,2,7,1,3], val = 2
输出:[2,1,3]
Example 2:
输入:root = [4,2,7,1,3], val = 5
输出:[]
提示:
数中节点数在 [1, 5000] 范围内
1 <= Node.val <= 107
root 是二叉搜索树
1 <= val <= 107
思路:
根据二叉搜索树的特点,如果val比当前节点小,那就向左搜索,如果val比当前节点大那就向右搜索,复杂度O(logn)
题解:
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
if(root == null){
return null;
}
if(root.val == val){
return root;
}
if(root.val > val){
return searchBST(root.left,val);
}else if(root.val < val){
return searchBST(root.right,val);
} else {
return root;
}
}
}
98.验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:root = [2,1,3]
输出:true
示例 2:
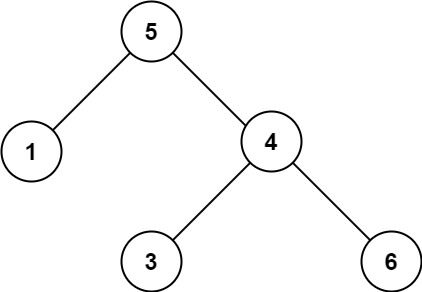
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
- 树中节点数目范围在
[1, 104]内 -2^31 <= Node.val <= 2^31 - 1
思路:
注意Node.val的数值范围,我们选用long来存储前一个节点的数据,因为二叉搜索树中序遍历就是一个升序的数组,只要满足中序遍历时当前节点大于前一个节点就是二叉搜索树了,复杂度O(n)
题解:
class Solution {
long pre = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
if(root == null){
return true;
}
boolean leftValid = isValidBST(root.left);
if(root.val <= pre){
return false;
}
pre = root.val;
boolean rightValid = isValidBST(root.right);
return leftValid && rightValid;
}
}
530.二叉搜索树的最小绝对差
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。
示例 1:
输入:root = [4,2,6,1,3]
输出:1
示例 2:
输入:root = [1,0,48,null,null,12,49]
输出:1
思路:
这道题和验证二叉搜索树差不多,只是多了一个做差的操作。
题解:
class Solution {
int pre = -1;
int res = Integer.MAX_VALUE;
public int getMinimumDifference(TreeNode root) {
if(root == null){
return 0;
}
traversal(root);
return res;
}
public void traversal(TreeNode root){
if(root == null){
return;
}
traversal(root.left);
if(pre >= 0){
res = Math.min(res,root.val - pre);
}
pre = root.val;
traversal(root.right);
}
}
235.二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
思路:
这道题我的解法是和236二叉树的最近公共祖先解法一样,实在没有想到怎么应用二叉搜索树的特性,采用的方法就是后续遍历节点,递归函数的返回值是TreeNode类型,我们定义两个左右节点来接收左右子树的返回值,那么返回值如何定义呢?如果找到与p、q相等的节点,则返回当前节点。然后根据左右节点接收到的情况来判断祖先。
题解:
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null){
return null;
}
if(root == p || root == q){
return root;
}
TreeNode leftNode = lowestCommonAncestor(root.left,p,q);
TreeNode rightNode = lowestCommonAncestor(root.right,p,q);
if(leftNode == null && rightNode == null){
return null;
} else if(leftNode != null && rightNode == null){
return leftNode;
} else if(leftNode == null && rightNode != null){
return rightNode;
} else {
return root;
}
}
}
701.二叉搜索树中的插入操作
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例 1:
输入:root = [4,2,7,1,3], val = 5
输出:[4,2,7,1,3,5]
示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25
输出:[40,20,60,10,30,50,70,null,null,25]
示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出:[4,2,7,1,3,5]
思路:
根据当前节点的值与val之间的关系来判断递归的方向,然后用root.left或者root.right来接住新加入的节点
题解:
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if(root == null){
return new TreeNode(val);
}
if(root.val > val){
root.left = insertIntoBST(root.left,val);
}
if(root.val < val){
root.right = insertIntoBST(root.right,val);
}
return root;
}
}
450.删除二叉搜索树中的节点
思路:
按照二叉搜索树的特性,可以很快地寻找到要删除的节点,注意的是删除节点时左右子树如何处理
题解:
题解一:
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if(root == null){
return null;
}
if(root.val == key){
if(root.left == null){
return root.right;
}
if(root.right == null){
return root.left;
}
TreeNode cur = root.right;
while(cur.left != null){
cur = cur.left;
}
cur.left = root.left;
root = root.right;
}
if(root.val > key){
root.left = deleteNode(root.left,key);
}
if(root.val < key){
root.right = deleteNode(root.right,key);
}
return root;
}
}
题解二:
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if(root == null){
return null;
}
if(root.val > key){
root.left = deleteNode(root.left,key);
} else if(root.val < key){
root.right = deleteNode(root.right,key);
} else {
if(root.left == null){
return root.right;
}
if(root.right == null){
return root.left;
}
TreeNode cur = root.right;
while(cur.left != null){
cur = cur.left;
}
cur.left = root.left;
root = root.right;
return root;
}
return root;
}
}
669.修剪二叉搜索树
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
示例 1:
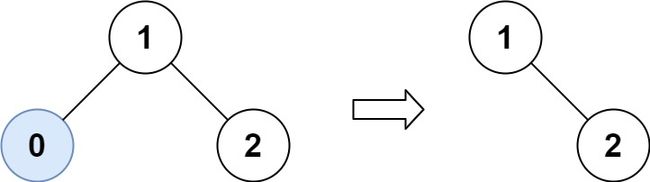
输入:root = [1,0,2], low = 1, high = 2
输出:[1,null,2]
示例 2:
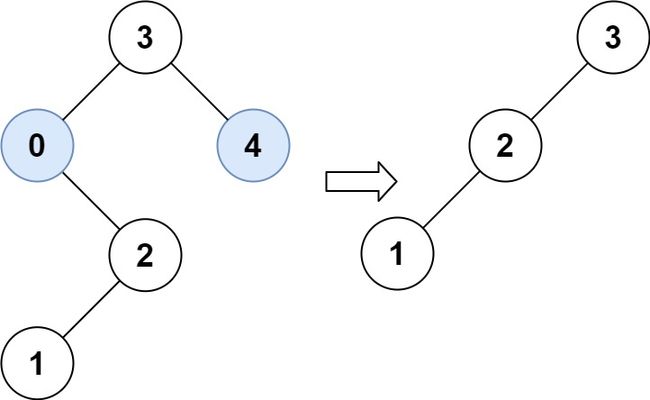
输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出:[3,2,null,1]
题解:
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
if(root == null){
return null;
}
if(root.val < low){
return trimBST(root.right,low,high);
} else if(root.val > high){
return trimBST(root.left,low,high);
} else {
root.left = trimBST(root.left,low,high);
root.right = trimBST(root.right,low,high);
}
return root;
}
}
108.将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
示例 1:
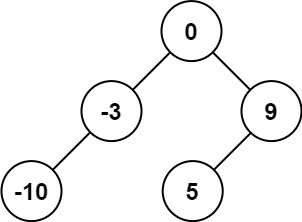
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:
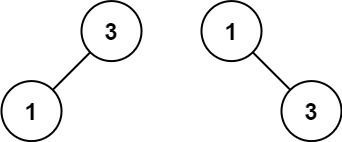
输入:nums = [1,3]
输出:[3,1]
解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
思路:
切割数组,每个数组的中值就是根节点,然后递归构建树,题目中说要求高度平衡,其实用这种方式所构建的树一定是平衡的
题解:
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return build(nums,0,nums.length);
}
public TreeNode build(int[] nums, int left, int right){
if(left >= right){
return null;
}
int mid = left + ((right - left) >> 1);
TreeNode root = new TreeNode(nums[mid]);
root.left = build(nums,left,mid);
root.right = build(nums,mid + 1,right);
return root;
}
}
538.将二叉搜索树转换为累加树
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
示例 1:
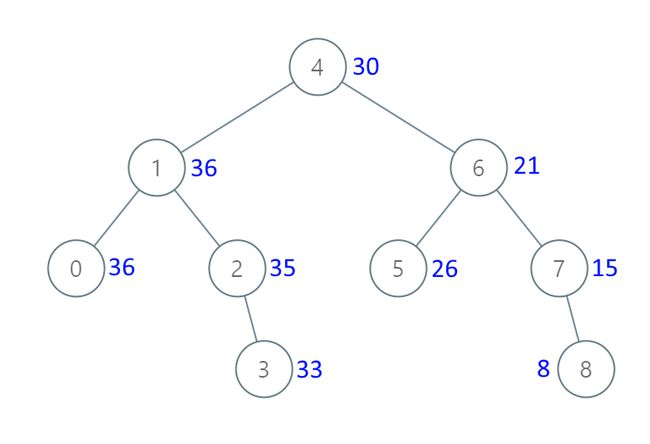
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1]
输出:[1,null,1]
示例 3:
输入:root = [1,0,2]
输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1]
输出:[7,9,4,10]
思路:
这道题主要是想好遍历的顺序,题目要求更新每个节点的值为大于等于当前节点的值的累加和,那么大于等于该节点的值从哪里寻找呢?根据二叉搜索树的特性,当然是从右树中寻找了。我们平时常用根左右、左根右、左右根这三种遍历方式,这道题应该用右根左的遍历方式,你自己捋一遍就门清了
题解:
class Solution {
int sum = 0;
public TreeNode convertBST(TreeNode root) {
if(root == null){
return null;
}
convertBST(root.right);
sum += root.val;
root.val = sum;
convertBST(root.left);
return root;
}
}
示例 4:
输入:root = [3,2,4,1]
输出:[7,9,4,10]
思路:
这道题主要是想好遍历的顺序,题目要求更新每个节点的值为大于等于当前节点的值的累加和,那么大于等于该节点的值从哪里寻找呢?根据二叉搜索树的特性,当然是从右树中寻找了。我们平时常用根左右、左根右、左右根这三种遍历方式,这道题应该用右根左的遍历方式,你自己捋一遍就门清了
题解:
class Solution {
int sum = 0;
public TreeNode convertBST(TreeNode root) {
if(root == null){
return null;
}
convertBST(root.right);
sum += root.val;
root.val = sum;
convertBST(root.left);
return root;
}
}