电信保温杯

电信保温杯笔记——代码随想录刷题攻略二叉树

电信保温杯笔记——代码随想录刷题攻略
1.关于二叉树，你该了解这些！
- 二叉树代码
- 测试代码
2.二叉树：一入递归深似海，从此offer是路人
- 144.二叉树的前序遍历
- - 方式一：递归
- 94.二叉树的中序遍历
- - 方式一：递归
- 145.二叉树的后序遍历
- - 方式一：递归
3.二叉树：听说递归能做的，栈也能做！
- 144.二叉树的前序遍历
- - 方式二：非递归（栈）非统一法
- 94.二叉树的中序遍历
- - 方式二：非递归（栈）非统一法
  - - 原方法
    - 修改
- 145.二叉树的后序遍历
- - 方式二：非递归（栈）非统一法
  - - 原方法
    - 修改
4.二叉树：前中后序迭代方式的写法就不能统一一下么？
- 144.二叉树的前序遍历
- - 方式三：非递归（栈）统一法
- 94.二叉树的中序遍历
- - 方式三：非递归（栈）统一法
- 145.二叉树的后序遍历
- - 方式三：非递归（栈）统一法
5.二叉树：层序遍历登场！
- 102.二叉树的层序遍历
- - 方式一：递归
  - - 使用层数作为变量
    - 使用深度作为变量
  - 方式二：非递归（队列）非统一写法
  - 方式三：非递归（队列）统一写法
- 补充题目
6.二叉树：你真的会翻转二叉树么？
- 226.翻转二叉树
- - 方式一：递归
  - 方式二：非递归（栈）非统一法
7.本周小结！（二叉树）
8.二叉树：我对称么？
- 101. 对称二叉树
- - 方式一：递归
  - 方式二：非递归（单向队列）
- 补充题目
9.二叉树：看看这些树的最大深度
- 104.二叉树的最大深度
- - 方式一：递归
  - - 使用层数作为变量
    - 使用高度作为变量
  - 方式二：非递归
- 补充题目
10.二叉树：看看这些树的最小深度
- 111.二叉树的最小深度
- - 方式一：递归
  - 方式二：非递归
11.二叉树：我有多少个节点？
- 222.完全二叉树的节点个数
- - 方式一：递归
  - 方式二：非递归
12.二叉树：我平衡么？
- 110.平衡二叉树
- - 方式一：递归
  - - 使用辅助类Result
    - 不使用辅助类：
  - 方法二：非递归
  - - 暴力迭代法
    - 优化
13.二叉树：找我的所有路径？
- 257. 二叉树的所有路径
- - 方式一：递归
  - 方式二：非递归
14.本周总结！二叉树系列二
15.二叉树：以为使用了递归，其实还隐藏着回溯
16.二叉树：做了这么多题目了，我的左叶子之和是多少？
- 404.左叶子之和
- - 方式一：递归
  - 方式二：非递归
17.二叉树：我的左下角的值是多少？
- 513.找树左下角的值
- - 方式一：递归
  - 方式二：非递归
18.二叉树：路径总和
- 112. 路径总和
- - 方式一：递归
  - 方式二：非递归
- 113. 路径总和 II
20.二叉树：构造一棵最大的二叉树
- 106.从中序与后序遍历序列构造二叉树
- 105.从前序与中序遍历序列构造二叉树
21.本周小结！（二叉树系列三）
22.二叉树：合并两个二叉树
- 617.合并二叉树
- - 方式一：递归
  - - 新建节点
    - 合并才新建节点
  - 方式二：非递归
  - - 合并才新建节点
23.二叉树：二叉搜索树登场！
- 700.二叉搜索树中的搜索
- - 方式一：递归
  - 方式二：非递归
24.二叉树：我是不是一棵二叉搜索树
- 98.验证二叉搜索树
- - 方式一：递归
  - 方式二：非递归
25.二叉树：搜索树的最小绝对差
- 530.二叉搜索树的最小绝对差
- - 方式一：递归
  - 方式二：非递归
26.二叉树：我的众数是多少？
- 501.二叉搜索树中的众数
- - 方式一：递归
  - 方式二：非递归
27.二叉树：公共祖先问题
- 236. 二叉树的最近公共祖先
28.本周小结！（二叉树系列四）
29.二叉树：搜索树的公共祖先问题
- 235. 二叉搜索树的最近公共祖先
- - 方式一：递归
  - 方式二：非递归
30.二叉树：搜索树中的插入操作
- 701.二叉搜索树中的插入操作
- - 方式一：递归
  - 方式二：非递归
31.二叉树：搜索树中的删除操作
- 450.删除二叉搜索树中的节点
32.二叉树：修剪一棵搜索树
- 669. 修剪二叉搜索树
- - 方式一：递归
小结
33.二叉树：构造一棵搜索树
- 108.将有序数组转换为二叉搜索树
- - 方式一：递归
  - 方式二：非递归
34.二叉树：搜索树转成累加树
- 538.把二叉搜索树转换为累加树
- - 方式一：递归
  - 方式二：非递归
35.二叉树：总结篇！（需要掌握的二叉树技能都在这里了）
总结

电信保温杯笔记——代码随想录刷题攻略

代码随想录刷题攻略
电信保温杯笔记——代码随想录刷题攻略

1.关于二叉树，你该了解这些！

讲义地址

二叉树代码

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

测试代码

class Test{
    public static void main(String[] args) {
        TreeNode root = createTree("[2,1,3,null,4,null,7]");
        Solution solution = new Solution();
    }
    
    // string的输入格式为："[2,1,3,null,4,null,7]"
    public static TreeNode createTree(String string){
        if (string.equals("[]")){
            return null;
        }
        ArrayList<Integer> list = new ArrayList<>();
        String temp = "";
        for (int i = 1; i < string.length(); i++) {
            char ch = string.charAt(i);
            if (ch == ',' || ch == ']') {
                if (temp.equals("null")) {
                    // null点先赋值为无穷小，后面再剪枝
                    list.add(Integer.MIN_VALUE);
                }else {
                    list.add(Integer.valueOf(temp));
                }
                temp = "";
            }else {
                temp += ch;
            }
        }
        if (list.get(0) == Integer.MIN_VALUE){
            return null;
        }
        TreeNode root = new TreeNode();


        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        TreeNode cur;

        for (int i = 0; i < list.size(); i++) {
            cur = queue.poll();
            cur.val = list.get(i);
            // null点先赋值为无穷小，后面再剪枝
            cur.left = new TreeNode(Integer.MIN_VALUE);
            cur.right = new TreeNode(Integer.MIN_VALUE);
            queue.offer(cur.left);
            queue.offer(cur.right);
        }

        // 剪枝，将值为无穷小的子节点删除
        queue.clear();
        queue.offer(root);
        while (!queue.isEmpty()) {
            cur = queue.poll();
            if (cur.left.val == Integer.MIN_VALUE) {
                cur.left = null;
            }else {
                queue.offer(cur.left);
            }
            if (cur.right.val == Integer.MIN_VALUE) {
                cur.right = null;
            }else {
                queue.offer(cur.right);
            }
        }
        return root;
    }
}

2.二叉树：一入递归深似海，从此offer是路人

讲义地址

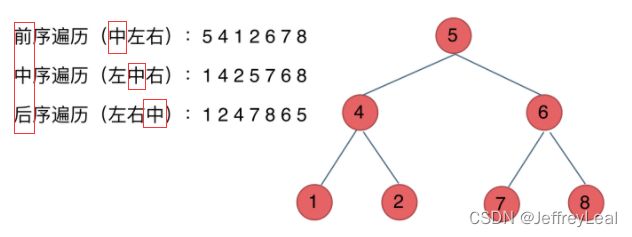
二叉树遍历有前序、中序、后序、层次遍历4种，其中前序、中序、后序的区别在于：左右节点的操作相对次序不变，中节点的操作在左右节点的前中后，就代表前序、中序、后序。

一周刷爆LeetCode，算法da神左神（左程云）耗时100天打造算法与数据结构基础到高级全家桶教程，直击BTAJ等一线大厂必问算法面试题真题详解笔记的P6 5.二叉树中，基础第五课题目一：二叉树节点结构，有讲解先序中序后序遍历的递归与非递归方法。

下面三题的非递归方法在下两章中。

144.二叉树的前序遍历

leetcode地址

方式一：递归

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        preOrderRecurrent(root, res);
        return res;
    }

    public void preOrderRecurrent(TreeNode node, List<Integer> res){
        if (node == null){
            return;
        }
        res.add(node.val);
        preOrderRecurrent(node.left, res);
        preOrderRecurrent(node.right, res);
    }
}

94.二叉树的中序遍历

leetcode地址

方式一：递归

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        inOrderRecurrent(root, res);
        return res;
    }

    public void inOrderRecurrent(TreeNode node, List<Integer> res){
        if (node == null){
            return;
        }
        inOrderRecurrent(node.left, res);
        res.add(node.val);
        inOrderRecurrent(node.right, res);
    }
}

145.二叉树的后序遍历

leetcode地址

方式一：递归

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        postOrderRecurrent(root, res);
        return res;
    }

    public void postOrderRecurrent(TreeNode node, List<Integer> res){
        if (node == null){
            return;
        }
        postOrderRecurrent(node.left, res);
        postOrderRecurrent(node.right, res);
        res.add(node.val);
    }
}

3.二叉树：听说递归能做的，栈也能做！

讲义地址

非递归方法又分为统一法和非统一法。
统一法：先序中序后序的代码结构相同，其中几条代码顺序不同；
非统一法：3者代码风格不能做到统一写法，只有前序和后序是相似的，中序的逻辑与另外两种不同。

统一法在下一章中介绍。

144.二叉树的前序遍历

leetcode地址

方式二：非递归（栈）非统一法

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null){
            return res;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.add(root);
        while (!stack.empty()){
            TreeNode temp = stack.pop();
            res.add(temp.val);
            if (temp.right != null){
                stack.push(temp.right);
            }
            if (temp.left != null){
                stack.push(temp.left);
            }
        }
        return res;
    }
}

94.二叉树的中序遍历

leetcode地址

方式二：非递归（栈）非统一法

原方法

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null){
            return res;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.empty()){
            if (cur != null){
                stack.push(cur);
                cur = cur.left;
            }else{
                cur = stack.pop();
                res.add(cur.val);
                cur = cur.right;
            }
        }
        return res;
    }
}

左节点需要遍历到底，才会开始遍历右节点，右节点再重复遍历自身左节点的操作。

里面的if-else可以改为while

修改

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) {
            return res;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.empty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            cur = stack.pop();
            res.add(cur.val);
            cur = cur.right;
        }
        return res;
    }
}

145.二叉树的后序遍历

leetcode地址

方式二：非递归（栈）非统一法

原方法

这是先序遍历的基础上修改，将先序变成中右左，然后再倒序得到的，并不是真正的后序遍历。

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null){
            return res;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.empty()){
            TreeNode temp = stack.pop();
            res.add(temp.val);
            if (temp.left != null){
                // 放入左节点
                stack.push(temp.left);
            }
            if (temp.right != null){
                // 放入右节点
                stack.push(temp.right);
            }
        }
        Collections.reverse(res);
        return res;
    }
}

如果不使用reverse操作，可以使用多一个stack来收集val，然后将stack吐出到res即可。

修改

真正的后序遍历。

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null){
            return res;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;// 这个指针用于添加节点
        TreeNode temp = null;// 这个指针用于对stack顶节点进行判断
        TreeNode pre = null;// 这个指针用于判断当前节点右节点是否遍历过
        while (cur != null || !stack.empty()){
            while (cur != null){
                stack.push(cur);
                cur = cur.left;
            }
            temp = stack.peek();
            // 查看当前节点的右节点是否遍历过，null相对于遍历了
            if (temp.right == null || temp.right == pre){
            	// 右节点已经遍历过
                pre =stack.pop();
                res.add(pre.val);
                cur = null;
            }else {
            	//没有遍历过
                cur = temp.right;
            }
        }
        return res;
    }
}

4.二叉树：前中后序迭代方式的写法就不能统一一下么？

讲义地址

非递归（栈）统一法效率低，因为它加入了大量的null记号作为中节点的标记，虽然记一种当三种用，不过效率低，面试意义不大。

这个方法的核心思想：以先序为例，将栈节点弹出，化栈节点为3个节点，将这三个节点压进去栈，顺序是右左中null，弹出顺序就是null中左右，以null为中节点的标记，意思就是中节点的左右子节点已经遍历完了。

144.二叉树的前序遍历

leetcode地址

方式三：非递归（栈）统一法

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null){
            return res;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        TreeNode cur = root.left;
        while (!stack.empty()){
            TreeNode temp = stack.pop();
            if (temp != null){
            	// 由于先序的出栈顺序是中左右，所以入栈顺序是右左中
                if (temp.right != null){
                	// 放入右节点
                    stack.push(temp.right);
                }
                if (temp.left != null){
                	// 放入左节点
                    stack.push(temp.left);
                }
            	// 放入中节点和null，null作为中节点的标记
                stack.push(temp);
                stack.push(null);
            }else {
                temp = stack.pop();
                res.add(temp.val);
            }
        }
        return res;
    }
}

94.二叉树的中序遍历

leetcode地址

方式三：非递归（栈）统一法

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null){
            return res;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        TreeNode cur = root.left;
        while (!stack.empty()){
            TreeNode temp = stack.pop();
            if (temp != null){
            	// 由于中序的出栈顺序是左中右，所以入栈顺序是右中左
                if (temp.right != null){
                	// 放入右节点
                    stack.push(temp.right);
                }
            	// 放入中节点和null，null作为中节点的标记
                stack.push(temp);
                stack.push(null);
                if (temp.left != null){
                	// 放入左节点
                    stack.push(temp.left);
                }
            }else {
                temp = stack.pop();
                res.add(temp.val);
            }
        }
        return res;
    }
}

145.二叉树的后序遍历

leetcode地址

方式三：非递归（栈）统一法

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null){
            return res;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        TreeNode cur = root.left;
        while (!stack.empty()){
            TreeNode temp = stack.pop();
            if (temp != null){
            	// 由于后序的出栈顺序是左右中，所以入栈顺序是中右左
            	// 放入中节点和null，null作为中节点的标记
                stack.push(temp);
                stack.push(null);
                if (temp.right != null){
                	// 放入右节点
                    stack.push(temp.right);
                }
                if (temp.left != null){
                	// 放入左节点
                    stack.push(temp.left);
                }
            }else {
                temp = stack.pop();
                res.add(temp.val);
            }
        }
        return res;
    }
}

5.二叉树：层序遍历登场！

讲义地址

层次遍历，实质就是先序遍历。但并不是输出结果的数组拼接起来就是先序遍历的顺序，因为并不是每一层的数组填满了再填下一层的数组。

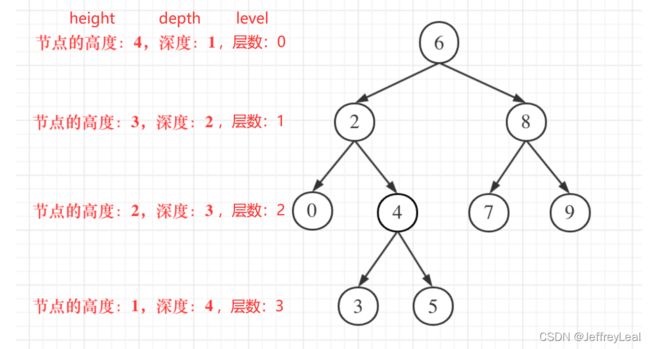
102.二叉树的层序遍历

leetcode地址

方式一：递归

使用层数作为变量

根节点代表第0层。level代表node所在的层。

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        ArrayList res = new ArrayList<>();
        levelOrderRecurrent(root, 0, res);
        return res;
    }

    public void levelOrderRecurrent(TreeNode node, int level, List<List<Integer>> res) {
        if (node == null) {
            return;
        }

        if (res.size() <= level) {
            res.add(new ArrayList<>());
        }
        res.get(level).add(node.val);

        levelOrderRecurrent(node.left, level + 1, res);
        levelOrderRecurrent(node.right, level + 1, res);
        return;
    }
}

使用深度作为变量

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        ArrayList res = new ArrayList<>();
        levelOrderRecurrent(root, 1, res);
        return res;
    }

    public void levelOrderRecurrent(TreeNode node, int depth, List<List<Integer>> res) {
        if (node == null) {
            return;
        }

        if (res.size() < depth) {
            res.add(new ArrayList<>());
        }
        res.get(depth - 1).add(node.val);

        levelOrderRecurrent(node.left, depth + 1, res);
        levelOrderRecurrent(node.right, depth + 1, res);
        return;
    }
}

方式二：非递归（队列）非统一写法

用一个变量len记录该层的长度，也就是当前队列的长度。

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        ArrayList res = new ArrayList<>();
        if (root == null){
            return res;
        }
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        ArrayList<Integer> list = null;
        TreeNode temp = null;
        int len = 0;
        while (!queue.isEmpty()){
            len = queue.size();
            list = new ArrayList<>();
            while (len > 0){
                temp = queue.pop();
                list.add(temp.val);
                if (temp.left != null){
                    queue.add(temp.left);
                }
                if (temp.right != null){
                    queue.add(temp.right);
                }
                len--;
            }
            res.add(list);
        }
        return res;
    }
}

方式三：非递归（队列）统一写法

以null作为该层结尾的标记。

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        ArrayList res = new ArrayList<>();
        if (root == null){
            return res;
        }
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        queue.add(null);
        ArrayList<Integer> list = new ArrayList<>();
        TreeNode temp = null;
        while (!queue.isEmpty()){
            temp = queue.pop();
            if (temp != null){
                list.add(temp.val);
                if (temp.left != null){
                    queue.add(temp.left);
                }
                if (temp.right != null){
                    queue.add(temp.right);
                }
                if (queue.peek() == null){
                    queue.add(null);
                }
            }else {
                if (queue.isEmpty()){
                    break;
                }
                res.add(list);
                list = new ArrayList<Integer>();
            }
        }
        return res;
    }
}

补充题目

107.二叉树的层次遍历II
199.二叉树的右视图
637.二叉树的层平均值
429.N叉树的层序遍历
515.在每个树行中找最大值
116.填充每个节点的下一个右侧节点指针
117.填充每个节点的下一个右侧节点指针II
104.二叉树的最大深度
111.二叉树的最小深度

6.二叉树：你真的会翻转二叉树么？

讲义地址

226.翻转二叉树

leetcode地址

先序后序遍历都可以，也是各有三种方法，无非是先交换还是先遍历，唯独中序不行，不能遍历中穿插交换。

下面是先序的做法。

方式一：递归

class Solution {
    public TreeNode invertTree(TreeNode root) {
        preOrderRecurrentFun(root);
        return root;
    }
    public void preOrderRecurrentFun(TreeNode node){
        if (node == null){
            return;
        }
        TreeNode temp = node.left;
        node.left = node.right;
        node.right = temp;
        preOrderRecurrentFun(node.left);
        preOrderRecurrentFun(node.right);
    }
}

方式二：非递归（栈）非统一法

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null){
            return root;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        TreeNode cur = null;
        TreeNode temp = null;
        while (!stack.empty()){
            cur = stack.pop();
            temp = cur.left;
            cur.left = cur.right;
            cur.right = temp;
            if (cur.right != null){
                stack.push(cur.right);
            }
            if (cur.left != null){
                stack.push(cur.left);
            }
        }
        return root;
    }
}

7.本周小结！（二叉树）

讲义地址

8.二叉树：我对称么？

讲义地址

101. 对称二叉树

leetcode地址

有点像先序遍历。有三种方法。

方式一：递归

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return compare(root.left, root.right);
    }

    private boolean compare(TreeNode left, TreeNode right) {

        if (left == null && right != null) {
            return false;
        }
        if (left != null && right == null) {
            return false;
        }
        if (left == null && right == null) {
            return true;
        }
        if (left.val != right.val) {
            return false;
        }
        // 比较外侧
        boolean compareOutside = compare(left.left, right.right);
        // 比较内侧
        boolean compareInside = compare(left.right, right.left);
        return compareOutside && compareInside;
    }
}

方式二：非递归（单向队列）

class Solution {
    public boolean isSymmetric(TreeNode root) {
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.add(root.left);
        queue.add(root.right);
        TreeNode left = null;
        TreeNode right = null;
        while (!queue.isEmpty()){
            left = queue.pop();
            right = queue.pop();
            if (left == null && right == null){
                continue;
            }
            if (left == null || right == null || right.val != left.val){
                return false;
            }
            queue.add(left.left);
            queue.add(right.right);
            queue.add(left.right);
            queue.add(right.left);
        }
        return true;
    }
}

补充题目

100.相同的树
572.另一个树的子树

9.二叉树：看看这些树的最大深度

讲义地址

104.二叉树的最大深度

leetcode地址

方式一：递归

使用层数作为变量

根节点为第0层，它的子节点为第1层，如此类推，level代表当前层，maxLevel代表遇到的最大层。采用顺序记录的树结构：

class Solution {
    public int maxDepth(TreeNode root) {
        return preOrderRecurrentFun(root, 0, -1) + 1;
    }
    public int preOrderRecurrentFun(TreeNode node, int level, int maxLevel){
        if (node == null){
            return maxLevel;
        }
        maxLevel = Integer.max(level, maxLevel);
        int leftMaxLevel = preOrderRecurrentFun(node.left, level + 1, maxLevel);
        int rightMaxLevel = preOrderRecurrentFun(node.right, level + 1, maxLevel);
        maxLevel =Integer.max(leftMaxLevel, rightMaxLevel);
        return maxLevel;
    }
}

使用高度作为变量

还有逆序记录的树状结构，记录当前节点子树的最大高度height：

class Solution {
    public int maxDepth(TreeNode root) {
        return preOrderRecurrentFun(root);
    }
    public int preOrderRecurrentFun(TreeNode node){
        if (node == null){
            return 0;
        }
        int leftHeight = preOrderRecurrentFun(node.left);
        int rightHeight = preOrderRecurrentFun(node.right);
        return Integer.max(leftHeight, rightHeight) + 1;
    }
}

方式二：非递归

层次遍历

class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null){
            return 0;
        }
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        TreeNode temp = null;
        int depth = 0;
        int len = 0;
        while (!queue.isEmpty()){
            len = queue.size();
            while (len > 0){
                temp = queue.poll();
                if (temp.left != null){
                    queue.offer(temp.left);
                }
                if (temp.right != null){
                    queue.offer(temp.right);
                }
                len--;
            }
            depth++;
        }
        return depth;
    }
}

补充题目

559.n叉树的最大深度

10.二叉树：看看这些树的最小深度

讲义地址

111.二叉树的最小深度

leetcode地址

方式一：递归

后序遍历。

class Solution {
    public int minDepth(TreeNode root) {
        return postOrderRecurrentFun(root);
    }
    public int postOrderRecurrentFun(TreeNode node){
        if (node == null){
            return 0;
        }
        int leftMinDepth = postOrderRecurrentFun(node.left);
        int rightMinDepth = postOrderRecurrentFun(node.right);
        if (leftMinDepth == 0){
            return rightMinDepth + 1;
        }
        if(rightMinDepth == 0){
            return leftMinDepth + 1;
        }
        return Integer.min(leftMinDepth, rightMinDepth) + 1;
    }
}

方式二：非递归

class Solution {
    public int minDepth(TreeNode root) {
        if (root == null){
            return 0;
        }
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int depth = 0;
        TreeNode temp = null;
        int len = 0;
        while (!queue.isEmpty()){
            len = queue.size();
            depth++;
            while (len > 0){
                temp = queue.poll();
                // 碰到叶节点返回
                if (temp.left == null && temp.right == null){
                    return depth;
                }
                if (temp.left != null){
                    queue.offer(temp.left);
                }
                if (temp.right != null){
                    queue.offer(temp.right);
                }
                len--;
            }
        }
        return depth;
    }
}

11.二叉树：我有多少个节点？

讲义地址

222.完全二叉树的节点个数

leetcode地址

方式一：递归

class Solution {
    public int countNodes(TreeNode root) {
        return recurrentFun(root);
    }
    public int recurrentFun(TreeNode node){
        if (node == null){
            return 0;
        }
        return recurrentFun(node.left) + recurrentFun(node.right) + 1;
    }
}

方式二：非递归

层次遍历。

class Solution {
    public int countNodes(TreeNode root) {
        if (root == null){
            return 0;
        }
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int res = 0;
        TreeNode temp = null;
        int len = 0;
        while (!queue.isEmpty()){
            len = queue.size();
            while (len > 0){
                temp = queue.poll();
                res++;
                if (temp.left != null){
                    queue.offer(temp.left);
                }
                if (temp.right != null){
                    queue.offer(temp.right);
                }
                len--;
            }
        }
        return res;
    }
}

12.二叉树：我平衡么？

讲义地址

110.平衡二叉树

leetcode地址

方式一：递归

使用辅助类Result

后序遍历。

class Solution {
    public boolean isBalanced(TreeNode root) {
        return recurrent(root).isBalanced;
    }
    public Result recurrent(TreeNode node){
        Result res = new Result();
        if (node == null){
            return res;
        }
        Result leftRes = recurrent(node.left);
        Result rightRes = recurrent(node.right);
        res.height = Integer.max(leftRes.height, rightRes.height) + 1;
        boolean isBalanced = true;
        if (Math.abs(leftRes.height - rightRes.height) > 1){
            isBalanced = false;
        }
        res.isBalanced = isBalanced && leftRes.isBalanced && rightRes.isBalanced;
        
        return res;
    }
}
class Result{
    int height = 0;
    boolean isBalanced = true;

    public Result() {
    }

    public Result(int height, boolean isBalanced) {
        this.height = height;
        this.isBalanced = isBalanced;
    }
}

不使用辅助类：

其实这个也是后序遍历，只是可以提前返回而已，只要将这行代码

        if (leftHeight == -1) {
            return -1;
        }

下移一行，其实就是后序遍历。

class Solution {
   /**
     * 递归法
     */
    public boolean isBalanced(TreeNode root) {
        return getHeight(root) != -1;
    }

    private int getHeight(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftHeight = getHeight(root.left);
        if (leftHeight == -1) {
            return -1;
        }
        int rightHeight = getHeight(root.right);
        if (rightHeight == -1) {
            return -1;
        }
        // 左右子树高度差大于1，return -1表示已经不是平衡树了
        if (Math.abs(leftHeight - rightHeight) > 1) {
            return -1;
        }
        return Math.max(leftHeight, rightHeight) + 1;
    }
}

方法二：非递归

因为要比较左右节点的高度，所以因为使用真正的后序遍历。

暴力迭代法

class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null){
            return true;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;// 这个指针用于添加节点
        TreeNode temp = null;// 这个指针用于对stack顶节点进行判断
        TreeNode pre = null;// 这个指针用于判断当前节点右节点是否遍历过
        while (cur != null || !stack.empty()){
            while (cur != null){
                stack.push(cur);
                cur = cur.left;
            }
            temp = stack.peek();
            // 查看当前节点的右节点是否遍历过，null相对于遍历了
            if (temp.right == null || temp.right == pre){
                // 右节点已经遍历过
                if (Math.abs(getHeight(temp.left) - getHeight(temp.right)) > 1){
                    return false;
                }
                pre =stack.pop();
                cur = null;
            }else {
                //没有遍历过
                cur = temp.right;
            }
        }
        return true;
    }
    public int getHeight(TreeNode root){
        if (root == null){
            return 0;
        }
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int len;
        int depth = 0;
        TreeNode temp;
        while (!queue.isEmpty()){
            len = queue.size();
            while (len > 0) {
                temp = queue.poll();
                if (temp.left != null){
                    queue.offer(temp.left);
                }
                if (temp.right != null) {
                    queue.offer(temp.right);
                }
                len--;
            }
            depth++;
        }
        return depth;
    }
}

优化

针对暴力迭代法的getHeight方法做优化，利用TreeNode.val来保存当前结点的高度，但个人认为这样会破坏了树本身的值。

13.二叉树：找我的所有路径？

讲义地址

257. 二叉树的所有路径

leetcode地址

方式一：递归

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        ArrayList<String> res = new ArrayList<>();
        recurrent(root, "", res);
        return res;
    }
    public void recurrent(TreeNode node, String path, List<String> res){
        if (node == null){
            return;
        }
        path = path + String.valueOf(node.val);
        recurrent(node.left, path + "->" , res);
        recurrent(node.right, path + "->" , res);
        if (node.left == null && node.right == null){
            res.add(path);
        }
    }
}

方式二：非递归

层次遍历。

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        ArrayList<String> res = new ArrayList<>();
        if (root == null){
            res.add("");
            return res;
        }
        LinkedList<TreeNode> queue = new LinkedList<>();
        ArrayList<String> curPaths;
        ArrayList<String> oldPaths = new ArrayList<>();
        oldPaths.add("");
        queue.offer(root);
        int len;
        TreeNode temp;
        String path;
        while (!queue.isEmpty()){
            len = queue.size();
            curPaths = new ArrayList<>();
            for (int i = 0; i < len; i++) {
                temp = queue.poll();
                path = oldPaths.get(i)+ String.valueOf(temp.val);
                if (temp.left == null && temp.right == null) {
                    res.add(path);
                    continue;
                }
                if (temp.left != null){
                    queue.offer(temp.left);
                    curPaths.add(path + "->");
                }
                if (temp.right != null){
                    queue.offer(temp.right);
                    curPaths.add(path + "->");
                }
            }
            oldPaths = curPaths;
        }
        return res;
    }
}

14.本周总结！二叉树系列二

讲义地址

15.二叉树：以为使用了递归，其实还隐藏着回溯

讲义地址

16.二叉树：做了这么多题目了，我的左叶子之和是多少？

讲义地址

404.左叶子之和

leetcode地址

方式一：递归

和先序后序中序层次遍历无关，主要是遍历的过程中如何判断是左叶子节点。

判断条件：当前点a的左子节点不为空，并且左子节点的左右子节点都为空，那么a的左子节点为左叶节点。

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        return recurrent(root);
    }
    public int recurrent(TreeNode node){
        // level是node的上一层，根节点为0层，根节点的上一层为-1层
        if (node == null) {
            return 0;
        }
        int res = 0;
        if (node.left != null) {
            if (node.left.left == null && node.left.right == null){
                res += node.left.val;
            }
        }
        res += recurrent(node.left);
        res += recurrent(node.right);
        return res;
    }
}

方式二：非递归

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null){
            return 0;
        }
        int res = 0;
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        TreeNode temp;
        while (!stack.empty()) {
            temp = stack.pop();
            if (temp.right != null){
                stack.push(temp.right);
            }
            if (temp.left != null){
                stack.push(temp.left);
                if (temp.left.left == null && temp.left.right == null) {
                    res += temp.left.val;
                }
            }
        }
        return res;
    }
}

17.二叉树：我的左下角的值是多少？

讲义地址

513.找树左下角的值

leetcode地址

方式一：递归

层次遍历。

class Solution {
    public int findBottomLeftValue(TreeNode root) {
        if (root == null){
            return 0;
        }
        ArrayList<List<Integer>> res = new ArrayList<>();
        levelOrderRecurrent(root, 1, res);
        return res.get(res.size() - 1).get(0);
    }

    public void levelOrderRecurrent(TreeNode node, int depth, List<List<Integer>> res) {
        if (node == null) {
            return;
        }

        if (res.size() < depth) {
            res.add(new ArrayList<Integer>());
        }
        res.get(depth - 1).add(node.val);

        levelOrderRecurrent(node.left, depth + 1, res);
        levelOrderRecurrent(node.right, depth + 1, res);
        return;
    }
}

方式二：非递归

层次遍历。

class Solution {
    public int findBottomLeftValue(TreeNode root) {
        if (root == null){
            return 0;
        }
        int res = 0;
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int len;
        TreeNode temp;
        while (!queue.isEmpty()) {
            len = queue.size();
            res = queue.peek().val;
            while (len > 0){
                temp = queue.poll();
                if (temp.left != null){
                    queue.offer(temp.left);
                }
                if (temp.right != null) {
                    queue.offer(temp.right);
                }
                len--;
            }
        }
        return res;
    }
}

18.二叉树：路径总和

讲义地址

112. 路径总和

leetcode地址

方式一：递归

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root == null){
            return false;
        }
        return preOrderRecurrent(root, 0, targetSum);
    }
    public boolean preOrderRecurrent(TreeNode node, int sum, int targetSum){
        sum += node.val;
        if (sum == targetSum && node.left == null && node.right == null) {
            return true;
        }
        boolean b1 = false;
        boolean b2 = false;
        if (node.left != null){
            b1 = preOrderRecurrent(node.left, sum, targetSum);
            // 左子节点已经找到路径了，右节点就不用找了
            if (b1 == true){
                return true;
            }
        }
        if (node.right != null){
            b2 = preOrderRecurrent(node.right, sum, targetSum);
        }
        return b1 || b2;
    }
}

方式二：非递归

层次遍历。

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root == null) {
            return false;
        }
        LinkedList<TreeNode> queue = new LinkedList<>();
        ArrayList<Integer> curSums;
        ArrayList<Integer> oldSums = new ArrayList<>();
        oldSums.add(0);
        queue.offer(root);
        int len;
        int curSum;
        TreeNode temp;
        while (!queue.isEmpty()) {
            len = queue.size();
            curSums = new ArrayList<>();
            for (int i = 0; i < len; i++) {
                temp = queue.poll();
                curSum = oldSums.get(i) + temp.val;
                if (curSum == targetSum && temp.left == null && temp.right == null) {
                    return true;
                }
                // oldSum.get(i) < targetSum
                if (temp.left != null) {
                    queue.offer(temp.left);
                    curSums.add(curSum);
                }
                if (temp.right != null) {
                    queue.offer(temp.right);
                    curSums.add(curSum);
                }
            }
            oldSums = curSums;
        }
        return false;
    }
}

113. 路径总和 II

leetcode地址

20.二叉树：构造一棵最大的二叉树

讲义地址

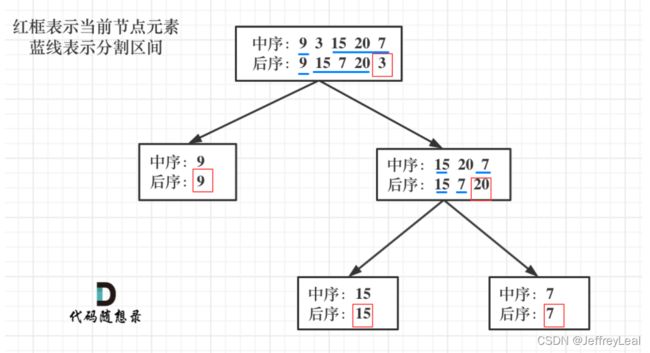
106.从中序与后序遍历序列构造二叉树

leetcode地址

新左数组：

新右数组：

class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        return Recurrent(inorder,0, inorder.length,
                postorder, 0, postorder.length);
    }
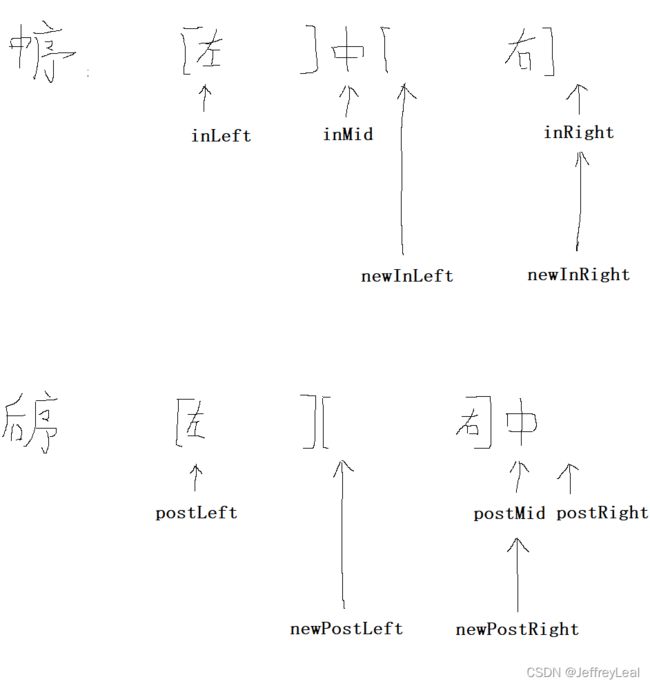
    // 变量都是左闭右开的，left指向数组起始位置，right指向末尾元素的下一个位置
    public TreeNode Recurrent(int[] inorder, int inLeft, int inRight,
                              int[] postorder, int postLeft, int postRight){
        if (inRight - inLeft == 0){
            return null;
        }
        // 1.找出中序数组中，中节点的位置
        int inMid = 0;
        int postMid = postRight -1;// 后序数组中，中节点的位置
        for (int i = inLeft; i < inRight; i++) {
            if (inorder[i] == postorder[postMid]){
                inMid = i;
                break;
            }
        }
        TreeNode node = new TreeNode(postorder[postMid]);

        // 2.划分后，左数组信息,
        // 如果先序数组只有一个元素，即inLeft + 1 = inRight,
        // 那么划分后，左数组的 newInLeft == newInRight，即左数组没有元素。
        // 这些变量只是方便阅读，实际中可以直接将新的值放到函数中
        int newInLeft = inLeft;
        int newInRight = inMid;
        int newPostLeft = postLeft;
        int newPostRight = postLeft + inMid - inLeft;
        node.left = Recurrent(inorder, newInLeft, newInRight,
                postorder, newPostLeft, newPostRight);

        // 3.划分后，右节点信息
        newInLeft = inMid + 1;
        newInRight = inRight;
        newPostLeft = postLeft + inMid - inLeft;
        newPostRight = postMid;
        node.right = Recurrent(inorder, newInLeft, newInRight,
                postorder, newPostLeft, newPostRight);
        return node;
    }
}

105.从前序与中序遍历序列构造二叉树

leetcode地址

21.本周小结！（二叉树系列三）

讲义地址

22.二叉树：合并两个二叉树

讲义地址

617.合并二叉树

leetcode地址

跟先序中序后续层次遍历无关。

方式一：递归

新建节点

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        return recurrent(root1, root2);
    }
    public TreeNode recurrent(TreeNode node1, TreeNode node2){
        if (node1 == null && node2 == null){
            return null;
        }
        TreeNode node = new TreeNode();
        if (node1 == null && node2 != null){
            node.val = node2.val;
            node.left = recurrent(null, node2.left);
            node.right = recurrent(null, node2.right);
        }
        if (node1 != null && node2 == null) {
            node.val = node1.val;
            node.left = recurrent(null, node1.left);
            node.right = recurrent(null, node1.right);
        }
        if (node1 != null && node2 != null) {
            node.val = node1.val + node2.val;
            node.left = recurrent(node1.left, node2.left);
            node.right = recurrent(node1.right, node2.right);
        }
        return node;
    }
}

合并才新建节点

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        return recurrent(root1, root2);
    }

    public TreeNode recurrent(TreeNode node1, TreeNode node2) {
        if (node1 == null) {
            return node2;
        }
        if (node2 == null) {
            return node1;
        }
        TreeNode node = new TreeNode(node1.val + node2.val);
        node.left = recurrent(node1.left, node2.left);
        node.right = recurrent(node1.right, node2.right);
        return node;
    }
}

方式二：非递归

合并才新建节点

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null){
            return root2;
        }
        if (root2 == null) {
            return root1;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode root = new TreeNode();
        stack.push(root2);
        stack.push(root1);
        stack.push(root);
        TreeNode node1;
        TreeNode node2;
        TreeNode cur;
        while (!stack.empty()) {
            cur = stack.pop();
            node1 = stack.pop();
            node2 = stack.pop();
            cur.val = node1.val + node2.val;

            // 处理当前节点的右节点
            if (node1.right == null) {
                cur.right = node2.right;
            } else if (node2.right == null) {
                cur.right = node1.right;
            }else {
                // node1.right != null && node1.right != null
                stack.push(node2.right);
                stack.push(node1.right);
                cur.right = new TreeNode();
                stack.push(cur.right);
            }
            // 处理当前节点的左节点
            if (node1.left == null) {
                cur.left = node2.left;
            } else if (node2.left == null) {
                cur.left = node1.left;
            }else {
                // node1.left != null && node1.left != null
                stack.push(node2.left);
                stack.push(node1.left);
                cur.left = new TreeNode();
                stack.push(cur.left);
            }
        }
        return root;
    }
}

23.二叉树：二叉搜索树登场！

讲义地址

700.二叉搜索树中的搜索

leetcode地址

和遍历无关。

方式一：递归

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        return preOrderRecurrent(root, val);
    }

    public TreeNode preOrderRecurrent(TreeNode node, int val) {
        if (node == null) {
            return null;
        }
        if (node.val == val) {
            return node;
        }
        TreeNode left = preOrderRecurrent(node.left, val);
        if (left != null) {
            return left;
        }
        TreeNode right = preOrderRecurrent(node.right, val);
        return right;
    }
}

方式二：非递归

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null){
            return null;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.add(root);
        while (!stack.empty()){
            TreeNode temp = stack.pop();
            if (temp.val == val){
                return temp;
            }
            if (temp.right != null){
                stack.push(temp.right);
            }
            if (temp.left != null){
                stack.push(temp.left);
            }
        }
        return null;
    }
}

24.二叉树：我是不是一棵二叉搜索树

讲义地址

98.验证二叉搜索树

leetcode地址

中序遍历的节点，如果是升序排列，那么这棵树就是二叉搜索树，这是中序的性质。要在遍历中进行比较，最主要是要记录上一个节点的值。

方式一：递归

class Solution {
    TreeNode min;

    public boolean isValidBST(TreeNode root) {
        return recurrent(root);
    }

    public boolean recurrent(TreeNode node) {
        if (node == null) {
            return true;
        }

        boolean leftRes = recurrent(node.left);
        // 如果左子树不满足，则提起终止
        if (!leftRes) {
            return false;
        }

        if (min != null && min.val >= node.val) {
            return false;
        }
        min = node;
        
        boolean rightRes = recurrent(node.right);
        
        return rightRes;
    }
}

方式二：非递归

class Solution {
    public boolean isValidBST(TreeNode root) {
        if (root == null) {
            return true;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        TreeNode min = null;
        while (cur != null || !stack.empty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            cur = stack.pop();
            if (min != null && min.val >= cur.val) {
                return false;
            }
            min = cur;
            cur = cur.right;
        }
        return true;
    }
}

25.二叉树：搜索树的最小绝对差

讲义地址

530.二叉搜索树的最小绝对差

leetcode地址

中序遍历。

方式一：递归

class Solution {
    TreeNode last;
    int res = Integer.MAX_VALUE;
    public int getMinimumDifference(TreeNode root) {
        inOrderRecurrent(root);
        return res;
    }
    public void inOrderRecurrent(TreeNode node){
        if (node == null){
            return;
        }
        inOrderRecurrent(node.left);

        if (last != null){
            res = Integer.min(res, Math.abs(last.val - node.val));
        }
        last = node;
        inOrderRecurrent(node.right);
    }
}

方式二：非递归

class Solution {
    public int getMinimumDifference(TreeNode root) {
        if (root == null || (root.left == null && root.right == null)) {
            return 0;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        TreeNode last = null; // 记录上一个节点
        int res = Integer.MAX_VALUE;
        while (cur != null || !stack.empty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            cur = stack.pop();
            if (last != null) {
                res = Integer.min(res, Math.abs(last. val - cur.val));
            }
            last = cur;
            cur = cur.right;
        }
        return res;
    }
}

26.二叉树：我的众数是多少？

讲义地址

501.二叉搜索树中的众数

leetcode地址

中序遍历。

方式一：递归

class Solution {
    ArrayList<Integer> resList = new ArrayList<>();
    int maxCount = 0;
    int count = 0;
    TreeNode pre = null;

    public int[] findMode(TreeNode root) {
        inOrderRecurrent(root);
        int len = resList.size();
        int[] res = new int[len];
        for (int i = 0; i < len; i++) {
            res[i] = resList.get(i);
        }
        return res;
    }

    public void inOrderRecurrent(TreeNode node) {
        if (node == null) {
            return;
        }

        inOrderRecurrent(node.left);

        int rootValue = node.val;
        // 计数
        if (pre == null || rootValue != pre.val) {
            count = 1;
        } else {
            count++;
        }
        // 更新结果以及maxCount
        if (count > maxCount) {
            resList.clear();
            resList.add(rootValue);
            maxCount = count;
        } else if (count == maxCount) {
            resList.add(rootValue);
        }

        pre = node;

        inOrderRecurrent(node.right);
    }
}

方式二：非递归

class Solution {
    public int[] findMode(TreeNode root) {
        ArrayList<Integer> resList = new ArrayList<>();
        int maxCount = 0;
        int count = 0;
        TreeNode pre = null;

        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()) {
            if (cur != null) {
                stack.push(cur);
                cur = cur.left;
            } else {
                cur = stack.pop();
                // 计数
                if (pre == null || cur.val != pre.val) {
                    count = 1;
                } else {
                    count++;
                }
                // 更新结果
                if (count > maxCount) {
                    maxCount = count;
                    resList.clear();
                    resList.add(cur.val);
                } else if (count == maxCount) {
                    resList.add(cur.val);
                }
                pre = cur;
                cur = cur.right;
            }
        }

        int len = resList.size();
        int[] res = new int[len];
        for (int i = 0; i < len; i++) {
            res[i] = resList.get(i);
        }
        return res;
//        return result.stream().mapToInt(Integer::intValue).toArray();
    }
}

27.二叉树：公共祖先问题

讲义地址

236. 二叉树的最近公共祖先

leetcode地址

前提条件：节点不重复。

此题属于回溯，非递归法不适合模拟回溯的过程。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        return postOrderRecurrent(root, p, q);
    }

    public TreeNode postOrderRecurrent(TreeNode node, TreeNode p, TreeNode q) {
        if (node == null || node == p || node == q) {// 递归结束条件
            return node;
        }

        TreeNode left = postOrderRecurrent(node.left, p, q);
        TreeNode right = postOrderRecurrent(node.right, p, q);

        if (left == null && right == null) {// 若未找到节点 p 或 q
            return null;
        }
        if (left != null && right == null) {// 若找到一个节点
            return left;
        }
        if (left == null && right != null) {// 若找到一个节点
            return right;
        }
        // 两个节点都找到
        return node;
    }
}

28.本周小结！（二叉树系列四）

讲义地址

29.二叉树：搜索树的公共祖先问题

讲义地址

235. 二叉搜索树的最近公共祖先

leetcode地址

前提条件：节点不重复，节点2个输入节点都是存在于树中。

与遍历顺序无关。

节点q，p的关系无非下面三种：相互不包含，q包含p，p包含q

那么公共节点s一定在区间【p，q】或者【q，p】里面。

当s为父节点的左节点时，那么它一定比右边的那些节点的值要小：

同理，当s为父节点的右节点时，那么它一定比左边的那些节点的值要小：

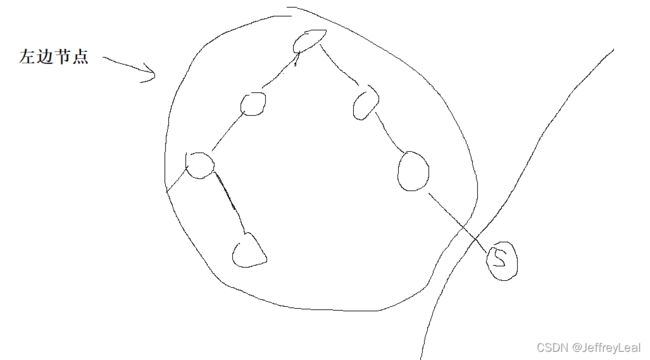
方式一：递归

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        return recurrent(root, p, q);
    }

    public TreeNode recurrent(TreeNode node, TreeNode p, TreeNode q) {
        if (node.val > p.val && node.val > q.val) {
            return recurrent(node.left, p, q);
        }
        if (node.val < p.val && node.val < q.val) {
            return recurrent(node.right, p, q);
        }
        return node;
    }
}

方式二：非递归

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        TreeNode temp = root;
        while (true) {
            if (temp.val > p.val && temp.val > q.val) {
                temp = temp.left;
            }else if (temp.val < p.val && temp.val < q.val) {
                temp = temp.right;
            }else {
                return temp;
            }
        }
    }
}

30.二叉树：搜索树中的插入操作

讲义地址

701.二叉搜索树中的插入操作

leetcode地址

方式一：递归

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        return recurrent(root,val);
    }
    public TreeNode recurrent(TreeNode node, int val){
        if (node == null){
            return new TreeNode(val);
        }
        if (node.val > val) {
            node.left = recurrent(node.left, val);
        }
        if (node.val < val) {
            node.right = recurrent(node.right,val);
        }
        return node;
    }
}

方式二：非递归

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            return root = new TreeNode(val);
        }
        TreeNode cur = root;
        while (true) {
            if (cur.val > val) {
                if (cur.left == null) {
                    cur.left = new TreeNode(val);
                    return root;
                }else {
                    cur = cur.left;
                }
            }else {
                if (cur.right == null) {
                    cur.right = new TreeNode(val);
                    return root;
                }else {
                    cur = cur.right;
                }
            }
        }
    }
}

31.二叉树：搜索树中的删除操作

讲义地址

450.删除二叉搜索树中的节点

leetcode地址

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        return delete(root, key);
    }

    private TreeNode delete(TreeNode node, int key) {
        if (node == null) {
            return null;
        }
        if (node.val > key) {
            node.left = delete(node.left, key);
        } else if (node.val < key) {
            node.right = delete(node.right, key);
        } else {
            // node.val == key，找到
            if (node.left == null) {
                return node.right;
            }
            if (node.right == null) {
                return node.left;
            }
            // 左右子节点都不为空
            TreeNode temp = node.right;
            // 找右子树的最小值
            while (temp.left != null) {
                temp = temp.left;
            }
            // 最小值移动到删除节点的位置
            node.val = temp.val;
            // 删除原来的最小值
            node.right = delete(node.right, temp.val);
        }
        return node;
    }
}

非递归法不适合。

32.二叉树：修剪一棵搜索树

讲义地址

669. 修剪二叉搜索树

leetcode地址

方式一：递归

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        return recurrent(root, low, high);
    }
    public TreeNode recurrent(TreeNode node, int low, int high){
        if (node == null) {
            return null;
        }
        if (node.val > high) {
            return recurrent(node.left, low, high);
        }
        if (node.val < low){
            return recurrent(node.right, low, high);
        }
        node.left = recurrent(node.left, low, high);
        node.right = recurrent(node.right, low, high);
        
        return node;
    }
}

小结

30，31，32这三章的思路非常相似。

33.二叉树：构造一棵搜索树

讲义地址

108.将有序数组转换为二叉搜索树

leetcode地址

方式一：递归

左闭右开 [left,right)，先序遍历。

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return recurrent(nums, 0, nums.length);
    }

    public TreeNode recurrent(int[] nums, int left, int right) {
        if (left >= right) {
            return null;
        }
        if (right - left == 1) {
            return new TreeNode(nums[left]);
        }
        int mid = left + ((right - left) >> 1);
        TreeNode node = new TreeNode(nums[mid]);

        node.left = recurrent(nums, left, mid);
        node.right = recurrent(nums, mid + 1, right);

        return node;
    }
}

方式二：非递归

左闭右开 [left,right)，层次遍历。

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        if (nums.length == 0) return null;

        //根节点初始化
        TreeNode root = new TreeNode();
        Queue<TreeNode> nodeQueue = new LinkedList<>();
        Queue<Integer> leftQueue = new LinkedList<>();
        Queue<Integer> rightQueue = new LinkedList<>();

        // 根节点入队列
        nodeQueue.offer(root);
        // 0为左区间下标初始位置
        leftQueue.offer(0);
        // nums.size()为右区间下标初始位置
        rightQueue.offer(nums.length);

        while (!nodeQueue.isEmpty()) {
            TreeNode cur = nodeQueue.poll();
            int left = leftQueue.poll();
            int right = rightQueue.poll();
            int mid = left + ((right - left) >> 1);

            // 将mid对应的元素给中间节点
            cur.val = nums[mid];

            // 处理左区间
            if (left < mid) {
                cur.left = new TreeNode();
                nodeQueue.offer(cur.left);
                leftQueue.offer(left);
                rightQueue.offer(mid);
            }

            // 处理右区间
            if (right > mid + 1) {
                cur.right = new TreeNode();
                nodeQueue.offer(cur.right);
                leftQueue.offer(mid + 1);
                rightQueue.offer(right);
            }
        }
        return root;
    }
}

用多了2个队列去模拟递归中的输入参数。

34.二叉树：搜索树转成累加树

讲义地址

538.把二叉搜索树转换为累加树

leetcode地址

右中左的中序遍历。

方式一：递归

class Solution {
    int sum = 0;

    public TreeNode convertBST(TreeNode root) {
        recurrent(root);
        return root;
    }

    public void recurrent(TreeNode node) {
        if (node == null) {
            return;
        }
        recurrent(node.right);
        sum += node.val;
        node.val = sum;
        recurrent(node.left);
    }
}

方式二：非递归

class Solution {
    public TreeNode convertBST(TreeNode root) {
        int sum = 0;
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.empty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.right;
            }
            cur = stack.pop();
            sum += cur.val;
            cur.val = sum;
            cur = cur.left;
        }
        return root;
    }
}

35.二叉树：总结篇！（需要掌握的二叉树技能都在这里了）

讲义地址

总结

if (与遍历有关) {
    先序中序后序层次遍历；
    各种遍历的性质：
    比如：中序遍历的序列如果是降序排列的，那么它就是搜索二叉树
    if (递归) {
         1. 选择输入参数
         2. 终止条件
         3. 本轮递归的操作
         4. 返回值
    }else {
         非递归
    }
}else {
    与遍历无关
}

if (自顶向下) {
    比如计算深度、层数，单路径往下的
}else {
    自底向上
    比如向上递归返回子树的高度
}

各种结构的判断条件：
比如：叶节点的条件：一个节点的子节点存在，且子节点的左右子节点都为空；

你可能感兴趣的:(算法与数据结构,leetcode,算法,深度优先)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
回溯 Leetcode 332 重新安排行程 mmaerd Leetcode刷题学习记录 leetcode 算法职场和发展
重新安排行程Leetcode332学习记录自代码随想录给你一份航线列表tickets，其中tickets[i]=[fromi,toi]表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从JFK（肯尼迪国际机场）出发的先生，所以该行程必须从JFK开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。例如，行程[“JFK”,“LGA”]与[“JFK”,“LGB
Goolge earth studio 进阶4——路径修改与平滑陟彼高冈yu Google earth studio 进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
基于社交网络算法优化的二维最大熵图像分割智能算法研学社（Jack旭）智能优化算法应用图像分割算法 php 开发语言
智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
509. 斐波那契数(每日一题) lzyprime
lzyprime博客(github)创建时间：2021.01.04qq及邮箱：2383518170leetcode笔记题目描述斐波那契数，通常用F(n)表示，形成的序列称为斐波那契数列。该数列由0和1开始，后面的每一项数字都是前面两项数字的和。也就是：F(0)=0，F(1)=1F(n)=F(n-1)+F(n-2)，其中n>1给你n，请计算F(n)。示例1：输入：2输出：1解释：F(2)=F(1)+
121. 买卖股票的最佳时机薄荷糖的味道_fb40
给定一个数组，它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天（股票价格=1）的时候买入，在第5天（股票价格=6）的时候卖出，最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
回溯算法-重新安排行程 chirou_ 算法数据结构图论 c++图搜索
leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
C++ | Leetcode C++题解之第409题最长回文串 Ddddddd_158 经验分享 C++Leetcode 题解
题目：题解：classSolution{public:intlongestPalindrome(strings){unordered_mapcount;intans=0;for(charc:s)++count[c];for(autop:count){intv=p.second;ans+=v/2*2;if(v%2==1andans%2==0)++ans;}returnans;}};
Faiss：高效相似性搜索与聚类的利器网络·魚大数据 faiss
Faiss是一个针对大规模向量集合的相似性搜索库，由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构，用于加速向量之间的相似性搜索，特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理：近似最近邻搜索：Faiss的核心功能之一是近似最近邻搜索，它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的，
insert into select 主键自增_mybatis拦截器实现主键自动生成 weixin_39521651 insert into select 主键自增 mybatis delete返回值 mybatis insert返回主键 mybatis insert返回对象 mybatis plus insert返回主键 mybatis plus 插入生成id
前言前阵子和朋友聊天，他说他们项目有个需求，要实现主键自动生成，不想每次新增的时候，都手动设置主键。于是我就问他，那你们数据库表设置主键自动递增不就得了。他的回答是他们项目目前的id都是采用雪花算法来生成，因此为了项目稳定性，不会切换id的生成方式。朋友问我有没有什么实现思路，他们公司的orm框架是mybatis，我就建议他说，不然让你老大把mybatis切换成mybatis-plus。mybat
k均值聚类算法考试例题_k均值算法(k均值聚类算法计算题) 寻找你83497 k均值聚类算法考试例题
?算法：第一步：选K个初始聚类中心，z1(1),z2(1)，…，zK(1)，其中括号内的序号为寻找聚类中心的迭代运算的次序号。聚类中心的向量值可任意设定，例如可选开始的K个.k均值聚类：---------一种硬聚类算法，隶属度只有两个取值0或1，提出的基本根据是“类内误差平方和最小化”准则；模糊的c均值聚类算法：--------一种模糊聚类算法，是.K均值聚类算法是先随机选取K个对象作为初始的聚类
Python实现简单的机器学习算法 master_chenchengg python python 办公效率 python开发 IT
Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
推荐算法_隐语义-梯度下降 _feivirus_ 算法机器学习和数学推荐算法机器学习隐语义
importnumpyasnp1.模型实现"""inputrate_matrix:M行N列的评分矩阵，值为P*Q.P:初始化用户特征矩阵M*K.Q:初始化物品特征矩阵K*N.latent_feature_cnt:隐特征的向量个数max_iteration:最大迭代次数alpha:步长lamda:正则化系数output分解之后的P和Q"""defLFM_grad_desc(rate_matrix,l
K近邻算法_分类鸢尾花数据集 _feivirus_ 算法机器学习和数学分类机器学习 K近邻
importnumpyasnpimportpandasaspdfromsklearn.datasetsimportload_irisfromsklearn.model_selectionimporttrain_test_splitfromsklearn.metricsimportaccuracy_score1.数据预处理iris=load_iris()df=pd.DataFrame(data=ir
数据结构 | 栈和队列 TT-Kun 数据结构与算法数据结构栈队列 C语言
文章目录栈和队列1.栈：后进先出（LIFO）的数据结构1.1概念与结构1.2栈的实现2.队列：先进先出（FIFO）的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中，栈和队列是两种基本且重要的数据结构，它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
[Python] 数据结构详解及代码 AIAdvocate 算法 python 数据结构链表
今日内容大纲介绍数据结构介绍列表链表1.数据结构和算法简介程序大白话翻译,程序=数据结构+算法数据结构指的是存储,组织数据的方式.算法指的是为了解决实际业务问题而思考思路和方法,就叫:算法.2.算法的5大特性介绍算法具有独立性算法是解决问题的思路和方式,最重要的是思维,而不是语言,其(算法)可以通过多种语言进行演绎.5大特性有输入,需要传入1或者多个参数有输出,需要返回1个或者多个结果有穷性,执行
Python算法L5：贪心算法小熊同学哦 Python算法算法 python 贪心算法
Python贪心算法简介目录Python贪心算法简介贪心算法的基本步骤贪心算法的适用场景经典贪心算法问题1.**零钱兑换问题**2.**区间调度问题**3.**背包问题**贪心算法的优缺点优点：缺点：结语贪心算法（GreedyAlgorithm）是一种在每一步选择中都采取当前最优或最优解的算法。它的核心思想是，在保证每一步局部最优的情况下，希望通过贪心选择达到全局最优解。虽然贪心算法并不总能得到全
【RabbitMQ 项目】服务端：数据管理模块之绑定管理月夜星辉雪 rabbitmq 分布式
文章目录一.编写思路二.代码实践一.编写思路定义绑定信息类交换机名称队列名称绑定关键字：交换机的路由交换算法中会用到没有是否持久化的标志，因为绑定是否持久化取决于交换机和队列是否持久化，只有它们都持久化时绑定才需要持久化。绑定就好像一根绳子，两端连接着交换机和队列，当一方不存在，它就没有存在的必要了定义绑定持久化类构造函数：如果数据库文件不存在则创建，打开数据库，创建binding_table插入
非对称加密算法原理与应用2——RSA私钥加密文件私语茶馆云部署与开发架构及产品灵感记录 RSA2048 私钥加密
作者：私语茶馆1.相关章节（1）非对称加密算法原理与应用1——秘钥的生成-CSDN博客第一章节讲述的是创建秘钥对，并将公钥和私钥导出为文件格式存储。本章节继续讲如何利用私钥加密内容，包括从密钥库或文件中读取私钥，并用RSA算法加密文件和String。2.私钥加密的概述本文主要基于第一章节的RSA2048bit的非对称加密算法讲述如何利用私钥加密文件。这种加密后的文件，只能由该私钥对应的公钥来解密。
粒子群优化 (PSO) 在三维正弦波函数中的应用 subject625Ruben 机器学习人工智能 matlab 算法
在这篇博客中，我们将展示如何使用粒子群优化（PSO）算法求解三维正弦波函数，并通过增加正弦波扰动，使优化过程更加复杂和有趣。本文将介绍目标函数的定义、PSO参数设置以及算法执行的详细过程，并展示搜索空间中的动态过程和收敛曲线。1.目标函数定义我们使用的目标函数是一个三维正弦波函数，定义如下：objectiveFunc=@(x)sin(sqrt(x(1).^2+x(2).^2))+0.5*sin(5
leetcode-617. 合并二叉树 manba_ leetcode hot100 leetcode 算法
题目描述给你两棵二叉树：root1和root2。想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为null的节点将直接作为新二叉树的节点。返回合并后的二叉树。注意:合并过程必须从两个树的根节点开始。示例1：输入：root1=[1,3,2,
非对称加密算法————RSA理论及详情 hu19930613
转自：https://www.kancloud.cn/kancloud/rsa_algorithm/48484一、一点历史1976年以前，所有的加密方法都是同一种模式：（1）甲方选择某一种加密规则，对信息进行加密；（2）乙方使用同一种规则，对信息进行解密。由于加密和解密使用同样规则（简称"密钥"），这被称为"对称加密算法"（Symmetric-keyalgorithm）。这种加密模式有一个最大弱点
ai绘画工具midjourney怎么下载？附作品管理教程设计师早上好
Midjourney是一款功能强大的AI绘画工具，它使用机器学习技术和深度神经网络等算法，可以生成各种艺术风格的绘画作品。在创意设计、广告宣传等方面有着广泛的应用前景。那么，ai绘画工具midjourney怎么下载？本文将为您介绍Midjourney的下载以及作品的相关管理。一、Midjourney下载Midjourney的下载非常简单，只需打开Midjourney官网（点击“GetMidjour
【加密算法基础——对称加密和非对称加密】 XWWW668899 网络安全服务器笔记
对称加密与非对称加密对称加密和非对称加密是两种基本的加密方法，各自有不同的特点和用途。以下是详细比较：1.对称加密特点密钥:使用相同的密钥进行加密和解密。发送方和接收方必须共享这个密钥。速度:通常速度较快，适合处理大量数据。实现:算法相对简单，计算效率高。常见算法AES(高级加密标准)DES(数据加密标准)3DES(三重数据加密标准)RC4(流密码)应用场景文件加密磁盘加密传输大量数据时的加密2.
代码随想录Day 41|动态规划之买卖股票问题，leetcode题目121. 买卖股票的最佳时机、122. 买卖股票的最佳时机Ⅱ、123. 买卖股票的最佳时机Ⅲ LluckyYH 动态规划 leetcode 算法数据结构
提示：DDU，供自己复习使用。欢迎大家前来讨论~文章目录买卖股票的最佳时机相关题目题目一：121.买卖股票的最佳时机解题思路：题目二：122.买卖股票的最佳时机II解题思路：题目三：123.买卖股票的最佳时机III解题思路总结买卖股票的最佳时机相关题目题目一：121.买卖股票的最佳时机[[121.买卖股票的最佳时机](https://leetcode.cn/problems/combination
【算法练习】IDEA集成leetcode插件实现快速刷 2401_84102892 2024年程序员学习算法 intellij-idea leetcode
============点击右侧边leetcode->设置->配置地址、用户名、密码、存放目录、文件模板用户名要登录后在账号信息里看模板代码1.codefilename!velocityTool.camelC
Day_11 ROC_bird.. 算法
面试题16.15.珠玑妙算-力扣（LeetCode）/***Note:Thereturnedarraymustbemalloced,assumecallercallsfree().*///下标和对应位置的值都一样，answer[0]+1,对应位置的值猜对了，但是下标不对，answer[1]+1int*masterMind(char*solution,char*guess,int*returnSiz
【加密算法基础——RSA 加密】 XWWW668899 网络服务器笔记 python
RSA加密RSA（Rivest-Shamir-Adleman）加密是非对称加密，一种广泛使用的公钥加密算法，主要用于安全数据传输。公钥用于加密，私钥用于解密。RSA加密算法的名称来源于其三位发明者的姓氏：R:RonRivestS:AdiShamirA:LeonardAdleman这三位计算机科学家在1977年共同提出了这一算法，并发表了相关论文。他们的工作为公钥加密的基础奠定了重要基础，使得安全通
LeetCode 53. Maximum Subarray 枯萎的海风算法与OJ C/C++leetcode
1.题目描述Findthecontiguoussubarraywithinanarray(containingatleastonenumber)whichhasthelargestsum.Forexample,giventhearray[−2,1,−3,4,−1,2,1,−5,4],thecontiguoussubarray[4,−1,2,1]hasthelargestsum=6.clicktos
Linux的Initrd机制被触发 linux
Linux 的 initrd 技术是一个非常普遍使用的机制，linux2.6 内核的 initrd 的文件格式由原来的文件系统镜像文件转变成了 cpio 格式，变化不仅反映在文件格式上， linux 内核对这两种格式的 initrd 的处理有着截然的不同。本文首先介绍了什么是 initrd 技术，然后分别介绍了 Linux2.4 内核和 2.6 内核的 initrd 的处理流程。最后通过对 Lin
maven本地仓库路径修改 bitcarter maven
默认maven本地仓库路径：C:\Users\Administrator\.m2 修改maven本地仓库路径方法： 1.打开E:\maven\apache-maven-2.2.1\conf\settings.xml 2.找到
XSD和XML中的命名空间 darrenzhu xml xsd schema namespace 命名空间
http://www.360doc.com/content/12/0418/10/9437165_204585479.shtml http://blog.csdn.net/wanghuan203/article/details/9203621 http://blog.csdn.net/wanghuan203/article/details/9204337 http://www.cn
Java 求素数运算周凡杨 java 算法素数
网络上对求素数之解数不胜数，我在此总结归纳一下，同时对一些编码，加以改进，效率有成倍热提高。第一种：原理: 6N(+-)1法任何一个自然数，总可以表示成为如下的形式之一： 6N，6N+1，6N+2，6N+3，6N+4，6N+5 (N=0，1，2，…)
java 单例模式 g21121 java
想必单例模式大家都不会陌生，有如下两种方式来实现单例模式： class Singleton { private static Singleton instance=new Singleton(); private Singleton(){} static Singleton getInstance() { return instance; }
Linux下Mysql源码安装 510888780 mysql
1.假设已经有mysql-5.6.23-linux-glibc2.5-x86_64.tar.gz (1)创建mysql的安装目录及数据库存放目录解压缩下载的源码包，目录结构，特殊指定的目录除外：
32位和64位操作系统墙头上一根草 32位和64位操作系统
32位和64位操作系统是指：CPU一次处理数据的能力是32位还是64位。现在市场上的CPU一般都是64位的，但是这些CPU并不是真正意义上的64 位CPU，里面依然保留了大部分32位的技术，只是进行了部分64位的改进。32位和64位的区别还涉及了内存的寻址方面，32位系统的最大寻址空间是2 的32次方= 4294967296（bit）= 4（GB）左右，而64位系统的最大寻址空间的寻址空间则达到了
我的spring学习笔记10-轻量级_Spring框架 aijuans Spring 3
一、问题提问： → 请简单介绍一下什么是轻量级？轻量级（Leightweight）是相对于一些重量级的容器来说的，比如Spring的核心是一个轻量级的容器，Spring的核心包在文件容量上只有不到1M大小，使用Spring核心包所需要的资源也是很少的，您甚至可以在小型设备中使用Spring。
mongodb 环境搭建及简单CURD antlove Web Install curd NoSQL mongo
一搭建mongodb环境 1. 在mongo官网下载mongodb 2. 在本地创建目录 "D:\Program Files\mongodb-win32-i386-2.6.4\data\db" 3. 运行mongodb服务 [mongod.exe --dbpath "D:\Program Files\mongodb-win32-i386-2.6.4\data\
数据字典和动态视图百合不是茶 oracle 数据字典动态视图系统和对象权限
数据字典（data dictionary）是 Oracle 数据库的一个重要组成部分，这是一组用于记录数据库信息的只读（read-only）表。随着数据库的启动而启动,数据库关闭时数据字典也关闭数据字典中包含数据库中所有方案对象（schema object）的定义(包括表，视图，索引，簇，同义词，序列，过程，函数，包，触发器等等) 数据库为一
多线程编程一般规则 bijian1013 java thread 多线程 java多线程
如果两个工两个以上的线程都修改一个对象，那么把执行修改的方法定义为被同步的，如果对象更新影响到只读方法，那么只读方法也要定义成同步的。不要滥用同步。如果在一个对象内的不同的方法访问的不是同一个数据，就不要将方法设置为synchronized的。
将文件或目录拷贝到另一个Linux系统的命令scp bijian1013 linux unix scp
一.功能说明 scp就是security copy，用于将文件或者目录从一个Linux系统拷贝到另一个Linux系统下。scp传输数据用的是SSH协议，保证了数据传输的安全，其格式如下： scp 远程用户名@IP地址：文件的绝对路径
【持久化框架MyBatis3五】MyBatis3一对多关联查询 bit1129 Mybatis3
以教员和课程为例介绍一对多关联关系，在这里认为一个教员可以叫多门课程，而一门课程只有1个教员教，这种关系在实际中不太常见，通过教员和课程是多对多的关系。示例数据：地址表： CREATE TABLE ADDRESSES ( ADDR_ID INT(11) NOT NULL AUTO_INCREMENT, STREET VAR
cookie状态判断引发的查找问题 bitcarter form cgi
先说一下我们的业务背景： 1.前台将图片和文本通过form表单提交到后台，图片我们都做了base64的编码，并且前台图片进行了压缩 2.form中action是一个cgi服务 3.后台cgi服务同时供PC，H5，APP 4.后台cgi中调用公共的cookie状态判断方法（公共的，大家都用，几年了没有问题）问题：（折腾两天。。。。） 1.PC端cgi服务正常调用，cookie判断没
通过Nginx,Tomcat访问日志(access log)记录请求耗时 ronin47
一、Nginx通过$upstream_response_time $request_time统计请求和后台服务响应时间 nginx.conf使用配置方式： log_format main '$remote_addr - $remote_user [$time_local] "$request" ''$status $body_bytes_sent "$http_r
java-67- n个骰子的点数。把n个骰子扔在地上，所有骰子朝上一面的点数之和为S。输入n，打印出S的所有可能的值出现的概率。 bylijinnan java
public class ProbabilityOfDice { /** * Q67 n个骰子的点数 * 把n个骰子扔在地上，所有骰子朝上一面的点数之和为S。输入n，打印出S的所有可能的值出现的概率。 * 在以下求解过程中，我们把骰子看作是有序的。 * 例如当n=2时，我们认为（1，2）和（2，1）是两种不同的情况 */ private stati
看别人的博客，觉得心情很好 Cb123456 博客心情
以为写博客，就是总结，就和日记一样吧，同时也在督促自己。今天看了好长时间博客: 职业规划: http://www.iteye.com/blogs/subjects/zhiyeguihua android学习: 1.http://byandby.i
[JWFD开源工作流]尝试用原生代码引擎实现循环反馈拓扑分析 comsci 工作流
我们已经不满足于仅仅跳跃一次，通过对引擎的升级，今天我测试了一下循环反馈模式，大概跑了200圈，引擎报一个溢出错误在一个流程图的结束节点中嵌入一段方程，每次引擎运行到这个节点的时候，通过实时编译器GM模块，计算这个方程，计算结果与预设值进行比较，符合条件则跳跃到开始节点，继续新一轮拓扑分析，直到遇到
JS常用的事件及方法 cwqcwqmax9 js
事件描述 onactivate 当对象设置为活动元素时触发。 onafterupdate 当成功更新数据源对象中的关联对象后在数据绑定对象上触发。 onbeforeactivate 对象要被设置为当前元素前立即触发。 onbeforecut 当选中区从文档中删除之前在源对象触发。 onbeforedeactivate 在 activeElement 从当前对象变为父文档其它对象之前立即
正则表达式验证日期格式 dashuaifu 正则表达式 IT其它 java其它
正则表达式验证日期格式 function isDate(d){ var v = d.match(/^(\d{4})-(\d{1,2})-(\d{1,2})$/i); if(!v) { this.focus(); return false; } } <input value="2000-8-8" onblu
Yii CModel.rules() 方法、validate预定义完整列表、以及说说验证 dcj3sjt126com yii
public array rules () {return} array 要调用 validate() 时应用的有效性规则。返回属性的有效性规则。声明验证规则，应重写此方法。每个规则是数组具有以下结构：array('attribute list', 'validator name', 'on'=>'scenario name', ...validation
UITextAttributeTextColor = deprecated in iOS 7.0 dcj3sjt126com ios
In this lesson we used the key "UITextAttributeTextColor" to change the color of the UINavigationBar appearance to white. This prompts a warning "first deprecated in iOS 7.0." Ins
判断一个数是质数的几种方法 EmmaZhao Math python
质数也叫素数，是只能被1和它本身整除的正整数，最小的质数是2，目前发现的最大的质数是p=2^57885161-1【注1】。判断一个数是质数的最简单的方法如下： def isPrime1(n): for i in range(2, n): if n % i == 0: return False return True 但是在上面的方法中有一些冗余的计算，所以
SpringSecurity工作原理小解读坏我一锅粥 SpringSecurity
SecurityContextPersistenceFilter ConcurrentSessionFilter WebAsyncManagerIntegrationFilter HeaderWriterFilter CsrfFilter LogoutFilter Use
JS实现自适应宽度的Tag切换 ini JavaScript html Web css html5
效果体验：http://hovertree.com/texiao/js/3.htm 该效果使用纯JavaScript代码，实现TAB页切换效果，TAB标签根据内容自适应宽度，点击TAB标签切换内容页。 HTML文件代码： <!DOCTYPE html> <html xmlns="http://www.w3.org/1999/xhtml"
Hbase Rest API : 数据查询 kane_xie REST hbase
hbase（hadoop）是用java编写的，有些语言（例如python）能够对它提供良好的支持，但也有很多语言使用起来并不是那么方便，比如c#只能通过thrift访问。Rest就能很好的解决这个问题。Hbase的org.apache.hadoop.hbase.rest包提供了rest接口，它内嵌了jetty作为servlet容器。启动命令：./bin/hbase rest s
JQuery实现鼠标拖动元素移动位置（源码+注释）明子健 jquery js 源码拖动鼠标
欢迎讨论指正！ print.html代码： <!DOCTYPE html> <html> <head> <meta http-equiv=Content-Type content="text/html;charset=utf-8"> <title>发票打印</title> &l
Postgresql 连表更新字段语法 update qifeifei PostgreSQL
下面这段sql本来目的是想更新条件下的数据，可是这段sql却更新了整个表的数据。sql如下： UPDATE tops_visa.visa_order SET op_audit_abort_pass_date = now() FROM tops_visa.visa_order as t1 INNER JOIN tops_visa.visa_visitor as t2 ON t1.
将redis,memcache结合使用的方案? tcrct redis cache
公司架构上使用了阿里云的服务，由于阿里的kvstore收费相当高，打算自建，自建后就需要自己维护，所以就有了一个想法，针对kvstore(redis)及ocs(memcache)的特点，想自己开发一个cache层，将需要用到list，set，map等redis方法的继续使用redis来完成，将整条记录放在memcache下，即findbyid，save等时就memcache，其它就对应使用redi
开发中遇到的诡异的bug wudixiaotie bug
今天我们服务器组遇到个问题：我们的服务是从Kafka里面取出数据，然后把offset存储到ssdb中，每个topic和partition都对应ssdb中不同的key，服务启动之后，每次kafka数据更新我们这边收到消息，然后存储之后就发现ssdb的值偶尔是-2,这就奇怪了，最开始我们是在代码中打印存储的日志，发现没什么问题，后来去查看ssdb的日志，才发现里面每次set的时候都会对同一个key

电信保温杯笔记——代码随想录 刷题攻略 二叉树