K-Means聚类算法

引言

聚类算法是传统机器学习算法中比较重要的一个算法，也是工程项目当中一个比较常用的算法。

一. 分类与聚类

分类
分类其实是从特定的数据中挖掘模式，作出判断的过程。
分类学习主要过程：
（1）训练数据集存在一个类标记号，判断它是正向数据集（起积极作用，不垃圾邮件）， 还是负向数据集（起抑制作用，垃圾邮件）；
（2）然后需要对数据集进行学习训练，并构建一个训练的模型；
（3）通过该模型对预测数据集进预测，并计算其结果的性能。

这里举例说明分类的过程，在日常生活中，我们都使用过电子邮箱，在电子邮箱里，有一个垃圾邮箱的分类器，为什么有时候来了邮件它自动地就给你分到垃圾邮件里去了。这是一个自动的过程。但实际上，在你刚开始使用邮箱时，它是不能够对垃圾邮件进行分类的，在使用过程中，我们会首先人工地标注哪些是垃圾邮件，长此以往，邮箱就能进行垃圾邮件的过滤了。总之，之所以能进行垃圾邮件的分类，都是因为有历史数据来支撑。在这里有两个重要的概念，一个是历史数据，一个是类别标签。

聚类
从广义上说，聚类就是将数据集中在某些方面相似的数据成员放在一起。
一个聚类就是一些数据实例的集合，其中处于相同聚类中的数据元素彼此相似，但是处于不 同聚类中的元素彼此不同。
由于在聚类中那些表示数据类别的分类或分组信息是没有的，即这些数据是没有标签的，所 以聚类通常被归为无监督学习（Unsupervised Learning）。

同样以邮箱为例，聚类同样可以把邮件分为两大类，但是区别在于邮箱系统并不知道这两大类的含义，也就是说这两大类是没有标签的。

如图是一个800篇文章数据集的聚类结果，我们可以看到这里聚成了4堆，聚类的结果是没有图例（标签）的，图例是手动添加的。所以在聚类完成后，大家是不知道这4堆数据的含义的。聚类算法的本质是去找相似点，算法认为这两个元素相似的话，就会聚成一堆。
聚类的目的也是把数据分类，但是事先是不知道如何去分的，完全是算法自己来判断各条数 据之间的相似性，相似的就放在一起。
在聚类的结论出来之前，完全不知道每一类有什么特点，一定要根据聚类的结果通过人的经 验来分析，看看聚成的这一类大概有什么特点。
总之，聚类主要是"物以类聚"，通过相似性把相似元素聚集在一起，它没有标签；而分类通 过标签来训练得到一个模型，对新数据集进行预测的过程，其数据存在标签。

聚类样本间的属性

1. 有序属性：西瓜的甜度：0.1,0.5,0.9
2. 无序属性：性别：男，女

聚类中更多的是处理有序属性

聚类的常见算法
聚类算法分为三大类：

1. 原型聚类：

• K均值聚类算法

2. 层次聚类
3. 密度聚类

二. K - Means聚类

K-Means聚类
K-Means聚类是最常用的聚类算法，最初起源于信号处理，其目标是将数据点划分为K个类簇。 该算法的最大优点是简单、便于理解，运算速度较快，缺点是要在聚类前指定聚集的类簇数。 k-means算法是一种原型聚类算法。

k-means聚类算法的分析流程：
第一步，确定K值，即将数据集聚集成K个类簇或小组。
第二步，从数据集中随机选择K个数据点作为质心（Centroid）或数据中心。
第三步，分别计算每个点到每个质心之间的距离，并将每个点划分到离最近质心的小组。
第四步，当每个质心都聚集了一些点后，重新定义算法选出新的质心。（对于每个簇，计 算其均值，即得到新的k个质心点）
第五步，迭代执行第三步到第四步，直到迭代终止条件满足为止（聚类结果不再变化）

注意：k-means聚类算法只提供了思想，里面实现的具体细节可以灵活改变，比如计算距离时我们可以用欧氏距离，但我们也可以用其他的距离度量方式，定义质心时我们可以计算均值，也可以计算中值等。

下面举例说明：

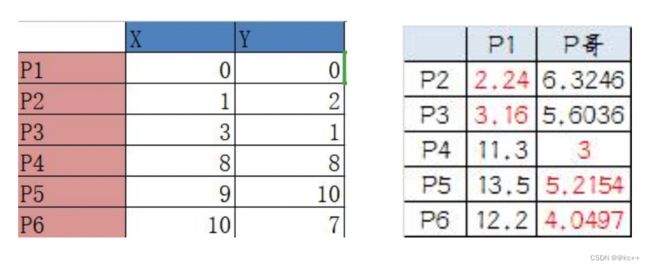
这里手写了6个点，在这里我们通过人眼观察就能知道 k 值取2比较合适，现在验证，当k取2时，P1到P3应该为一堆，P4到P6应该为一堆

第一步，确定K值，即将数据集聚集成K个类簇或小组。
----这里我们选K=2
第二步，从数据集中随机选择K个数据点作为质心（Centroid）或数 据中心。
----假设我们选择P1和P2作为初始的质心
第三步，分别计算每个点到每个质心之间的距离，并将每个点划分 到离最近质心的小组。
----计算P3到P1的距离：√10 = 3.16；
----计算P3到P2的距离：√((3-1)^2+(1-2)2 = √5 = 2.24；
----所以P3离P2更近，P3就加入P2的簇。同理，P4、P5、P6；

P3到P6都跟P2更近，所以第一次分组的结果是：

• 组A：P1
• 组B：P2、P3、P4、P5、P6

第四步，当每个质心都聚集了一些点后，重新定义算法选出新的质心。
（对于每个簇，计算其均值，即得到新的k个质心点）
----组A没啥可选的，还是P1自己
----组B有五个点，需要选新质心。这里要注意选择的方法是每个组X坐标的平均值和Y坐标的平均值组成的新的点，为新质心，也就是说这个质心是“虚拟的”。
----因此，B组选出新质心的坐标为：P哥（（1+3+8+9+10）/5， （2+1+8+10+7）/5）=（6.2，5.6）。
----综合两组，新质心为P1（0，0），P哥（6.2，5.6）。
----而P2-P6重新成为离散点。

再次计算点到质心的距离：
这时可以看到P2、P3离P1更近，P4、P5、P6离P哥更近。
第二次分组的结果是：

• 组A：P1、P2、P3
• 组B：P4、P5、P6（虚拟质心这时候消失）
  

按照上一次的方法选出两个新的虚拟质心：
----P哥1（1.33，1）， P哥2（9，8.33）。
第三次计算点到质心的距离：
---- 这时可以看到P1、P2、P3离P哥1更近，P4、 P5、P6离P哥2更近。
---- 所以第三次分组的结果是：

• 组A：P1、P2、P3
• 组B：P4、P5、P6

我们发现，这次分组的结果和上次没有任何变化了，说 明已经收敛，聚类结束。

代码实现

调用Kmeans函数

# coding: utf-8

'''
在OpenCV中，Kmeans()函数原型如下所示：
retval, bestLabels, centers = kmeans(data, K, bestLabels, criteria, attempts, flags[, centers])
    data表示聚类数据，最好是np.flloat32类型的N维点集
    K表示聚类类簇数
    bestLabels表示输出的整数数组，用于存储每个样本的聚类标签索引
    criteria表示迭代停止的模式选择，这是一个含有三个元素的元组型数。格式为（type, max_iter, epsilon）
        其中，type有如下模式：
         —–cv2.TERM_CRITERIA_EPS :精确度（误差）满足epsilon停止。
         —-cv2.TERM_CRITERIA_MAX_ITER：迭代次数超过max_iter停止。
         —-cv2.TERM_CRITERIA_EPS+cv2.TERM_CRITERIA_MAX_ITER，两者合体，任意一个满足结束。
    attempts表示重复试验kmeans算法的次数，算法返回产生的最佳结果的标签
    flags表示初始中心的选择，两种方法是cv2.KMEANS_PP_CENTERS ;和cv2.KMEANS_RANDOM_CENTERS
    centers表示集群中心的输出矩阵，每个集群中心为一行数据
'''

import cv2
import numpy as np
import matplotlib.pyplot as plt

#读取原始图像灰度颜色
img = cv2.imread('lenna.png', 0) 
print (img.shape)

#获取图像高度、宽度
rows, cols = img.shape[:]

#图像二维像素转换为一维
data = img.reshape((rows * cols, 1))
data = np.float32(data)

#停止条件 (type,max_iter,epsilon)
criteria = (cv2.TERM_CRITERIA_EPS +
            cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)

#设置标签
flags = cv2.KMEANS_RANDOM_CENTERS

#K-Means聚类 聚集成4类
compactness, labels, centers = cv2.kmeans(data, 4, None, criteria, 10, flags)

#生成最终图像
dst = labels.reshape((img.shape[0], img.shape[1]))

#用来正常显示中文标签
plt.rcParams['font.sans-serif']=['SimHei']

#显示图像
titles = [u'原始图像', u'聚类图像']  
images = [img, dst]  
for i in range(2):  
   plt.subplot(1,2,i+1), plt.imshow(images[i], 'gray'), 
   plt.title(titles[i])  
   plt.xticks([]),plt.yticks([])  
plt.show()

K-Means聚类与图像处理
在图像处理中，通过K-Means聚类算法可以实现图像分割、图像聚类、图像识别等操作。 我们通过K-Means可以将这些像素点聚类成K个簇，然后使用每个簇内的质心点来替换簇内所有的像素点，这样就能实现在不改变分辨率的情况下量化压缩图像颜色，实现图像颜色层级分割。

聚类的算法实际上并不关心你的数据集是什么，下面以篮球运动员比赛数据为例继续进行聚类

# coding=utf-8  
from sklearn.cluster import KMeans
 
"""
第一部分：数据集
X表示二维矩阵数据，篮球运动员比赛数据
总共20行，每行两列数据
第一列表示球员每分钟助攻数：assists_per_minute
第二列表示球员每分钟得分数：points_per_minute
"""
X = [[0.0888, 0.5885],
     [0.1399, 0.8291],
     [0.0747, 0.4974],
     [0.0983, 0.5772],
     [0.1276, 0.5703],
     [0.1671, 0.5835],
     [0.1306, 0.5276],
     [0.1061, 0.5523],
     [0.2446, 0.4007],
     [0.1670, 0.4770],
     [0.2485, 0.4313],
     [0.1227, 0.4909],
     [0.1240, 0.5668],
     [0.1461, 0.5113],
     [0.2315, 0.3788],
     [0.0494, 0.5590],
     [0.1107, 0.4799],
     [0.1121, 0.5735],
     [0.1007, 0.6318],
     [0.2567, 0.4326],
     [0.1956, 0.4280]   
    ]
 
#输出数据集
print (X)

"""
第二部分：KMeans聚类
clf = KMeans(n_clusters=3) 表示类簇数为3，聚成3类数据，clf即赋值为KMeans
y_pred = clf.fit_predict(X) 载入数据集X，并且将聚类的结果赋值给y_pred
"""

clf = KMeans(n_clusters=3)
y_pred = clf.fit_predict(X)
 
#输出完整Kmeans函数，包括很多省略参数
print(clf)
#输出聚类预测结果
print("y_pred = ",y_pred)
 
"""
第三部分：可视化绘图
"""

import numpy as np
import matplotlib.pyplot as plt

#获取数据集的第一列和第二列数据 使用for循环获取 n[0]表示X第一列
x = [n[0] for n in X]
print (x)
y = [n[1] for n in X]
print (y)

''' 
绘制散点图 
参数：x横轴; y纵轴; c=y_pred聚类预测结果; marker类型:o表示圆点,*表示星型,x表示点;
'''
plt.scatter(x, y, c=y_pred, marker='x')
 
#绘制标题
plt.title("Kmeans-Basketball Data")
 
#绘制x轴和y轴坐标
plt.xlabel("assists_per_minute")
plt.ylabel("points_per_minute")
 
#设置右上角图例
plt.legend(["A","B","C"])
 
#显示图形
plt.show()

第一段代码是对灰度图做聚类，同样我们还可以对多通道图像做聚类分析

# coding: utf-8
import cv2
import numpy as np
import matplotlib.pyplot as plt

#读取原始图像
img = cv2.imread('lenna.png') 
print (img.shape)

#图像二维像素转换为一维
data = img.reshape((-1,3))
data = np.float32(data)

#停止条件 (type,max_iter,epsilon)
criteria = (cv2.TERM_CRITERIA_EPS +
            cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)

#设置标签
flags = cv2.KMEANS_RANDOM_CENTERS

#K-Means聚类 聚集成2类
compactness, labels2, centers2 = cv2.kmeans(data, 2, None, criteria, 10, flags)

#K-Means聚类 聚集成4类
compactness, labels4, centers4 = cv2.kmeans(data, 4, None, criteria, 10, flags)

#K-Means聚类 聚集成8类
compactness, labels8, centers8 = cv2.kmeans(data, 8, None, criteria, 10, flags)

#K-Means聚类 聚集成16类
compactness, labels16, centers16 = cv2.kmeans(data, 16, None, criteria, 10, flags)

#K-Means聚类 聚集成64类
compactness, labels64, centers64 = cv2.kmeans(data, 64, None, criteria, 10, flags)

#图像转换回uint8二维类型
centers2 = np.uint8(centers2)
res = centers2[labels2.flatten()]
dst2 = res.reshape((img.shape))

centers4 = np.uint8(centers4)
res = centers4[labels4.flatten()]
dst4 = res.reshape((img.shape))

centers8 = np.uint8(centers8)
res = centers8[labels8.flatten()]
dst8 = res.reshape((img.shape))

centers16 = np.uint8(centers16)
res = centers16[labels16.flatten()]
dst16 = res.reshape((img.shape))

centers64 = np.uint8(centers64)
res = centers64[labels64.flatten()]
dst64 = res.reshape((img.shape))

#图像转换为RGB显示
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
dst2 = cv2.cvtColor(dst2, cv2.COLOR_BGR2RGB)
dst4 = cv2.cvtColor(dst4, cv2.COLOR_BGR2RGB)
dst8 = cv2.cvtColor(dst8, cv2.COLOR_BGR2RGB)
dst16 = cv2.cvtColor(dst16, cv2.COLOR_BGR2RGB)
dst64 = cv2.cvtColor(dst64, cv2.COLOR_BGR2RGB)

#用来正常显示中文标签
plt.rcParams['font.sans-serif']=['SimHei']

#显示图像
titles = [u'原始图像', u'聚类图像 K=2', u'聚类图像 K=4',
          u'聚类图像 K=8', u'聚类图像 K=16',  u'聚类图像 K=64']  
images = [img, dst2, dst4, dst8, dst16, dst64]  
for i in range(6):  
   plt.subplot(2,3,i+1), plt.imshow(images[i], 'gray'), 
   plt.title(titles[i])  
   plt.xticks([]),plt.yticks([])  
plt.show()

结果：

优点：
1.是解决聚类问题的一种经典算法，简单、快速
2.对处理大数据集，该算法保持高效率
3.当结果簇是密集的，它的效果较好

缺点：
1.必须事先给出k（要生成的簇的数目，可通过多次实验得出）。
2.对躁声和孤立点数据敏感

三. 层次聚类

层次聚类是一种很直观的算法。顾名思义就是要一层一层地进行聚类。

层次法（Hierarchicalmethods）先计算样本之间的距离。每次将距离最近的点合并到同一个类。然后，再计算类与类之间的距离，将距离最近的类合并为一个大类。不停的合并，直到合成了一个类。而我们要用到的就是这个聚类过程中的中间过程。其中类与类的距离的计算方法有：最短距离法，最长距离法，中间距离法，类平均法等。比如最短距离法，将类与类的距离定义为类与类之间样本的最短距离。

层次聚类算法根据层次分解的顺序分为：自下底向上和自上向下，即凝聚的层次聚类算法和分裂的层次聚类算法（agglomerative和divisive），也可以理解为自下而上法（bottom-up）和自上而下法（top- down）。

凝聚层次聚类的流程

凝聚型层次聚类的策略是先将每个对象作为一个簇，然后合并这些原子簇为越来越大的簇，直到所有对象都在一个簇中，或者某个终结条件被满足。绝大多数层次聚类属于凝聚型层次聚类，它们只是在簇间相似度的定义上有所不同。 这里给出采用最小距离的凝聚层次聚类算法流程：

(1) 将每个对象看作一类，计算两两之间的最小距离；

(2) 将距离最小的两个类合并成一个新类；

(3) 重新计算新类与所有类之间的距离；

(4) 重复(2)、(3)，直到所有类最后合并成一类。

特点：

• 凝聚的层次聚类并没有类似K均值的全局目标函数，没有局部极小问题或是很难选择初始点的问题。
• 合并的操作往往是最终的，一旦合并两个簇之后就不会撤销。
• 当然其计算存储的代价是昂贵的。

下面举例说明

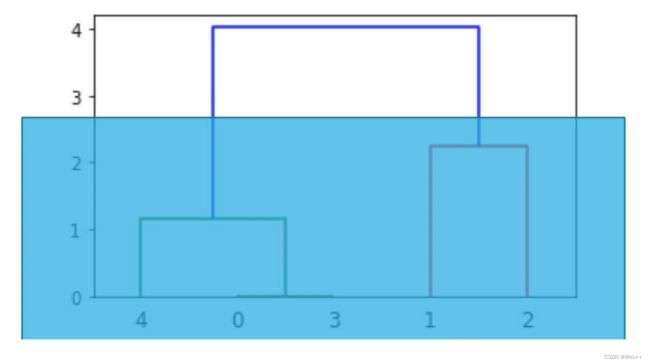
如图为层次聚类的一个过程图
横轴：数据序号
纵轴：合并序号
代码：
这里首先0号和3号进行合并，距离为0， 这个类里面有2个样本

上图为层次聚类的结果

第三行、第四行以此类推
因为类别5有两个样本，加上类别4形成类别6，有3个样本；
类别7是类别1、2聚类形成，有两个样本；
类别6、7聚成一类后，类别8有5个样本，这样X全部样本参与聚类，聚类完成。
Z第四列中有样本的个数，当最下面一行中的样本数达到样本总数时，聚类就完成了。
树状图分类判断
想分两类时，就从上往下数有两根竖线时进行切割，那么所对应的竖线下面所连接的为一类

想分三类时，就从上往下数有三根竖线时进行切割，那么所对应的竖线下面所连接的为一类

代码实现

###cluster.py
#导入相应的包
from scipy.cluster.hierarchy import dendrogram, linkage,fcluster
from matplotlib import pyplot as plt

'''
linkage(y, method=’single’, metric=’euclidean’) 共包含3个参数: 
1. y是距离矩阵,可以是1维压缩向量（距离向量），也可以是2维观测向量（坐标矩阵）。
若y是1维压缩向量，则y必须是n个初始观测值的组合，n是坐标矩阵中成对的观测值。
2. method是指计算类间距离的方法。

'''
'''
fcluster(Z, t, criterion=’inconsistent’, depth=2, R=None, monocrit=None) 
1.第一个参数Z是linkage得到的矩阵,记录了层次聚类的层次信息; 
2.t是一个聚类的阈值-“The threshold to apply when forming flat clusters”。
'''

X = [[1,2],[3,2],[4,4],[1,2],[1,3]]
Z = linkage(X, 'ward')
f = fcluster(Z,4,'distance')
fig = plt.figure(figsize=(5, 3))
dn = dendrogram(Z)
print(Z)
plt.show()

总结：
层次聚类的优缺点

优点：
1，距离和规则的相似度容易定义，限制少；
2，不需要预先制定聚类数；
3，可以发现类的层次关系；

缺点：
1，计算复杂度太高；
2，算法很可能聚类成链状
计算复杂度高是一个很大的缺点，因为这会导致对硬件的要求非常高，有些硬件，比如手机，我要用手机来存储层次聚类过程中的数据，那肯定是不太合理的。而K - Means聚类的缺点是在于要设置 k 值，但是它对硬件的要求没多高，所以说虽然层次聚类虽然解决了要预先设定k值的缺点，但是对硬件的要求变得很苛刻。所以在工程项目中，K - Means要比层次聚类用得更多。

每一种聚类方法都有其特定的数据结构，对于服从高斯分布的数据用K-Means来进行聚类效果 会比较好。
而对于类别之间存在层结构（比如大学成绩）的数据，用层次聚类会比较好。

四. 密度聚类

密度聚类DBSCAN

算法:

需要两个参数：ε (eps) 和形成高密度区域所需要的最少点数 (minPts)

• 它由一个任意未被访问的点开始，然后探索这个点的 ε-邻域，如果 ε-邻域里有足够的点，则建立一个新的聚类，否则这个点被标签为杂音。
• 注意，这个杂音点之后可能被发现在其它点的 ε-邻域里，而该 ε-邻域可能有足够的点，届时这个点会被加入该聚类中。

优点：

1. 对噪声不敏感；

缺点：

1. 聚类的结果与参数有很大的关系（参数很难选取）；

代码实现

import matplotlib.pyplot as plt  
import numpy as np  
from sklearn import datasets 
from  sklearn.cluster import DBSCAN
 
iris = datasets.load_iris() 
X = iris.data[:, :4]  # #表示我们只取特征空间中的4个维度
print(X.shape)
# 绘制数据分布图
'''
plt.scatter(X[:, 0], X[:, 1], c="red", marker='o', label='see')  
plt.xlabel('sepal length')  
plt.ylabel('sepal width')  
plt.legend(loc=2)  
plt.show()  
'''

dbscan = DBSCAN(eps=0.4, min_samples=9)
dbscan.fit(X) 
label_pred = dbscan.labels_
 
# 绘制结果
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
x2 = X[label_pred == 2]
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label0')  
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label1')  
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label2')  
plt.xlabel('sepal length')  
plt.ylabel('sepal width')  
plt.legend(loc=2)  
plt.show()  

五. 拓展 ---- 谱聚类

扩展 — 谱聚类

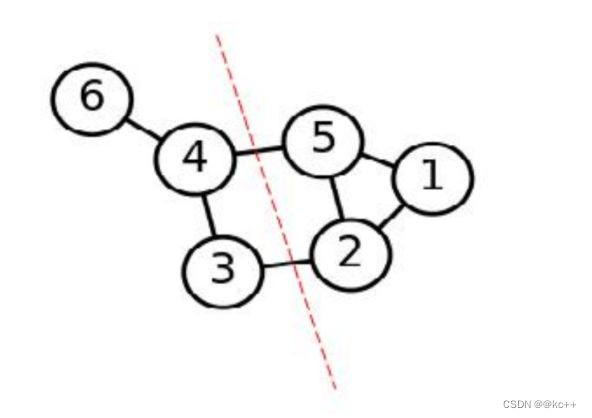
1. 根据数据构造一个 图结构（Graph） ，Graph 的每一个节点对应一个数据点，将相似的点连接起来，并且边的权重用于表示数据之间的相似度。把这个 Graph 用邻接矩阵的形式表示出来，记为 W 。
2. 把 W 的每一列元素加起来得到 N 个数，把它们放在对角线上（其他地方都是零），组成一个 N * N的矩阵，记为 D 。并令 L = D-W 。
3. 求出 L 的前 k 个特征值，以及对应的特征向量。
4. 把这 k 个特征（列）向量排列在一起组成一个 N * k 的矩阵，将其中每一行看作 k维空间中的一个向量，并使用 K-means 算法进行聚类。聚类的结果中每一行所属的类别就是原来 Graph 中的节点亦即最初的N 个数据点分别所属的类别。

简单抽象谱聚类过程，主要有两步：

1. 构图，将采样点数据构造成一张网图。
2. 切图，即将第一步构造出来的按照一定的切边准则，切分成不同的图，而不同的子图，即我们对应的聚类结果。