求若干时间点的气温值问题——分段线性和分段三次插值

分别用分段线性和分段三次插值，求气温对时间的函数（Python程序，含可视化结果）

问题描述：
在凌晨1点至中午12点，每隔1小时测量一次温度为：[5，8，9，15，25，29，31， 30，22，25，27，24]；预测时间为 3.2，5.6，7.8，11.5时的温度。

测试用例：
温度：[5，8，9，15，25，29，31， 30，22，25，27，24]；
时间： 3.2，5.6，7.8，11.5。

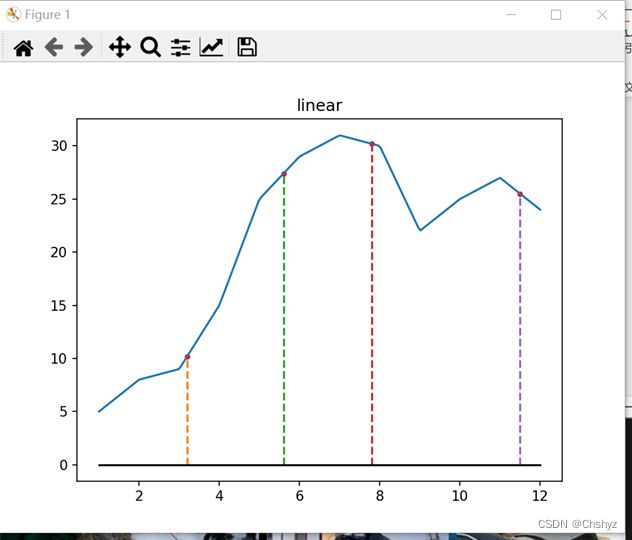
1、分段线性插值算法实现：

import numpy as np
#import matplotlib
#matplotlib.use('Qt5Agg')
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d
X = np.arange(1, 13)
Y = np.array([5, 8, 9, 15, 25, 29, 31, 30, 22, 25, 27, 24])
f = interp1d(X, Y, 'linear')
print('预测值:')
PX, PY = [], []
for t in [3.2, 5.6, 7.8, 11.5]:
    print('时间：%4.1f  温度：%4.1f' % (t, f(t)))
    PX.append(t)
    PY.append(f(t))
    plt.plot([t, t], [0, f(t)], '--')
plt.scatter(PX, PY, marker='.', color='r')
plt.plot([1, 12], [0, 0], 'k')
plt.show()

测试结果：

2、分段三次插值算法实现：

import numpy as np
#import matplotlib
#matplotlib.use('Qt5Agg')
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d

X = np.arange(1, 13)
Y = np.array([5, 8, 9, 15, 25, 29, 31, 30, 22, 25, 27, 24])
f = interp1d(X, Y, 'cubic')

t = np.linspace(1, 12, 200)
plt.plot(t, f(t))
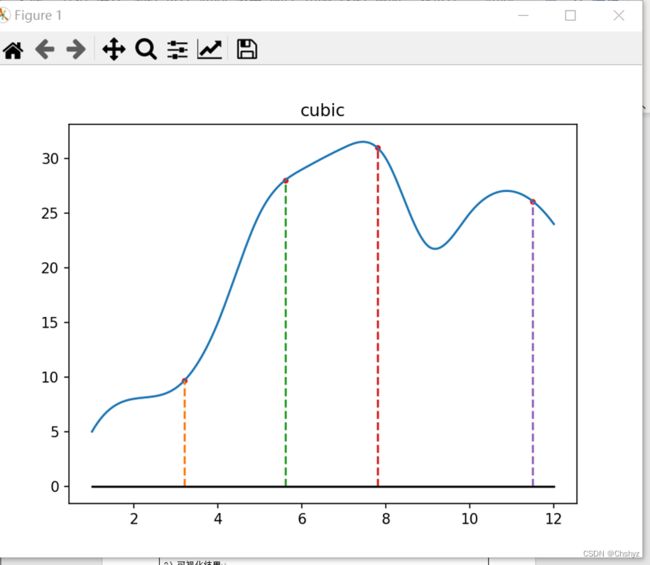
plt.title('cubic')

print('预测值:')
PX, PY = [], []
for t in [3.2, 5.6, 7.8, 11.5]:
    print('时间：%4.1f  温度：%4.1f' % (t, f(t)))
    PX.append(t)
    PY.append(f(t))
    plt.plot([t, t], [0, f(t)], '--')
plt.scatter(PX, PY, marker='.', color='r')
plt.plot([1, 12], [0, 0], 'k')
plt.show()

测试结果：

两种算法测试结果分析：
该问题分别使用了分段线性和分段三次插值，生成了一个连续的温度曲线，并且可以根据该曲线预测任意时间点的温度值。与线性插值相比，三次插值更加平滑，更能反映数据的变化趋势。预测值部分，程序预测了4个时间点的温度值，并将预测值标记在图中，方便用户进行查看和比较。可以看出，三次插值所得到的预测值相比线性插值更加平滑，更能反映真实的温度变化趋势。