【数字图像处理】【Matlab】【作业六】几何变换(平移、缩放、旋转、镜像、转置等)
注意事项:
1.使用软件:Matlab2019a。
2.使用图像来自网络。
3.所以坐标系均采用竖直为x轴,水平为y轴(与matlab矩阵对应)。
4.初学者代码仅供参考,可自行简化或添加自己想要的部分。
5.祝大家码代码快乐!
图像的几何变换
-
- 1.图像平移
-
- 1.1. 原理
- 1.2. 算法
- 1.3. 代码
- 1.4. 结果截图
- 2.图像缩放
-
- 2.1. 原理
- 2.3. 代码
- 2.4. 结果截图
- 3.图像旋转
-
- 3.1. 原理
- 3.3. 代码
- 3.4. 结果截图
- 4.图像镜像
-
- 4.1. 原理
- 4.2. 算法
- 4.3. 代码
- 4.4. 结果截图
- 5.图像转置
-
- 5.1. 原理
- 5.2. 算法
- 5.3. 代码
- 5.4. 结果截图
- 6.图像剪切
- 7.图像的整体切变
1.图像平移
1.1. 原理
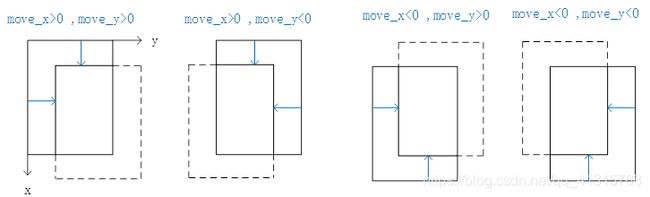
图像平移是将图像中所有的点都按照指定的平移量,进行水平、垂直移动。
设初始坐标为 ( x 0 , y 0 ) (x0,y0) (x0,y0)的点经过平移 ( t x , t y ) (tx,ty) (tx,ty)后坐标变为 ( x 1 , y 1 ) (x1,y1) (x1,y1)
{ x 1 = x 0 + t x y 1 = y 0 + t y \begin{cases}x1=x0+tx\\y1=y0+ty\end{cases} {x1=x0+txy1=y0+ty

1.2. 算法
-
获取原图像的宽高。
-
输入偏移量move_x,move_y。
-
新建一个同样大小的图像空白矩阵。
-
对原图依次循环每个像素,每读入一个像素点(x0,y0),根据它的坐标,找到目标图像的位置(x1=x0-move_x,y1=y0-move_y) ,将像素( x0,y0) 处的灰度值值赋给新图中的(x1,y1)。
1.3. 代码
【mymove.m】
% 函数mymove:实现图像的上下左右平移
% 输入参数:I为原图像
% move_x,move_y为竖直,水平位移大小
% 输出参数:平移变换后的图像OUT
% 使用函数:double(I):增大精度,便于图像的计算
% size(J):求矩阵的宽高
% zeros():生成全零矩阵
% inf:无穷大(白色)
function OUT = mymove(I,move_x,move_y)
J=double(I);
HW=size(J);%获取原图像大小
OUT=zeros(HW);%新建新的图像矩阵
OUT(1:HW(1),1:HW(2))=inf;%初始为全白图像
if((move_x>=0) && (move_y>=0))
OUT(move_x+1:HW(1),move_y+1:HW(2))=J(1:HW(1)-move_x,1:HW(2)-move_y);
elseif((move_x>0) && (move_y<0))
OUT(move_x+1:HW(1),1:HW(2)+move_y)=J(1:HW(1)-move_x,1-move_y:HW(2));
elseif((move_x<0) && (move_y>0))
OUT(1:HW(1)+move_x,move_y+1:HW(2))=J(1-move_x:HW(1),1:HW(2)-move_y);
elseif((move_x<0) && (move_y<0))
OUT(1:HW(1)+move_x,1:HW(2)+move_y)=J(1-move_x:HW(1),1-move_y:HW(2));
end
OUT=uint8(OUT);
end
【main.m】
%主函数
close all;
clear all; %#ok<*CLALL>
clc;
%% RGB->灰度图像
RGB=imread('test.png'); %图像读入
I=rgb2gray(RGB); %把 RGB 图像转换成灰度图像
%% 图像的平移(Image translation)
move_x=100;%竖直位移(默认向下)
move_y=60;%水平位移(默认向右)
OUT_1_1=mymove(I,move_x,move_y);
move_x=100;move_y=-60;
OUT_1_2=mymove(I,move_x,move_y);
move_x=-100;move_y=60;
OUT_1_3=mymove(I,move_x,move_y);
move_x=-100;move_y=-60;
OUT_1_4=mymove(I,move_x,move_y);
move_x=1050;move_y=-60;%超出图像范围的情况
OUT_1_5=mymove(I,move_x,move_y);
figure,suptitle('【图像平移】');
subplot(2,3,1),imshow(I),axis on,title('原图像');
subplot(2,3,2),imshow(OUT_1_1),axis on,title('平移变换1');
subplot(2,3,3),imshow(OUT_1_2),axis on,title('平移变换2');
subplot(2,3,4),imshow(OUT_1_3),axis on,title('平移变换3');
subplot(2,3,5),imshow(OUT_1_4),axis on,title('平移变换4');
subplot(2,3,6),imshow(OUT_1_5),axis on,title('平移变换5(平移距离超出原图像坐标范围)');
1.4. 结果截图
2.图像缩放
2.1. 原理
假设图像X轴方向缩放比率是 k x kx kx, Y轴方向缩放比率是 k y ky ky,
{ x 1 = x 0 ∗ k x y 1 = y 0 ∗ k y \begin{cases}x1=x0*kx\\y1=y0*ky\end{cases} {x1=x0∗kxy1=y0∗ky
当 k x > 1 kx>1 kx>1且 k y > 1 ky>1 ky>1时,原图像被放大。放大图像时, 产生了新的像素, 可通过插值算法来近似处理。
当 k x < 1 kx<1 kx<1且 k y < 1 ky<1 ky<1时,原图像被缩小。
当 k x = k y kx=ky kx=ky时,图象被等比例放缩;当 k x ≠ k y kx≠ky kx=ky时,图像被非比例放缩,图像会发生变形,且这种变形是不可逆转的。
2.2. 算法
-
获取原图像的宽高。
-
输入缩放比例:zoom_x,zoom_y。
-
得到新图像的宽度和高度。
-
每个目标点的坐标依次循环。计算该象素在原图像中的坐标,使用双线性插值算法,算出像素值赋给目标点。
-
最终输出放缩后的图像,无论是放大还是缩小,画布的大小都不变,这样更易观察图像的变换情况。
-
双线性插值算法具体步骤:
①先按要求缩放原图像,得出缩放后的坐标,再由缩放后的坐标 ( i , j ) (i,j) (i,j)求出该坐标在原图像上的位置,即 ( x , y ) = ( i z o o m x , j z o o m y ) (x,y)=(\frac{i}{zoom_x},\frac{j}{zoom_y}) (x,y)=(zoomxi,zoomyj),即为上图所示的M点 ( [ x ] + u , [ y ] + v ) ([x]+u,[y]+v) ([x]+u,[y]+v)。其中 ( u , v ) (u,v) (u,v)表示小数部分的坐标。
②设原图像中有4个点,分别为 R 1 ( a 1 , b 1 ) , R 2 ( a 1 , b 2 ) , R 3 ( a 2 , b 1 ) , R 4 ( a 2 , b 2 ) R1(a1,b1),R2(a1,b2),R3(a2,b1),R4(a2,b2) R1(a1,b1),R2(a1,b2),R3(a2,b1),R4(a2,b2),其中这四点为相邻点,即
a 2 − a 1 = 1 ; b 2 − b 1 = 1 ; a2-a1=1;b2-b1=1; a2−a1=1;b2−b1=1;
而图中M点([x]+u,[y]+v)为缩放图像所要插入的点。
③根据双线性插值的算法,先在x方向上进行线性插值,即有
{ f ( M 1 ) = u ∗ f ( R 1 ) + ( 1 − u ) ∗ f ( R 2 ) ; f ( M 2 ) = u ∗ f ( R 3 ) + ( 1 − u ) ∗ f ( R 4 ) ; \begin{cases}f(M1)=u*f(R1)+(1-u)*f(R2);\\ f(M2)=u*f(R3)+(1-u)*f(R4);\end{cases} {f(M1)=u∗f(R1)+(1−u)∗f(R2);f(M2)=u∗f(R3)+(1−u)∗f(R4);
④再在y方向上进行线性插值,即有
f ( M ) = v ∗ f ( M 1 ) + ( 1 − v ) ∗ f ( M 2 ) ; f(M)=v*f(M1)+(1-v)*f(M2); f(M)=v∗f(M1)+(1−v)∗f(M2);
⑤综上,有: f ( M ) = u v f ( R 1 ) + ( 1 − u ) v f ( R 2 ) + u ( 1 − v ) f ( R 3 ) + ( 1 − u ) ( 1 − v ) f ( R 4 ) ; f(M)=uvf(R1)+(1-u)vf(R2)+u(1-v)f(R3)+(1-u)(1-v)f(R4); f(M)=uvf(R1)+(1−u)vf(R2)+u(1−v)f(R3)+(1−u)(1−v)f(R4);
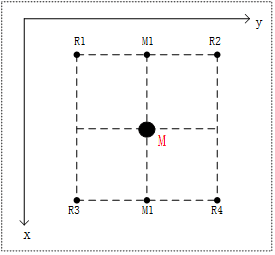
图2-1 图像缩放双线性插值法
2.3. 代码
目前myimresize存在问题:对于图像像素大小为奇数的图像无法处理!!暂未修改
【myimresize.m】
% 函数myimresize:采用双线性插值法对图像进行缩放处理
% 输入参数:I为原图像
% zoom_x,zoom_y表示缩放的倍数
% 输出参数:平移变换后的图像OUT
% 使用函数:floor(x):向下取整
% ceil(x):向上取整
% round(x):取最接近的整数
function OUT=myimresize(I,zoom_x,zoom_y)
J=double(I); %二维矩阵转为双精度类型
HW=size(J);%获取原图像大小
OUT=zeros(HW);%新建新的图像矩阵
OUT(1:HW(1),1:HW(2))=inf;%初始为空白
rHW=[round(HW(1)*zoom_y),round(HW(2)*zoom_x)];%新的图像高宽
for i = 1 : rHW(1) %缩放后的图像的(i,j)位置对应原图的(x,y)
for j = 1 : rHW(2)
x = i / zoom_y ;
y = j / zoom_x ;
u = x - floor(x);
v = y - floor(y); %得到小数部分坐标
if x < 1 %图像的边界处理
x = 1;
end
if y < 1
y = 1;
end
%用原图的四个真实像素点来双线性插值获得“虚”像素的像素值
OUT(i, j) = J(floor(x), floor(y)) * u * v + ...
J(floor(x), ceil(y)) * (1-u) * v + ...
J(ceil(x), floor(y)) * u * (1-v) + ...
J(ceil(x), ceil(y)) *(1-u) * (1-v);
end
end
OUT=uint8(OUT(1:HW(1),1:HW(2)));
end
【main.m】
%主函数
close all;
clear all; %#ok<*CLALL>
clc;
%% RGB->灰度图像
RGB=imread('test.png'); %图像读入
I=rgb2gray(RGB); %把 RGB 图像转换成灰度图像
%% 图像的缩放(Image scaling)
zoom_x=0.5;zoom_y=0.5;%等比缩小
OUT_2_1=myimresize(I,zoom_x,zoom_y);
zoom_x=2;zoom_y=2;%等比放大
OUT_2_2=myimresize(I,zoom_x,zoom_y);
zoom_x=0.5;zoom_y=0.8;%非比例缩小
OUT_2_3=myimresize(I,zoom_x,zoom_y);
zoom_x=1.8;zoom_y=1;%非比例放大
OUT_2_4=myimresize(I,zoom_x,zoom_y);
figure,suptitle('【图像缩放1】');
subplot(1,3,1),imshow(I),axis on,title('原图像')
subplot(1,3,2),imshow(OUT_2_1),axis on,title('等比缩小变换');
subplot(1,3,3),imshow(OUT_2_2),axis on,title('等比放大变换');
figure,suptitle('【图像缩放2】');
subplot(1,3,1),imshow(I),axis on,title('原图像')
subplot(1,3,2),imshow(OUT_2_3),axis on,title('非比例缩小变换');
subplot(1,3,3),imshow(OUT_2_4),axis on,title('非比例放大变换');
2.4. 结果截图
3.图像旋转
3.1. 原理
必须指明图像绕着什么旋转。 一般图像的旋转是以图像的中心为原点, 旋转一定的角度。
旋转后, 一般会改变图像的大小。
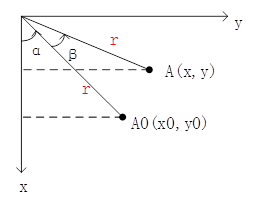
设原始图像的任意点A0(x0,y0)经逆时针旋转角度β以后到新的位置A(x,y),为表示方便,采用极坐标形式:
{ x 0 = r c o s ( β ) y 0 = r s i n ( β ) \begin{cases}x0=rcos(β)\\y0=rsin(β)\end{cases} {x0=rcos(β)y0=rsin(β)
逆时针旋转变换后的坐标为:
{ x 1 = x 0 c o s ( β ) − y 0 s i n ( β ) y 1 = x 0 s i n ( β ) + y 0 c o s ( β ) \begin{cases}x1=x0cos(β)-y0sin(β)\\y1=x0sin(β)+y0cos(β)\end{cases} {x1=x0cos(β)−y0sin(β)y1=x0sin(β)+y0cos(β)
变换如下图所示:
3.2. 算法
-
获取原图像的宽高。
-
输入旋转角度: a l p h a alpha alpha,进行如下处理:
①将旋转角度转换到0~360之间计算;
②得到旋转弧度;

图3-2 图像旋转角度范围 -
由此可将旋转角度分为以上4个区间,每个区间对应的变换不同。
-
得到新图像的宽度和高度。
为了确保旋转后的图像都能够在画布内,不会被切点,初始化的画布设置为最大,所以用到了 a b s ( x ) abs(x) abs(x)取绝对值和 c e i l ( x ) ceil(x) ceil(x)向上取整两个函数。
nHW(1)=ceil(HW(1)*abs(cos(abs(alpha)))+HW(2)*abs(sin(abs(alpha))));
nHW(2)=ceil(HW(1)*abs(sin(abs(alpha)))+HW(2)*abs(cos(abs(alpha))));
- 每个目标点的坐标依次循环。
①计算该象素在原图像中的坐标:
这个地方尤其注意由于我们默认设置为逆时针变换,而计算时是由新图像的坐标点 ( i , j ) (i,j) (i,j)换算出其在原图像所在的位置 ( x , y ) (x,y) (x,y)所以转换矩阵应该反过来才对,即转换矩阵如下:
{ x = i c o s ( β ) + j s i n ( β ) y = − i s i n ( β ) + j c o s ( β ) \begin{cases}x=icos(β)+jsin(β)\\y=-isin(β)+jcos(β)\end{cases} {x=icos(β)+jsin(β)y=−isin(β)+jcos(β)
为了使得到的图像都能显示在画布的正中心,根据角度 a l p h a alpha alpha的四个区间分为4种情况,每种情况的位移量不同,由此得到不同的4个计算公式。
②然后使用双线性插值算法,(具体步骤和图像缩放时的一样)算出像素值赋给目标点。 - 最终输出放缩后的图像,无论是放大还是缩小,画布的大小都不变,这样更易观察图像的变换情况。
3.3. 代码
【myimrotate.m】
%函数myimrotate:采用双线性插值法实现图像旋转
%输入参数:I原图像
% alpha:旋转的角度(>0为逆时针)
%输出参数:OUT旋转变换后的图像
%使用函数:mod(m,n):对m/n取余
% abs(x):取绝对值
% ceil(x):向上取整
% pi:3.1415926......可直接使用
% floor(x):向下取整
function OUT=myimrotate(I,alpha)
J=double(I);
HW=size(J);%获取原图像大小
alpha=mod(alpha,360);%将旋转角度转换到0~360之间计算
alpha=alpha*pi/180;%得到旋转弧度
%确保旋转后的图片还在坐标系内
nHW(1)=ceil(HW(1)*abs(cos(abs(alpha)))+HW(2)*abs(sin(abs(alpha))));%新图像的高heighth
nHW(2)=ceil(HW(1)*abs(sin(abs(alpha)))+HW(2)*abs(cos(abs(alpha))));%新图像的宽width
OUT=zeros(nHW);%新建新的图像矩阵
OUT(1:nHW(1),1:nHW(2))=inf;%初始为空白
u0=HW(2)*sin(alpha);u2=HW(1)*cos(alpha);%竖直方向的相关平移量
u1=HW(1)*sin(alpha);u3=HW(2)*cos(alpha);%水平方向的相关平移量
T=[cos(alpha),sin(alpha);-sin(alpha),cos(alpha)];%变换矩阵
for i = 1:nHW(1)%(i,j)是新图像坐标,变换到原图像坐标(x,y)中。
for j=1:nHW(2)
if(alpha>=0 && alpha<=pi/2)
XY=T*([i;j]-[u0;0]);%保证输出在图像的中心
elseif(alpha>pi/2 && alpha<=pi)
XY=T*([i;j]-[u0-u2;-u3]);%保证输出在图像的中心
elseif(alpha>pi && alpha<=3*pi/2)
XY=T*([i;j]-[-u2;-u3-u1]);%保证输出在图像的中心
elseif(alpha>3*pi/2 && alpha<=2*pi)
XY=T*([i;j]-[0;-u1]);%保证输出在图像的中心
end
x=XY(1);%变换得到的原坐标
y=XY(2);
if x>=1 && x<=HW(1) && y>=1 && y<=HW(2) %若变换出的x和y在原图像范围内
u = x - floor(x);
v = y - floor(y); %得到小数部分坐标
%用原图的四个真实像素点来双线性插值获得“虚”像素的像素值
OUT(i, j) = J(floor(x), floor(y)) * u * v + ...
J(floor(x), ceil(y)) * (1-u) * v + ...
J(ceil(x), floor(y)) * u * (1-v) + ...
J(ceil(x), ceil(y)) *(1-u) * (1-v);
end
end
end
OUT=uint8(OUT);
end
【main.m】
%主函数
close all;
clear all;
clc;
%% RGB->灰度图像
RGB=imread('test.png'); %图像读入
I=rgb2gray(RGB); %把 RGB 图像转换成灰度图像
%% 图像的旋转(Image rotation)
alpha=30;%默认>0为逆时针旋转
OUT_2_1=myimrotate(I,alpha);
alpha=120;
OUT_2_2=myimrotate(I,alpha);
alpha=-30;%默认<0为顺时针旋转
OUT_2_3=myimrotate(I,alpha);
alpha=-100;
OUT_2_4=myimrotate(I,alpha);
figure,suptitle('【图像逆时针旋转】');
subplot(1,3,1),imshow(I),axis on,title('原图像');
subplot(1,3,2),imshow(OUT_2_1),axis on,title('图像旋转1');
subplot(1,3,3),imshow(OUT_2_2),axis on,title('图像旋转2');
figure,suptitle('【图像顺时针旋转】');
subplot(1,3,1),imshow(I),axis on,title('原图像');
subplot(1,3,2),imshow(OUT_2_3),axis on,title('图像旋转3');
subplot(1,3,3),imshow(OUT_2_4),axis on,title('图像旋转4');
3.4. 结果截图
4.图像镜像
4.1. 原理
分为两种:一种是水平镜像,另一种是垂直镜像。
设图像高度为 H e i g h t Height Height, 宽度为 W i d t h Width Width;
图像的水平镜像操作是以原图像的垂直中轴线为中心,将图像分为左右两部分进行对称变换;
{ x 1 = x 0 y 1 = w i d t h + 1 − y 0 \begin{cases}x1=x0\\y1=width+1-y0\end{cases} {x1=x0y1=width+1−y0
图像的垂直镜像操作是以原图像的水平中轴线为中心,将图像分为上下两部分进行对称变换。
{ x 1 = h e i g h t + 1 − x 0 y 1 = y 0 \begin{cases}x1=height+1-x0\\y1=y0\end{cases} {x1=height+1−x0y1=y0
镜像变换后图的高和宽都不变。
4.2. 算法
- 获取原图像的宽高。
- 输入choice。
- 新建一个同样大小的图像空白矩阵。
- 根据choice选择是水平镜像还是垂直镜像。
4.3. 代码
【mymirror.m】
%函数mymirror:实现图像镜像
%输入参数:I原图像
% choice选择水平或垂直镜像
%输出参数:OUT镜像变换后的图像
%使用函数:strcmp(a,b):比较两个字符串是否相等
function OUT=mymirror(I,choice)
J=double(I);
HW=size(J);%获取原图像大小
OUT=zeros(HW);%新建新的图像矩阵
OUT(1:HW(1),1:HW(2))=inf;%初始为空白
for i = 1:HW(1)
for j=1:HW(2)
if strcmp(choice,'level')
OUT(i, j) = J(i, HW(2)+1-j);
elseif strcmp(choice,'vertical')
OUT(i, j) = J(HW(1)+1-i, j);
end
end
end
OUT=uint8(OUT);
end
【main.m】
%主函数
close all;
clear all; %#ok<*CLALL>
clc;
%% RGB->灰度图像
RGB=imread('test.png'); %图像读入
I=rgb2gray(RGB); %把 RGB 图像转换成灰度图像
%% 4.图像的镜像变换(Image mirror transformation)
OUT_4_1=mymirror(I,'level');%选择参数'level'即为水平镜像
OUT_4_2=mymirror(I,'vertical');%选择参数'vertical'即为垂直镜像
figure,suptitle('【图像镜像变换】');
subplot(1,3,1),imshow(I),axis on,title('原图像');
subplot(1,3,2),imshow(OUT_4_1),axis on,title('水平镜像');
subplot(1,3,3),imshow(OUT_4_2),axis on,title('垂直镜像');
4.4. 结果截图
5.图像转置
5.1. 原理
将图像像素的x坐标和y坐标互换。 将改变图像的高度和宽度,转置后图像的高度和宽度将互换。
{ x 1 = y 0 y 1 = x 0 \begin{cases}x1=y0\\y1=x0\end{cases} {x1=y0y1=x0
5.2. 算法
- 获取原图像的宽高。
- 新建一个同样大小的图像空白矩阵。
- 将原图像转置后对应的点赋值给新图像的点。
5.3. 代码
【mytranspose.m】
%函数mytranspose:实现图像转置
%输入参数:I原图像
%输出参数:OUT转置变换后的图像
function OUT=mytranspose(I)
J=double(I);
HW=size(J);%获取原图像大小
OUT=zeros(HW(2),HW(1));%新建新的图像矩阵
OUT(1:HW(2),1:HW(1))=inf;%初始为空白
for i = 1:HW(2)
for j=1:HW(1)
OUT(i, j) = J(j,i);
end
end
OUT=uint8(OUT);
end
【main.m】
%主函数
close all;
clear all; %#ok<*CLALL>
clc;
%% RGB->灰度图像
RGB=imread('test.png'); %图像读入
I=rgb2gray(RGB); %把 RGB 图像转换成灰度图像
%% 5.图像的转置(Image transpose)
OUT_5_1=mytranspose(I);
figure,suptitle('【图像转置变换】');
subplot(1,2,1),imshow(I),axis on,title('原图像');
subplot(1,2,2),imshow(OUT_5_1),axis on,title('转置变换');
5.4. 结果截图
6.图像剪切
很简单!
J=double(I);
OUT_6=J(500:1000,200:300);
OUT_6=uint8(OUT_6);
7.图像的整体切变
id=maketform('affine',[1 4 0;2 1 0;0 0 1]');%创建图像整体切变参数结构体
id=imtransform(i,id,'FillValues',255);%实现图像整体切变
(使用 m a k e t f o r m maketform maketform也可以实现以上其他变换,大家可自行尝试)
好了,本次学习就到这里,嘻嘻~~码代码去了