数据结构 稀疏矩阵的实现方法

稀疏矩阵的实现

什么是稀疏矩阵，怎么定义才是稀疏矩阵?假设在m x n的矩阵中，有t个不为0的元素。令z=t/(m x n),若z<=0.05则称此矩阵为稀疏矩阵。由于稀疏矩阵的非0元素较少，所以如果用大容量存储必定会造成内存浪费，因此只需存储非0元素值即可，以下列出了常用的三种存储稀疏矩阵的方法。

三元组顺序表

三元组顺序表的实现用顺序存储结构来实现。定义一个数组的结构体，存储的是三元组（即由 3 部分数据组成的集合），组中数据分别表示（行标，列标，元素值）。结构体的实现如下：

//三元组结构体
typedef struct {
    int i,j;//行标i，列标j
    int data;//元素值
}triple;
//矩阵的结构表示
typedef struct {
    triple data[number];//存储该矩阵中所有非0元素的三元组
    int n,m,num;//n和m分别记录矩阵的行数和列数，num记录矩阵中所有的非0元素的个数
}TSMatrix;

如上图所示即为依次再数组中插入的 三元表。具体实现过程如下所示：

#include 
#define MAXSIZE 100
#define OK 1
#define ERROR 0
#define ELEMTYPE int

typedef struct {
	int i;   //行
	int j;   //列
	ELEMTYPE e; //元素
}Triple;
typedef struct {
	Triple data[MAXSIZE+1];
	int mu, nu, tu;
}TSmatrix;
void display(TSmatrix *s);
int main(void)
{
	TSmatrix s;
	s.mu = 3;
	s.nu = 3;
	s.tu = 3;
	s.data[0].i = 3;
	s.data[0].j = 3;
	s.data[0].e = 6;
	s.data[1].i = 2;
	s.data[1].j = 3;
	s.data[1].e = 8;
	s.data[2].i = 2;
	s.data[2].j = 1;
	s.data[2].e = 4;
	display(&s);
	getchar();
	return 0;
}

void display(TSmatrix *s)
{
	for (int i = 1; i <= s->mu; i++)
	{
		for (int j = 1; j <= s->nu; j++)
		{
			int value = 0;            //用来判断是否到了指定的（i,j）位置
			for (int k = 0; k < s->tu; k++)//遍历数组中的三元表值
			{
				if (s->data[k].i == i && s->data[k].j == j) //若遍历至指定（i,j）就打印元素值
				{
					value = 1;
					printf("%d ", s->data[k].e);
					break;
				}
			}
			if(value==0)  //若不为三元表中存储的值就打印0
			printf("%d ", 0);
		
		}
		printf("\n");
	}
}

结果如上图所示，检查矩阵可知打印的位置是没有问题的。
如上所示的方法能够实现稀疏矩阵的存储，但是在数据提取方面效率比较低，现在只是3x3的矩阵可能看不出来，但若是m和n都以千万计的情况下稀疏矩阵中的非0元素个数近似于n，那么时间复杂度就会达到O（m x n xn），这将非常浪费时间。因此在此方法上改进有了下面的方法。

行逻辑链接的顺序表

行逻辑链接顺序表示基于上种方法的改进，在上面的基础上再增加一个数组用来存储用来用于存储三元表的数组中每一行第一个非0元素的位置，这样就无需遍历整个三元表数组，只需要遍历对应行的数据就可以了，大大提高了效率。


使用数组 rpos 记录矩阵中每行第一个非 0 元素在一维数组中的存储位置。遍历的具体过程如下所示：
由 rpos 数组可知，第一行首个非 0 元素位于data[1]，因此在遍历此行时，可以直接从第 data[1] 的位置开始，一直遍历到下一行首个非 0 元素所在的位置（data[3]之前；
同样遍历第二行时，由 rpos 数组可知，此行首个非 0 元素位于 data[3]，因此可以直接从第 data[3] 开始，一直遍历到下一行首个非 0 元素所在的位置（data[4]）之前；
遍历第三行时，由 rpos 数组可知，此行首个非 0 元素位于 data[4]，由于这是矩阵的最后一行，因此一直遍历到 rpos 数组结束即可（也就是 data[tu]，tu 指的是矩阵非 0 元素的总个数）。

#include 
#define MAXSIZE 100
#define MAXSD  100
#define ELEMTYPE int

typedef struct {
	int i;
	int j;
	ELEMTYPE e;
}Triple;
typedef struct {
	Triple data[MAXSIZE];
	int rpos[MAXSD];  //定义rpos数组用于存储每一行第一个非0元素
	int mu, nu, tu;
}RLSmatrix;
void display(RLSmatrix *s);
int main(void)
{
	RLSmatrix s;
	s.mu = 4;
	s.nu = 3;
	s.tu = 4;

	s.data[1].i = 1;
	s.data[1].j = 1;
	s.data[1].e = 3;
	s.data[2].i = 2;
	s.data[2].j = 2;
	s.data[2].e = 4;
	s.data[3].i = 3;
	s.data[3].j = 3;
	s.data[3].e = 6;
	s.data[4].i = 4;
	s.data[4].j = 3;
	s.data[4].e = 3;

	s.rpos[1] = 1;
	s.rpos[2] = 2;
	s.rpos[3] = 3;
	s.rpos[4] = 4;
	display(&s);
	getchar();
	return 0;

}

void display(RLSmatrix *s)
{
	for (int i = 1; i <= s->mu; i++)
	{
		for (int j = 1; j <= s->nu; j++)
		{
			int value = 0;
			if(i+1<=s->mu) //假设一共i行则前面的i-1行遍历对应行的元素
			{
				for (int k = s->rpos[i]; k < s->rpos[i + 1]; k++) //遍历数组中对应行的非0元素即可
				{
					if (s->data[k].i == i && s->data[k].j == j) 
					{
						value = 1;
						printf("%d ", s->data[k].e);
						break;
					}
					if (value == 0)
						printf("0 ");
				}
			}
			else  //最后一行只需遍历到最后一个非0元素即可
			{
				for (int k = s->rpos[i]; k <=s->tu; k++)
				{
					if (s->data[k].i == i && s->data[k].j == j)
					{
						value = 1;
						printf("%d ", s->data[k].e);
						break;
					}
					if (value == 0)
						printf("0 ");
				}
			}
			
		}
		printf("\n");
	}
}

十字链表法存储稀疏矩阵

上面两种存储方式用于固定存储时可以很好的起作用，但是当要涉及非0元素的插入或者删除的时候回引起元素值的移动，例如两矩阵相加的操作，这种时候用链式存储表示三元组更为恰当，该存储方式采用的是 “链表+数组” 结构。


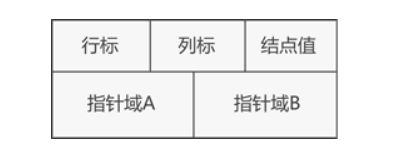
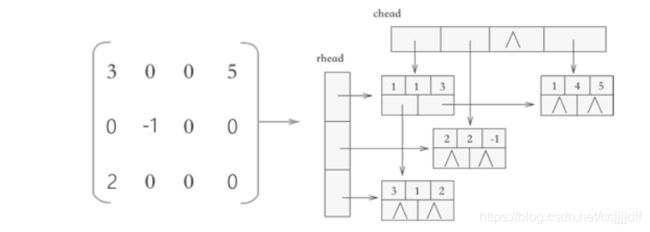
由上图可以看到，非0元素用一个含有五个域的节点表示，两个指针与分别用来指向同一列和同一行的元素。再用两个存储行链表和列链表的一维数组存储这些链表。每一个非0元既是某行链表的一个节点，又是列链表的一个节点。整个矩阵构成了一个十字交叉的链表。

#include
#include
typedef struct OLNode
{
    int i, j, e; //矩阵三元组i代表行 j代表列 e代表当前位置的数据
    struct OLNode *right, *down; //指针域 右指针 下指针
}OLNode, *OLink;
typedef struct
{
    OLink *rhead, *chead; //行和列链表头指针
    int mu, nu, tu;  //矩阵的行数,列数和非零元的个数
}CrossList;
CrossList CreateMatrix_OL(CrossList M);
void display(CrossList M);
int main()
{
    CrossList M;
    M.rhead = NULL;
    M.chead = NULL;
    M = CreateMatrix_OL(M);
    printf("输出矩阵M:\n");
    display(M);
    return 0;
}
CrossList CreateMatrix_OL(CrossList M)
{
    int m, n, t;
    int i, j, e;
    OLNode *p, *q;
    printf("输入矩阵的行数、列数和非0元素个数：");
    scanf("%d%d%d", &m, &n, &t);
    M.mu = m;
    M.nu = n;
    M.tu = t;
    if (!(M.rhead = (OLink*)malloc((m + 1) * sizeof(OLink))) || !(M.chead = (OLink*)malloc((n + 1) * sizeof(OLink))))
    {
        printf("初始化矩阵失败");
        exit(0);
    }
    for (i = 1; i <= m; i++)
    {
        M.rhead[i] = NULL;
    }
    for (j = 1; j <= n; j++)
    {
        M.chead[j] = NULL;
    }
    for (scanf("%d%d%d", &i, &j, &e); 0 != i; scanf("%d%d%d", &i, &j, &e)) {
        if (!(p = (OLNode*)malloc(sizeof(OLNode))))
        {
            printf("初始化三元组失败");
            exit(0);
        }
        p->i = i;
        p->j = j;
        p->e = e;
        //链接到行的指定位置
        if (NULL == M.rhead[i] || M.rhead[i]->j > j)
        {
            p->right = M.rhead[i];
            M.rhead[i] = p;
        }
        else
        {
            for (q = M.rhead[i]; (q->right) && q->right->j < j; q = q->right);
            p->right = q->right;
            q->right = p;
        }
        //链接到列的指定位置
        if (NULL == M.chead[j] || M.chead[j]->i > i)
        {
            p->down = M.chead[j];
            M.chead[j] = p;
        }
        else
        {
            for (q = M.chead[j]; (q->down) && q->down->i < i; q = q->down);
            p->down = q->down;
            q->down = p;
        }
    }
    return M;
}
void display(CrossList M) {
    for (int i = 1; i <= M.nu; i++)
    {
        if (NULL != M.chead[i])
        {
            OLink p = M.chead[i];
            while (NULL != p)
            {
                printf("%d\t%d\t%d\n", p->i, p->j, p->e);
                p = p->down;
            }
        }
    }
}