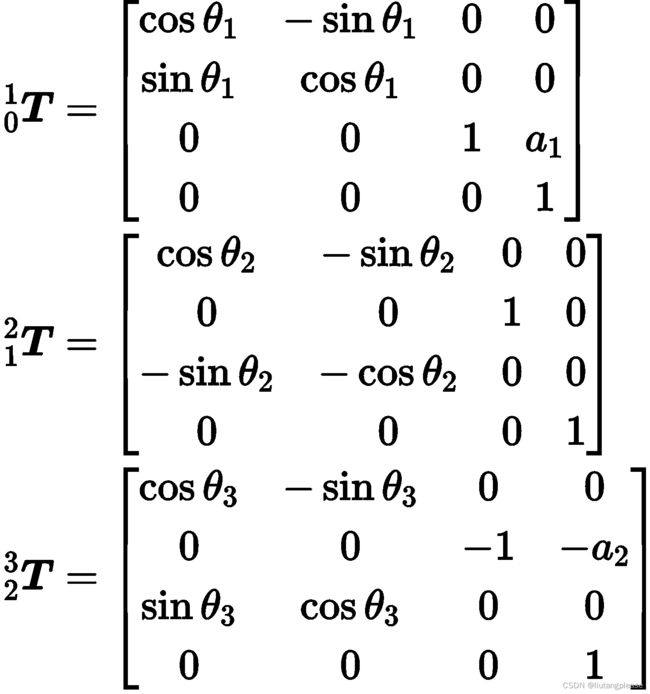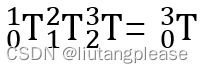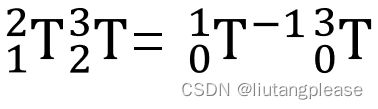机械臂速成小指南（二十三）：Paul方法求解机械臂运动学逆解（含matlab代码）
需要机械臂相关资源的同学可以在评论区中留言哦
指南目录：
机械臂速成小指南（零点五）：机械臂相关资源
机械臂速成小指南（零）：指南主要内容及分析方法
机械臂速成小指南（一）：机械臂发展概况
机械臂速成小指南（二）：机械臂的应用
机械臂速成小指南（三）：机械臂的机械结构
机械臂速成小指南（四）：机械臂关键部件之减速机
机械臂速成小指南（五）：末端执行器
机械臂速成小指南（六）：步进电机驱动器
机械臂速成小指南（七）：机械臂位姿的描述方法
机械臂速成小指南（八）：运动学建模（标准DH法）
机械臂速成小指南（九）：正运动学分析
机械臂速成小指南（十）：可达工作空间
机械臂速成小指南（十一）：坐标系的标准命名
机械臂速成小指南（十二）：逆运动学分析
机械臂速成小指南（十三）：轨迹规划概述
机械臂速成小指南（十四）：多项式插值轨迹规划
机械臂速成小指南（十五）：线性规划
机械臂速成小指南（十六）：带抛物线过渡的线性规划
机械臂速成小指南（十七）：直线规划
机械臂速成小指南（十八）：圆弧规划
机械臂速成小指南（十九）：机械臂的电路板抓取实验
机械臂速成小指南（二十）：机械臂的位姿重复性实验
机械臂速成小指南（二十一）：几何雅可比矩阵
机械臂速成小指南（二十二）：机械臂逆运动学的数值解方法
机械臂速成小指南（二十三）：Paul方法求解机械臂运动学逆解（含matlab代码）
以下为正文
Paul方法也被称为Paul反变换法，是比较常用的机器人运动学逆解计算方法。该方法要建立机器人的运动学矩阵方程，如式1，等式右边矩阵已知，等式左边矩阵中的关节变量未知。
首先用矩阵
左乘式1矩阵方程，然后从等式两边矩阵元素中寻找并建立含有单关节变量的等式，解出该变量，再寻找并建立其他的单变量等式，如果没能解出所有的关节变量，则再在等式两侧左乘矩阵
，然后再寻找并建立可求解的单变量等式，直到所有的变量都解出。
式1
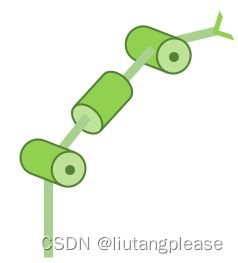
下面，我们以一个三自由度机械臂为例，讲解使用Paul方法得到其逆解。
| i |  |
 |
 |
 |
| 1 | 0 | 0 | 20 | θ1(0) |
| 2 | 0 | -90 | 0 | θ2(0) |
| 3 | 0 | 90 | 12 | θ3(0) |
很显然,该机器人在结构上满足Pieper 准则（6自由度机械臂存在解析解的充分条件是相邻的三个关节旋转轴相交于一点），所以它存在解析解。
由该机器人的DH参数可得各连杆的齐次位姿矩阵为：
假设机器人末端坐标系相对于基坐标系的位姿矩阵为：
则：
即：
式2
采用 Paul反变换法,式2两侧左乘，得：
即：
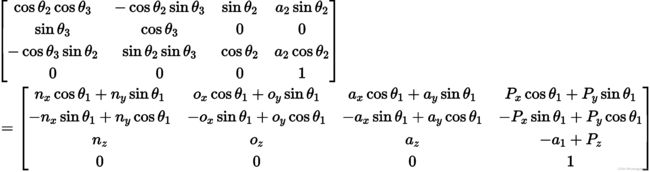式3
由式3等号两侧矩阵（2,3）元素相等，得：
则有两种情况：
| 1 |  |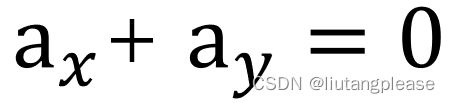
| 2 |  |
对两种情况分别进行讨论及计算（过程省略），最终可得：
第一种情况，当且
时：
其中，
为任意角度。
当且
时：
其中，
为任意角度。
第二种情况，即当时，拥有两组解：
下方Paul反变换法matlab程序包括运动学正解函数、逆解函数和验证程序三部分。
%Forward函数(正解):
function T03 = forward(theta1 ，theta2 ,theta3，a1，a2)
%Eorward函数根据theta值计算末端姿态矩阵,其中thetal,theta2和theta3分别为三个关节角，本程序均以角度进行计算
T01 =[cosd(theta1), - sind(theta1),0,0;
sind(theta1),cosd(theta1),0,0; 0,0,1,al;0,0,0,1];
T12 =[cosd(theta2)，- sind(theta2),0,0;0,0,1,0;-sind(theta2),cosd(theta2),0,0;0,0,0,1];
T23=[cosd(theta3)-sind(theta3),0,0;0,0,-1,- a2; sind(theta3),cosd(theta3),0,0;0,0,0,1];
T03=T01*T12*T23;
%求末端姿态矩阵
%Inverse函数(逆解)
function theta = inverse(T03,a1,a2)
%Inverse函数用于求解逆解中各theta值，参数T03为确定的姿态矩阵
T=T03;
const=45;%theta1的角度值,用户可赋值为任意值,只有当ax=ay=0成立时使用
tol=1e-4;
if (T(1,3)= =0&&T(2,3)= =0) %当ax=ay=0成立时
theta = zeros(1,3);
if abs(T(3,4)-(al + a2))< tolinver_theta2 1=0;
inver_thetal_1= const;
inver_theta3_1= atan2d( - T(1,2),T(1,1))- inver_theta1_1;
theta(1,:) =[inver_thetal_1 ,inver_theta2_1 ,inver_theta3_1];
elseif abs(T(3,4)-(al-a2))< tol
inver_theta2_2=180;
inver_thetal_2= const;
inver_theta3_2= atan2d(T(1,2)，-T(1,1))+ inver_thetal_2;
theta(1,:)=[inver_theta1_2 ,inver_theta2_2，inver_theta3_2] ;
end
else
s2 = (1-T(3,3)^2)^(0.5);
inver theta2_1= atan2d(s2,T(3,3));%theta2 的第一组解
inver theta2_2= atan2d( - s2,T(3,3));%theta2的第二组解
inver_thetal_1 = atan2d(T(2,3),T(1,3));%theta的第一组解
inver_theta1_2=atan2d( -T(2,3)，-T(1,3)) ;theta1 的第二组解
inver_theta3_1 = atan2d(T(3,2) * cscd(inver_theta2_1), -T(3,1) * cscd(inver_theta2_1) ) ;
inver theta3_2 = atan2d(T(3,2) * cscd(inver_theta2_2), -T(3,1) * cscd(inver_theta2_2) ) ;
theta = zeros(2,3);
theta(1,:)=[inver_theta1_1,inver_theta2_1 ,inver_theta3_1];
theta(2,:) = [inver_theta1_2 , inver_theta2_2 , inver_theta3_2];
end
end
%验证程序
clc;
clear all;
close all;
a1_0=12;%取关节长度为12,可任意取值
a2_0=20;%取关节长度为20,可任意取值
T03_0=forward(45,180，-20,a1_0,a2_0);
%调用Eorward函数,求末端姿态矩阵
disp(T03_0);
theta=inverse(T03_0,al_0,a2_0);
%调用 Inverse并输出求得theta解矩阵
disp(theta);
%根据逆解求得的关节角求末端姿态矩阵
[R C]= size(theta);
if R==1 %逆解为无数组解情况时，本例中取inver_theta1_1=45时的特解
T03_verify=zeros(4,4);
T03_verify= forward( theta(1,1),theta(1,2),theta(1,3),a1_0,a2_0);
disp(T03_verify);
elseif R==2%逆解为两组解情况
T03_verify= zeros(4,4,2);
for i=1:2
T03_verify(:,:,i) = forward( theta(i,1), theta(i,2),theta(i,3),a1_0,a2_0);
disp(T03_verify(:,:,i));
end
end