运动员最佳匹配问题【回溯算法】

• Problem Description

羽毛球队有男女运动员各n 人。给定2 个n×n 矩阵P 和Q。P[i][j]是男运动员i 和女运动员j配对组成混合双打的男运动员竞赛优势；Q[i][j]是女运动员i和男运动员j配合的女运动员竞赛优势。由于技术配合和心理状态等各种因素影响，P[i][j]不一定等于Q[j][i]。男运动员i和女运动员j配对组成混合双打的男女双方竞赛优势为P[i][j]*Q[j][i]。
设计一个算法，计算男女运动员最佳配对法，使各组男女双方竞赛优势的总和达到最大。
设计一个算法，对于给定的男女运动员竞赛优势，计算男女运动员最佳配对法，使各组男女双方竞赛优势的总和达到最大。

Input
输入数据的第一行有1 个正整数n (1≤n≤20)。接下来的2n 行，每行n个数。前n行是p，后n行是q。
Output
将计算出的男女双方竞赛优势的总和的最大值输出。

Sample Input

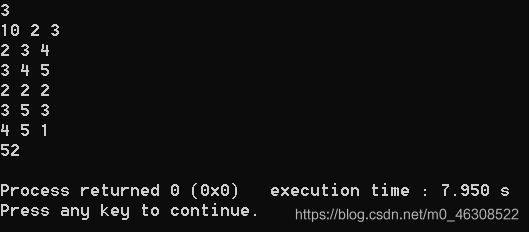
3
10 2 3
2 3 4
3 4 5
2 2 2
3 5 3
4 5 1

Sample Output

52

• 样例分析

对Sample Input给出的数据进行分析，得到了下面的排列树：

注：本题采用的是男运动员选女运动员的方法，这样就构成了一棵排列树。G表示女运动员，排列树的层数表示男运动员。如第一层的G1=20表示，男运动员1号选女运动员1号的男女双方竞赛优势为20。

• 代码实现

#include 
using namespace std;

int n;
int boy[21][21],girl[21][21];   //分别用于存放男、女运动员的竞赛优势
int Max=INT_MIN;   //Max代表男女双方竞赛优势的总和的最大值
int sum=0;   //sum为临时求和
int data[21][21];   //data[i][]用于存放男运动员 i 配对后的双方竞赛优势
int maxSum[21];   //记录每个男生匹配后可达到的最大双方竞赛优势
int book[21];   //用于标记女运动员是否已匹配：book[0]未匹配；book[1]匹配

void dfs(int t)
{
    if(t>=n)   //t到达n之后，代表全部标记访问了,得到了最大值
    {
        Max=max(Max,sum);
        return ;
    }
    int ctn=0;   //剪枝函数：之前t个已匹配好的男女运动员的sum与之后的 t->n-1 个男匹配女的最大值加起来与已经得到的Max比较，若前者<=Max，剪枝
    for(int i=t;i<n;i++)   //求t及t之后男生匹配女生的最大值的和
        ctn+=maxSum[i];
    if(sum+ctn<Max)   //若从第t组->第n组，当前搜索sum加上假设匹配后的最大值cxn，仍然小于Max ，就需要剪枝了，则Max为已经求得的最大值
        return ;
    for(int i=0;i<n;i++)   //若cxn>=Max，要探索子树。从第t个男生开始匹配，找未匹配的女生
    {
        if(!book[i])   //第 i 个女生未匹配
        {
            book[i]=1;   //第 t 个男生匹配女生i
            sum+=data[t][i];   //加上男生t与女生i的男女双方竞赛优势
            dfs(t+1);   //为第i+1个男生匹配
            book[i]=0;   //若第 t 个男生匹配女生i得到的sum不大于Max，则回溯
            sum-=data[t][i];
        }
    }
}

int main()
{
    cin>>n;
    for(int i=0;i<n;i++)   //输入男运动员的竞赛优势
    {
        for(int j=0;j<n;j++)
            cin>>boy[i][j];
    }
    for(int i=0;i<n;i++)   //输入女运动员的竞赛优势
    {
        for(int j=0;j<n;j++)
            cin>>girl[i][j];
    }
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            data[i][j]=boy[i][j]*girl[j][i];   //对每个男生都求男女双方竞赛优势，则能得到i*j种结果（涵盖了P[i][j]*Q[j][i]与Q[i][j]*P[j][i]）
            maxSum[i]=max(maxSum[i],data[i][j]);   //记录每个男生匹配后可达到的最大双方竞赛优势，用于后面的剪枝
        }

    }
    dfs(0);
    cout<<Max<<endl;
    return 0;
}

• 运行结果