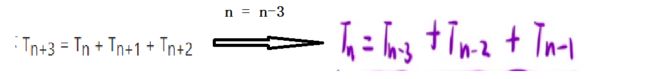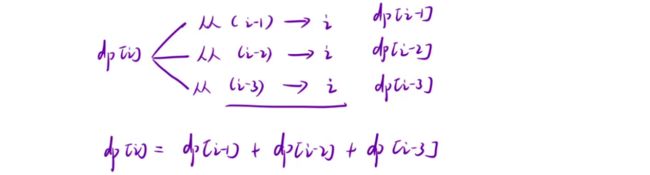【算法】动态规划-斐波那契模型

结论

对于线性dp，一般是用经验+题目要求来定义状态表示：

• 以某个位置为结尾…
• 以某个位置为起点…。

斐波那契模型

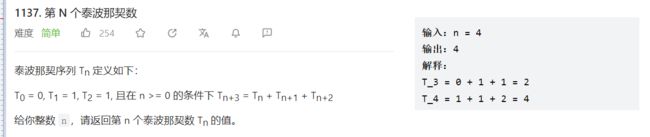
第 N 个泰波那契数

https://leetcode.cn/problems/n-th-tribonacci-number/

分析

1.状态表示：

• dp[i]:表示第i个泰波那契数的值

2.状态转移方程分析：

• 

• 所以状态转移方程为：dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]

3.初始化< ==>目的是为了防止填dp表的时候不越界

• 当前位置的值依赖的是前面3个位置的值，所以需要初始化dp[0]，dp[1]，dp[2]，题目已经给出T0，T1，T2的值

4.填表顺序

• 从第三个位置开始，从左往右填表

5.返回值

• 求的是第 n 个泰波那契数的值，所以返回:dp[n]

class Solution {
public:
    int tribonacci(int n) {
        if(n == 0 || n == 1) return n;
        if(n == 2) return 1;
        vector<int> dp(n+1);
        dp[0] = 0,dp[1]=1,dp[2] = 1;
        for(int i = 3;i<=n;i++)
        {
            dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
        }
        return dp[n];
    }
};

---

优化：使用滚动数组优化

class Solution {
public:
    int tribonacci(int n) {
        if(n == 0 || n == 1) return n;
        if(n == 2) return 1;
        //a:dp[i-3] b:dp[i-2] c:dp[i-1]
        int a  = 0,b = 1,c = 1,d = 0;
        for(int i = 3;i<=n;i++)
        {
            d = a + b + c;
            //a b c三者赋值
            a = b;
            b = c;
            c = d;
        }
        return d;
    }
};

---

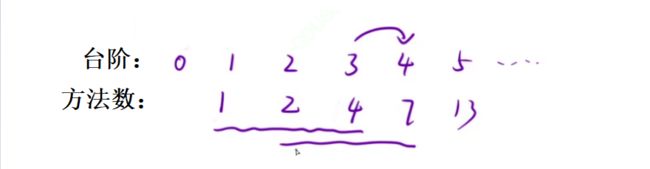
三步问题

https://leetcode.cn/problems/three-steps-problem-lcci/

分析

1.状态表示

• dp[i]：到达i位置的时候，一共有多少种方法

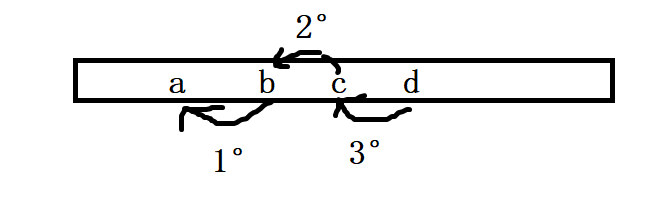
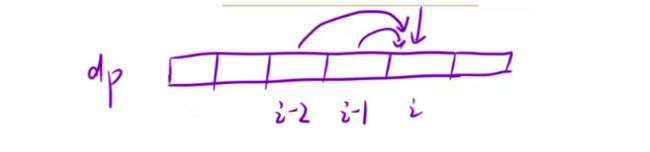
2.状态转移方程 ： 以$i$位置状态的最近的⼀步，来分情况讨论：

• 可以从三个位置来到当前位置
  • 1.从i-1位置跳1阶台阶来到当前位置 此时的方法数为dp[i-1]
  • 2.从i-2位置跳2阶台阶来到当前位置 此时的方法数为dp[i-2]
  • 3.从i-3位置跳3阶台阶来到当前位置 此时的方法数为dp[i-3]

**注意：**由于结果可能很⼤，需要对结果取模。

对于这类需要取模的问题，我们每计算⼀次（两个数相加/乘等），都需要取⼀次模，否则可能发⽣了溢出

//err写法: (dp[i - 1] + dp[i - 2] + dp[i - 3])  % MOD
//正确写法   
dp[i] = ((dp[i - 1] + dp[i - 2]) % MOD + dp[i - 3]) % MOD;

3.初始化 ==>为了填表的时候不越界

• 因为当前位置依赖的是前3个位置，所以要将dp[1] = 1，dp[2] = 2，dp[3] = 4初始化，从第四个位置开始填表
• 这里的dp[0]位置不需要处理，当然也可以处理dp[0] = 0

4.填表顺序

• 从左往右填表

5.返回值

• 返回dp[n] ：到达n位置(n层台阶)的时候的方法数

class Solution {
public:
    const int MOD = 1e9+7;
    int waysToStep(int n) {
        if(n == 1 || n == 2) return n;
        if(n == 3) return 4;
        vector<int> dp(n+1);
        dp[1] = 1,dp[2] = 2,dp[3] = 4;
        for(int i = 4;i<=n;i++)
        {
            dp[i] = (((dp[i-1]+dp[i-2]) % MOD ) + dp[i-3]) % MOD;
        }
        return  dp[n];
    }
};

---

使用最小花费爬楼梯

https://leetcode.cn/problems/min-cost-climbing-stairs/

注意坑点：此处的[0，n-1]位置代表的都是楼层，n位置代表的才是楼顶！！！

分析

**方法1：**以i位置为结尾…

1.状态表示

• dp[i]：到达i位置的时候的最小花费

2.状态转移方程：根据最近的⼀步，分情况讨论

• 由于支付i位置的费用之后，可以往后走1步/2步

• case1：先到达i-1位置，然后支付i-1位置的花费cost[i-1]，从i-1位置往后走1步来到i位置
  • 此时的花费为：到达i-1位置时候的最小花费 +支付i-1位置的花费 dp[i-1] + cost[i-1]
• case2：先到达i-2位置，然后支付i-2位置的花费cost[i-2]，从i-2位置往后走2步来到i位置
  • 此时的花费为：到达i-2位置时候的最小花费 +支付i-2位置的花费 dp[i-2] + cost[i-2]
• 此时dp[i]的值为case1和case2的较小值 dp[i] = min(dp[i-1] + cost[i-1],dp[i-2]+cost[i-2])

3.初始化

• 当前i位置依赖前两个位置的值，需要初始化第0个和第1个位置，防止填表的时候越界
• 题目已经说明：可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯，所以dp[0] = dp[1] = 0

4.填表顺序

• 从左往右，从第2个位置往后填表

5.返回值

• 返回dp[n]：到达n位置(楼顶)的时候的最小花费

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        //楼梯顶部：n位置
        //dp[i]:到达i位置时的最小花费
        int n = cost.size();
        vector<int> dp(n+1);
        //可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯 ==> 0和1位置不需要花费
        dp[0] = dp[1] = 0;
        //到达i位置时的最小花费 = min(到达i-1位置时的最小花费 + 花i-1位置的钱跳1步,到达i-2位置时的最小花费 + 花i-2位置的钱跳2步)
        for(int i = 2;i<=n;i++)
            dp[i] = min(dp[i-1] + cost[i-1],dp[i-2] + cost[i-2]);
        return dp[n];
    }
};

---

方法2：以i位置为起点…

1.状态表示

• dp[i]：以i位置为起点，到达楼顶的时候的最小花费

2.状态转移方程：根据最近的⼀步，分情况讨论：

• case1：支付i位置的花费之后，往后走一步，从i+1位置为起点到达楼顶， 此时花费为：cost[i] + dp[i+1]
• case2：支付i位置的花费之后，往后走一步，从i+2位置为起点到达楼顶 ，此时花费为：cost[i] + dp[i+2]
• 由于要的是最小花费，所以: dp[i] = min(dp[i + 1], dp[i + 2]) + cost[i]

3.初始化

• 为了保证填表的时候不越界，需要初始化最后两个位置的值，n-1位置到达楼顶的最小花费就是花费当前i-1位置的值，然后往后走1步，n-2位置同理
• dp[n-1] = cost[n-1] dp[n-2] = cost[n-2]

4.填表顺序

• 当前i位置依赖的是后面的两个位置，所以从n-3位置，右往左遍历

5.返回值

• 因为最初可以站在0位置/1位置，所以应该返回dp[0]和dp[1]的较小值

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int n = cost.size();
        //dp[i]:以i位置为起点,到达楼顶的最小花费
        //case1:花费i位置的钱，往后走1步到达i+1位置，然后再到达楼顶
        //case2:花费i位置的钱，往后走2步到达i+2位置，然后再到达楼顶
        //dp[i] = min(dp[i+1],dp[i+2]) + cost[i]
        vector<int> dp(n);
        dp[n-1] = cost[n-1],dp[n-2] = cost[n-2];
        for(int i = n - 3;i>=0;i--)
            dp[i] = min(dp[i+1],dp[i+2]) + cost[i];
        //可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯，选择最小花费
        return min(dp[0],dp[1]);
    }
};

---

解码方法

https://leetcode.cn/problems/decode-ways/

分析

1.状态表示

• dp[i]:以i位置为结尾时，解码的方法数 (字符串$[0，i]$区间上的字符，有多少种解码方法)

2.状态转移方程 ==>根据最近的一步划分问题

• case1：i位置的数单独解码成一个字母

  • 解码成功：i位置的字符在$[1,9]$之间才可以单独解码，此时以i位置结尾时解码的方法数 等于 以i-1位置结尾时解码的方法数，就是：$[0，i-1]$区间上的所有解码结果，后面跟上i位置解码后的字⺟
  • 解码失败：当$i$位置上的数0的时候，此时i位置上的数是不能单独解码的，此时$$[0，i]$$区间上不存在解码结果，此时前⾯做的努⼒就全部⽩费了，dp[i] = 0

• case2：i位置和i-1位置的数结合，共同解码成一个字母

  • 解码成功：当结合的数在$[10, 26] $之间的时候，说明i-1位置和i位置的字符可以共同解码，此时以i位置结尾时解码的方法数\ast \ast 等于\ast \ast 以i-2位置结尾时解码的方法数，也就是：$[0，i-2]$区间上的所有解码结果，后面跟i和i-1位置的共同解码后的字母
  • 解码失败：当结合的数在$[0, 9] $ || $[27,99]$的时候，说明$i$和$i-1$位置结合后解码失败，要注意有前导0的情况！！！如：00，01… ，此时$$[0，i]$$区间上不存在解码结果，此时前⾯做的努⼒就全部⽩费了，dp[i] = 0

假设i位置的字符为a，i-1位置的字符为b

总结：

• 当$s[i]$ 上的数在 $[1, 9] $区间上时： dp[i] += dp[i - 1] ；
• 当$ s[i - 1] $ 与$ s[i] $ 上的数结合后，在$ [10, 26] $ 之间的时候： dp[i] +=dp[i - 2]
• 若上述两个判断都不成⽴，说明没有解码⽅法，dp[i] = 0

3.初始化

• 需要初始化dp表0位置和1位置的值

• 对于dp[0]： 如果0位置的字符是${}^{\prime }{0}^{\prime }$ ，此时没有解码方法，dp[0] = 0。 如果不是字符0，那么可以解码成功，dp[0] = 1

• 对于dp[1]：

  • 如果1位置的字符在$[1,9]$之间，那么能单独解码，此时dp[1] = 1 ，否则dp[1] = 0。 错误！！！ 必须要0位置和1位置都能单独解码，此时才算1种解码方法，例如: 06，此时1位置是能单独解码的，但是由于0位置不能单独解码！所以1位置单独解码是失败的

  • 如果0位置和1位置的字符结合后的数在$[10，26]$之间，说明前两个字符可以构成一种解码方法 dp[1] += 1

4.填表顺序

• 从第二个位置开始，左往右填表

5.返回值

• 返回dp[n-1]：以n-1位置为结尾时，解码的方法数

class Solution {
public:
    int numDecodings(string s) {
        int n = s.size();
        //dp[i]:以i位置为结尾(字符串[0,i]区间上的字符)，有多少种解码方法数
        //case1:i位置单独解码 若成功:dp[i] += dp[i-1]
        //case2:i和i-1位置共同解码，若成功:dp[i] += dp[i-2]
        vector<int> dp(n);
        dp[0] = s[0] != '0'; //如果0位置是字符0，那么0位置就不能单独
        if(n == 1) return dp[0];

        //0位置和1位置都能单独解码，此时才算1种解码方法
        dp[1] = s[1] != '0' && s[0] != '0'; 
        int sum = (s[0] - '0') * 10 + (s[1] - '0');//0位置和1位置共同解码形成的值,如果范围在[10,26],才可以一起解码
        if(sum >= 10 && sum <= 26) dp[1] += 1;//此时0位置和1位置可以一起解码

        for(int i = 2;i<n;i++)
        {
            //i位置:单独解码 or 和i-1位置一起解码

            //case1:i位置单独解码，此时以i位置为结尾的解码方法数就是i-1位置结尾的解码方法数(也就是：[0,i-1]区间上的所有解码结果，后面跟上i位置解码后的字⺟)
            if(s[i] != '0') dp[i] += dp[i-1];
            //case2:i和i-1位置共同解码
            int sum = (s[i-1] - '0') * 10 + (s[i] - '0');
            //此时i位置和i-1位置可以一起解码，此时以i位置为结尾的解码方法数就是i-2位置结尾的解码方法数(也就是：[0,i-2]区间上的所有解码结果，后面跟上i和i-1位置解码后的字⺟)
            if(sum >= 10 && sum <= 26)
                dp[i] += dp[i-2];
        }
        return dp[n-1];
    }
};

---