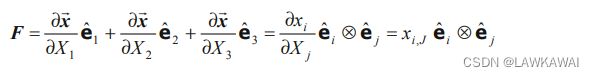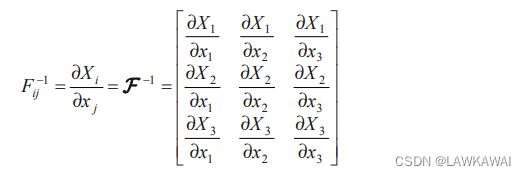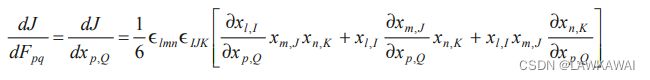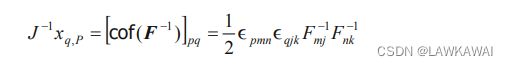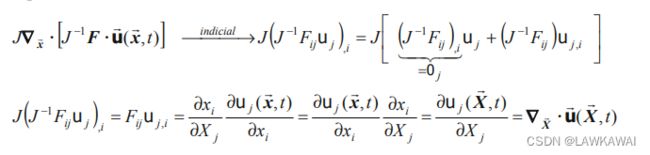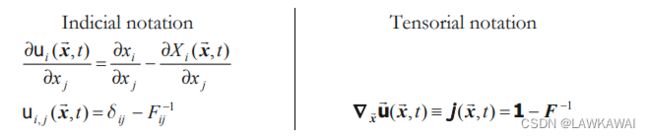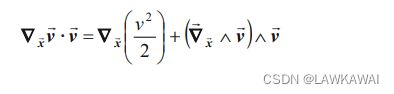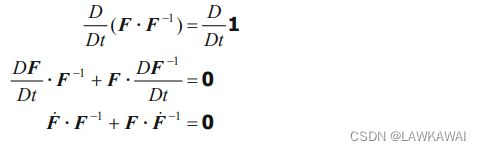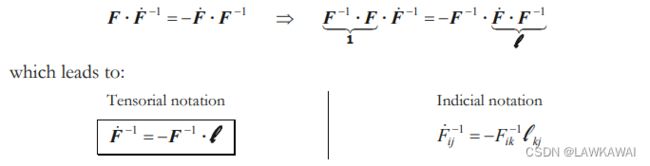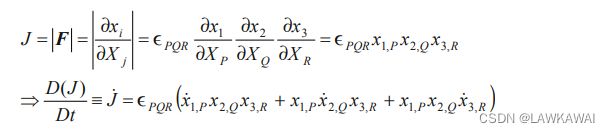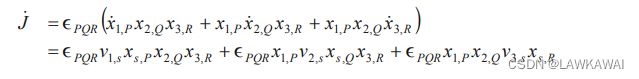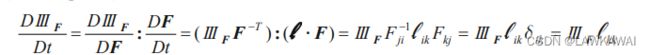【连续介质力学】变形梯度
变形梯度
简介
本节讨论两个不同质点P和Q的之间的相对运动变化
拉伸比和相对伸长
d X ⃗ d\vec X dX : 在参考构形连接质点P和Q的向量,线单元
M ^ \hat M M^: d X ⃗ d\vec X dX方向的单位向量
d x ⃗ d\vec x dx : 在当前构形连接质点P’和Q‘的向量,线单元
m ^ \hat m m^: d x ⃗ d\vec x dx方向的单位向量
d S dS dS: d X ⃗ d\vec X dX的大小, d S = ∣ ∣ d X ⃗ ∣ ∣ = ∣ ∣ P Q ⃗ ∣ ∣ dS = ||d \vec X||=||\vec {PQ}|| dS=∣∣dX∣∣=∣∣PQ∣∣
d s ds ds: d x ⃗ d\vec x dx的大小, d s = ∣ ∣ d x ⃗ ∣ ∣ = ∣ ∣ P ′ Q ′ ⃗ ∣ ∣ ds = ||d \vec x||=||\vec {P'Q'}|| ds=∣∣dx∣∣=∣∣P′Q′∣∣
- 拉伸比 λ m ^ \lambda_{\hat m} λm^ , 沿着 m ^ \hat m m^方向:

范围: 0 < λ m ^ < ∞ 0 < \lambda_{\hat m} < \infty 0<λm^<∞ , 当 d s → 0 , λ m ^ → 0 当 ds \to 0, \lambda_{\hat m}\to 0 当ds→0,λm^→0
当 d s → 0 , λ m ^ → 0 当 ds \to 0, \lambda_{\hat m}\to 0 当ds→0,λm^→0
当 d s → ∞ , λ m ^ → ∞ 当 ds \to \infty, \lambda_{\hat m}\to \infty 当ds→∞,λm^→∞
不可穿透原理: d s ≠ 0 ⟹ λ m ^ ≠ 0 ds \neq 0 \implies \lambda_{\hat m} \neq 0 ds=0⟹λm^=0
如果不是的话,那么将会同时有两个质点占据着相同的位置
λ m ^ = 1 \lambda_{\hat m}=1 λm^=1: 没有伸长
0 < λ m ^ < 1 0<\lambda_{\hat m}<1 0<λm^<1: P Q ⃗ \vec {PQ} PQ 缩短
λ m ^ > 1 \lambda_{\hat m} > 1 λm^>1: 两个质点之间距离变大
范围: − 1 < ϵ m ^ < ∞ -1 < \epsilon_{\hat m} < \infty −1<ϵm^<∞
物质和空间的变形梯度
运动的质点描述: x ⃗ = x ⃗ ( X ⃗ , t ) \vec x = \vec x(\vec X, t) x=x(X,t)

如果将 x ⃗ Q ( X ⃗ Q , t ) \vec x^Q(\vec X^Q, t) xQ(XQ,t)表示成:
![]()
那么,当前构形的向量场 d x ⃗ d \vec x dx表示为:

由于P和Q离得足够近,所以高阶项可以去掉:
d x ⃗ = ∂ x i ∂ X k d X k e ^ i = F i k d X k e ^ i d\vec x=\frac{\partial x_i}{\partial X_k}dX_k\hat e_i=F_{ik}dX_k\hat e_i dx=∂Xk∂xidXke^i=FikdXke^i
or:
d x ⃗ = F ⋅ d X ⃗ \boxed{d\vec x=F\cdot d\vec X} dx=F⋅dX
其中 F F F 是二阶张量,被称为物质变形梯度
是从 d X ⃗ d\vec X dX(未变形构形)到 d x ⃗ d\vec x dx(变形构形)的一个线性变换
也可以从梯度的定义出发得到:
标量场: ϕ = ϕ ( x ⃗ , t ) \phi = \phi(\vec x, t) ϕ=ϕ(x,t)
全微分: d ϕ ( x ⃗ , t ) = ∇ ϕ ⋅ d x ⃗ = ∂ ϕ ( x ⃗ , t ) ∂ x ⃗ ⋅ d x ⃗ d\phi(\vec x, t)=\nabla\phi\cdot d\vec x= \frac{\partial \phi(\vec x, t)}{\partial \vec x}\cdot d\vec x dϕ(x,t)=∇ϕ⋅dx=∂x∂ϕ(x,t)⋅dx
若 x ⃗ ( X ⃗ , t ) \vec x(\vec X, t) x(X,t), 则:
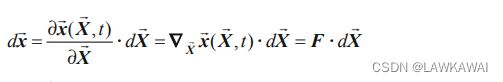
直角坐标系下的 d x ⃗ d\vec x dx的分量可以通过以下点乘得到:

可以用下标大写表示:
∗ i , J ≡ ∂ ∗ i ∂ X j ≠ ∗ i , j ≡ ∂ ∗ i ∂ x j *_{i,J}\equiv\frac{\partial *_i}{\partial X_j} \neq *_{i,j} \equiv \frac{\partial *_i}{\partial x_j} ∗i,J≡∂Xj∂∗i=∗i,j≡∂xj∂∗i
用大写Grad表示:
G r a d ( ∗ ) = ∇ X ⃗ ( ∗ ) = ∂ ( ∗ ) ∂ X i ⨂ e ^ i Grad(*)=\nabla_{\vec X}(*)=\frac{\partial (*)}{\partial X_i} \bigotimes \hat e_i Grad(∗)=∇X(∗)=∂Xi∂(∗)⨂e^i
g r a d ( ∗ ) = ∇ x ⃗ ( ∗ ) = ∂ ( ∗ ) ∂ x i ⨂ e ^ i grad(*)=\nabla_{\vec x}(*)=\frac{\partial (*)}{\partial x_i} \bigotimes \hat e_i grad(∗)=∇x(∗)=∂xi∂(∗)⨂e^i
方程的逆变换:
d X ⃗ = F − 1 ⋅ d x ⃗ \boxed{d \vec X = F^{-1} \cdot d \vec x} dX=F−1⋅dx
其中 F − 1 F^{-1} F−1 是空间变形梯度

根据代数余子式和逆矩阵的定义:

用张量的第三主不变量表示上述方程:

方程的逆:
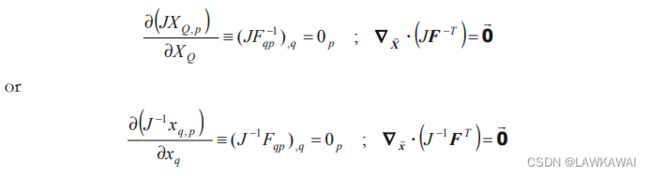
证明如下:

在kq , 张量 ϵ q j k = ϵ j k q = − ϵ j q k \epsilon_{qjk}=\epsilon_{jkq}=-\epsilon_{jqk} ϵqjk=ϵjkq=−ϵjqk 是反对称的,然而 x n , k q x_{n, kq} xn,kq是对称的, 所以 ϵ q j k x n , k q = 0 j n \epsilon_{qjk}x_{n,kq}=0_{jn} ϵqjkxn,kq=0jn
所以可以证明 ( J − 1 x q , p ) , q = 0 (J^{-1}x_{q,p})_{,q}=0 (J−1xq,p),q=0
如果 u ⃗ ( x ⃗ , t ) \vec u(\vec x, t) u(x,t) 和 σ ( x ⃗ , t ) \sigma (\vec x, t) σ(x,t) 分别是向量和二阶张量,满足以下关系:
问题2.5 ϕ ( X ⃗ , t ) \phi(\vec X, t) ϕ(X,t) 是一个拉格朗日描述的标量场
位移梯度张量(物质和空间描述)
位移 u ⃗ \vec u u 的拉格朗日和欧拉描述:

对位移 u i ( X ⃗ , t ) = x i ( X ⃗ , t ) − X i u_i(\vec X, t)=x_i(\vec X, t)-X_i ui(X,t)=xi(X,t)−Xi 关于 X ⃗ \vec X X 求偏导:
对位移 u i ( x ⃗ , t ) = x i − X i ( x ⃗ , t ) u_i(\vec x, t)=x_i - X_i(\vec x, t) ui(x,t)=xi−Xi(x,t) 关于 X ⃗ \vec X X 求偏导:
j \mathcal j j 是空间位移梯度张量
由于:
可以得到 j 和 J \mathcal j 和 \mathcal J j和J之间的关系:
问题2.6 位移场
变形梯度的物质时间导数和雅可比行列式的物质时间导数
F F F 的物质时间导数——空间速度梯度
F F F 的物质时间导数:

将速度表示成欧拉形式, v i ( X ⃗ ( x ⃗ , t ) , t ) v_i(\vec X(\vec x, t), t) vi(X(x,t),t) , 应用链式法则:
F ˙ = l ⋅ F \boxed{\dot F = \mathcal l \cdot F} F˙=l⋅F
其中 l \mathcal l l 是空间速度梯度,定义为:
l ( x ⃗ , t ) = ∇ x ⃗ v ⃗ ( x ⃗ , t ) = F ˙ ⋅ F − 1 空间速度梯度 \boxed{\mathcal l(\vec x, t)=\nabla_{\vec x}\vec v(\vec x, t)=\dot F \cdot F^{-1}} 空间速度梯度 l(x,t)=∇xv(x,t)=F˙⋅F−1空间速度梯度
问题2.7 令 d x ⃗ d\vec x dx 是一个在当前构形下的微分线单元, 求 d x ⃗ d\vec x dx 的物质时间导数

D D t d x ⃗ = ∇ x ⃗ v ⃗ ⋅ d x ⃗ \frac{D}{Dt}d\vec x=\nabla_{\vec x}\vec v\cdot d \vec x DtDdx=∇xv⋅dx
变形率和自旋张量
张量 l \mathcal l l 可以分解成对称部分和反对称部分:
l s y m = D ( x ⃗ , t ) \mathcal l^{sym}=D(\vec x, t) lsym=D(x,t)- 变形率张量
l s k e w = W ( x ⃗ , t ) \mathcal l^{skew}=W(\vec x, t) lskew=W(x,t)-自旋、旋转率张量或涡量张量
D D D 和 W W W 的分量分别是:
可以定义涡度向量场 ω ⃗ = 2 w ⃗ \vec \omega=2 \vec w ω=2w
另外,根据反对称张量定义:
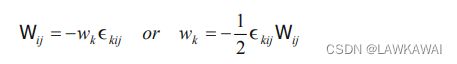
并且已经证明过 : 2 w ⃗ = r o t ( v ⃗ ) = ∇ ⃗ x ⃗ ∧ v ⃗ 2 \vec w=rot(\vec v)= \vec \nabla_{\vec x} \wedge \vec v 2w=rot(v)=∇x∧v
其中 w ⃗ \vec w w 是反对称张量 ( ∇ x ⃗ v ⃗ ) s k e w (\nabla_{\vec x}\vec v)^{skew} (∇xv)skew 关联的轴向量, 因此涡度向量表示为:
ω ⃗ = 2 w ⃗ = r o t ( v ⃗ ) = ∇ ⃗ x ⃗ ∧ v ⃗ 涡度向量 \boxed{\vec \omega=2\vec w = rot(\vec v)=\vec \nabla_{\vec x}\wedge \vec v} 涡度向量 ω=2w=rot(v)=∇x∧v涡度向量
由于下式成立:
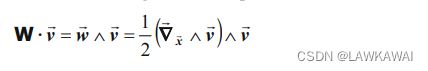
那么 D = 0 D = 0 D=0 表征为一个刚体运动,此外, D ( d x ⃗ ) D t = w ⃗ ∧ d x ⃗ \frac{D(d\vec x)}{Dt}=\vec w \wedge d \vec x DtD(dx)=w∧dx成立,以下为证明:

为了证明 D = 0 D = 0 D=0 表征的是刚体运动,也就是说质点之间的距离是不发生改变的,也就是说 d x ⃗ d\vec x dx的大小不随时间改变, 所以考察一下 ∣ ∣ d x ⃗ ∣ ∣ 2 ||d \vec x||^2 ∣∣dx∣∣2 的物质时间导数:
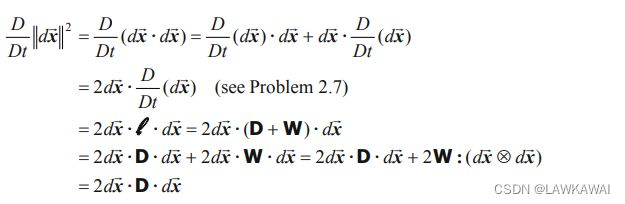
其中,用到了 A s k e w : B s y m = 0 ⟹ W : ( d x ⃗ ⨂ d x ⃗ ) = 0 A^{skew}:B^{sym}=0 \implies W:(d \vec x \bigotimes d \vec x)=0 Askew:Bsym=0⟹W:(dx⨂dx)=0,所以 d x ⃗ d \vec x dx 的大小不随时间改变
如果自旋张量是一个零张量 W = 0 W = 0 W=0, 那么速度场被认为是无旋的, 因此 ∇ ⃗ x ⃗ ∧ v ⃗ = 0 ⃗ \vec \nabla_{\vec x} \wedge \vec v=\vec 0 ∇x∧v=0
在问题2.3 中,以下的关系是成立的:
∇ x ⃗ v ⃗ ⋅ v ⃗ = ∇ x ⃗ ( v 2 2 ) + 1 2 ( ∇ ⃗ x ⃗ ∧ v ⃗ ) ∧ v ⃗ \nabla _{\vec x}\vec v \cdot \vec v=\nabla_{\vec x}(\frac{v^2}{2})+\frac{1}{2}(\vec \nabla_{\vec x}\wedge \vec v) \wedge \vec v ∇xv⋅v=∇x(2v2)+21(∇x∧v)∧v
推导:

2 ( ∇ x ⃗ v ⃗ ) T ⋅ v ⃗ 2 (\nabla_{\vec x} \vec v)^T\cdot \vec v 2(∇xv)T⋅v 可以写成下标形式 2 v j , i v j 2 v_{j,i} v_j 2vj,ivj, 等价于
( ∣ ∣ v ⃗ ∣ ∣ 2 ) , i = ( v 2 ) , i = ( v ⃗ ⋅ v ⃗ ) , i = ( v j v j ) , i = v j , i v j + v j v j , i = 2 v j v j , i (||\vec v||^2)_{,i}=(v^2)_{,i}=(\vec v \cdot \vec v)_{,i}=(v_jv_j)_{,i}=v_{j,i}v_j+v_jv_{j,i}=2v_jv_{j,i} (∣∣v∣∣2),i=(v2),i=(v⋅v),i=(vjvj),i=vj,ivj+vjvj,i=2vjvj,i
因此:
F − 1 F^{-1} F−1 的物质时间导数
空间变形梯度 F − 1 F^{-1} F−1 的物质时间导数:
F ˙ − 1 = − F − 1 ⋅ l \boxed{\dot F^{-1}=-F^{-1}\cdot \mathcal l} F˙−1=−F−1⋅l
雅可比行列式的物质时间导数
雅可比行列式的物质时间导数:
以下关系成立:

将以上 x ˙ 1 , P , x ˙ 2 , Q , x ˙ 3 , R \dot x_{1,P}, \dot x_{2,Q}, \dot x_{3,R} x˙1,P,x˙2,Q,x˙3,R 代入到 D ( J ) D t \frac{D(J)}{Dt} DtD(J):
第一项表示为:
T r ( l ) = T r ( D + W ) = T r ( D ) + T r ( W ) = T r ( D ) Tr(\mathcal l)=Tr(D + W)=Tr(D) + Tr(W) =Tr(D) Tr(l)=Tr(D+W)=Tr(D)+Tr(W)=Tr(D)
雅可比行列式的物质时间导数也可以表示成:
问题 2.8
参考教材:
Eduardo W.V. Chaves, Notes On Continuum Mechanics