吴恩达471机器学习入门课程1第3周——逻辑回归

Logistic Regression

实施逻辑回归并将其应用于两个不同的数据集。

1、导包

import numpy as np
import matplotlib.pyplot as plt
from utils import *
import copy
import math
from mpl_toolkits.mplot3d import Axes3D

2、逻辑回归

在这一部分中,你将建立一个逻辑回归模型来预测学生是否被大学录取。

2.1、问题描述

假设你是一所大学部门的管理员，并且想要根据每个申请人在两次考试中的成绩来确定他们被录取的机会。

• 你有先前申请者的历史数据，可以将其用作逻辑回归的训练集。
• 对于每个训练实例，你都有申请者在两次考试中的分数和录取决定。
• 你的任务是构建一个分类模型，根据这两次考试的成绩估计申请人被录取的概率。

2.2、加载数据集

x_train,y_train = load_data('data/ex2data1.txt')

y_train[:5]

array([0., 0., 0., 1., 1.])

数据可视化

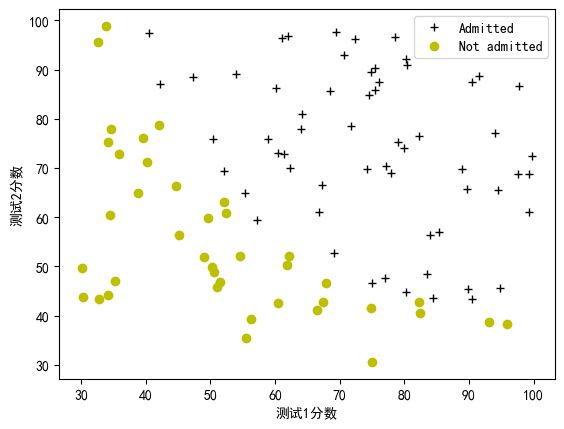
在实现任何学习算法之前，如果可能的话最好先可视化数据。下面的代码将数据显示在一个二维图中（如下所示），其中两个考试分数是轴，正负样本用不同的标记表示。

plot_data(x_train,y_train,pos_label="Admitted",neg_label="Not admitted")
plt.rcParams['font.sans-serif']=['SimHei']
plt.ylabel("测试2分数")
plt.xlabel("测试1分数")
plt.legend(loc="upper right")
plt.show()

2.3、sigmod function

回顾一下逻辑回归，该模型表示为

$$f_{\mathbf{w},b}(x)=g(\mathbf{w}\cdot \mathbf{x}+b)$$
其中函数 $g$ 是Sigmoid函数。Sigmoid函数定义如下：

$$g(z)=\frac{1}{1+e^{-z}}$$

现在，我们先实现Sigmoid函数，以便在接下来的任务中使用。

注意：

• 参数 z 不一定是单个数字，也可能是数组。
• 如果参数是数组，则需要将Sigmoid函数应用于数组中的每个元素。

def sigmod(z):
    return 1/(1+np.exp(-z))

2.4 逻辑回归的代价函数

在这个部分，你将会实现逻辑回归的代价函数。

请你使用下面的公式来完成 compute_cost 函数。

回想一下，在逻辑回归中，代价函数的形式为

$$J(\mathbf{w},b)=\frac{1}{m}\sum _{i=0}^{m-1}\left[loss(f_{\mathbf{w},b}({\mathbf{x}}^{(i)}),y^{(i)})\right]\text{\hspace{1em}(1)}$$

其中

• m 是数据集中训练样本数目

• $loss(f_{\mathbf{w},b}({\mathbf{x}}^{(i)}),y^{(i)})$ 是单个数据点的代价，它的表达式为 -

  $$loss(f_{\mathbf{w},b}({\mathbf{x}}^{(i)}),y^{(i)})=(-y^{(i)}\log \left(f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)-\left(1-y^{(i)}\right)\log \left(1-f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)\text{\hspace{1em}(2)}$$

• $f_{\mathbf{w},b}({\mathbf{x}}^{(i)})$ 是模型的预测值，而 $y^{(i)}$ 则是实际的标签。

• $f_{\mathbf{w},b}({\mathbf{x}}^{(i)})=g(\mathbf{w}\cdot {\mathbf{x}}^{(\mathbf{i})}+b)$ ，其中 $g$ 是 sigmoid 函数。

  • 首先计算一个中间变量 $z_{\mathbf{w},b}({\mathbf{x}}^{(i)})=\mathbf{w}\cdot {\mathbf{x}}^{(\mathbf{i})}+b=w_0{x}_0^{(i)}+...+w_{n-1}{x}_{n-1}^{(i)}+b$ ，其中 $n$ 是特征数量，然后再计算 $f_{\mathbf{w},b}({\mathbf{x}}^{(i)})=g(z_{\mathbf{w},b}({\mathbf{x}}^{(i)}))$

注意：

• 在完成这个部分的代码时，请记住变量 X_train 和 y_train 不是标量值，它们是形状分别为 ($m,n$) 和 (m,1) 的矩阵，其中n是特征数量，m 是训练样本数目。
• 可以使用之前实现的 sigmoid 函数来帮助你完成这个部分的代码。

def compute_cost(x,y,w,b):
    m,n = x.shape
    cost = 0
    for i in range(m):
        z = np.dot(x[i],w)+b
        f_wb = sigmod(z)
        cost += -y[i]*np.log(f_wb)-(1-y[i])*np.log(1-f_wb)
    return cost/m

2.5 逻辑回归的梯度

在这一节中，您将实现逻辑回归的梯度。

回忆一下，梯度下降算法是：

$$\begin{array}{rlrlrl}& \text{重复直到收敛:}\{& b:=b-\alpha \frac{\partial J(\mathbf{w},b)}{\partial b}& w_j:=w_j-\alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j}& \text{for j := 0..n-1}& \}\end{array}\text{\hspace{1em}(1)}$$

这里参数 $b$，$w_j$ 都被同时更新了。

请完成 compute_gradient 函数，从以下公式（2）和（3）中计算 $\frac{\partial J(\mathbf{w},b)}{\partial w}$，$\frac{\partial J(\mathbf{w},b)}{\partial b}$。

$$\frac{\partial J(\mathbf{w},b)}{\partial b}=\frac{1}{m}\sum _{i=0}^{m-1}(f_{\mathbf{w},b}({\mathbf{x}}^{(i)})-{\mathbf{y}}^{(i)})\text{\hspace{1em}(2)}$$
$$\frac{\partial J(\mathbf{w},b)}{\partial w_j}=\frac{1}{m}\sum _{i=0}^{m-1}(f_{\mathbf{w},b}({\mathbf{x}}^{(i)})-{\mathbf{y}}^{(i)})x_j^{(i)}\text{\hspace{1em}(3)}$$

• m 是数据集中训练样例的数量

• $f_{\mathbf{w},b}(x^{(i)})$ 是模型的预测值，$y^{(i)}$ 是实际标签

• 注意: 虽然该梯度看起来与线性回归梯度相同，但实际上公式是不同的，因为线性和逻辑回归对 $f_{\mathbf{w},b}(x)$ 有不同的定义。

与以前一样，您可以使用上面实现的 sigmoid 函数，如果遇到困难，可以查看下面的提示，以帮助您完成实现。

def compute_gradient(x,y,w,b):
    m,n = x.shape
    dj_dw = np.zeros(w.shape)
    dj_db = 0.
    for i in range(m):
        f_wb_i = sigmod(np.dot(x[i],w)+b)
        cost_i = f_wb_i - y[i]
        for j in range(n):
            dj_dw[j] += cost_i*x[i,j]
        dj_db += cost_i
    return dj_dw/m,dj_db/m

2.6 使用梯度下降学习参数

与之前的任务类似，现在您将使用梯度下降法找到逻辑回归模型的最佳参数。

• 在这个部分，您无需实现任何内容，只需要运行以下单元格即可。

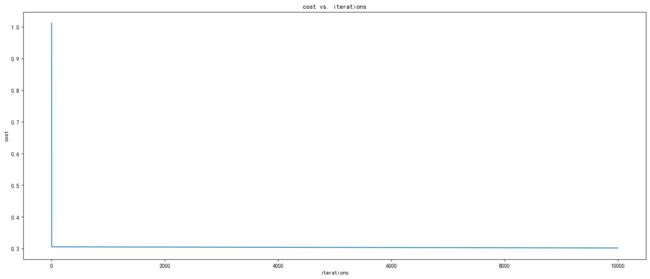
• 一个验证梯度下降是否正确工作的好方法是观察$J(\mathbf{w},b)$的值，并检查它是否随着每次迭代而减小。

• 假设您已经实现了梯度并计算成本函数的值，在算法结束时，$J(\mathbf{w},b)$的值应该会收敛到一个稳定值，并且永远不会增加。

def gradient_descent(x,y,w_in,b_in,cost_function,gradient,alpha,num_iters):
    w = copy.deepcopy(w_in)
    b = b_in
    J_history = []
    w_history = []
    for i in range(num_iters):
        dj_dw,dj_db = gradient(x,y,w,b)
        w -= alpha* dj_dw
        b -= alpha* dj_db
        cost = cost_function(x,y,w,b)
        J_history.append(cost)
        w_history.append([wi.copy() for wi in w])
    return w,b,J_history,w_history

测试

np.random.seed(123)
"""
np.random.rand(2)是生成两个0到1之间的随机数，然后减去0.5得到的结果是在[-0.5, 0.5]之间，
最后乘以0.01得到的结果就是在[-0.005, 0.005]之间的随机数。reshape(-1,1)将生成的一维数组转换成两行一列的矩阵形式，作为intial_w的值。
"""
init_w = 0.01 * (np.random.rand(2).reshape(-1,1) - 0.5)
init_b = -8
iterations = 10000
alpha = 0.001
w,b, J_history,w_history = gradient_descent(x_train ,y_train, init_w, init_b,compute_cost, compute_gradient, alpha, iterations)

cost = np.concatenate(J_history)
J_history = np.array(cost)

arr = np.array(w_history)
w1_history = np.array(arr[:,0])
w2_history = np.array(arr[:,1])

可视化

fig= plt.figure(figsize=(20,8))
plt.plot(range(iterations),J_history)
plt.title("cost vs. iterations")
plt.xlabel("iterations")
plt.ylabel("cost")
plt.show()

fig1 = plt.figure()
ax = fig1.add_subplot(111, projection='3d')

ax.scatter(w1_history, w2_history, J_history)
ax.set_title("w1,w2 vs. cost")
ax.set_xlabel('w1')
ax.set_ylabel('w2')
ax.set_zlabel('w3')
plt.show()

### 决策边界
plot_decision_boundary(w, b, x_train, y_train)

2.8 评估逻辑回归

我们可以通过查看学习模型在训练集上的预测能力来评估我们找到的参数的质量。
你需要在以下代码中实现 predict 函数以完成这个任务。
请完成 predict 函数，根据给定的数据集和学习得到的参数向量 $w$ 和截距 $b$，产生二元分类器的预测结果 0 或 1。

• 首先，需要对模型的每个样本计算预测值 $f(x^{(i)})=g(w\cdot x^{(i)})$

  • 在之前的部分中，您已经实现了这一步骤。

• 我们将模型的输出（$f(x^{(i)})$）解释为在给定的参数 $w$ 下，$y^{(i)}=1$ 的概率。

• 因此，要从逻辑回归模型中得出最终的预测结果（$y^{(i)}=0$ 或 $y^{(i)}=1$），可以使用以下启发式方法：

  如果 $f(x^{(i)})>=0.5$，则预测 $y^{(i)}=1`

  如果 $f(x^{(i)})<0.5$，则预测 $y^{(i)}=0`

def predict(x,w,b):
    m = x.shape[0]
    p = np.zeros(m)
    for i in range(m):
        z_wb = np.dot(x[i],w)+b
        f_wb = sigmod(z_wb)
        p[i] = 1 if f_wb>0.5 else 0
    return p

p = predict(x_train, w,b)
print('训练准确度: %f'%(np.mean(p == y_train) * 100))

训练准确度: 92.000000

3、 正则化逻辑回归

在本部分练习中，您将实现正则化逻辑回归来预测制造工厂的微芯片是否通过质量保证（QA）。在 QA 过程中，每个微芯片都要经过各种测试以确保其正常运行。

3.1 问题陈述

假设您是该工厂的产品经理，并且您拥有一些微芯片的两个不同测试的测试结果。

• 从这两个测试中，您想确定这些微芯片是否应被接受或拒绝。
• 为了帮助您做出决定，您拥有过去微芯片的测试结果数据集，可以建立一个逻辑回归模型。

3.2 加载和可视化数据

与此练习的先前部分类似，让我们从加载此任务的数据集并将其可视化开始。

• 下面显示的 load_dataset() 函数将数据加载到变量 X_train 和 y_train 中
  • X_train 包含来自两个测试的微芯片的测试结果
  • y_train 包含 QA 的结果
    • 如果微芯片被接受，则 y_train = 1
    • 如果微芯片被拒绝，则 y_train = 0
  • X_train 和 y_train 都是 numpy 数组。

X_train, y_train = load_data("data/ex2data2.txt")

plot_data(X_train, y_train[:], pos_label="Accepted", neg_label="Rejected")
plt.rcParams['axes.unicode_minus']=False
# Set the y-axis label
plt.ylabel('Microchip Test 2')
# Set the x-axis label
plt.xlabel('Microchip Test 1')
plt.legend(loc="upper right")
plt.show()

图 3 显示，我们的数据集不能通过一条直线将图分为正示例和负示例。因此，逻辑回归的直接应用在此数据集上表现不佳，因为逻辑回归只能找到线性决策边界。

3.3 特征映射

使数据拟合得更好的一种方法是从每个数据点创建更多特征。在提供的函数 map_feature 中，我们将把特征映射为 $x_1$ 和 $x_2$ 的所有多项式项，最高次幂为 6。

m a p _ f e a t u r e ( x ) = [ x 1 x 2 x 1 2 x 1 x 2 x 2 2 x 1 3 ⋮ x 1 x 2 5 x 2 6 ] \mathrm{map\_feature}(x) = \left[\begin{array}{c} x_1\\ x_2\\ x_1^2\\ x_1 x_2\\ x_2^2\\ x_1^3\\ \vdots\\ x_1 x_2^5\\ x_2^6\end{array}\right] map_feature(x)= ​x1​x2​x12​x1​x2​x22​x13​⋮x1​x25​x26​​ ​

由于这种映射，我们的两个特征（两次 QA 测试的分数）的向量已被转换为一个 27 维向量。

• 在这个更高维度的特征向量上训练的逻辑回归分类器将具有更复杂的决策边界，并且在我们的二维图中绘制时将是非线性的。
• 我们在 utils.py 文件中为您提供了 map_feature 函数。

print("初维度:", X_train.shape)

mapped_X =  map_feature(X_train[:, 0], X_train[:, 1])
print("映射后维度:", mapped_X.shape)

初维度: (118, 2)
映射后维度: (118, 27)

虽然特征映射可以让我们构建一个更具表现力的分类器，但它也更容易过拟合。在接下来的练习中，您将实现正则化逻辑回归来拟合数据，并亲自看看正则化如何帮助解决过拟合问题。

3.4 正则化逻辑回归的代价函数

在这一部分中，您将实现正则化逻辑回归的代价函数。

回想一下，对于正则化逻辑回归，代价函数的形式如下：
$$J(\mathbf{w},b)=\frac{1}{m}\sum _{i=0}^{m-1}\left[-y^{(i)}\log \left(f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)-\left(1-y^{(i)}\right)\log \left(1-f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)\right]+\frac{\lambda }{2m}\sum _{j=0}^{n-1}{w}_j^2$$

将此与没有正则化的代价函数（您上面实现的）进行比较，其形式为

$$J(\mathbf{w}.b)=\frac{1}{m}\sum _{i=0}^{m-1}\left[(-y^{(i)}\log \left(f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)-\left(1-y^{(i)}\right)\log \left(1-f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)\right]$$

它们的区别在于正则化项，即$$\frac{\lambda }{2m}\sum _{j=0}^{n-1}{w}_j^2$$
请注意，$b$参数不会被正则化。

请完成下面的 compute_cost_reg 函数，以计算
w 中每个元素的以下术语：

$$\frac{\lambda }{2m}\sum _{j=0}^{n-1}{w}_j^2$$
然后，起始代码将此添加到没有正则化的成本（您在 compute_cost 中计算的）中，以计算具有正则化的成本。

def compute_cost_reg(x,y,w,b,lambda_=1):
    m =x.shape[0]
    cost_without_reg = compute_cost(x, y, w, b)
    reg_cost = sum(np.square(w))
    total_cost = cost_without_reg + (lambda_/(2 * m)) * reg_cost
    return total_cost

3.5 正则化 logistic 回归的梯度

在本节中，您将实现正则化 logistic 回归的梯度。

正则化代价函数的梯度有两个组成部分。第一个部分 $\frac{\partial J(\mathbf{w},b)}{\partial b}$ 是一个标量，另一个部分是一个与参数 $\mathbf{w}$ 形状相同的向量，其中第 j 个元素定义如下：

$$\frac{\partial J(\mathbf{w},b)}{\partial b}=\frac{1}{m}\sum _{i=0}^{m-1}(f_{\mathbf{w},b}({\mathbf{x}}^{(i)})-y^{(i)})$$

KaTeX parse error: Undefined control sequence: \mbox at position 184: …} w_j \quad\, \̲m̲b̲o̲x̲{for $j=0...(n-…

将此与没有正则化的代价函数的梯度进行比较（上面已经实现过），其形式为

$$\frac{\partial J(\mathbf{w},b)}{\partial b}=\frac{1}{m}\sum _{i=0}^{m-1}(f_{\mathbf{w},b}({\mathbf{x}}^{(i)})-{\mathbf{y}}^{(i)})\text{\hspace{1em}(2)}$$
$$\frac{\partial J(\mathbf{w},b)}{\partial w_j}=\frac{1}{m}\sum _{i=0}^{m-1}(f_{\mathbf{w},b}({\mathbf{x}}^{(i)})-{\mathbf{y}}^{(i)})x_j^{(i)}\text{\hspace{1em}(3)}$$

可以看出，$\frac{\partial J(\mathbf{w},b)}{\partial b}$ 是相同的，不同之处在于 $\frac{\partial J(\mathbf{w},b)}{\partial w}$ 中的以下项：

KaTeX parse error: Undefined control sequence: \mbox at position 32: …} w_j \quad\, \̲m̲b̲o̲x̲{for $j=0...(n-…

def compute_gradient_reg(x,y,w,b,lambda_):
    m,n = x.shape
    dj_dw,dj_db = compute_gradient(x,y,w,b)
    for i in range(n):
        dj_dw[i] += (lambda_/m)*w[i]
    return dj_dw,dj_db

3.6 正则梯度下降

与前面的部分类似，您将使用上面实现的梯度下降函数来学习最优参数$w$,$b$。

• 如果您已正确完成正则化逻辑回归的成本和梯度计算，您应该能够通过下一个单元格逐步学习参数$w$。
• 在训练完参数之后，我们将使用它来绘制决策边界。

注意

下面的代码块运行时间相当长，特别是对于非矢量化版本。您可以减少iterations以测试您的实现并更快地迭代。如果您有时间，请运行100,000次迭代以获得更好的结果。

def gradient_descent_reg(x,y,w_in,b_in,cost_function,gradient,alpha,num_iters,lambda_):
    w = copy.deepcopy(w_in)
    b = b_in
    J_history = []
    w_history = []
    for i in range(num_iters):
        dj_dw,dj_db = gradient(x,y,w,b)
        w -= alpha* dj_dw
        b -= alpha* dj_db
        cost = cost_function(x,y,w,b)
        J_history.append(cost)
        w_history.append([wi.copy() for wi in w])
    return w,b,J_history,w_history

np.random.seed(1)
initial_w = np.random.rand(mapped_X.shape[1])-0.5
initial_b = 1.

# Set regularization parameter lambda_ to 1 (you can try varying this)
lambda_ = 0.01
# Some gradient descent settings
iterations = 10000
alpha = 0.01

w,b, J_history,_ = gradient_descent_reg(mapped_X, y_train, initial_w, initial_b,
                                    compute_cost_reg, compute_gradient_reg,
                                    alpha, iterations, lambda_)

3.7 绘制决策边界

为了帮助您可视化该分类器所学习的模型，我们将使用 plot_decision_boundary 函数来绘制（非线性）决策边界，该边界将正例和负例分开。

• 在函数中，我们通过计算分类器对均匀间隔网格上的预测，然后绘制从 y = 0 到 y = 1 的预测变化的轮廓图，来绘制非线性决策边界。

• 在学习参数 $w$、$b$ 后，下一步是绘制决策边界。

plot_decision_boundary(w, b, mapped_X, y_train)

​

​

3.8 评估正则化逻辑回归模型

您将使用上面实现的 predict 函数来计算正则化逻辑回归模型在训练集上的准确度。

p = predict(mapped_X, w, b)

print('训练准确率: %f'%(np.mean(p == y_train) * 100))

训练准确率: 82.203390