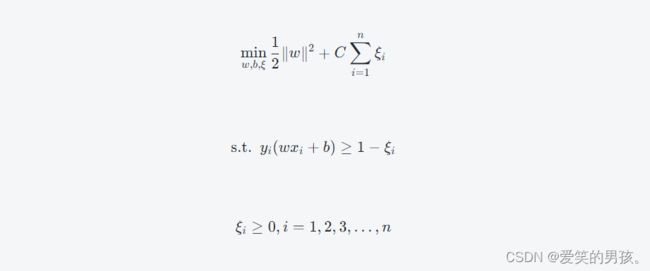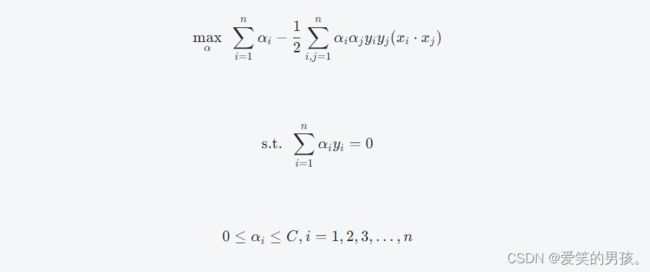【机器学习】十大算法之一 “SVM”

 

作者主页：爱笑的男孩。的博客_CSDN博客-深度学习,活动,python领域博主爱笑的男孩。擅长深度学习,活动,python,等方面的知识,爱笑的男孩。关注算法,python,计算机视觉,图像处理,深度学习,pytorch,神经网络,opencv领域.https://blog.csdn.net/Code_and516?type=blog个人简介：打工人。

持续分享：机器学习、深度学习、python相关内容、日常BUG解决方法及Windows&Linux实践小技巧。

如发现文章有误，麻烦请指出，我会及时去纠正。有其他需要可以私信我或者发我邮箱:[email protected] 

        

        机器学习算法种类繁多，SVM支持向量机算法是其中十大常用算法之一。该算法起源于20世纪80年代，并在90年代逐渐形成了比较完整的理论体系和工程应用。该算法在分类领域有着广泛的应用，并在多项应用场景中表现出了较优的性能。

本文讲详细讲解机器学习十大算法之一“SVM”

---

目录

一、简介

二、SVM的发展史

三、SVM算法公式讲解

四、SVM的算法原理

        1. 高效

        2. 对样本大小不敏感

        3. 可以通过核函数处理非线性分类问题

        4. 对边缘数据敏感

五、SVM算法的功能

        1. 分类问题

        2. 回归问题

        3. 异常检测

六、示例代码

        1. 实现一个简单的线性SVM模型

        2. 实现一个带核函数的SVM模型

七、总结

---

一、简介

        支持向量机（Support Vector Machine，SVM）是机器学习十大算法之一，是一种二分类模型。SVM将实例空间映射到一个高维空间，将空间进行线性划分，同时使得分类面到两端最近的数据点的距离（margin）最大化，因此SVM也被称为最大间隔分类器（Maximal Margin Classifier）。SVM是由Vapnik和Cortes于1995年提出的，是一种广泛应用的机器学习算法，具有很好的泛化能力和鲁棒性。

二、SVM的发展史

        SVM算法是由Vapnik等人于1995年提出的。Vapnik等人早在1982年就开始了支持向量机的研究工作。SVM最初是被应用于二元分类问题，后来发展成可以用于多元分类、回归分析和异常检测等领域。

        SVM在很长一段时间内由于其算法复杂度高、理论不足、实际应用受限等问题，挣扎着发展。直到20世纪90年代期初，SVM才经过若干改进，达到了一个比较成熟的阶段。同时，大量的工作表明，SVM是非常成功的分类器，并在模式识别、计算机视觉、自然语言处理等领域得到广泛应用。

三、SVM算法公式讲解

        下面我们介绍一下SVM的算法公式和其背后的意义。

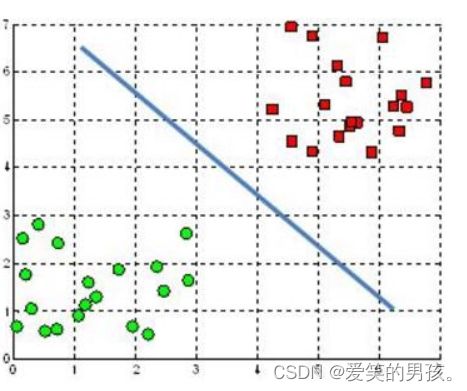
        在SVM中，我们首先需要根据训练数据构建一个超平面（Hyperplane），以此来分隔数据。超平面是在空间中将不同类别的数据分开的一条直线或曲面。如图所示，绿色和红色点表示两类数据，直线为超平面。

        超平面的数学定义为：每个样本点(xi​,yi​) 有yi​(wxi​+b)≥1，其中w表示超平面的法向量，b表示截距，yi​表示样本的标签。

        在上述公式中，当数据是线性可分时，我们可以找到一条相对于所有其他直线都是最优的分类直线，这条直线就被称为间隔最大化超平面（Maximum Margin Hyperplane，MMH）。寻找最优分割线的过程就是一个最优化问题，此时SVM就被定义为通过最大化一定间隔来实现分类的一种线性分类器。

        当数据不是完全线性可分时，我们就需要引入松弛变量（Slack Variable）\xiξ。超过最大间隔（Margin）的样本点它们的\xiξ值将大于1。我们需要找到一个平衡点，让所有误分类点尽量多地分在同一侧，并且最大化间隔，同时降低\xiξ值。具体来说，我们需要找到一个平衡\xiξ值和分类准确率的点，在这个点上，我们既能够达到最大间隔，又不会牺牲太多的分类准确率。这样的分类器我们称为软间隔SVM。

        在经过优化后，最终SVM的目标函数可以表示为：

        目标函数的第一项表示最小化模长，这个代表了要寻找一个“干净”的分割线。如果不考虑约束条件，我们会找到能够将训练样本点完美分隔的超平面，但是这样的超平面在未来可能会得到较差的结果。第二项是异常点的正则化项，它表示决策面的复杂度。CC是一个超参数，用于在最小化第一项和第二项之间找到一个合适的平衡点。

        通过对目标函数进行拉格朗日乘子法（Lagrange Multiplier）的变换，我们可以获得SVM的对偶形式：

         其中，αi​是拉格朗日乘子，x⋅y表示向量x和y的内积，即x⋅y=∣∣x∣∣⋅∣∣y∣∣cos(θ)，∣∣x∣∣表示向量x的模长，θ表示向量x和y的夹角。

        它与原始问题的解等价，并且通常在实践中使用对偶形式来解决超大规模的问题。求得α向量后，我们可以使用以下公式来预测测试数据的类别：

        其中，t为测试样本。

四、SVM的算法原理

        SVM的原理并不复杂，其主要思想是：如果两类数据可以用一个超平面有效地分割，那么SVM就寻找一个最大化分类间隔的超平面。这个分类间隔是指两个类之间的距离，也就是超平面两侧到最近数据点的距离之和。因此，SVM真正的目标是求得最大间隔的超平面（即MMH），以便最大程度地提高泛化性能。当数据不是完全线性可分时，SVM会引入松弛变量，从而得到一个平衡点，以降低误分类数据点的影响，这样的SVM就是软间隔SVM。同时，SVM可以通过使用核函数来处理非线性问题。

        SVM算法的主要特征包括以下几个方面：

        1. 高效

        SVM是一种高效的算法，其能够对高维空间中的数据进行分类工作。它的运算的复杂度与训练数据的点的数量有关，而与维度无关。

        2. 对样本大小不敏感

        SVM算法的采用与样本规模的大小无关，并且在小样本集中非常高效，这个算法著名的维度灾难（Curse of Dimensionality）只影响高维空间中样本数量过多的情况。

        3. 可以通过核函数处理非线性分类问题

        SVM算法通过引入核函数来处理非线性性分类问题，这种方法被称为非线性SVM（nonlinear SVMs）。

        4. 对边缘数据敏感

        SVM算法的预测依赖于少数的边缘数据点，这些点被称为支持向量（Support Vectors）。

五、SVM算法的功能

        SVM主要用于分类问题、回归问题和异常检测等领域。

        1. 分类问题

        SVM的核心思想是找到一个超平面来最大化分类间隔，SVM可以解决线性和非线性分类问题，在二元和多元分类问题上的表现优秀。

        2. 回归问题

        SVM同时也是一种基于统计学习理论的回归分析方法。它通过最小化预测误差和最大化分类间隔来处理回归问题。

        3. 异常检测

        在异常检测中，SVM可以发现一个在高维空间中的数据子集，该子集拥有异常成员。本质上，这是一个在多维标准（multivariate criterion）空间中寻找一个超平面的问题，这个问题可以被转化为一个带约束的优化问题。

六、示例代码

        下面我们将使用Python来展示一个简单的SVM分类器的实现，并对其进行简单的测试。

        首先，我们需要导入以下库：

from sklearn import svm, datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
import numpy as np

        1. 实现一个简单的线性SVM模型

        下面，我们将使用Python的SVM库，实现一个简单的线性SVM模型。在这个模型中，我们将使用鸢尾花数据集（Iris dataset）来进行分类。

# 加载数据集
iris = datasets.load_iris()
X = iris.data[:, :2]
y = iris.target
 
# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42)

# 创建模型
clf = svm.SVC(kernel='linear')
 
# 训练模型
clf.fit(X_train, y_train)
 
# 预测
y_pred = clf.predict(X_test)

# 计算准确率
acc = accuracy_score(y_test, y_pred)
print("Accuracy: ", acc)

结果：

Accuracy: 0.7555555555555555

        2. 实现一个带核函数的SVM模型

        下面，我们将使用Python来实现一个带有核函数的SVM模型。

# 加载数据集
X, y = datasets.make_circles(n_samples=300, factor=.3, noise=.05)

# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, 
                        test_size=0.3, random_state=42)
 
# 创建模型
clf = svm.SVC(kernel='rbf', gamma=0.7)
 
# 训练模型
clf.fit(X_train, y_train)
 
# 预测
y_pred = clf.predict(X_test)

# 计算准确率
acc = accuracy_score(y_test, y_pred)
print("Accuracy: ", acc)

结果：

Accuracy:  1.0

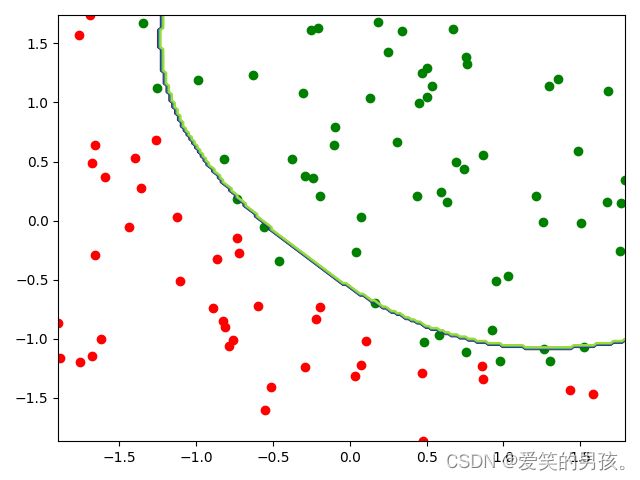
        这是一个非线性问题，但是我们通过使用径向基函数（Radial basis function）来找到了一个非常好的解。

七、总结

        SVM是一种非常有用的算法，它在分类和回归问题中都表现出色。SVM的主要思想是找到一个良好的决策边界，以便正确地将数据分类。 SVM使用支持向量来确定边界，这些支持向量是从训练数据中选择的。

        SVM算法可以用于二元分类和多类别分类问题，可以使用不同的核函数来解决非线性问题。有许多SVM变种，包括核SVM，线性SVM和非线性SVM。 SVM还可以处理大规模问题，具体方法是通过适当的技术简化问题。

        总之，SVM算法是机器学习中非常重要的算法之一，它通过优化一个目标函数，找到最佳的决策边界。 SVM算法可以用于许多不同的问题，在许多不同的领域被广泛应用，因此对它的研究和应用具有非常重要的价值。