Computer Graphics From Scratch - Chapter 2

系列文章目录

简介： Computer Graphics From Scratch-《从零开始的计算机图形学》简介
第一章: Computer Graphics From Scratch - Chapter 1 介绍性概念

---

---

Basic Raytracing - 基本光线追踪

在本章中，我们将介绍光线追踪，这是我们将介绍的第一个主要算法。

我们首先激发算法并布置一些基本的伪代码。
然后我们看看如何在场景中表示光线和物体。
最后，我们推导出一种方法来计算哪些光线构成了场景中每个对象的可见图像，并看看我们如何在画布上表示它们。

---

一、渲染瑞士风景

假设您正在访问一些异国情调的地方，并遇到了令人惊叹的风景-如此令人惊叹，您只需要制作一幅画来捕捉它的美丽。 图 2-1 显示了这样一种情况。

图 2-1：令人叹为观止的瑞士风景

你有画布和画笔，但你绝对缺乏艺术天赋。 所有的希望都失去了吗？

不必要地。 你可能没有艺术天分，但你有条不紊。 所以你做了最明显的事情：你得到一个昆虫网【类似于像素网格一样】。 你剪下一块长方形，把它框起来，然后把它固定在一根棍子上。 现在您可以通过网状窗口查看景观。 接下来，您选择最佳视角来欣赏这片风景，并种植另一根棍子来标记您的眼睛应该在的确切位置。

你还没有开始画，但现在你有了一个固定的视角和一个固定的框架，你可以通过它看到风景。 而且，这个固定的框架被昆虫网分成小方块。 现在是有条理的部分。 你在画布上画了一个网格，给它与昆虫网相同数量的正方形。 然后你看一下网的左上角。 你能透过它看到的主要颜色是什么？ 天蓝色。 所以你把画布的左上角画成天蓝色。 你对每个正方形都这样做，很快画布就包含了一幅相当不错的风景画，正如从框架中看到的那样。 生成的绘画如图 2-2 所示。

图 2-2：粗略的近似景观

---

仔细想想，计算机本质上是一台非常有条理的机器，绝对缺乏艺术天赋。 我们可以描述创建我们的绘画的过程如下：

For each little square on the canvas
	Paint it the right color

对于画布上的每个小方块
	涂上合适的颜色

---

简单的！ 但是，该公式过于抽象，无法直接在计算机上实现。 我们可以更详细一点：

Place the eye and the frame as desired
For each square on the canvas
	Determine which square on the grid corresponds to this square on the canvas
	Determine the color seen through that grid square
	Paint the square with that color

根据需要放置眼睛和框架
对于画布上的每个正方形
	确定网格上的哪个正方形对应于画布上的这个正方形
	确定通过那个方格看到的颜色
	用那种颜色画正方形

---

这仍然太抽象了，但它开始看起来像一种算法——也许令人惊讶的是，这是对完整光线追踪算法的高级概述！ 是的，就是这么简单。

---

二、基本假设

计算机图形学的部分魅力在于在屏幕上绘图。 为了尽快实现这一点，我们将做一些简化的假设。

当然，这些假设对我们能做什么施加了一些限制，但我们将在后面的章节中解除这些限制。

首先，我们将假设一个固定的观看位置。 观看位置，即在瑞士风景类比中您将视线放在的位置，通常称为相机位置； 让我们称之为 O。我们假设相机占据空间中的一个点，它位于坐标系的原点，并且它永远不会从那里移动，所以 O = (0, 0, 0 ） 目前。

其次，我们将假设一个固定的相机方向。 相机方向决定了相机指向的位置。 我们假设它朝 Z 轴正方向（我们将其缩短为$Z_{+}$ ），Y 轴正方向 ($Y_{+}$) 向上，X 轴正方向 ($X_{+}$) 向右（图 2-3）

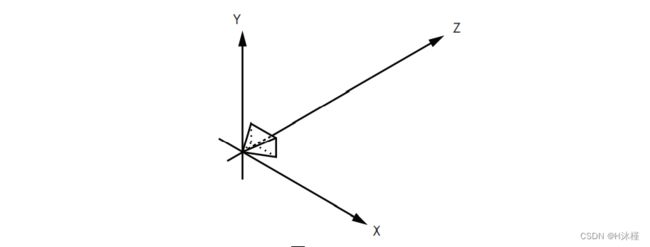
图 2-3. 相机的位置和方向

---

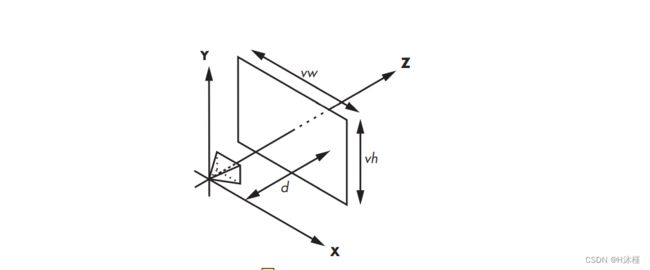
相机位置和方向现在是固定的。 类比中仍然缺少我们观察场景的“框架”。 我们假设这个框架的尺寸为 $V_w$ 和 $V_h$ ，并且正对相机方向，即垂直于 $Z_{+}$。我们还假设它在一定距离 $d$ 处，它的边平行于 X 和 Y 轴，并且相对$Z$ 居中。 这很拗口，但实际上很简单。 请看图 2-4。

将作为我们通往世界的窗口的矩形称为视口。 本质上，我们将在画布上绘制通过视口看到的任何东西。 请注意，视口的大小和到相机的距离决定了从相机可见的角度，称为视野，或简称 FOV。 人类有近 180° 的水平 FOV（尽管其中大部分是模糊的周边视觉，没有深度感）。 为简单起见，我们将设置 $V_w$ = $V_h$ = $d$ = 1； 这会产生大约 53° 的 FOV，从而生成外观合理且不会过度失真的图像。

图 2-4 视口的位置和方向

让我们回到前面介绍的“算法”，使用适当的技术术语，并对示例 2-1 中的步骤进行编号。

❶ Place the camera and the viewport as desired
For each pixel on the canvas
❷ Determine which square on the viewport corresponds to this pixel
❸ Determine the color seen through that square
❹ Paint the pixel with that color

❶ 根据需要放置相机和视口
对于画布上的每个像素
❷ 确定视口上哪个方块对应这个像素
❸ 确定透过那个正方形看到的颜色
❹ 用该颜色绘制像素

示例2-1：我们的光线追踪算法的高级描述

我们刚刚完成了步骤❶（或者，更准确地说，暂时将其排除在外）。 步骤❹很简单：我们只需使用 canvas.PutPixel(x, y, color)。 让我们快速执行步骤❷，然后在接下来的几章中将注意力集中在执行步骤❸的越来越复杂的方法上。

---

附：markdown在字母上表示向量，上横线，下横线，上尖，上波浪线，一阶导数，二阶导数。

$\vec{a}$  向量
$\overline{a}$ 平均值
$\underline{a}$下横线
$\widehat{a}$ (线性回归，直线方程) y尖
$\widetilde{a}$ 颚化符号  等价无穷小
$\dot{a}$   一阶导数
$\ddot{a}$  二阶导数
$\frac{分子}{分母}$:

$a$ 向量
$\overline{a}$ 平均值
$\underline{a}$下横线
$a$ (线性回归，直线方程) y尖
$a$ 颚化符号 等价无穷小
$\dot{a}$ 一阶导数
$\ddot{a}$ 二阶导数
$\frac{分子}{分母}$:

---

三、画布到视口

示例2-1 中算法的第 ❷ 步要求我们确定视口上的哪个正方形对应于该像素。 我们知道像素的画布坐标——我们称它们为 $C_x$ 和 $C_y$。 请注意我们如何方便地放置视口，使其轴与画布的方向匹配，并且其中心与画布的中心匹配。 因为视口是用世界单位测量的，而画布是用像素测量的，所以从画布坐标到空间坐标只是比例的变化！
$$Vx=Cx\cdot \frac{Vw}{Cw}$$
$$Vy=Cy\cdot \frac{Vh}{Ch}$$

---

还有一个额外的细节。虽然视窗是2D 的，但它嵌入在3D 空间中。我们定义它与摄像机的距离为 $d$ ; 根据定义，这个平面上的每个点(称为投影平面)都有 z = d。因此，
$$Vz=d$$

---

我们完成了这一步。 对于画布上的每个像素$(Cx,Cy)$，我们可以确定它在视口上的对应点$(Vx,Vy,Vz)$。

---

四、追踪光线

下一步是确定从相机的角度$(Ox,Oy,Oz)$看到的通过 $(Vx,Vy,Vz)$ 的光是什么颜色。

在现实世界中，光来自光源（太阳、灯泡等），从多个物体反射回来，最后到达我们的眼睛。 我们可以尝试模拟每个光子离开模拟光源的路径，但这会非常耗时。 我们不仅要模拟数量惊人的光子（一个 100 W 的灯泡每秒发射 10²⁰ 个光子！），在通过视口后，它们中只有极少数会碰巧到达 $(Ox,Oy,Oz)$。 这种技术称为光子追踪或光子映射； 不幸的是，这超出了本书的范围。

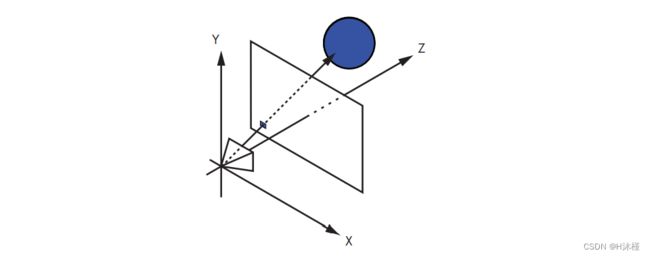
相反，我们将“反向”考虑光线； 我们将从来自相机的光线开始，穿过视口中的一个点，并跟踪它的路径，直到它碰到场景中的某个对象。 这个对象是相机通过视口的那个点“看到”的东西。 因此，作为第一个近似值，我们只需将该对象的颜色作为“通过该点的光的颜色”，如图 2-5 所示。

图 2-5. 视口中的一个小方块，代表画布中的单个像素，涂有相机通过它看到的对象的颜色

现在我们只需要一些方程。

---

4.1. 射线方程

就我们的目的而言，表示射线的最方便的方法是使用参数方程。 我们知道射线穿过 $O$，并且我们知道它的方向（从 $O$ 到 $V$），所以我们可以将射线中的任意点 $P$ 表示为
$$P=O+t(V–O)$$
其中 t 是任何实数。 通过将 $t$ 从 $–\infty$ 到 $+\infty$ 的每个值代入该方程，我们得到沿射线的每个点 $P$。

我们称 $(V–O)$，射线的方向，$D$。 方程变为
$$P=O+tD$$

理解这个方程的一种直观方法是，
我们从原点 ($O$) 开始射线，
然后 沿着射线的方向 ($D$) “前进”一定量 ($t$)；
很容易看出沿着射线的所有点。
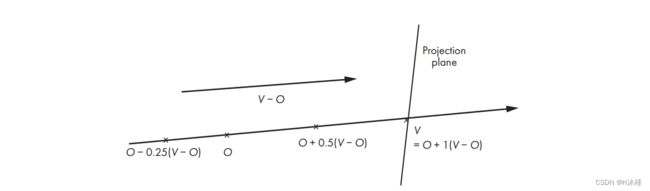
您可以在线性代数附录中阅读有关这些向量运算的更多详细信息。 图 2-6 显示了我们的方程。

图 2-6：对于不同的 t 值，射线 $O+tD$ 的一些点。

图 2-6 显示了对应于 $t$ = 0.5 和 $t$ = 1.0 的射线上的点。 $t$ 的每个值都会沿射线产生不同的点。

---

4.2. 球面方程

现在我们需要在场景中有某种对象，以便我们的光线可以击中某些东西。 我们可以选择任意几何图元作为场景的构建块； 对于光线追踪，我们将使用球体，因为它们很容易用方程处理。

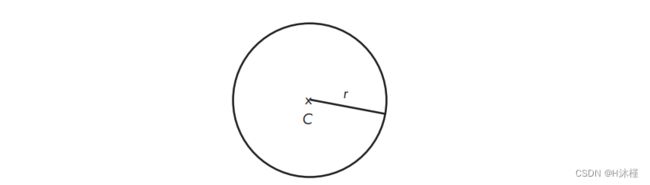
什么是球体？ 球体是与固定点相距固定距离的一组点。 该距离称为球体的半径，该点称为球体的中心。 图 2-7 显示了一个球体，由其中心 $C$ 和半径 $r$ 定义。

图 2-7：一个球体，由其中心和半径定义

根据我们上面的定义，如果 $C$ 是球的中心，$r$ 是球的半径，则该球表面上的点 $P$ 必须满足以下等式：
$$distance(P,C)=r$$
让我们展开一下这个等式。 如果您发现其中任何数学不熟悉，请通读线性代数附录。
$P$ 和 $C$ 之间的距离是从 $P$ 到 $C$ 的向量的长度：
$$|P–C|=r$$
向量的长度（表示为|$V$|）是其与自身的点积的平方根（表示为$<V,V>$):
$$\sqrt{⟨P–C,P–C⟩}=r$$
注：

• 内积：点积、点乘、数量积（标量积）。表示结果为一个标量（数）的乘法。
• 外积：叉积、叉乘、向量积

为了摆脱平方根，我们可以将两边平方：
$$⟨P–C,P–C⟩=r^2$$
球体方程的所有这些公式都是等价的，但最后一个是在以下步骤中最方便操作的。

---

4.3. 射线遇到球体

我们现在有两个方程：一个描述球体上的点，一个描述射线上的点：
$$⟨P–C,P–C⟩=r^2$$
$$P=O+tD$$
射线和球体相交吗？ 如果有，在哪里？

假设射线和球体在点 $P$ 相交。这个点既沿着射线又在球体的表面上，所以它必须同时满足两个方程。 请注意，这些方程中唯一的变量是参数 $t$，因为 $O$、$D$、$C$ 和 $r$ 已给出，而 $P$ 是我们试图找到的点。

由于 $P$ 在两个方程中表示相同的点，我们可以将第一个方程中的 $P$ 替换为第二个方程中 $P$ 的表达式。 代入得到等式：
$$⟨O+tD–C,O+tD–C⟩=r^2$$

如果我们能找到满足这个方程的 $t$ 值，我们可以将它们放入射线方程中以找到射线与球体相交的点。

在目前的形式中，这个方程有点笨拙。 让我们做一些代数操作，看看我们能从中得到什么。

首先，让 $CO=O–C$。然后我们可以将方程写为
$$⟨CO+tD,CO+tD⟩=r^2$$

然后我们将点积扩展成它的分量，利用它的分布特性（同样，请随时查阅线性代数附录）
$$⟨CO+tD,CO⟩+⟨CO+tD,tD⟩=r^2$$
$$⟨CO,CO⟩+⟨tD,CO⟩+⟨CO,tD⟩+⟨tD,tD⟩=r^2$$
重新排列术语，整理后，我们得到
$$⟨tD,tD⟩+2⟨CO,tD⟩+⟨CO,CO⟩=r^2$$

将参数 $t$ 从点积中移出并将 $r2$ 移到等式的另一边, 给出了我们
$$t^2⟨D,D⟩+t(2⟨CO,D⟩)+⟨CO,CO⟩-r^2=0$$

请记住，两个向量的点积是实数，因此尖括号之间的每一项都是实数。 如果我们给它们起名字，我们会得到更熟悉的东西：
$$a=⟨D,D⟩$$
$$b=2⟨CO,D⟩$$
$$c=⟨CO,CO⟩-r^2$$
整体代换得：
$$a{t}^2+bt+c=0$$
这只不过是一个很好的二次方程！[如同我们之前学过得一元二次方程一样] 它的解是射线与球体相交的参数 $t$ 的值：
$$\{t1,t2\}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

4.3.1 附：上面计算细节：

• 射线方程：
  射线从$O$到$V$，
  $O$是原点(相机的角度，坐标为($O_x,O_y,O_z$ )；
  $V$是视口，也就是相机$Z$轴正向前方的一个平面，坐标为($V_x,V_y,V_z$ )；
  那么射线上任意点$P$可以表示为:
  $$P=O+t(V-O)$$
  其中$t$是任何实数，是一个变量；
  将$(V-O)$，射线的方向，设为$D$ ;
  则方程为
  $$P=O+tD$$
  $$OP=O+tD$$
  综上，得：
  $$OP=tD$$

---

• 球面方程：
  $C$为圆心，$r$为半径，$P$是球上一点
  则：$$|OP-OC|=r$$
  不论是点$P$到点$C$的距离，还是点$C$到点$P$的距离都是半径$r$;
  $$|OC-OP|=r$$
  又因为
  $OP-OC=CP$ //根据向量的减法
  $OC-OP=PC$
  后面统一写$CP$

得：
$$|CP|=r$$
又因为$CP$的长度是其与自身点积的平方根：
$$|CP{|}^2=CP\cdot CP$$
或 $$|CP|=\sqrt{CP\cdot CP}$$
所以：
$$\sqrt{CP\cdot CP}=r$$
或 $$CP\cdot CP=r^2$$

---

• 射线方程结合球面方程：
  $$\{\begin{array}{l}OP=tD---①\\ CP\cdot CP=r^2---②\\ OP-OC=CP---③\end{array}$$
  将①和③式代入②中，得：
  $$(tD-OC)\cdot (tD-OC)=r^2$$
  转换为加法，得：
  $$(tD+CO)\cdot (tD+CO)=r^2$$
  向量满足交换律，得：
  $$(CO+tD)\cdot (CO+tD)=r^2$$

---

附：

$$a=(x_1,y_1)$$ $$b=(x_2,y_2)$$
$$a\cdot b=x_1\ast x_2+y_1\ast y_2$$
$$a\cdot b=|a|\ast |b|\ast \cos (\theta )$$
$$a\cdot (\gamma b)=\gamma (a\cdot b)$$ \\与数的结合律，$\gamma$是实数
$$a\cdot b=b\cdot a$$ \\点积(内积)的向量交换律
.$$a\cdot (b+c)=a\cdot b+a\cdot c$$ \\点积(内积)的向量分配律

---

将点积扩展成它的分量，利用它的分布特性，得：
$$(CO+tD)\cdot CO+(CO+tD)\cdot (tD)=r^2$$
又因为点积(内积)的向量分配律，得：
$$CO\cdot CO+tD\cdot CO+CO\cdot tD+tD\cdot tD=r^2$$
又点积(内积)的向量交换律，得：
$$CO\cdot CO+CO\cdot tD+CO\cdot tD+tD\cdot tD=r^2$$
即：
$$tD\cdot tD+2CO\cdot tD+CO\cdot CO=r^2$$
又与数的结合律，得：
$$t^2(D\cdot D)+t(2(CO\cdot D))+CO\cdot CO=r^2$$
整理得：
$$t^2(D\cdot D)+t(2(CO\cdot D))+(CO\cdot CO-r^2)=0$$

---

两个向量的点积是实数
另：
$$\{\begin{array}{l}a=D\cdot D---①\\ b=2(CO\cdot D)---②\\ c=CO\cdot CO-r^2---③\end{array}$$
整体代换，得：
$$a{t}^2+bt+c=0$$

它的解是射线与球体相交的参数$t$ 的值：
$$\{t1,t2\}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

---

---

幸运的是，这具有几何意义。
您可能还记得，根据判别式 $b^2-4ac$ 的值，二次方程可以没有解、一个双重解或两个不同的解。
这正好对应于光线不与球体相交、光线与球体相切以及光线分别进入和离开球体的情况（图 2-8）。

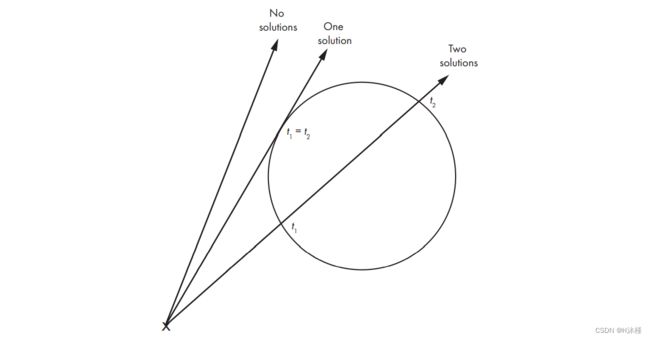
图 2-8：二次方程解的几何解释：无解、一个解或两个解。

一旦我们找到了 $t$ 的值，我们就可以将它代入射线方程，最终得到与 $t$ 的值对应的交点$P$。

---

五、渲染我们的第一个球体

回顾一下，对于画布上的每个像素，我们可以计算视口上的对应点。 给定相机的位置，我们可以表达从相机开始并穿过视口该点的光线方程。 给定一个球体，我们可以计算光线与该球体相交的位置。

所以我们需要做的就是计算光线和每个球体的交点，保持交点离相机最近，然后用适当的颜色在画布上绘制像素。 我们几乎准备好渲染我们的第一个球体了！

---

不过，参数 $t$ 值得特别注意。 让我们回到射线方程：
$$P=O+t(V–O)$$
由于射线的原点和方向是固定的，因此在所有实数上改变 $t$ 将产生该射线中的每个点 $P$。
请注意，对于 $t=0$，我们得到 $P=O$；对于 $t=1$，我们得到 $P=V$。 $t$ 的负值屈服点在相反的方向——即在相机后面。 因此，我们可以将参数空间分为三部分，如表 2-1 所示。 图 2-9 显示了参数空间的示意图。

Table2-1:	参数空间的细分
t < 0	摄像头后面[相机后面]
0 ≤ t ≤ 1	在相机和投影平面/视口之间
t > 1	在投影平面/视口前面

---

图 2-9：参数空间中的几个点

---

请注意，相交方程中没有任何内容表明球体必须在相机前面；
该方程将很自然地为相机后面的交叉点产生解决方案。
显然，这不是我们想要的，
所以我们应该忽略任何 $t<0$ 的解。
为了避免进一步的数学不愉快，我们将解限制为 $t>1$； 也就是说，我们将渲染超出投影平面的任何内容。

---

另一方面，我们不想给 $t$ 的值设置一个上限；
我们希望看到相机前面的所有物体，无论它们有多远。
然而，因为在后面的阶段我们会想要缩短射线，
我们现在将引入这种形式，并给 $t$ 一个上限值 $+\infty$（对于不能直接表示“无穷大”的语言，可以诡计一个非常大的数字）。

---

我们现在可以用一些伪代码来形式化我们迄今为止所做的一切。 作为一般规则，我们假设代码可以访问它需要的任何数据，因此我们不会费心明确地传递参数，例如画布，而是专注于真正必要的参数。

---

main 方法现在如示例2-2 所示。

O = (0, 0, 0)
for x = -Cw/2 to Cw/2 {
	for y = -Ch/2 to Ch/2 {
		D = CanvasToViewport(x, y)
		color = TraceRay(O, D, 1, inf)
		canvas.PutPixel(x, y, color)
	}
}

示例 2-2：main 方法

---

CanvasToViewport 函数非常简单，如示例2-3 所示。 常数 $d$ 表示相机与投影平面之间的距离。

CanvasToViewport(x, y) {
	return (x*Vw/Cw, y*Vh/Ch, d)
}

示例 2-3：CanvasToViewport 函数

---

TraceRay 方法（示例 2-4）计算光线与每个球体的交点，并返回在请求的 $t$ 范围内最近交点处球体的颜色。

TraceRay(O, D, t_min, t_max) {
	closest_t = inf
	closest_sphere = NULL
	for sphere in scene.spheres {
		t1, t2 = IntersectRaySphere(O, D, sphere)
		if t1 in [t_min, t_max] and t1 < closest_t {
			closest_t = t1
			closest_sphere = sphere
		}
		if t2 in [t_min, t_max] and t2 < closest_t {
			closest_t = t2
			closest_sphere = sphere
		}
	}
	if closest_sphere == NULL {
		❶ return BACKGROUND_COLOR
	}
	return closest_sphere.color
}

示例 2-4：TraceRay 方法

在示例 2-4 中，$O$ 表示射线的原点；
虽然我们正在追踪来自位于原点的相机的光线，但在后期阶段不一定会如此，因此它必须是一个参数。 这同样适用于 t_min 和 t_max。

请注意，当光线不与任何球体相交时，我们仍然需要返回一些颜色❶[代码中的❶]——在大多数示例中我选择了白色。return BACKGROUND_COLOR

---

最后，IntersectRaySphere（示例2-5）只是求解二次方程；

IntersectRaySphere(O, D, sphere) {
	r = sphere.radius
	CO = O - sphere.center
	a = dot(D, D)
	b = 2*dot(CO, D)
	c = dot(CO, CO) - r*r
	discriminant = b*b - 4*a*c
	if discriminant < 0 {
		return inf, inf
	}
	t1 = (-b + sqrt(discriminant)) / (2*a)
	t2 = (-b - sqrt(discriminant)) / (2*a)
	return t1, t2
}

示例 2-5：IntersectRaySphere 方法

---

为了将所有这些付诸实践，让我们定义一个非常简单的场景，如图 2-10 所示。

图 2-10：一个非常简单的场景，从上（左）和从右（右）看

---

在伪场景语言中，它是这样的：

viewport_size = 1 x 1
projection_plane_d = 1
sphere {
	center = (0, -1, 3)
	radius = 1
	color = (255, 0, 0) # Red
}
sphere {
	center = (2, 0, 4)
	radius = 1
	color = (0, 0, 255) # Blue
}
sphere {
	center = (-2, 0, 4)
	radius = 1
	color = (0, 255, 0) # Green
}

当我们在这个场景上运行我们的算法时，我们最终得到了一个非常棒的光线追踪场景（图 2-11）。

图 2-11：令人难以置信的光线追踪场景

您可以在以下位置找到该算法的实时实现：https://gabrielgambetta.com/cgfs/basic-rays-demo

我知道，这有点令人失望，不是吗？ 反射、阴影和抛光的外观在哪里？ 别担心，我们会到达那里的。 这是一个很好的第一步。 球体看起来像圆圈，这比看起来像猫要好。 它们看起来不太像球体的原因是我们缺少人类如何确定物体形状的关键组成部分：它与光相互作用的方式。 我们将在下一章中介绍。

---

六、概括

在本章中，我们奠定了光线追踪器的基础。 我们选择了固定设置（相机和视口的位置和方向，以及视口的大小）； 我们选择了球体和射线的表示； 我们已经探索了弄清楚球体和射线如何相互作用所必需的数学； 我们把所有这些放在一起，用纯色在画布上绘制球体。

下一章通过对光线与场景中物体相互作用的方式进行建模，更加详细地建立在此基础上。

---