LeetCode刷题------链表
目录
什么是链表
链表的类型
链表的存储方式
链表的定义
链表的操作
链表与数组的时间复杂度对比
LeetCode:203.移除链表元素
LeetCode:707.设计链表
LeetCode:206.反转链表
LeetCode:19.删除链表的倒数第N个节点
LeetCode:160. 相交链表
LeetCode:142.环形链表II
什么是链表
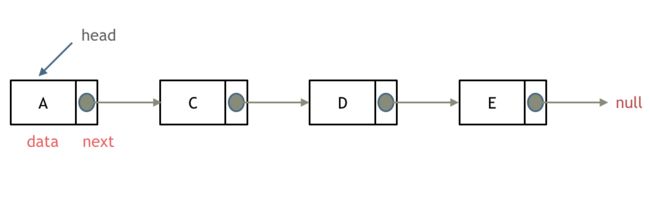
链表是一种通过指针串联在一起的线性结构,每一个节点由两部分组成,一个是数据域一个是指针域(存放指向下一个节点的指针),最后一个节点的指针域指向null(空指针的意思)。链表的入口节点称为链表的头结点也就是head。
链表的类型
1、单链表
单链表中的指针域只能指向节点的下一个节点。如上图
2、双链表
每一个节点有两个指针域,一个指向下一个节点,一个指向上一个节点。双链表既可以向前查询也可以向后查询。
![]()
3、循环链表
链表首尾相连。循环链表可以用来解决约瑟夫环问题。
![]()
链表的存储方式
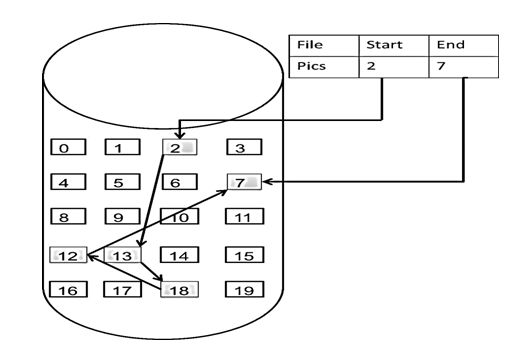
数组是在内存中是连续分布的,但是链表在内存中可不是连续分布的。链表是通过指针域的指针链接在内存中各个节点。所以链表中的节点在内存中不是连续分布的 ,而是散乱分布在内存中的某地址上,分配机制取决于操作系统的内存管理。
链表的定义
class LinkNode {
constructor(val, next) {
this.val = val;
this.next = next;
}
}链表的操作
1、删除节点
只要将C节点的next指针 指向E节点就可以了。那有同学说了,D节点不是依然存留在内存里么?只不过是没有在这个链表里而已。是这样的,所以在C++里最好是再手动释放这个D节点,释放这块内存。其他语言例如Java、Python、JavaScript,就有自己的内存回收机制,就不用自己手动释放了。
![]()
2、添加节点
链表的增添和删除都是O(1)操作,也不会影响到其他节点。但是要注意,要是删除第五个节点,需要从头节点查找到第四个节点通过next指针进行删除操作,查找的时间复杂度是O(n)。
![]()
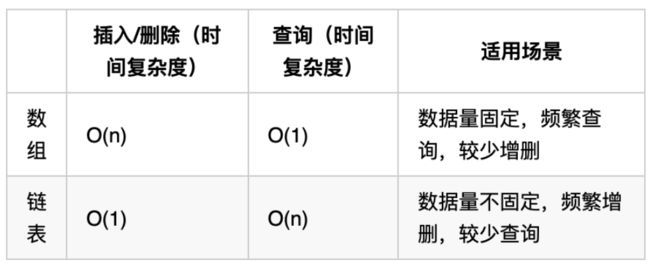
链表与数组的时间复杂度对比
数组在定义的时候,长度就是固定的,如果想改动数组的长度,就需要重新定义一个新的数组。
链表的长度可以是不固定的,并且可以动态增删, 适合数据量不固定,频繁增删,较少查询的场景。
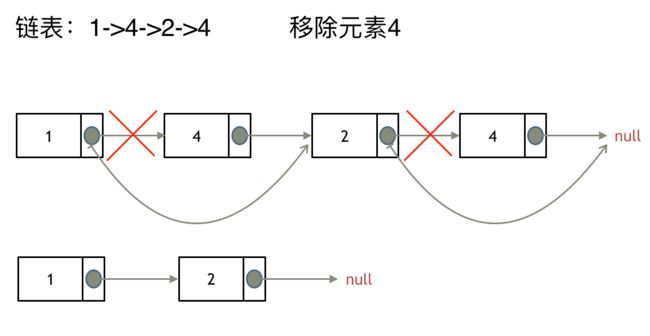
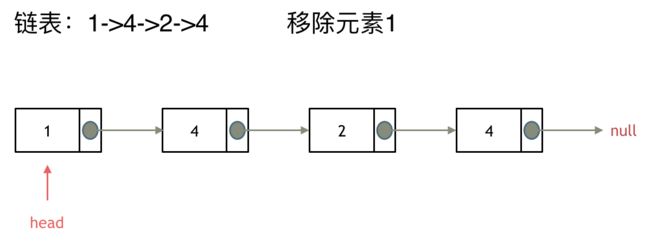
LeetCode:203.移除链表元素
链表操作中,可以使用原链表来直接进行删除操作,也可以设置一个虚拟头结点在进行删除操作,接下来看一看哪种方式更方便。
因为单链表的特殊性,只能指向下一个节点,刚刚删除的是链表的中第二个,和第四个节点,那么如果删除的是头结点又该怎么办呢?
这里就涉及如下链表操作的两种方式:
- 直接使用原来的链表来进行删除操作。
- 设置一个虚拟头结点在进行删除操作。
来看第一种操作:直接使用原来的链表来进行移除。
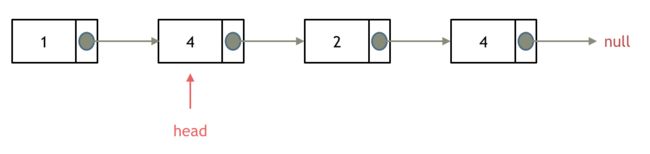
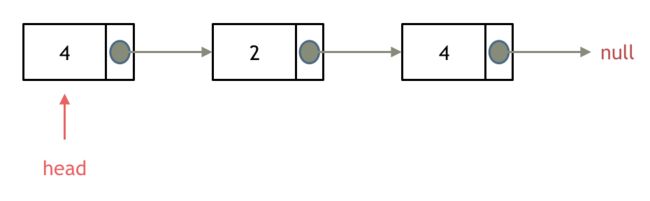
移除头结点和移除其他节点的操作是不一样的,因为链表的其他节点都是通过前一个节点来移除当前节点,而头结点没有前一个节点。所以头结点如何移除呢,其实只要将头结点向后移动一位就可以,这样就从链表中移除了一个头结点。c和c++别忘将原头结点从内存中删掉。
在单链表中移除头结点 和 移除其他节点的操作方式是不一样,其实在写代码的时候也会发现,需要单独写一段逻辑来处理移除头结点的情况。
以一种统一的逻辑来移除 链表的节点呢。其实可以设置一个虚拟头结点,这样原链表的所有节点就都可以按照统一的方式进行移除了。来看看如何设置一个虚拟头。c和c++别忘将原头结点从内存中删掉。最后呢在题目中,return 头结点的时候,别忘了 return dummyNode->next;, 这才是新的头结点。
![]()
//在原链表操作
var removeElements = function(head, val) {
const ret = new ListNode(0, head); //头节点
let cur = ret; //当前节点
while (cur.next) {
if (cur.next.val === val) {
cur.next = cur.next.next;
continue;
}
cur = cur.next;
}
return ret.next;
};LeetCode:707.设计链表
这道题目设计链表的五个接口:
- 获取链表第index个节点的数值
- 在链表的最前面插入一个节点
- 在链表的最后面插入一个节点
- 在链表第index个节点前面插入一个节点
- 删除链表的第index个节点
可以说这五个接口,已经覆盖了链表的常见操作,是练习链表操作非常好的一道题目.
//定义
class LinkNode {
constructor(val, next) {
this.val = val;
this.next = next;
}
}
/**
* Initialize your data structure here.
* 单链表 储存头尾节点 和 节点数量
*/
var MyLinkedList = function() {
this._size = 0;
this._tail = null;
this._head = null;
};
/**
* Get the value of the index-th node in the linked list. If the index is invalid, return -1.
* @param {number} index
* @return {number}
*/
MyLinkedList.prototype.getNode = function(index) {
if(index < 0 || index >= this._size) return null;
// 创建虚拟头节点
let cur = new LinkNode(0, this._head);
// 0 -> head
while(index-- >= 0) {
cur = cur.next;
}
return cur;
};
MyLinkedList.prototype.get = function(index) {
if(index < 0 || index >= this._size) return -1;
// 获取当前节点
return this.getNode(index).val;
};
/**
* Add a node of value val before the first element of the linked list. After the insertion, the new node will be the first node of the linked list.
* @param {number} val
* @return {void}
*/
MyLinkedList.prototype.addAtHead = function(val) {
const node = new LinkNode(val, this._head);
this._head = node;
this._size++;
if(!this._tail) {
this._tail = node;
}
};
/**
* Append a node of value val to the last element of the linked list.
* @param {number} val
* @return {void}
*/
MyLinkedList.prototype.addAtTail = function(val) {
const node = new LinkNode(val, null);
this._size++;
if(this._tail) {
this._tail.next = node;
this._tail = node;
return;
}
this._tail = node;
this._head = node;
};
/**
* Add a node of value val before the index-th node in the linked list. If index equals to the length of linked list, the node will be appended to the end of linked list. If index is greater than the length, the node will not be inserted.
* @param {number} index
* @param {number} val
* @return {void}
*/
MyLinkedList.prototype.addAtIndex = function(index, val) {
if(index > this._size) return;
if(index <= 0) {
this.addAtHead(val);
return;
}
if(index === this._size) {
this.addAtTail(val);
return;
}
// 获取目标节点的上一个的节点
const node = this.getNode(index - 1);
node.next = new LinkNode(val, node.next);
this._size++;
};
/**
* Delete the index-th node in the linked list, if the index is valid.
* @param {number} index
* @return {void}
*/
MyLinkedList.prototype.deleteAtIndex = function(index) {
if(index < 0 || index >= this._size) return;
if(index === 0) {
this._head = this._head.next;
// 如果删除的这个节点同时是尾节点,要处理尾节点
if(index === this._size - 1){
this._tail = this._head
}
this._size--;
return;
}
// 获取目标节点的上一个的节点
const node = this.getNode(index - 1);
node.next = node.next.next;
// 处理尾节点
if(index === this._size - 1) {
this._tail = node;
}
this._size--;
};LeetCode:206.反转链表
如果再定义一个新的链表,实现链表元素的反转,其实这是对内存空间的浪费。其实只需要改变链表的next指针的指向,直接将链表反转 ,而不用重新定义一个新的链表
![]()
首先定义一个cur指针,指向头结点,再定义一个pre指针,初始化为null。然后就要开始反转了,首先要把 cur->next 节点用tmp指针保存一下,也就是保存一下这个节点。为什么要保存一下这个节点呢,因为接下来要改变 cur->next 的指向了,将cur->next 指向pre ,此时已经反转了第一个节点了。接下来,就是循环走如下代码逻辑了,继续移动pre和cur指针。最后,cur 指针已经指向了null,循环结束,链表也反转完毕了。 此时我们return pre指针就可以了,pre指针就指向了新的头结点。
双指针方法:
var reverseList = function(head) {
if(!head || !head.next) return head;
let temp = null, pre = null, cur = head;
while(cur) {
temp = cur.next;
cur.next = pre;
pre = cur;
cur = temp;
}
// temp = cur = null;
return pre;
};<扩展>递归
递归法相对抽象一些,但是其实和双指针法是一样的逻辑,同样是当cur为空的时候循环结束,不断将cur指向pre的过程。关键是初始化的地方,可能有的同学会不理解, 可以看到双指针法中初始化 cur = head,pre = NULL,在递归法中可以从如下代码看出初始化的逻辑也是一样的,只不过写法变了。
// 递归:
var reverse = function(pre, head) {
if(!head) return pre;
const temp = head.next;
head.next = pre;
pre = head
return reverse(pre, temp);
}
var reverseList = function(head) {
return reverse(null, head);
};
// 递归2
var reverse = function(head) {
if(!head || !head.next) return head;
// 从后往前翻
const pre = reverse(head.next);
head.next = pre.next;
pre.next = head;
return head;
}
var reverseList = function(head) {
let cur = head;
while(cur && cur.next) {
cur = cur.next;
}
reverse(head);
return cur;
};<扩展>迭代
LeetCode:19.删除链表的倒数第N个节点
双指针的经典应用,如果要删除倒数第n个节点,让fast移动n步,然后让fast和slow同时移动,直到fast指向链表末尾。删掉slow所指向的节点就可以了。思路是这样的,但要注意一些细节。分为如下几步:
-
首先这里我推荐大家使用虚拟头结点,这样方便处理删除实际头结点的逻辑
-
fast首先走n + 1步 ,为什么是n+1呢,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作),如图:
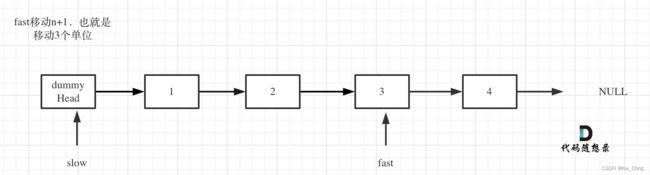
-
var removeNthFromEnd = function(head, n) { let ret = new ListNode(0, head), slow = fast = ret; while(n--) fast = fast.next; while (fast.next !== null) { fast = fast.next; slow = slow.next }; slow.next = slow.next.next; return ret.next; };
LeetCode:160. 相交链表
同:面试题 02.07. 链表相交 - 力扣(LeetCode)
简单来说,就是求两个链表交点节点的指针。 这里同学们要注意,交点不是数值相等,而是指针相等。看如下两个链表,目前curA指向链表A的头结点,curB指向链表B的头结点:
我们求出两个链表的长度,并求出两个链表长度的差值,然后让curA移动到,和curB 末尾对齐的位置,如图:.
此时我们就可以比较curA和curB是否相同,如果不相同,同时向后移动curA和curB,如果遇到curA == curB,则找到交点。否则循环退出返回空指针。
LeetCode:142.环形链表II
这道题目,不仅考察对链表的操作,而且还需要一些数学运算。主要考察两知识点:
- 判断链表是否环
- 如果有环,如何找到这个环的入口
判断链表是否有环
可以使用快慢指针法,分别定义 fast 和 slow 指针,从头结点出发,fast指针每次移动两个节点,slow指针每次移动一个节点,如果 fast 和 slow指针在途中相遇 ,说明这个链表有环。为什么fast 走两个节点,slow走一个节点,有环的话,一定会在环内相遇呢,而不是永远的错开呢。首先第一点:fast指针一定先进入环中,如果fast指针和slow指针相遇的话,一定是在环中相遇,这是毋庸置疑的。那么来看一下,为什么fast指针和slow指针一定会相遇呢?可以画一个环,然后让 fast指针在任意一个节点开始追赶slow指针。
![]()
fast和slow各自再走一步, fast和slow就相遇了。这是因为fast是走两步,slow是走一步,其实相对于slow来说,fast是一个节点一个节点的靠近slow的,所以fast一定可以和slow重合。
如果有环,如何找到这个环的入口?
此时已经可以判断链表是否有环了,那么接下来要找这个环的入口了。假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点 再到环形入口节点节点数为 z。
那么相遇时: slow指针走过的节点数为: x + y, fast指针走过的节点数:x + y + n (y + z),n为fast指针在环内走了n圈才遇到slow指针, (y+z)为 一圈内节点的个数A。因为fast指针是一步走两个节点,slow指针一步走一个节点, 所以 fast指针走过的节点数 = slow指针走过的节点数 * 2:(x + y) * 2 = x + y + n (y + z)两边消掉一个(x+y): x + y = n (y + z)。因为要找环形的入口,那么要求的是x,因为x表示 头结点到 环形入口节点的的距离。所以要求x ,将x单独放在左面:x = n (y + z) - y ,再从n(y+z)中提出一个 (y+z)来,整理公式之后为如下公式:x = (n - 1) (y + z) + z 注意这里n一定是大于等于1的,因为 fast指针至少要多走一圈才能相遇slow指针。这个公式说明什么呢?先拿n为1的情况来举例,意味着fast指针在环形里转了一圈之后,就遇到了 slow指针了。当 n为1的时候,公式就化解为 x = z,这就意味着,从头结点出发一个指针,从相遇节点 也出发一个指针,这两个指针每次只走一个节点, 那么当这两个指针相遇的时候就是 环形入口的节点。也就是在相遇节点处,定义一个指针index1,在头结点处定一个指针index2。让index1和index2同时移动,每次移动一个节点, 那么他们相遇的地方就是 环形入口的节点。
那么 n如果大于1是什么情况呢,就是fast指针在环形转n圈之后才遇到 slow指针。其实这种情况和n为1的时候 效果是一样的,一样可以通过这个方法找到 环形的入口节点,只不过,index1 指针在环里 多转了(n-1)圈,然后再遇到index2,相遇点依然是环形的入口节点。
// 先判断是否是环形链表
var detectCycle = function(head) {
if(!head || !head.next) return null;
let slow =head.next, fast = head.next.next;
while(fast && fast.next && fast!== slow) {
slow = slow.next;
fast = fast.next.next;
}
if(!fast || !fast.next ) return null;
slow = head;
while (fast !== slow) {
slow = slow.next;
fast = fast.next;
}
return slow;
};
var detectCycle = function(head) {
if(!head || !head.next) return null;
let slow =head.next, fast = head.next.next;
while(fast && fast.next) {
slow = slow.next;
fast = fast.next.next;
if(fast == slow) {
slow = head;
while (fast !== slow) {
slow = slow.next;
fast = fast.next;
}
return slow;
}
}
return null;
};==============双指针解决链表问题===============
21. 合并两个有序链表 - 力扣(LeetCode)
var mergeTwoLists = function(list1, list2) {
const prehead = new ListNode(-1);
let prev = prehead;
while (list1 !== null && list2 !== null) {
if (list1.val < list2.val) {
prev.next = list1;
list1 = list1.next;
} else {
prev.next = list2;
list2 = list2.next;
}
prev = prev.next;
}
if (list1 === null) {
prev.next = list2;
} else {
prev.next = list1;
}
return prehead.next;
};86. 分隔链表 - 力扣(LeetCode)
思路:将原链表看成2份,一个存储比x大或等于的元素,一个存储比x小的元素,最后合并两个链表
var partition = function(head, x) {
// 记录比x大的链表,虚拟头结点
let dummy1 = new ListNode(-1);
// 记录比x小的链表,虚拟头结点
let dummy2 = new ListNode(-1);
// p1,p2分别是两个链表的头指针
let p1 = dummy1, p2 = dummy2;
// 原链表的头指针
let p = head;
while(p){
if (p.val >= x) {
p1.next = p;
p1 = p1.next;
} else {
p2.next = p;
p2 = p2.next;
}
// 断开原链表中每个节点的next
let temp = p.next;
p.next = null;
p = temp;
}
p2.next = dummy1.next;
return dummy2.next;
};