论文笔记 :Geometric Reasoning for Single Image Structure Recovery David(Orientation Map算法)(CVPR 2009)
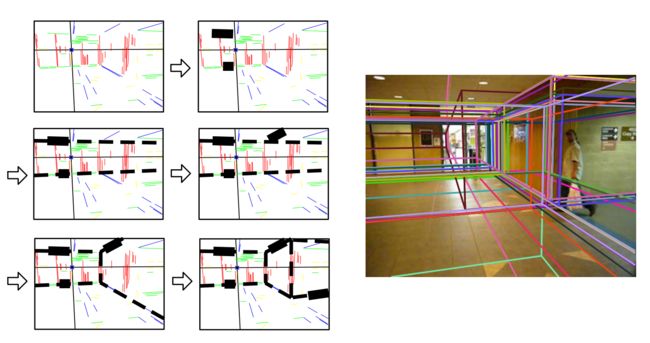
恢复室内布局,传统方法主要分为3个步骤:线段检测和估计消失点、生成布局假设、对假设进行打分,方向图可以作为布局打分重要部分。

墙角分为3类:
凸角convex(+)corners.
凹角concave(-)corners.
遮挡角occluding(>)corners.
所有房间布局可由这3种基本类别进行组合。
进一步根据消失点划分3个区域(视角不同),每个区域只有凸角、凹角、遮挡角1、遮挡角2,这4种类型的墙角
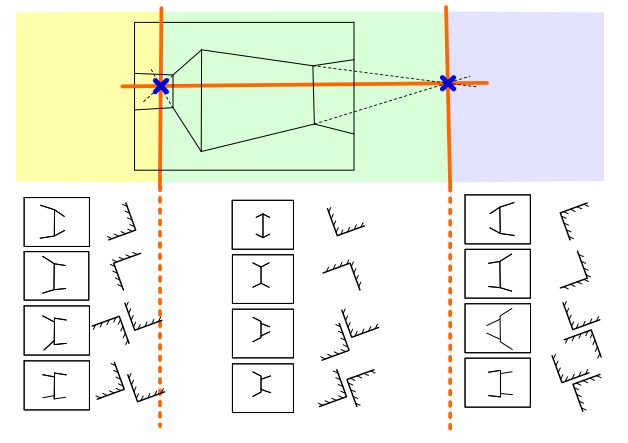
所以在进行线段检测和消失点估计后,先寻找一对平行线段(在3D空间,在透视图中是交于同一消失点的线段),判断其所在区域,检测对是否存在其区域中的4种类墙角。

约束: 对于4种类型的交,各自最少需要检测到3、3、4、4条线段才能确定
Generating Building Hypotheses
- 估计消失点时已经将线段分为3类,代表3个方向上的线段。
- 检测1对直线 l i l_{i} li 和 l j l_{j} lj, l i l_{i} li位于视野水平线上方(天花板墙线) 和 l j l_{j} lj位于视野水平线下方(地板墙线),且 l i l_{i} li 和 l j l_{j} lj相交,因为透视图中平行线相交。将线段加入,初始0个墙角的布局 H 0 H_{0} H0中
- 假设布局有k个角 H k H_{k} Hk,k从1开始,从线段集合中选择可以和 H k − 1 H_{k-1} Hk−1中组成墙角的线段,依据上面提到的约束,将新布局更新到 H k H_{k} Hk。
最后得到布局集合: H ← H 0 ∪ H 1 ∪ ⋯ ∪ H n H \leftarrow H_{0} \cup H_{1} \cup \cdots \cup H_{n} H←H0∪H1∪⋯∪Hn

Evaluating Building Hypotheses(orientation map)
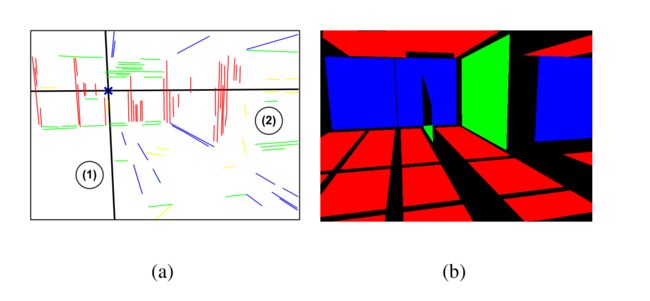
一个点如果由2个不同方向的线段支持,比如上图(1)中的点,由2个方向(绿、蓝)支持,所以(1)中的点的方向垂直于绿、蓝。
(2)中的点,由2个方向(红、绿)支持,所以(2)中的点的方向垂直于红、绿线。上下的蓝线被绿线阻挡,绿线。右边的蓝线被红线阻挡,所以不能作为(2)中点的支持方向。
区域扫描(sweep)过程:
比如有在x方向的线段集合: L x = { l x , 1 , l x , 2 , ⋯ , l x , n x } L_{x}=\left\{l_{x, 1}, l_{x, 2}, \cdots, l_{x, n_{x}}\right\} Lx={lx,1,lx,2,⋯,lx,nx},其中 x ∈ { 1 , 2 , 3 } x \in\{1,2,3\} x∈{1,2,3}表示3个方向。
定义: S ( l x , i , v y , α ) S\left(l_{x, i}, v_{y}, \alpha\right) S(lx,i,vy,α),表示从x方向的第i条线段 l x , i l_{x, i} lx,i朝着消失点y前进 α \alpha α得到的凸多边形,其中线段 l x , i l_{x, i} lx,i所在消失点方向和扫描方向垂直,如下图
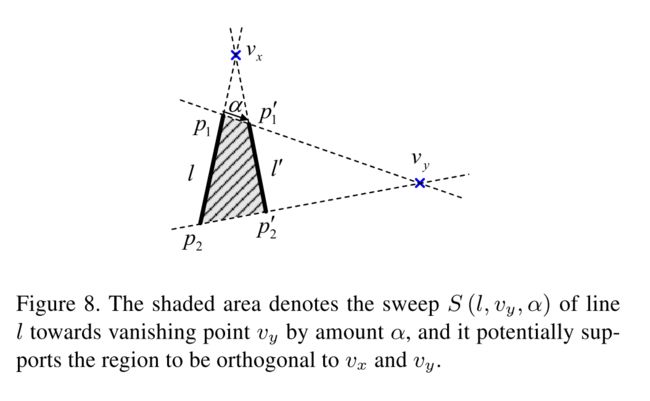
线段 l l l的消失点为x方向,扫描方向为y方向,它们是垂直关系( x ≠ y , x ≠ z , y ≠ z x \neq y, x \neq z, y \neq z x=y,x=z,y=z), S ( l , v y , α ) S\left(l, v_{y}, \alpha\right) S(l,vy,α)由4个点组成,分别是线段 l l l的端点 p 1 , p 2 p_{1}, p_{2} p1,p2, p 1 ′ , p_{1}^{\prime}, p1′, 和 p 2 ′ p_{2}^{\prime} p2′通过
p 1 ′ = p 1 + α ( v y − p 1 ) p 2 ′ = i n t e r s e c t i o n ( line ( v x , p 1 ′ ) , line ( v y , p 2 ) ) p_{1}^{\prime}=p_{1}+\alpha\left(v_{y}-p_{1}\right)\\ p_{2}^{\prime}=i n t e r s e c t i o n\left(\operatorname{line}\left(v_{x}, p_{1}^{\prime}\right), \operatorname{line}\left(v_{y}, p_{2}\right)\right) p1′=p1+α(vy−p1)p2′=intersection(line(vx,p1′),line(vy,p2))
扫描过程直到遇到垂直于x和y方向平面的线段停止。扫描有分向前量 α ^ x , i \widehat{\alpha}_{x, i} α x,i和向后量 − β ^ x , i -\widehat{\beta}_{x, i} −β x,i,都最大化它们:
α ^ x , i = max ( α ) , β ^ x , i = max ( β ) \widehat{\alpha}_{x, i}=\max (\alpha), \widehat{\beta}_{x, i}=\max (\beta) α x,i=max(α),β x,i=max(β)
所以有 S ( l x , i , v y , α ) S\left(l_{x, i}, v_{y}, \alpha\right) S(lx,i,vy,α)和 S ( l x , i , v y , − β ) S\left(l_{x, i}, v_{y},-\beta\right) S(lx,i,vy,−β),其中 α ≥ 0 , β ≥ 0 \alpha \geq 0, \beta \geq 0 α≥0,β≥0,不会和z方向上的线段 L z L_{z} Lz有交点。
一个像素集合,表示的是 x x x方向上线段集合 L x L_{x} Lx,朝向消失点 y y y,方向为 z z z,如下描述:
P x , y , z = ⋃ l x , i ∈ L x S ( l x , i , v y , α ^ x , i ) ∪ S ( l x , i , v y , β ^ x , i ) P_{x, y, z}=\bigcup_{l_{x, i} \in L_{x}} S\left(l_{x, i}, v_{y}, \widehat{\alpha}_{x, i}\right) \cup S\left(l_{x, i}, v_{y}, \widehat{\beta}_{x, i}\right) Px,y,z=lx,i∈Lx⋃S(lx,i,vy,α x,i)∪S(lx,i,vy,β x,i)
为了确保map的唯一性和准确性,同一平面上,比如xy平面朝着2个消失点方向x和y都能得到对应扫描区域,都表示该区域方向为z,取交集:
R z = P x , y , z ∩ P y , x , z R_{z}=P_{x, y, z} \cap P_{y, x, z} Rz=Px,y,z∩Py,x,z
为了确保方向唯一性,只有唯一属于一个方向的扫描区域可以接受:
O z = R z ∩ R x c ∩ R y c O_{z}=R_{z} \cap R_{x}^{c} \cap R_{y}^{c} Oz=Rz∩Rxc∩Ryc
下图显示了 O 1 , O 2 , O 3 O_{1}, O_{2}, O_{3} O1,O2,O3