C++算法：有向无环图拓扑排序（领接链表）

---

前言

前文有向无环图实现游戏技能树中我们使用了矩阵存储图的关系，可以称之为邻接矩阵。显然，链表也是可以实现的。在图结构入门一文中，我们也提到了链表存储的原理。本文我们就以链表形式来完成这一结构，并进行拓扑排序。

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、邻接表

我们还是使用前文中的同一张图结构。

说是以链表形式存储，但顶点我们显然还是可以用一个数组来存储更方便，数组的下标即是顶点编号。那么数组相应下标中就可以用来存储本顶点的邻接表的第一个元素。实际就是一个数组中的链表。在C++中就是list adj[n];，这里n表示顶点总数。

二、代码

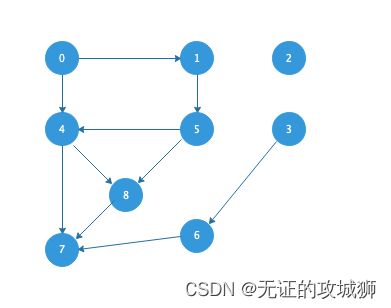
当然，如果list adj[n];这么写看着不舒服，也可以写成vector> adj; 使用向量更直观一点，虽然理论上使用原生数组会略微快一点。实际使用如果顶点数量不多，应该没多大差距。图的邻接关系我们继续沿用前文的int arr[11][2] = {{0,1},{0,4},{1,5},{5,4},{4,7},{4,8},{3,6},{6,7},{8,7},{5,8},{2}};

1、生成图

代码如下（示例）：

#include 
#include 
#include 
#include 

using namespace std;

class Graph{
    private:
        int vertex, idx=0; //顶点数、顶点下标 
        int* visited;    //存储是否已访问
        int* indegree;   //存储入度
        int* outdegree;  //存储出度
        list<int>* adj;  //存储邻接链表

    public:
        Graph(const int n, int arr[][2]){
            vertex = n;
            adj = new list<int>[vertex];          //这是数组中的链表
            visited = new int[vertex];                     
            indegree = new int[vertex];          
            outdegree = new int[vertex];
            for (int i=0; i<11; i++){               //生成邻接表
                adj[arr[i][0]].push_back(arr[i][1]);
            }
            adj[2].remove(0);    //补最后一个{2}的问题，默认会认成{2,0}
            find_indegree();
            find_outdegree();
        }
        ~Graph(){
            delete[] toposort;
            delete[] outdegree;
            delete[] indegree;
            delete[] visited;
            delete[] adj;
        }

这一部分与前文差大的差别就在于，没有了矩阵matrix，替换成了adj这个存储list的数组，以及生成邻接关系的代码，这里采用了adj[arr[i][0]].push_back(arr[i][1]);其实就是一个list。我们往数组相应下标（表示了顶点编号）的list中，添加此下标代表的顶点所连接到的顶点编号。这里要是理解不能的话，去看前文图结构入门中的存储原理图。
其余数组变量与前文是基本一样的，笔者这里也是代码复用了一波~

2、出度、入度计算

在拓扑排序前要先计算各顶点的出度和入度。在构造函数中，已经有了调用函数：

        void find_indegree(){
            for (int i=0; i<vertex; i++){
                for (auto v: adj[i]){
                    indegree[v]++;
                }
            }
        }

        void find_outdegree(){
            for (int i=0; i<vertex; i++){
                outdegree[i] = adj[i].size();
            }
        }

这里的计算方法和邻接矩阵不同，入度计算我们要去数组中找每个list是否有此顶点，有就代表被连接了。所以我们去统计每个list中所有顶点出现多少次即可。
出度计算就更容易了，直接去对应数组下标，此list的长度就是出度，代表此顶点连接了几个顶点。

3、拓扑排序

前文也演示了一种用深度优先搜索的拓扑排序方法，这里肯定不能再用同样的方法了。我们换成前面提到过的，从出度为0的顶点开始，每找到一个0出度的顶点，我们就将它剔除，并将与此顶点相连的所有顶点出度减一。循环操作，即可完成拓扑排序。
代码如下（示例）：

        int* toposort = new int[9];   //生成排序完成存储的数组
        stack<int> s;    //栈用来倒顶点顺序
        queue<int> q;    //队列用来存储过程顶点
        void topo(){     //第一次搜索没有出度的顶点
            for (int i=0; i<vertex; ++i){
                if (outdegree[i]==0){
                    q.push(i);    //入队
                }
            }
            for (int i=0; i<vertex; ++i){   //循环搜索没有出度的顶点
                int tmp = q.front();  
                s.push(tmp);      //入栈
                q.pop();          //出队
                outdegree[tmp] = -1;   //用-1定义已访问
                for (int j=0; j<vertex; ++j){
                    for (int v : adj[j]){        //数组中的list中搜索
                        if (v == tmp){          //如果搜索到已剔除的顶点
                            outdegree[j]--;     //当前下标表示的顶点出度减1
                            if (outdegree[j] == 0){
                                q.push(j);      //减1后如果没有出度了，就入队
                            }
                        }
                    }
                }
            }
            while (s.size()){   //从栈中倒出到结果数组
                int tmp = s.top();
                s.pop();
                toposort[idx++] = tmp;
            }
        }

上面代码就是拓扑排序的过程，这就要比矩阵深度搜索的方法复杂得多了。笔者详细注释了代码的运行逻辑。总体思想就是：

• 第一步先将所有没有出度的顶点压入队列中。
• 第二次循环开始时，将前面队列中的顶点先取一个到栈中，相应的顶点出队。
• 将这个被出队的顶点，表示为已排序。如果在链表中找到这个顶点，那么将连接到这个顶点的所有顶点的出度减1。
• 如果减1出度后的顶点的没有出度了，那就把这顶点也压入队中。
• 循环完成后，如果图结构中没有环，栈中就存储了所有顶点，将栈倒出即完成拓扑排序。

以上代码没有判断图是否有环，如果要加入判断。只需在出队前判断队列是否为空if q.empty(); 如果队列是空的就表示图中有环路。即使是子图存在环路也一样可以检测到。

---

总结

笔者在代码中也偷懒了不少地方，比如节点数，输入数据arr的长度有些地方直接写成数字了，当然这并不影响阅读与代码的运行。最后测试的结果与前文的排序结果是不一样的：

int main(){
    int arr[11][2] = {{0,1},{0,4},{1,5},{5,4},{4,7},{4,8},{3,6},{6,7},{8,7},{5,8},{2}};
    Graph t(9,arr);
    t.topo();
    for (int i=0; i<9; i++){
        cout << t.toposort[i] << " ";
    }

}
//0 1 5 4 3 8 6 7 2     排序结果

为了测试方便，直接将 toposort 数组写在 public 中了。这种拓扑排序的结果如图：

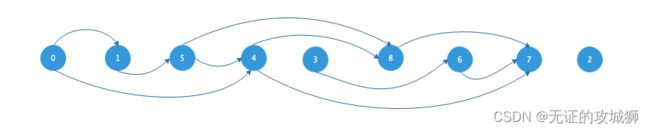
拓扑排序在实际应用中，除了前文简单实现的游戏技能树外，还常用于工程中计划管理中，因为工程计划是有依赖关系的。比如在软件工程中，就可以用有向无环图表示源代码文件之间的依赖关系。