深度学习笔记之Transformer(二)关于注意力分数的总结

引言

上一节介绍了注意力机制的基本逻辑。本节作为过渡文章，归纳注意力分数这个概念。

回顾：$\text{Nadaraya-Watson}$核回归

作为一种懒惰学习$(\text{Lazy Learnging})$方法，$\text{Nadaraya-Watson}$核回归基于训练集$\mathcal{D}=\{(x^{(i)},y^{(i)}){\}}_{i=1}^N$，关于陌生样本$x$的预测过程表示为：
f ( x ) = [ κ ( x , x ( 1 ) ) ∑ j = 1 N κ ( x , x ( j ) ) , κ ( x , x ( 2 ) ) ∑ j = 1 N κ ( x , x ( j ) ) , ⋯   , κ ( x , x ( N ) ) ∑ j = 1 N κ ( x , x ( j ) ) ] 1 × N ( y ( 1 ) y ( 2 ) ⋮ y ( N ) ) N × 1 = ∑ i = 1 N κ ( x , x ( i ) ) ∑ j = 1 N κ ( x , x ( j ) ) ⋅ y ( i ) \begin{aligned} f(x) & = \left[\frac{\kappa(x,x^{(1)})}{\sum_{j=1}^N \kappa(x,x^{(j)})},\frac{\kappa(x,x^{(2)})}{\sum_{j=1}^N \kappa(x,x^{(j)})},\cdots,\frac{\kappa(x,x^{(N)})}{\sum_{j=1}^N \kappa(x,x^{(j)})}\right]_{1 \times N} \begin{pmatrix} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(N)} \end{pmatrix}_{N \times 1} \\ & = \sum_{i=1}^N \frac{\kappa(x,x^{(i)})}{\sum_{j=1}^N \kappa(x,x^{(j)})} \cdot y^{(i)} \end{aligned} f(x)​=[∑j=1N​κ(x,x(j))κ(x,x(1))​,∑j=1N​κ(x,x(j))κ(x,x(2))​,⋯,∑j=1N​κ(x,x(j))κ(x,x(N))​]1×N​ ​y(1)y(2)⋮y(N)​ ​N×1​=i=1∑N​∑j=1N​κ(x,x(j))κ(x,x(i))​⋅y(i)​
在训练集$\mathcal{D}$给定的条件下，已知一个未知样本$x$，那么${\sum }_{j=1}^N\kappa (x,x^{(j)})$必然是一个确定的值。因而导致$y^{(i)}$的系数$\begin{array}{r}\frac{\kappa (x,x^{(i)})}{{\sum }_{j=1}^N\kappa (x,x^{(j)})}\end{array}$必然仅与$x,x^{(i)}$相关，而与其他训练样本无关。这里将其简写为如下形式：
$$f(x)=\sum _{i=1}^N\alpha (x,x^{(i)})\cdot y^{(i)}$$
而$\alpha (x,x^{(i)})$这个函数结果可被称作$x$关于训练样本$x^{(i)}$的注意力权重$(\text{Attention Weight})$；假设$\kappa (x,x^{(i)})$描述的是径向基核函数$(\text{Radial Basis Function,RBF})$，可以将$f(x)$表示成如下形式：
$$\{\begin{array}{l}\begin{array}{rl}\kappa (x,x^{(i)})& =\exp \left\{-\frac{1}{2{\sigma }^2}||x-x^{(j)}|{|}^2\right\}\\ f(x)& =\sum _{i=1}^N\frac{\kappa (x,x^{(i)})}{{\sum }_{j=1}^N\kappa (x,x^{(j)})}\cdot y^{(i)}\\ & =\sum _{i=1}^N\text{Softmax}\left[-\frac{1}{2{\sigma }^2}||x-x^{(i)}|{|}^2\right]\cdot y^{(i)}\end{array}\end{array}$$
此时再去观察$\begin{array}{r}\alpha (x,x^{(i)})=\text{Softmax}\left[\frac{1}{2{\sigma }^2}||x-x^{(i)}|{|}^2\right]\end{array}$，可以发现：$\text{Softmax}$函数仅仅是一个归一化操作——该函数自身并不包含注意力信息。而真正包含注意力信息的只有$\begin{array}{r}-\frac{1}{2{\sigma }^2}||x-x^{(i)}|{|}^2\end{array}$。我们将这部分函数的结果称作注意力分数$(\text{Attention Score})$。
很明显，注意力分数是指没有被‘标准化’$(\text{Normalization})$的;描述样本/向量间的‘纯粹的信息’。

使用流程图来描述上述过程：

再回首：$\text{Seq2seq}$中的注意力机制

回过头观察$\text{Seq2seq}$：$\text{Seq2seq}$中的注意力机制是否也满足上述流程$?$

场景构建：

• 在$\text{Seq2seq}$中，编码器中各时刻的序列信息$\left[h_{\mathcal{L};j},h_{\mathcal{R};(\mathcal{T}+1-j)}\right](j=1,2,\cdots ,\mathcal{T})$视作$\text{Keys}$，而对应的$\text{Values}$就是它们自身；

• 在解码器中某一时刻$t(t\in \{1,2,\cdots ,{\mathcal{T}}^{\prime }\})$的序列信息$h_{\mathcal{D}}^{(t)}$(也可以是上一时刻的$h_{\mathcal{D}}^{(t-1)}$，这里用$h_{\mathcal{D}}^{(t)}$示例)视作$\text{Query}$；
  将$h_{\mathcal{D}}^{(t)}$作为$\text{Query}$的动机在于：我们主观想要了解$h_{\mathcal{D}}^{(t)}$与各$\left[h_{\mathcal{L};j},h_{\mathcal{R};(\mathcal{T}+1-j)}\right](j=1,2,\cdots ,\mathcal{T})$之间的相关性信息。因而$h_{\mathcal{D}}^{(t)}$是‘刻意信息’，而$\left[h_{\mathcal{L};j},h_{\mathcal{R};(\mathcal{T}+1-j)}\right](j=1,2,\cdots ,\mathcal{T})$是句子自身性质产生的‘无意信息’。

  关于‘刻意信息’与‘无意信息’详见上一节注意力机制基本介绍

执行过程：
详细执行过程见深度学习笔记之$\text{Seq2seq}$——注意力机制的执行过程

• 通过构建神经网络的方式对$\text{Query}$和$\text{Keys}$进行计算，得到注意力分数${\mathcal{E}}_t$：
  $$\{\begin{array}{l}{\mathcal{H}}_{Bi}={\left\{[h_{\mathcal{L};j},h_{\mathcal{R};(\mathcal{T}+1-j)}{]}_{j=1}^{\mathcal{T}}\right\}}_{\mathcal{T}\times 1}^T\\ \\ {\mathcal{O}}_t={\mathcal{W}}_{\text{Attn}}\cdot \left[\text{Concat}\left(h_{\mathcal{D}}^{(t)},{\mathcal{H}}_{Bi}\right)\right]+b_{\text{Attn}}\\ {\mathcal{O}}_t=\text{Tanh}({\mathcal{O}}_t)\\ {\mathcal{E}}_t={\mathcal{V}}^T{\mathcal{O}}_t\end{array}$$
• 使用$\text{Softmax}$函数对注意力分数${\mathcal{E}}_t$进行标准化，得到各时刻的注意力权重$(\text{Attention Weights})$：
  $${\mathcal{S}}_t=\text{Softmax}({\mathcal{E}}_t)\Rightarrow {\mathcal{S}}_t=(s_{t1},s_{s2},\cdots ,s_{t\mathcal{T}}{)}_{\mathcal{T}\times 1}^T$$
• 将注意力权重与编码器各时刻序列信息(此时将其视作$\text{Values}$)执行内积操作，得到该时刻的$\text{Context}$向量${\mathcal{C}}_t$：
  $$\begin{array}{rl}{\mathcal{C}}_t& =[{\mathcal{S}}_t{]}^T{\mathcal{H}}_{Bi}\\ & =\sum _{j=1}^{\mathcal{T}}{s}_{tj}\cdot [h_{\mathcal{L};j},h_{\mathcal{R};(\mathcal{T}+1-j)}]\end{array}$$

流程角度观察完全相同。只不过这里的$\text{Keys,Values}$是相同信息。

注意力机制的泛化表示

将查询向量$\mathcal{Q}$，$\mathcal{M}$个键值对$\{({\mathcal{K}}_j,{\mathcal{V}}_j){\}}_{j=1}^{\mathcal{M}}$映射到高维空间中：
$$\{\begin{array}{l}\mathcal{Q}\in {\mathbb{R}}^q\\ {\mathcal{K}}_j\in {\mathbb{R}}^k\\ {\mathcal{V}}_j\in {\mathbb{R}}^v\end{array}$$
对应的注意力输出可表示为：
f [ Q , ( K 1 , V 1 ) , ( K 2 , V 2 ) , ⋯   , ( K M , V M ) ⏟ M 个 ] = ∑ j = 1 M α ( Q , K j ) V j f \left[\mathcal Q,\underbrace{(\mathcal K_1,\mathcal V_1),(\mathcal K_2,\mathcal V_2),\cdots,(\mathcal K_{\mathcal M},\mathcal V_{\mathcal M})}_{\mathcal M个}\right] = \sum_{j=1}^{\mathcal M} \alpha(\mathcal Q,\mathcal K_j) \mathcal V_j f ​Q,M个 (K1​,V1​),(K2​,V2​),⋯,(KM​,VM​)​​ ​=j=1∑M​α(Q,Kj​)Vj​
其中$\alpha (\mathcal{Q},{\mathcal{K}}_j)$表示注意力权重：
这仅是$\mathcal{Q}$与编号为$j$的$\text{Keys}$的注意力权重，它的结果是一个标量;基于$\text{Softmax}$函数范围内的标量$\Rightarrow \alpha (\mathcal{Q},{\mathcal{K}}_j)\in \mathbb{R}$
$$\begin{array}{rl}\alpha (\mathcal{Q},{\mathcal{K}}_j)& =\text{Softmax}\left[a(\mathcal{Q},{\mathcal{K}}_j)\right]\\ & =\frac{\exp \left[a(\mathcal{Q},{\mathcal{K}}_j)\right]}{{\sum }_{i=1}^{\mathcal{M}}\exp \left[a(\mathcal{Q},{\mathcal{K}}_j)\right]}\end{array}$$
同上，对应的$a(\mathcal{Q},{\mathcal{K}}_j)$仅表示$\mathcal{Q}$与编号为$j$的$\text{Keys}$的注意力分数。与注意力权重相同，它的结果同样是一个标量。$\text{Softmax}$函数仅作为归一化作用，不改变数据格式：
$$a(\mathcal{Q},{\mathcal{K}}_j)\in \mathbb{R}$$

加性注意力机制

将注意力分数展开，可以得到如下形式：
$$a(\mathcal{Q},{\mathcal{K}}_j)={\mathcal{V}}_j^T\cdot \text{Tanh}({\mathcal{W}}_{\mathcal{K};j}\cdot {\mathcal{K}}_j+{\mathcal{W}}_{\mathcal{Q}}\cdot \mathcal{Q})$$
对应神经网络结构表示如下：

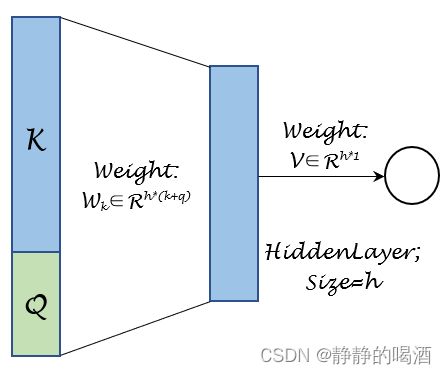
当然，这仅仅是一项——${\mathcal{K}}_j$与$\mathcal{Q}$的注意力分数。那么$\mathcal{M}$个注意力分数并行计算，它的注意力分数表示为：

• 这里的${\mathcal{W}}_{\mathcal{K}},{\mathcal{W}}_{\mathcal{Q}}$做了分开表示:使用不同权重矩阵单独对$\mathcal{K},\mathcal{Q}$进行训练，并将各自神经元的输出分布对应元素相加;
• 更常见的像$\text{Seq2seq}$中的表示方式：将$\mathcal{K},\mathcal{Q}$拼接起来(上图)，使用一个权重矩阵$\mathcal{W}$进行表示。这两种操作是等价的。
  $$a(\mathcal{Q},\mathcal{K})={\mathcal{V}}^T\cdot \text{Tanh}({\mathcal{W}}_{\mathcal{K}}\cdot \mathcal{K}+{\mathcal{W}}_{\mathcal{Q}}\cdot \mathcal{Q})$$

这种注意力机制的优势在于：即便${\mathcal{K}}_j$与$\mathcal{Q}$的大小(维数)不相同，并不影响注意力分数的计算。

缩放点积注意力机制

如果查询向量$\mathcal{Q}$与${\mathcal{K}}_j(j=1,2,\cdots ,\mathcal{M})$的大小(维数)相同：
这里的$d$表示$\mathcal{Q},{\mathcal{K}}_j$的向量维数。
$$\mathcal{Q},{\mathcal{K}}_j\in {\mathbb{R}}^d$$
那么可以使用缩放点积注意力机制$(\text{Scaled Dot-Product Attention})$对注意力分数进行如下计算：
$$a(\mathcal{Q},{\mathcal{K}}_j)=\frac{⟨\mathcal{Q},{\mathcal{K}}_j⟩}{\sqrt{d}}$$
其中$⟨\mathcal{Q},{\mathcal{K}}_j⟩$表示向量$\mathcal{Q},{\mathcal{K}}_j$的内积。而除以$\sqrt{d}$的操作的解释是：注意力分数结果对参数不是非常敏感。

关于这个解释，$d$是$\mathcal{Q},{\mathcal{K}}_j$向量的维数，而向量内的信息除以$\sqrt{d}$，只能想到它将注意力分数的解空间进行了一定程度的压缩/约束(正常情况下，$\sqrt{d}\ge 1$，是不小的。谁闲着没事将一个很小的特征向量做这种注意力的复杂操作，不怕模型过拟合吗~)
\quad
如果有更好的解释方式，欢迎小伙伴评论区讨论。

在基于$\text{Seq2seq}$注意力机制的动机中，我们介绍过内积求解注意力分数，它存在自身的优势：相比于加性注意力机制中神经网络产生的抽象特征，内积操作本身就有物理意义：描述向量$\mathcal{Q},{\mathcal{K}}_j$之间的相似度。
即便$\mathcal{Q},{\mathcal{K}}_j$大小不同，实际上依然不影响其执行内积操作。仅需要对其中一个向量乘以一个权重矩阵，使其拉成相同长度并执行内积，后续对该权重矩阵中的参数进行学习即可。这里并没有深挖关于该方向的信息，欢迎小伙伴交流讨论。

上述依然仅是单个向量$\mathcal{Q},{\mathcal{K}}_j$的注意力分数，那么多个$\text{Query,Keys}$可以得到一个矩阵：

场景构建：

• 查询向量$\mathcal{Q}$内包含$N$个$d$维向量：$\mathcal{Q}\in {\mathbb{R}}^{N\times d}$；
  查询向量也可以是多个。
• 键值对中的$\text{Keys}$内依然包含$\mathcal{M}$个向量信息：$\mathcal{K}\in {\mathbb{R}}^{\mathcal{M}\times d}$；
• 键值对中的$\text{Values}$内包含与$\text{Keys}$相同数量的向量信息：$\mathcal{V}\in {\mathbb{R}}^{\mathcal{M}\times v}$
  上面提到：$\mathcal{K},\mathcal{V}$有可能相同，也有可能不同。这里描述的是‘不同’的情况。

对应的注意力分数表示如下：
其中注意力分数$a(\mathcal{Q},\mathcal{K})$所描述的$N\times \mathcal{M}$矩阵中，每一个元素均是$\mathcal{Q}$中某向量于$\mathcal{K}$中某向量的内积$($相似性$)$结果。
$$a(\mathcal{Q},\mathcal{K})={\left[\frac{\mathcal{Q}{\mathcal{K}}^T}{\sqrt{d}}\right]}_{N\times \mathcal{M}}$$
对应的注意力池化过程表示如下：
这里的$\text{Softmax}$是对$a(\mathcal{Q},\mathcal{K})$中各行$N\times 1$元素做归一化。
$$f={\left\{\text{Softmax}[a(\mathcal{Q},\mathcal{K})]\right\}}_{N\times \mathcal{M}}\cdot {\mathcal{V}}_{\mathcal{M}\times v}f\in {\mathbb{R}}^{N\times v}$$

下一节将介绍自注意力机制$(\text{Self-Attention})$。

相关参考：
注意力分数【动手学深度学习v2】