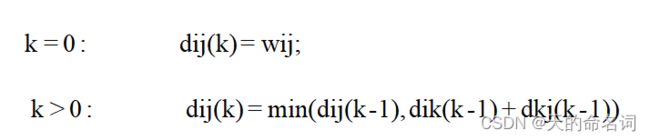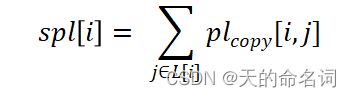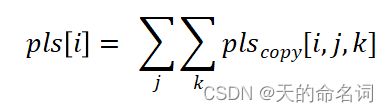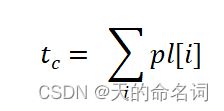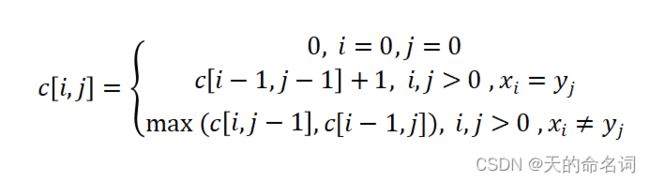天的命名词

【算法分析与设计报告】快递终端送货配送系统、基因序列比较、地图染色、文章查重系统、果园篱笆问题（附源码）

一、快递终端送货分配问题

问题描述

假设某快递终端投递站，服务n个小区，小区与快递点之间有道路相连，如下图，边上的权值表示距离。

图1-1 小区快递点图

现在设有m包裹，每个包裹都有自己的目的地及总量。

假设送货员一次投递的最大重量无限，设计一个把所有货物送到目的的最短路径算法。
现在设一个快递员一次投递的最大重量为100kg（包裹的总重量远大于100kg), 设计一个把所有货物送到目的的跑的趟数最小的算法。
设从投递点出发，投递第k包裹的总路径长度为pl，其投递代价为,plXw[k]，设计一个把所有货物送到目的的代价最小的算法。
快递员行驶速度为10km/h,快递员在一个小区的投放时间为10分钟，设计一个把所有货物送到目的的时间最少最小的算法。
你还可以提出什么问题？如何解决该问题？

1.1 问题一

1.1.1 问题一解决问题所用方法及基本思路

将第一题抽象就是在一张无向图中，找到一棵最小生成树。但是，仅仅是本问题也不仅仅是最小生成树问题，还需考虑以下问题：

(1)可以多次走过同一个点以获得更短路径。及在比较路程更短的情况下，快递员可以先回到上一小区，再前往下一小区。

(2)一次不一定能够遍历全部顶点，需要向回走。快递员需延边，一个小区一小区走。经过反复分析，多源最短路Floyd算法可以完美解决以上问题。

Floyd算法为对加权连通图求多源最短路径，其是一种动态规划算法，稠密图效果最佳，甚至可以对有向图进行运算。其可以生成distance（距离矩阵）与path数组，第一个存放了点和点之间最短路径值，第二个存放了计算所需的中间点。

Floyd算法的基本思想非常简单，可以简单的理解成一个循环插点的过程。首先明确我们的目标是寻找从点 i 到点 j 的最短路径。而从任意节点 i 到任意节点 j 的最短路径不外乎2种可能：一是直接从 i 到j，二是从 i 经过若干个节点 k 到 j 。所以，我们假设 distance(i,j) 为节点 i 到节点 j 的最短路径的距离，然后依次插入节点 k ，我们检查 distance(i,k) + distance(k,j) < distance(i,j) 是否成立，如果成立，证明从 i 到 k 再到 j 的路径比i直接到 j 的路径短，我们便令distance(i,j) = distance(i,k) + distance(k,j)，这样一来，当遍历完所有节点 k ，distance(i,j)中记录的便是 i 到 j 的最短路径的距离。其状态转移方程为：

1.1.2 算法描述

伪代码描述：
Floyd（graph）
//实现Flody算法
//输入：不包含长度为负的回路的图的权重矩阵graph
//输出：包含最短路径长度的距离矩阵distance;
for k ← 0 to n
  for i ← 0 to m
  for j ← 0 to p
   d[i][j] = min(d[i][j],d[i][k]+d[k][j])
retrun d

1.1.3 算法的时间空间复杂度分析

该算法的基本运算为比较，即在每次递归找出最短的路径，递归公式为：

时间复杂度为：O(n3),时间复杂度比较高，不适合计算大量数据。

空间复杂度为：O(n2)。

由于三重循环结构紧凑，对于稠密图，效率要高于执行 n 次dijkstra算法。

1.1.4 算法实例

输入：

图1-2 快递终端送货分配系统问题一输入

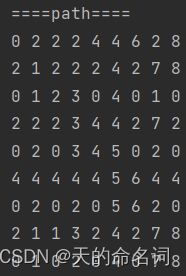
输出：

图1-3 快递终端送货分配系统问题一输出

1.1.5 代码


public class Floyd {
    public static int[][] distance;  // 距离矩阵
    public static int[][] path;     // 路径矩阵

    public static void floyd(int[][] graph) {
        //初始化距离矩阵 distance
        distance = graph;
        //初始化路径
        path = new int[graph.length][graph.length];
        for (int i = 0; i < graph.length; i++) {
            for (int j = 0; j < graph[i].length; j++) {
                path[i][j] = j;
            }
        }
        //开始 Floyd 算法
        //每个点为中转
        for (int i = 0; i < graph.length; i++) {
            //所有入度
            for (int j = 0; j < graph.length; j++) {
                //所有出度
                for (int k = 0; k < graph[j].length; k++) {
                    //以每个点为「中转」，刷新所有出度和入度之间的距离
                    //例如 AB + BC < AC 就刷新距离
                    if (graph[j][i] != -1 && graph[i][k] != -1) {
                        int newDistance = graph[j][i] + graph[i][k];
                        if (newDistance < graph[j][k] || graph[j][k] == -1) {
                            //刷新距离
                            graph[j][k] = newDistance;
                            //刷新路径
                            path[j][k] = i;
                        }
                    }
                }
            }
        }
    }

    public static int Way(int startIndex){
        boolean[] tags = new boolean[distance.length];
        for (int i = 0; i < tags.length; i++){
            tags[i] = false;
        }
        tags[startIndex] = true;
        return SeekDistance(startIndex, tags, startIndex);
    }

    public static int SeekDistance(int startIndex, boolean[] tags, int Start){
        System.out.print("->" + startIndex + "\t");
        int l = 0;
        // NoAccess数组记录未访问的index 如NoAccess[0] = 5 5号还未访问
        int[] NoAccess = new int[distance.length];
        for (int i = 0; i < distance.length; i++){
            NoAccess[i] = -1;
        }
        int j = 0;
        for (int i = 0; i < distance.length; i++){
            if (!tags[i]) {
                NoAccess[j++] = i;
            }
        }

        // 遍历快递站与其他点的距离，找最小距离点
        int newIndex = foundmin(startIndex, tags);
        // 判断是否还能前进 当前道路已经尽头，结束。 加上 结束点到起点距离
        if (newIndex == -1){
            return distance[startIndex][Start];
        }
        // judgeChange(newIndex, startIndex)为中转点 或 -1
        if (judgeChange(newIndex, startIndex) != -1){
            l += distance[startIndex][judgeChange(newIndex, startIndex)] + distance[judgeChange(newIndex, startIndex)][newIndex];
        }else {
            l += distance[startIndex][newIndex];
        }
        tags[newIndex] = true;
        l = l + SeekDistance(newIndex, tags, Start);
        return l;
    }

    /*
        查找最近未配送点下标
        index 第几行
        newIndex 在index行中最小下标值 若无可前进点返回-1
     */
    public static int foundmin(int index, boolean[] tags){
        int min = Integer.MAX_VALUE;
        int newIndex = -1;
        for (int i = 0; i < distance[index].length; i++){
            if ((distance[index][i] < min) && !tags[i]) {
                min = distance[index][i];
                newIndex = i;
            }
        }
        return newIndex;
    }

    /*
        判断是否更改过 path (1)两点不相邻，显然不存在  (2) 找到了更小通路 且 此通路经过了那个点
        若有最小通路，则输出下标，否则就-1
     */
    public static int judgeChange(int newIndex, int startIndex){
        if (path[startIndex][newIndex] != newIndex) return path[startIndex][newIndex];
        return -1;
    }


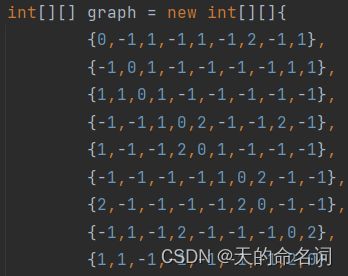
    public static void main(String[] args) {
        int[][] graph = new int[][]{
                {0,-1,1,-1,1,-1,2,-1,1},
                {-1,0,1,-1,-1,-1,-1,1,1},
                {1,1,0,1,-1,-1,-1,-1,-1},
                {-1,-1,1,0,2,-1,-1,2,-1},
                {1,-1,-1,2,0,1,-1,-1,-1},
                {-1,-1,-1,-1,1,0,2,-1,-1},
                {2,-1,-1,-1,-1,2,0,-1,-1},
                {-1,1,-1,2,-1,-1,-1,0,2},
                {1,1,-1,-1,-1,-1,-1,2,0}
//                {0,6,3,-1,-1,7},
//                {6,0,4,2,5,-1},
//                {3,4,0,3,-1,8},
//                {-1,2,3,0,2,-1},
//                {-1,5,-1,2,0,-1},
//                {7,-1,8,-1,-1,0}
        };

        floyd(graph);

        System.out.println("====distance====");
        for (int[] ints : distance) {
            for (int anInt : ints) {
                System.out.print(anInt + " ");
            }
            System.out.println();
        }
        System.out.println("====path====");
        for (int[] ints : path) {
            for (int anInt : ints) {
                System.out.print(anInt + " ");
            }
            System.out.println();
         }

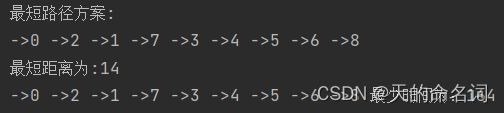
        System.out.println("最短路径方案:");
        System.out.println("\n最短距离为:" + Way(0));

    }
}

1.2 问题二

1.2.1 解决问题所用的方法及基本思路

针对第二问，给定了每次最多装100kg的物品，设计把所有货物送到目的的跑的趟数最小的算法。抽象出来就是一个0-1背包问题，其物品重量就是物品本身的重量，背包容量就是100kg，物品价值定义为单位“1”。简单来说，本问题就是如果让能装100kg的背包一次性装最多的物品。多次利用0-1背包问题即可完成该问题。

利用回溯法试设计一个算法求出0-1背包问题的解，也就是求出一个解向量。

在递归函数Backtrack中，

当i>n时，算法搜索至叶子结点，得到一个新的物品装包方案。此时算法适时更新当前的最优价值。

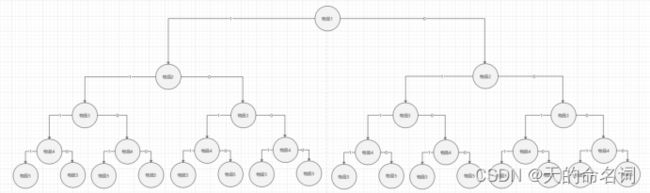
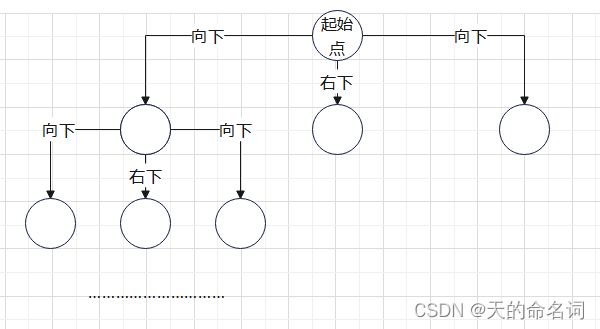
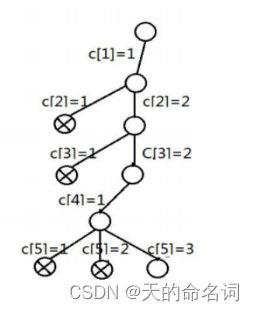
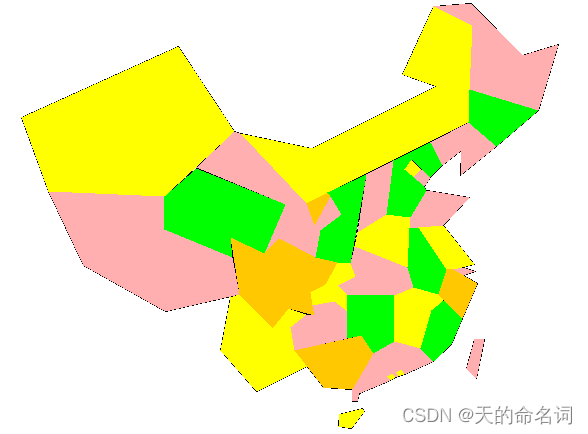
当i

设：

take[1..n] 其中take[i] = 1，代表第i个物品要放

take[i] = 0，代表第i个物品不放

约束条件：

第i个物品确定放置方法后，背包所剩重量足够放第i个物品

curW + w[i] <= bagV

(curW为当前背包重量，w[i]为第i个物品重量，bagV为背包总重)

求最优值回溯。

图1-4快递终端送货分配系统问题二状态树

1.2.2 算法描述

Backtrack(i,n,w[1..n],v[1..n],curW,curV)
// 回溯求01背包问题
// 输入：从第i个物品开始 
        w[i] 第i个物品重量 bastChoice[i]是否选择第i个物品
        v[i] 第i个物品价值 take[i]是否选择第i个物品
        curW 当前背包重量   curV 当前背包价值
        bagV 背包总重量 		n 为物品数
// 输出：改变bastChoic，选择物品
if i > n bestChoice ← take
	else
		for i ← j to 2 do
          take[i] ← j
          if curW + w[i] <= bagV
           curW ← curW + w[i]
           curV ← curV + v[i]
           Backtrack(i+1)
           curW ← curW - w[i]
           curV ← curV - v[i]

1.2.3 算法的时间空间复杂度分析

基本运算：比较

计算上界Bound()函数需要O(n)时间，在最坏的情况下有O(2n)个右子节点需要计算上界。分析问题可以发现，该回溯问题就是遍历了一颗二叉树，因此其算法复杂度就为O(2n)。

时间复杂度为：O(2n),时间复杂度比较高，不适合计算大量数据。

空间复杂度为：O(n)。

1.2.4算法实例

输入：

图1-5快递终端送货分配系统问题二输入

输出：

图1-6 快递终端送货分配系统问题二输出

1.2.5 代码

import java.util.Arrays;

public class Knapsack {

    public static int[] w = { 0, 20, 30, 30, 30, 40, 50, 50, 70};
    public static int[] v = { 0, 1, 1, 1, 1, 1, 1, 1, 1};
    public static int[] take;
    public static int[] bestChoice;
    public static int curV = 0;
    public static int curW = 0;
    public static int bestV = 0;
    public static int bagV = 100;

    public static void main(String[] args) {
        int Train = 0;
        bestChoice = new int[w.length];
        take = new int[w.length];
        int [] select;

        System.out.println(Arrays.toString(w));

        while (true){
            init();
            Knapsack(0);
            Train++;
            System.out.print("第" + Train + "趟送货," + "本趟送\t");
            for (int i = 1; i < w.length; i++){
                if (bestChoice[i] == 1 && w[i] != Integer.MAX_VALUE){
                    System.out.printf(i + "小区\t");
                }
            }
            System.out.println(Arrays.toString(bestChoice));

            // 对已经送过的地区将其w变为max_value
            // 记录是否已经全遍历
            int sum = 0;
            for (int i = 1; i < w.length; i++){
                if (bestChoice[i] == 1){
                    v[i] = 0;
                }
                sum += v[i];
            }
            if (sum == 0){
                break;
            }
        }
    }


    public static void init(){
        curV = 0;
        curW = 0;
        bestV = 0;
        bagV = 100;

    }
    public static void Knapsack(int i) {
        // 结束条件

        if (i > w.length - 1) {

            // 判断前一个V是否大于bestV 转移take[]数组存储的选择情况
            if (curV > bestV) {
                bestV = curV;
                for (int j = 0; j < take.length; j++) {
                    bestChoice[j] = take[j];
                }
            }
        } else {
            // 先都不放入背包，递归至底层，在从最后一个选择开始
            // 遍历当前节点（物品）的子节点：0 不放入背包 1：放入背包
            for (int j = 0; j < 2; j++) {
                take[i] = j;
                if (j==0) {
                    //不放入背包，接着往下走
                    Knapsack(i + 1);
                } else {
                    //约束
                    if (curW + w[i] <= bagV) {
                        //更新当前重量和价值
                        curW += w[i];
                        curV += v[i];
                        //继续向下深入
                        Knapsack(i + 1);
                        // 当从上一行代码maxV出来后，需要回溯容量和值
                        curW -= w[i];
                        curV -= v[i];
                    }
                }
            }
        }
    }

1.3问题三

1.3.1解决问题所用的方法及基本思路

设从投递点出发，投递第i包裹的总路径长度为l(i)。此题可以转换为求最小生成树，在求快递路径。使用Dijkstra算法较为简便。Dijkstra算法算是贪心思想实现的，首先把起点到所有点的距离存下来找个最短的，然后松弛一次再找出最短的，所谓的松弛操作就是，遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近，如果更近了就更新距离，这样把所有的点找遍之后就存下了起点到其他所有点的最短距离。

算法的思路：

Dijkstra算法采用的是一种贪心的策略，声明一个数组result来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合：初始时，原点i的路径权重被赋为 0（result[i] = 0）。若对于顶点i存在能直接到达的边，则把result[i]设为其距离,同时把所有其他（i不能直接到达的）顶点的路径长度设为无穷大（-1）。

从result数组选择最小值，则该值就是源点s到该值对应的顶点的最短路径，并且把该点加入然后，新加入的顶点是否可以到达其他顶点并且通过该顶点到达其他点的路径长度是否比源点直接到达短，如果是，那么就替换这些顶点在result中的值。

1.3.2解决问题所用的方法及基本思路

1.3.3算法的时间空间复杂度分析

基本运算：比较

时间复杂度为：O(n^2)。

空间复杂度为：O(n)。

该算法用了两层for，外层为需要访问的顶点个数，时间复杂度为O(n)，内层有两个for，第一个for为挑选未被访问的顶点的最短距离，时间复杂度为O(n)，第二个for为在与选中顶点有直接路径的顶点中对比距离是否需要更新，时间复杂度为O(n)，所以总的时间复杂度为O(n2)。

1.3.4算法实例

输入：

图1-7 快递终端送货分配系统问题三输入

输出：

图1-8 快递终端送货分配系统问题三输出

1.3.5 代码

import java.util.ArrayList;

public class Dijkstra {

    public static void main(String[] args) {
        //地图的邻接矩阵
        int[][] graph = {{0,-1,1,-1,1,-1,2,-1,1},
                {-1,0,1,-1,-1,-1,-1,1,1},
                {1,1,0,1,-1,-1,-1,-1,-1},
                {-1,-1,1,0,2,-1,-1,2,-1},
                {1,-1,-1,2,0,1,-1,-1,-1},
                {-1,-1,-1,-1,1,0,2,-1,-1},
                {2,-1,-1,-1,-1,2,0,-1,-1},
                {-1,1,-1,2,-1,-1,-1,0,2},
                {1,1,-1,-1,-1,-1,-1,2,0}};

        //每个小区所需的重量
        int[] w = {20, 30, 30, 30, 40, 50, 50, 70};

        for (int i = 0; i < graph.length - 1; i++) {
            int end = i+1;
            System.out.println("第0个节点到第" + end +"个节点的路径总长度为：" + getShortestPaths(graph, 0, end));
            System.out.println("其投递代价为：" + getShortestPaths(graph, 0, i + 1) * w[i]);

        }
    }


    public static int getShortestPaths(int[][] graph, int src, int des) {
        int[] result = new int[graph.length]; // 用于存放节点src到其它节点的最短距离
        boolean[] notFound = new boolean[graph.length]; // 用于判断节点是否被遍历
        ArrayList path = new ArrayList(); // 用于存放(src, des)之间的最短路径

        // step1：初始化，将src节点设置为已经访问，并且初始化该节点到其他所有节点之间的距离
        notFound[src] = true;
        path.add(src);

        for (int i = 0; i < graph.length; i++) {
            result[i] = graph[src][i];
        }
        while (true) {
            // step2：找到剩余未访问的节点中，距离src最近的一个节点，作为curNode
            int curNode = getNearestNode(graph, notFound, result);
            // step3：更新所有节点距离src节点的最短距离（需要考虑curNode）
            update(graph, curNode, notFound, result, path);
            if (curNode == des) {
                break;
            }
        }

        return result[des];
    }
    // 找到剩余未访问的节点中，距离源节点最近的一个节点编号
    public static int getNearestNode(int[][] graph, boolean[] notFound, int[] result) {
        int minIndex = -1;
        int minLength = Integer.MAX_VALUE;
        for (int i = 0; i < graph.length; i++) {
            if (!notFound[i] && result[i] != -1 && result[i] < minLength) {
                minIndex = i;
                minLength = result[i];
            }
        }

        return minIndex;
    }
    // 更新与curNode节点直接相连接的未被访问的节点距离
    public static void update(int[][] graph, int curNode, boolean[] notFound, int[] result, ArrayList path) {
        notFound[curNode] = true;
        path.add(curNode);

        for (int j = 0; j < graph.length; j++) {
            // 节点j未访问过 && 节点curNode与节点j之间需要直接相连
            if (!notFound[j] && graph[curNode][j] != -1) {
                // 更新result[j]
                if (result[j] > result[curNode] + graph[curNode][j] || result[j] == -1) {
                    result[j] = result[curNode] + graph[curNode][j];
                }
            }
        }
    }

}

1.4问题四

1.4.1解决问题所用的方法及基本思路

时间和路程问题抽象出来其实是等价的，路程越短，所花的时间也就越短，因此可以继续沿用第一问的思路，使用Floyd算法即可。

1.4.2算法描述

同理第一问

1.4.3算法的时间空间复杂度分析

该算法的基本运算为比较，即在每次递归找出最短的路径，递归公式为：

k = 0: dij(k) = wij;

k > 0: dij(k) = min(dij(k-1),dik(k-1)+dkj(k-1))

时间复杂度为：O(n3)。

空间复杂度为：O(n2)。

1.4.4算法实例

输入：

图1-9 快递终端送货分配系统问题四输入

输出：

图1-10 快递终端送货分配系统问题四输出

1.5提出的问题及解决方法

提出问题：如果需要选择一个地点作为快递枢纽，可以选择在哪？

解决方法：首先，选址的找到一个最有的排列组合，可以通过万能钥匙的遗传算法求解。然后需求分配则需要按照最小费用最大流问题的思路进行分配。最小费用最大流问题指的是，在一个由一个源和汇和中间节点构成的配送网络中，每个路径都有其成本权重和流量约束，在满足流量约束的条件下找到最小配送成本的配送路径，这种方法就称为最小费用最大流方法。借鉴了这种方法之后，再根据模型的约束进行改进，得到一个新的最小费用最大流方法。

本问题可以使用粒子群算法妥善求解，粒子群算法是近年来发展起来的一种新的进化算法，它是从初始解出发，通过迭代寻找最优解，通过适应度来评价解的品质，通过追随当前搜索到的最优值来寻找全局最优。在每一次迭代中，粒子通过跟踪两个“极值”来更新自己的位置：一个是个体最优解pbest，是每个粒子自身所找到的最优解，另一个极值是群体最优解gbest，是整个群体目前找到的最优解。这种算法具有容易实现、精度高、收敛快等优点。

二、文章查重系统

2.1 问题描述

(1）段落抄袭
设段落单篇文章抄袭阈值 pt =10%，待检测文章的与其他单篇文章任一段落最长公共子序列长度大于 pt 算作抄袭。例如，假如待检测文章第 i 段落有1000字，与其他第 j 篇单篇文章第 k 段落最长公共子序长度为100，则该段落算作抄袭，抄袭长度定义为 plp[i,j,k ]。则待检测文章第 i 段与其他第 j 篇文章抄袭长度定义:

设待检测文章第 i 段的抄袭文章的集合为， L[i]

段落抄袭长度：

(2）连续句子抄袭：
设连续句子抄袭率 psth =13，以段落记，待检测文章第 i 段落，与其他单篇文章第 j 段落连续字符超过13个字符的算作句子抄袭。抄袭长度记为：＝连续字符的个数，其中 k 为该段落的第 k 个抄袭的句子。段落句子
抄袭长度

(3）段落综合抄袭长度：

(4）文章总的抄袭长度:

(5）文章总的抄袭率 :

要求：
1．下载或者制作至少10篇有抄袭的文章

2．任选一篇文章，计算出该文章的抄袭率，若该文章抄袭率超过10%，显示出该文章的抄袭段落。
3．在抄袭段落中用红色标出段落抄袭，用黄色标出句子抄袭。

4．用鼠标单击标出抄袭的部分，要显示被抄袭文章的标题，及抄袭的段落，并标出抄袭的部分。

5．你认为该问题抄袭率定义是否有问题，若有请指出，并论述其原因。
6．文档要求给出重要算法的算法设计的基本方法（分治，动态规划等），选用这些设计方法的原因，给出该算法的伪代码，分析该算法的时间复杂度，
给出算法实际运行的结果。

1.2 解决问题所用的方法及基本思路

基本思路：

动态规划求解两字符串的最长公共子序列
蛮力法求解最长公共连续子序列
类的封装及组合

实现过程：

定义了两个类(Chapter、checkRepeat)、一个控制模块control、一个界面模块mian。

Chapther类中考虑到题目要求最小单位到句，故使用二维指针数组形式来存放组织一篇文章，使用一位指针数组形式来存放段落句子数。

文章的基本属性：文章标题（string title）、文章（vector> chapter）、文章段落数（int paragraph_num）、段落句子数（vector sentence_num）、文章总字数(int sum_char)、文章序号（int ID = count）

1、定义Chapter.h接口如下：

#pragma once
#include 
#include 
#include 
using namespace std;
class Chapter
{
private:
    //文章标题
    string title;
    vector> chapter;
    int paragraph_num;
    vector sentence_num;
    //记录文章个数
    static int count;
    int ID = count;
    //文章总字符数
    int sum_char;
public:
    Chapter();
    ~Chapter();
    int howID() { return ID; };
    string* random_str(const int len);
    int get_paragraph_num();
    int get_sentence_num(int paragraph);
    int get_str_num();
    void set_paragraph_num(const int n);
    void set_sentence_num(const int n);
    //获取文章一段,返回对应段落的指针
    string* get_paragraph(Chapter chapter, int paragragh);
    //获取文章一句,返回对应句子的指针
    string* get_sentence(Chapter chapter, int paragragh, int sentence);
    void display();
};

检查器checkRepeat的基本属性：

2、定义checkRepeat接口

#pragma once
#include "chapter.h"
#include 
struct Paragraph_Sentence
{
	int sum_paragraph;
	vector sum_sentence;
};
class checkRepeat
{
public:
	checkRepeat();
	checkRepeat(Chapter& cha, vector& lib);
	~checkRepeat();
	//段落抄袭查重
	int** paragraph_check();
	//连续句子抄袭查重
	int** sentence_check();
	//段落综合抄袭长度
	int paragraph_repeat(int paragraph);
	//文章抄袭总长度
	int sum_repeat();
	//文中总抄袭率
	double repeat_rate();
	//get/set函数
	int** get_pl();
	int** get_pls();
	double get_pt() { return pt; };
	int get_psth() { return psth; };
	void set_chapter(Chapter& cha);
	void set_library(vector& lib) { library = lib; };
private:
	Paragraph_Sentence paragraph_sentence;
	//单篇文章抄袭阈值10%
	const float pt = 0.1f;
	//连续句子抄袭率13
	const int psth = 13;
	int** pl;
	int** pls;
	//进行查重的文章
	Chapter chapter;
	//参照文章库
	vector library;
	//求最长公共子序列O(n*2^m)->O(m*n)
	int LCS(const string s1, const string s2);
	//求最长公共连续子序列O(n^3)->O(m*n),但是小规模的解可能不包含再更大规模的问题中,故不能采用动态规划
	int RecursionLCS(const string str1, const string str2);
};

3、LCS函数的动态规划思路

规律分析：

设X=，Y=为两个序列，Z=是他们的任意公共子序列

经过分析：

1、如果xm = yn，则zk = xm = yn 且 Zk-1是Xm-1和Yn-1的一个LCS

2、如果xm != yn 且 zk != xm，则Z是Xm-1和Y的一个LCS

3、如果xm != yn 且 zk != yn，则Z是X和Yn-1的一个LCS

所以如果用一个二维数组c表示字符串X和Y中对应的前i，前j个字符的LCS的长度话，可以得到以下公式：

求ABCBDAB和BDCABA的LCS如下图所示：

4、RecursionLCS函数的双循环思路

第一重循环确定第一个字符串的对齐位置，第二重循环确定第二个字符串的对齐位置，每次循环确定一组两个字符串的对齐位置，并从此对齐位置开始匹配两个字符串的最长子串，如果匹配到的最长子串比已知的（由前面的匹配过程找到的）最长子串长，则更新已知最长子串的内容。

使用两重循环进行字符串的对齐匹配过程如下图所示：

1.3 采用数据结构描述

二维指针数组——文章的句子
一维指针数组——段落的句子数
二维数组——LCS的备忘录、查重操作后的数据记录等
串——句子

1.4 算法描述

LCS（X，Y）
输入：字符串X，Y
输出：输出X、Y的最长公共子序列数
m ← X.length
n ← Y.length
let b[1…m,1…n] be new tables
for i ← 0 to m
	c[i,0] ← 0
for j = 0 to n
	c[j,0] ← 0
for	 i ← 1 to m
	for j = 1 to n
		if 
			c[i,j] ← c[i-1,j-1] + 1
		elseif
			c[i,j] ← max(c[i-1,j],c[i,j-1])
return c[m-1,n-1]

RecursionLCS(X，Y)
输入：字符串X，Y
输出：输出X、Y的最长公共子序列数
m ← X.length
n ← Y.length
ans_lstr ← 0
for i ← 0 to m
	for j ← 0 to n
		lstr ← 0
		if  continue
		str1 ← , str2 ← 
		for k ← 0 to min(x.length, y.length)
			if  
				lstr++
			elseif
				break
		ans_lstr ← man(ans_lstr, lstr)
return ans_lstr

1.5 算法时间空间复杂度分析

LCS：

基本运算：比较

执行次数：m*n

渐进表示：O（m*n）

RecursionLCS：

基本运算：比较

执行次数：m*n ～ n^3

渐进表示：O（m*n）

1.6 代码

#pragma once
#include 
#include 
#include 
using namespace std;

class Chapter
{
private:
    //文章标题
    string title;
    vector> chapter;
    int paragraph_num;
    vector sentence_num;
    //记录文章个数
    static int count;
    int ID = count;
    //文章总字符数
    int sum_char;
public:
    Chapter();
    ~Chapter();
    int howID() { return ID; };
    string* random_str(const int len);
    int get_paragraph_num();
    int get_sentence_num(int paragraph);
    int get_str_num();
    void set_paragraph_num(const int n);
    void set_sentence_num(const int n);
    //获取文章一段,返回对应段落的指针
    string* get_paragraph(Chapter chapter, int paragragh);
    //获取文章一句,返回对应句子的指针
    string* get_sentence(Chapter chapter, int paragragh, int sentence);
    void display();
};

#pragma once
#include "chapter.h"
#include 
struct Paragraph_Sentence
{
	int sum_paragraph;
	vector sum_sentence;
};
class checkRepeat
{
public:
	checkRepeat();
	checkRepeat(Chapter& cha, vector& lib);
	~checkRepeat();

	//段落抄袭查重
	int** paragraph_check();
	//连续句子抄袭查重
	int** sentence_check();
	//段落综合抄袭长度
	int paragraph_repeat(int paragraph);
	//文章抄袭总长度
	int sum_repeat();
	//文中总抄袭率
	double repeat_rate();
	//get/set函数
	int** get_pl();
	int** get_pls();
	double get_pt() { return pt; };
	int get_psth() { return psth; };
	void set_chapter(Chapter& cha);
	void set_library(vector& lib) { library = lib; };
private:
	Paragraph_Sentence paragraph_sentence;
	//单篇文章抄袭阈值10%
	const float pt = 0.1f;
	//连续句子抄袭率13
	const int psth = 13;
	int** pl;
	int** pls;
	//进行查重的文章
	Chapter chapter;
	//参照文章库
	vector library;
	//求最长公共子序列O(n*2^m)->O(m*n)
	int LCS(const string s1, const string s2);
	//求最长公共连续子序列O(n^3)->O(m*n),但是小规模的解可能不包含再更大规模的问题中,故不能采用动态规划
	int RecursionLCS(const string str1, const string str2);
};

#include "chapter.h"

//默认构造函数：生成段落随机（3-9段）,句子数随机（3-10句），句子所含字母随机（20-100）
Chapter::Chapter()
{
    count++;
    srand((unsigned)time(NULL));
    int paragraph_num = rand() % 6 + 3;
    int sentence_num = rand() % 7 + 3;
    int str_num = rand() % 81 + 20;
    //段落随机（3-8段）
    set_paragraph_num(paragraph_num);
    //句子数随机（3-9句）
    for (int i = 0; i < get_paragraph_num(); i++)
    {
        set_sentence_num(sentence_num);
    }
    chapter.resize(get_paragraph_num());
    //初始化文章
    for (int i = 0; i < get_paragraph_num(); i++)
    {
        chapter[i].resize(get_sentence_num(i));
        for (int j = 0; j < get_sentence_num(i); j++)
        {
            //句子所含字母随机（20-100）
            chapter[i][j] = random_str(str_num);
        }
    }
    //计算字符个数
    sum_char = paragraph_num * sentence_num * str_num;
}
Chapter::~Chapter()
{
    --count;
}
//随机生成指定长度（len）字符串
string* Chapter::random_str(const int len)
{
    /*初始化*/
    string* str = new string; /*声明用来保存随机字符串的str*/
    char c;     /*声明字符c，用来保存随机生成的字符*/
    int idx;    /*用来循环的变量*/
    /*循环向字符串中添加随机生成的字符*/
    for (idx = 0; idx < len; ++idx)
    {
        /*rand()%26是取余，余数为0~25加上'a',就是字母a~z,详见asc码表*/
        c = 'a' + rand() % 26;
        (*str).push_back(c); /*push_back()是string类尾插函数。这里插入随机字符c*/
    }
    return str; /*返回生成的随机字符串*/
}

int Chapter::get_paragraph_num() { return paragraph_num; }
int Chapter::get_sentence_num(int paragraph) { return sentence_num[paragraph]; }
int Chapter::get_str_num()
{
    return sum_char;
}
void Chapter::set_paragraph_num(const int n) { paragraph_num = n; }
void Chapter::set_sentence_num(const int n) { sentence_num.push_back(n); }
string* Chapter::get_paragraph(Chapter chap, int paragragh)
{
    string * section = new string;
    for (int i = 0; i < chap.get_sentence_num(paragragh); i++)
    {
        *section = *section + *chap.chapter[paragragh][i];
    }
    return section;
}
string* Chapter::get_sentence(Chapter chap, int paragragh, int sentence)
{
   
    return chap.chapter[paragragh][sentence];
}
void Chapter::display()
{
    cout << endl;
    cout << "---------------------------------------------------" << endl;
    cout << "第" << howID() << "篇：" << endl;
    for (int i = 0; i < get_paragraph_num(); i++)
    {
        cout << "第" << i + 1 << "段：" << endl;
        for (int j = 0; j < get_sentence_num(i); j++)
        {
            cout << "第" << j + 1 << "句：" << *chapter[i][j] << endl;
        }
    }
    cout << "共" << get_str_num() << "字符" << endl;
    cout << "---------------------------------------------------" << endl;
}
int Chapter::count = 0;

#include "checkRepeat.h"

checkRepeat::checkRepeat() {}
checkRepeat::checkRepeat(Chapter& cha, vector& lib)
{
	chapter = cha;
	library = lib;
	//读取文章的段落数，每段的句子个数
	paragraph_sentence.sum_paragraph = chapter.get_paragraph_num();
	paragraph_sentence.sum_sentence.resize(paragraph_sentence.sum_paragraph);
	for (int i = 0; i < paragraph_sentence.sum_paragraph; i++)
	{
		paragraph_sentence.sum_sentence[i] = chapter.get_sentence_num(i);
	}
}
checkRepeat::~checkRepeat()
{
	for (int i = 0; i < chapter.get_paragraph_num(); i++)
	{
		delete[] pl[i];
	}
	delete[] pl;
	for (int i = 0; i < chapter.get_paragraph_num(); i++)
	{
		delete[] pls[i];
	}
	delete[] pls;
}

int** checkRepeat::paragraph_check()
{
	//创建表格进行查重数据的记录
	int** pl = new int* [chapter.get_paragraph_num()];
	for (int i = 0; i < chapter.get_paragraph_num(); i++)
	{
		pl[i] = new int[3];
		for (int j = 0; j < 3; j++)
		{
			pl[i][j] = 0;
		}
	}
	//以此获取chapter中的段落i
	for (int i = 0; i < paragraph_sentence.sum_paragraph; i++)
	{
		int plp = 0;
		//的到chapter中的第i段
		string* paragraph_inspect = chapter.get_paragraph(chapter, i);
		//依次获取library中的文章j
		for (int j = 0; j < library.size(); j++)
		{
			Chapter chapter_inspect = library[j];
			//依次检查k段
			for (int k = 0; k < library[j].get_paragraph_num(); k++)
			{
				//得library[j]到第k段
				string* temp = chapter.get_paragraph(library[j], k);
				//调用LCS,获取抄袭长度
				plp = LCS(*paragraph_inspect, *temp);
				//若超出规定要求，记录抄袭文章与段落
				if (/*(double)plp / (*paragraph_inspect).size() >= pt &&*/ plp >= pl[i][0])
				{
					//求i段抄袭文章长度
					pl[i][0] = plp;
					pl[i][1] = j;
					pl[i][2] = k;
				}
			}
		}
	}
	this->pl = pl;
	return pl;
}

int** checkRepeat::sentence_check()
{
	//创建表格进行查重数据的记录
	int** pls = new int* [chapter.get_paragraph_num()];
	for (int i = 0; i < chapter.get_paragraph_num(); i++)
	{
		pls[i] = new int[4];
		for (int j = 0; j < 4; j++)
		{
			pls[i][j] = 0;
		}
	}
	//获取chapter中的段落i
	for (int i = 0; i < paragraph_sentence.sum_paragraph; i++)
	{
		int plp = 0;
		//的到chapter中的第i段
		string* paragraph_inspect = chapter.get_paragraph(chapter, i);
		//依次获取library中的文章j
		for (int j = 0; j < library.size(); j++)
		{
			Chapter chapter_inspect = library[j];
			int paragraph_num = library[j].get_paragraph_num();
			//依次检查k段
			for (int k = 0; k < paragraph_num; k++)
			{
				int sentence_num = library[j].get_sentence_num(k);
				//依次查找z句
				for (int z = 0; z < sentence_num; z++)
				{
					//得library[j]到第k段第z句的指针
					string* temp = chapter.get_sentence(library[j], k, z);
					//调用RecursionLCS,获取抄袭长度
					plp = RecursionLCS(*paragraph_inspect, *temp);
					
					//若超出规定要求，记录抄袭文章与段落
					if (/*(double)pls[i][0] > psth &&*/ plp > pls[i][0])
					{
						//求i段抄袭文章长度
						pls[i][0] = plp;
						pls[i][1] = j;
						pls[i][2] = k;
						pls[i][3] = z;
					}
				}
			}
		}
	}
	this->pls = pls;
	return pls;
}

int checkRepeat::paragraph_repeat(int paragraph)
{
	return max(pl[paragraph][0], pls[paragraph][0]);
}

int checkRepeat::sum_repeat()
{
	int sum_repeat = 0;
	for (int i = 0; i < paragraph_sentence.sum_paragraph; i++)
	{
		sum_repeat += paragraph_repeat(i);
	}
	return sum_repeat;
}

double checkRepeat::repeat_rate()
{
	return (double)sum_repeat() / chapter.get_str_num();
}

int** checkRepeat::get_pl()
{
	return pl;
}
int** checkRepeat::get_pls()
{
	return pls;
}

void checkRepeat::set_chapter(Chapter& cha)
{
	chapter = cha;
	//读取文章的段落数，每段的句子个数
	paragraph_sentence.sum_paragraph = chapter.get_paragraph_num();
	paragraph_sentence.sum_sentence.resize(paragraph_sentence.sum_paragraph);
	for (int i = 0; i < paragraph_sentence.sum_paragraph; i++)
	{
		paragraph_sentence.sum_sentence[i] = chapter.get_sentence_num(i);
	}
}
//动态规划
int checkRepeat::LCS(const string s1, const string s2)
{
	//
	int m = s1.length() + 1;
	int n = s2.length() + 1;
	//创建二维数组表格
	int** c;
	c = new int* [m];
	for (int i = 0; i < m; i++)
	{
		c[i] = new int[n];
	}
	//初始化二维数组表格
	for (int i = 0; i < m; i++)
		c[i][0] = 0;
	for (int i = 0; i < n; i++)
		c[0][i] = 0;
	//动态规划，填写表格
	for (int i = 0; i < m - 1; i++)
	{
		for (int j = 0; j < n - 1; j++)
		{
			if (s1[i] == s2[j])
			{
				c[i + 1][j + 1] = c[i][j] + 1;
			}
			else
			{
				c[i + 1][j + 1] = max(c[i][j + 1], c[i + 1][j]);
			}
		}
	}
	//输出动态规划表格
	//for (int i = 0; i < m; i++)                
	//{
	//    for (int j = 0; j < n; j++)
	//    {
	//        cout << c[i][j] << ' ';
	//    }
	//    cout << endl;
	//}
	int result = c[m - 1][n - 1];
	for (int i = 0; i < m; i++)
	{
		delete[] c[i];
	}
	delete[]c;
	return result;
}
//蛮力法
int checkRepeat::RecursionLCS(const string s1, const string s2)
{
	int m = s1.length();
	int n = s2.length();
	int ans_lstr = 0;
	int lstr;
	for (int i = 0; i < m; i++)
	{
		for (int j = 0; j < n; j++)
		{
			lstr = 0;
			//相当于，从相等的位置,开始比较
			if (s1[i] != s2[j]) { continue; }
			//取相等之后的字符串进行比较
			string str1 = s1.substr(i), str2 = s2.substr(j);
			int size = min(str1.size(), str2.size());
			for (int k = 0; k < size; k++)
			{
				++lstr;
			}
			//比较此次获得的连续字符串与之前相比哪个更长
			ans_lstr = max(ans_lstr, lstr);
		}		
	}
	return ans_lstr;
}

#include "control.h"

Chapter text;
vector lib;
checkRepeat opter;

void Init()
{
	for (int i = 0; i < 10; i++)
	{
		Chapter temp;
		lib.push_back(temp);
	}
	text.display();
	opter.set_chapter(text);
	opter.set_library(lib);
}

void start()
{
	opter.paragraph_check();
	opter.sentence_check();
	double rate = opter.repeat_rate();
	cout << "文章查重率为：" << opter.repeat_rate() * 100 << "%" << endl;
	if (rate >= opter.get_pt())
	{
		//输出该文章的抄袭段落
		int** table = opter.get_pl();
		int paragraph_num = text.get_paragraph_num();
		for (int i = 0; i < paragraph_num; i++)
		{
			double paragraph_rate = (double)table[i][0] / (*(text.get_paragraph(text, i))).size();
			if (paragraph_rate > opter.get_pt())
			{
				int sentence_num = text.get_sentence_num(i);
				cout << "第" << i << "段：";
				cout << "\t&段落重复率：" << paragraph_rate * 100 << "%";
				cout << "\t@出自chapter:" << table[i][1] << "第" << table[i][2] << "段" << endl;
				for (int j = 0; j < sentence_num; j++)
				{
					cout << "第" << j << "句：";
					cout << *(text.get_sentence(text, i, j)) << endl;
				}
				cout << "抄袭段落：" << endl;
				cout << *text.get_paragraph(lib[table[i][1]], table[i][2]) << endl;
			}
		}
	}
}

void display_repeat()
{
	//输出该文章的抄袭的文章的段落
	int** table = opter.get_pl();
	int** table2 = opter.get_pls();
	int paragraph_num = text.get_paragraph_num();
	for (int i = 0; i < paragraph_num; i++)
	{
		double paragraph_rate = (double)table[i][0] / (*(text.get_paragraph(text, i))).size();
		if (paragraph_rate > opter.get_pt())
		{
			cout << "第" << i << "段抄袭chapter" << table[i][1] << endl;
			//输出第i篇文章
			//获取第table[i][1]篇文章的段落数
			int repeat_paragraph_num = lib[table[i][1]].get_paragraph_num();
			//循环输出段落
			for (int j = 0; j < repeat_paragraph_num; j++)
			{
				cout << "第" << j << "段：" << endl;
				//获取j段落的句子数
				int repeat_sentence_num = lib[table[i][1]].get_sentence_num(j);
				//循环句子输出
				for (int k = 0; k < repeat_sentence_num; k++)
				{
					cout << "第" << k << "句：";
					if (table2[i][3] == k && table2[i][2] == j && table2[i][3] > 0)
					{
						//黄色输出
						cout << "\033[33;1m" << *(text.get_sentence(lib[table[i][1]], j, k)) << "\033[0m" << endl;
					}
					else if (table[i][2] == j)
					{
						//红色输出
						cout << "\033[31;1m" << *(text.get_sentence(lib[table[i][1]], j, k)) << "\033[0m" << endl;
					}
					else
					{
						//正常输出
						cout << *(text.get_sentence(lib[table[i][1]], j, k)) << endl;
					}
				}
			}
		}
	}
}

#pragma once
#include "chapter.h"
#include "checkRepeat.h"
#include 
#include 
using namespace std;

void Init();
void start();
void display_repeat();

#include 
#include "chapter.h"
#include "control.h"
#include "checkRepeat.h"

using namespace std;

int main()
{
	bool quit = true;
	Chapter text;
	/* cout << *temp.get_paragraph(temp, 2) << endl;*/
	do
	{
		int key;
		cout << "###########################" << endl;
		cout << "#------文章查重系统-------#" << endl;
		cout << "#\t1、生成文章：\t  #" << endl;
		cout << "#\t2、抄袭率：\t  #" << endl;
		cout << "#\t3、查看抄袭段落： #" << endl;
		cout << "#\t4、退出\t\t  #" << endl;
		cout << "###########################" << endl;
		cout << "请选择（1-4）:";

		cin >> key;
		switch (key)
		{
		case 1:
		{
			Init();
			break;
		}
		case 2:
		{
			start();
			break;
		}
		case 3:
		{
			display_repeat();
			break;
		}
		case 4:
			quit = false;
		default:
			break;
		}

	} while (quit);
}

三、果园篱笆问题

3.1 问题描述

某大学ACM集训队，不久前向学校申请了一块空地，成为自己的果园。全体队员兴高采烈的策划方案，种植了大批果树，有梨树、桃树、香蕉……。后来，发现有些坏蛋，他们暗地里偷摘果园的果子，被ACM 集训队队员发现了。因此，大家商量解决办法，有人提出：修筑一圈篱笆，把果园围起来，但是由于我们的经费有限，必须尽量节省资金，所以，我们要找出一种最合理的方案。由于每道篱笆，无论长度多长，都是同等价钱。所以，大家希望设计出来的修筑一圈篱笆的方案所花费的资金最少。有人己经做了准各工序，统计了果园里果树的位置，每棵果树分别用二维坐标来表示，进行定位。现在，他们要求根据所有的果树的位置，找出一个n边形的最小篱笆，使得所有果树都包围在篱笆内部，或者在篱笆边沿上。
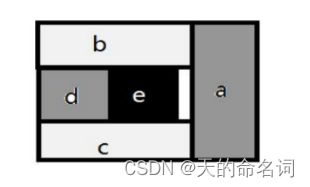
本題的实质：凸包问题。请使用蛮力法和分治法求解该问题，
1、至少用两种方法设计该问题的第法，
2、用程序实现两种算法，并给出两种算法运行结果的比较，要有图形化的界面
3、文档要求给出重要算法的算法设计的基本方法（分治，动态规划、贪心、
回溯等)，选用这些设计方法的原因，给出该算法的伪代码，分析该算法的时间
复杂度，给出算法实际运行的结果

3.2 解决问题所用的方法及基本思路

分治法：

取横坐标最小的点p0和横坐标最大pn的点，然把这两个点连成一条直线，直线上面的半个凸包叫上凸包，直线下面的半个凸包叫下凸包，分别在上凸包和下凸包找出距离直线最大的点pmax，链接p1pmax和pnpmax，又可以把上下两个凸包分解成更小的上凸包和下凸包。直到上凸包函数内点全为下凸包，下凸包函数内点全为上凸包，则该点为凸包点。

蛮力法：

原始蛮力法算法思想是对所有坐标点进行遍历，每两个组成一条直线，以直线为基准线，对剩余所有坐标点进行距离计算，若所有点都在直线某一侧，则此坐标点为凸包点；此种方法时间复杂度达到了o（n3）级，复杂度过高。对此，进行了一些改进算法：

把所有点放在二维坐标系中，则纵坐标最小的点一定是凸包上的点，如图中的P0。

图3-1

计算各个点相对于 P0 的幅角 α ，按从小到大的顺序对各个点排序。当 α 相同时，距离 P0 比较近的排在前面。例如上图得到的结果为 P1，P2，P3，P4，P5，P6，P7，P8。我们由几何知识可以知道，结果中第一个点 P1 和最后一个点 P8 一定是凸包上的点。（以上是准备步骤，以下开始求凸包）

我们已经知道了凸包上的第一个点 P0 和第二个点 P1(已经满足第1，2个条件)。

至于第3个条件，我们可以借助一下数学思想。（叉积）：当两个向量的叉积大于等于零时，则满足条件。反之则不满足条件。

通过遍历依次判断每个坐标，当向量p2p3在向量p1p2右边时（如上图所示），我们需要回溯将之前存储在p2[]中的p2点删除，并将p3添加到p2[]中。

就这样一直遍历下去。直到回到p0；

拓展功能：

对凸包点按一定顺序进行排序并求出每两凸包点间距离，即为围篱笆所需周长。

3.3 采用的数据结构描述

分治法：
数组
蛮力法：
数组、栈

3.4 算法描述

 分治法：
Dhull(x,y)
   //求解下凸包，分界线为下标x的点指向y的点
   //输入：下标x，下标y
   //输出：凸包点
   Dis<- -1, j<- -1
   if p.x <= p.y
L<- x
R<- y
   else 
L<-y
R<-x
   for i <- L+1 to R-1 do
If multi(p[x],p[y],p[i] <=0) do
If(dist(p[x],p[y],p[i]) > dis do
    dis <- dist(p[x],p[y],p[i])
    j=i
   if j==-1 do
S[m++] <- p[x]
   if multi(p[x],p[j],p[y])<0 do
       uh <- x
       dh <- y
else
       uh <- y
       dh <-x
Dhull(dh,j)
Uhull(uh,j)
Return S




Uhull(x,y)
   //求解上凸包，分界线为下标x的点指向y的点
   //输入：下标x，下标y
   //输出：凸包点
   Dis<- -1, j<- -1
   if p.x <= p.y
L<- x
R<- y
   else 
L<-y
R<-x
   for i <- L+1 to R-1 do
If multi(p[x],p[y],p[i] >=0) do
If(dist(p[x],p[y],p[i]) > dis do
    dis <- dist(p[x],p[y],p[i])
    j=i
   if j==-1 do
S[m++] <- p[x]
   if multi(p[x],p[j],p[y])<0 do
       uh <- x
       dh <- y
else
       uh <- y
       dh <-x
Dhull(dh,j)
Uhull(uh,j)
return S

蛮力法：
convex_hull(n,p[0,n-1])
//利用栈的思想求解凸包问题
//输入：待处理顶点个数及顶点坐标
//输出：凸包点
sort(p,p+n,cmp)//极角排序
s[0]<-p[0]
S[1]<-p[1]
Top <- 1
for i <-2 to n-1 do 
while (multi(s[top-1], s[top],p[i])<0 do
Top--
    S[++top]=p[i]
return S

3.5 算法的时间空间复杂度分析

给出基本的运算是什么？

分治法：比较大小

蛮力法：比较大小出栈、入栈

分治法：M(n)=2M(n-1)+1

蛮力法：外侧循环遍历N，内侧使用堆栈搜索顶点是LogN，所以是NLogN

时间复杂度：

分治法：o(nlogn)

蛮力法：o(nlogn)

3.6 代码

分治法：

#include 
#include 
#include 
#include 
#include 
#include 
#define PI acos(-1.0)
#define eps 1e-9

using namespace std;

struct node
{
	double x, y;
};

node p[110], s[110];
int m;

double multi(node p1, node p2, node p3);

bool cmp(node a, node b);

double dist(node p1, node p2, node p3);

double distd(node a, node b);

void convex_hull(int n);

void uhull(int x, int y);

void dhull(int x, int y);

int main()
{
	int n, i;

	double d;

	m = 0;

	cout << "请输入待处理篱笆顶点个数" << endl;

	cin >> n;

	for (i = 0; i < n; i++) {

		cout << "请输入第" << i + 1 << "个坐标点" << endl;

		cin >> p[i].x >> p[i].y;
	}

 	convex_hull(n);

	double sum = 0;

	for (i = 0; i < m; i++)
	{
		
		//取余目的令周长形成闭环，否则出现溢出导致结果错误
		sum += distd(s[i], s[(i + 1) % m]);
	}

	cout << "篱笆应放置点为" << endl;

	for (i = 0; i < m; i++)
	{

		cout << s[i].x << ',' << s[i].y << endl;

	}

	cout << "篱笆长度为" << endl;

	cout << sum << endl;

	system("pause");

	return 0;
}

//求p3点到p1p2直线的距离
double dist(node p1, node p2, node p3)
{

	return abs((p2.y - p1.y) * p3.x + (p1.x - p2.x) * p3.y + (p1.y - p2.y) * p1.x + (p2.x - p1.x) * p1.y) / sqrt(pow(p2.y - p1.y, 2) + pow(p1.x - p2.x, 2));

}

/*判断第三个点在直线的左方还是右
如果该式的值大于0，p3在p1p2形成直线的左侧，小于0在右侧，等于0在直线上。*/
double multi(node p1, node p2, node p3)
{

	return p1.x * p2.y + p3.x * p1.y + p2.x * p3.y - p3.x * p2.y - p2.x * p1.y - p1.x * p3.y;

}

//按x升序重载排序规则，如果x相同按照y升序
bool cmp(node a, node b)
{

	if (abs(a.x - b.x) <= eps)

		return a.y < b.y;

	return a.x < b.x;
}

//求两点间距离
double distd(node a, node b)
{

	return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2));

}

//按照横坐标升序排序之后，下标为0的点和下标为n-1的点连线将凸包分成上下两个凸包
void convex_hull(int n)
{
	//对输入坐标点进行排序
	sort(p, p + n, cmp);
	//分治进入下凸包
	dhull(0, n - 1);
	//分治进入上凸包
	uhull(0, n - 1);

}

//求解下凸包，分界线为下标为x的点指向下标为y的点
void dhull(int x, int y)
{

	int i, j, l, r;
	//初始化直线距离
	double dis = -1;

	j = -1;

	if (x <= y)
	{

		l = x;

		r = y;

	}
	else
	{

		l = y;

		r = x;

	}
	//无论是上凸包还是下凸包所要找的最远点的横坐标的最小值肯定不会小于p[l].x的最小值，
	//最大值肯定不会大于p[r].x,而我们的点是按照横坐标升序的所以只需遍历(l,r)
	for (i = l + 1; i < r; i++)
	{

		if (multi(p[x], p[y], p[i]) <= 0)//下凸包问题所找点位于线段右侧
		{

			if (dist(p[x], p[y], p[i]) > dis)//判断距离直线的距离，若大于则更新距离形成新的凸包点
			{

				dis = dist(p[x], p[y], p[i]);

				j = i;

			}
		}
	}

	//未找到最远点那么这两个点是在凸包上直接相连的两个点
	if (j == -1)
	{

		s[m++] = p[x];

		return;
	}
	int uh, dh;

	/*
	p[x]p[y]是当前半个凸包的分界线，如果p[y]在p[x]p[j]的
	右方，p[j]为pmax，那么下一个pmax肯定在p[x]p[j]的左方，p[y]p[j]的右方。
	否则pmax在p[x]p[j]的右方，p[y]p[j]的左方。
	这样就能直接判断哪个是上凸包，哪个是下凸包。
	*/
	if (multi(p[x], p[j], p[y]) < 0)
	{

		uh = x;

		dh = y;

	}
	//否则在右侧
	else
	{

		uh = y;

		dh = x;

	}

	dhull(dh, j);

	uhull(uh, j);

}

//求解上凸包问题

void uhull(int x, int y)
{

	int i, j, l, r;

	double dis = -1;

	j = -1;

	if (x <= y)
	{

		l = x;

		r = y;

	}
	else
	{

		l = y;

		r = x;

	}
	for (i = l + 1; i < r; i++)
	{

		if (multi(p[x], p[y], p[i]) >= 0)//上凸包问题所需点位于线段左侧
		{

			if (dist(p[x], p[y], p[i]) > dis)
			{

				dis = dist(p[x], p[y], p[i]);

				j = i;

			}
		}
	}
	if (j == -1)
	{

		s[m++] = p[y];

		return;

	}
	int uh, dh;

	if (multi(p[x], p[j], p[y]) <= 0)
	{

		uh = x;

		dh = y;

	}

	else
	{

		uh = y;

		dh = x;

	}

	dhull(dh, j);

	uhull(uh, j);

}

蛮力法：

#include 
#include 
#include 
#include 
#include 
#include 
#define inf 0x3f3f3f3f
#define pi acos(-1.0)
//定义eps为无穷小以减少数据类型带来的误差
#define eps 1e-9
using namespace std;

/*思路：Graham扫描的思想是先找到凸包上的一个点，然后从那个点开始按逆时针方向逐个找凸包上的点，
实际上就是进行极角排序，然后对其查询使用。 */

struct node
{
    
    double x, y;

};

node p[1100];

node s[1100];

//动态更新最小结点
node minp;

int top;
//判断x是否小于等于0
bool equal(double x)
{

    return abs(x - 0) <= eps;

}

/*判断第三个点在直线的左方还是右
如果该式的值大于0，p3在p1和p2形成直线的左侧，小于0在右侧，等于0在直线上。*/
double multi(node p1, node p2, node p3)
{

    return p1.x * p2.y + p3.x * p1.y + p2.x * p3.y - p3.x * p2.y - p2.x * p1.y - p1.x * p3.y;

}

//求两点间距离
double distence(node a, node b)
{

    return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));

}

bool cmp(node a, node b)
{
    //若b点位于顶点与a点直线右侧或在直线上
    if (equal(multi(minp, a, b)))

        return distence(minp, a) - distence(minp, b) < 0;

    return multi(minp, a, b) > 0;

}

//找凸包点
void convex_hull(int n)
{
    //进行极角排序,使得坐标点以逆时针排序
    sort(p, p + n, cmp);

    s[0] = p[0];

    s[1] = p[1];

    top = 1;

    for (int i = 2; i < n; i++)
    {
        //若该点位于直线左侧，则抛弃该点，出栈
        while (multi(s[top - 1], s[top], p[i]) < 0)

            top--;

        s[++top] = p[i];
    }
}

int main()
{
    //n为待处理坐标点个数
    int n, i;
    //sum为最终周长
    double sum;

    cout << "请输入待处理篱笆顶点个数" << endl;

    while (cin >> n)
    {
        //栈顶指针
        top = 0;

        sum = 0;
        //初始化最小顶点为无穷大
        minp.x = inf;

        minp.y = inf;

        for (i = 0; i < n; i++)
        {

            cout << "请输入第" << i + 1 << "个坐标点" << endl;

            //输入所有待处理坐标点
            cin >> p[i].x >> p[i].y;
            //寻找扫描顶点，其特征为x、y值为所有坐标点中最小的，以y值为优先判断条件
            if (p[i].y < minp.y || (p[i].y == minp.y && p[i].x < minp.x))
            {

                minp.x = p[i].x;

                minp.y = p[i].y;

            }

        }

        convex_hull(n);

        top++;

        for (i = 1; i <= top; i++)
        {

            //取余目的令周长形成闭环，否则出现溢出导致结果错误
            sum += distence(s[i %top], s[(i + 1)%top]);

        }

        cout <<"篱笆应放置点为"<

 
  四、基因序列比较 
  4.1 问题描述 
   
    人类基因由4种核苷酸，分别用字母ACTG表示。要求编写一个程序，按以下规划比较两个基因序列并确定它们的相似程度。即两 
    给出两个基因序列AGTGATG和GTTAG，它们有多相似呢？测量两个基因的相似度一种方法称为对齐。使用对齐方法可以在基因的适当位置加入空格，让两个基因的长度相等，然后根据基因的分值矩阵计算分数。 
   
    
     
      
  
      A
  
      C
  
      G
  
      T
  
      -
  
     
     
      A
  
      5
  
      -1
  
      -2
  
      -1
  
      -3
  
     
     
      C
  
      -1
  
      5
  
      -3
  
      -2
  
      -4
  
     
     
      G
  
      -2
  
      -3
  
      5
  
      -2
  
      -2
  
     
     
      T
  
      -1
  
      -2
  
      -2
  
      5
  
      -1
  
     
     
      -
  
      -3
  
      -4
  
      -2
  
      -1
  
      *
  
     
    
   
  比较AGTGATG与GTTAG 
  第一种对齐方案为： 
  首先可以给AGTATG插入一个空格得：AGTAT-G 
           GTTAG插入3个空格即得：-GT--TAG 
  上面的匹配分值为:-3+5+5+(-2)+(-3)+5+(-3)+5=9. 
  第二种对齐方案为： 
  AGTGATG 
  -GTTA-G 
  得到的分值为：(-3)+5+5+(-2)+5+(-1)+5=14. 
    当然还有其它对齐方式，但以上对齐方式是最优的，所以两个基因的相似度就为14。 
  4.2 解决问题所用的方法及基本思路 
    问题是判断基因序列的相似度，可以用动态规划和减治的方法进行求解。减治法每一次先求解出更小一规模的子问题，再将小规模问题的解进行合并。动态规划法是采用自下而上的方式求值，并把中间最优结果存储起来。 
    根据题目的对齐方式，设两条基因序列分别为长度为m的X序列和长度为n的Y序列，可以理解为要找一条由坐标（0,0）到坐标（m-1，n-1）的路径，规则是只能向下、向右或者向右下走，使得这条路径的值最高,方式如下图所示： 
   
    
   
  图4-1题目的抽象结果 
      两序列对比的过程用二维数组dp[i][j]显示，其中i表示的是第一个序列X的第i个元素，j表示的是第二个序列Y的第j个元素，矩阵中的每一元素可表示第一个序列X已比对字母且第二个序列Y已比对字母相同比对结果的最优者，右下格就是整个比对的最优结果。 
    可以看到，原来的插值、匹配问题已经被转换成一个二维寻址问题，每一步的选择是向下、向右或者向右下走，使得这条路径的值最高。 
    具体计算时每一格只用最优比对的得分表示，给出的长度为m的X序列和长度为n的Y序列，建立一个（m+2）*（n+2）的矩阵，函数dp[i][j]递归求序列X[1...i]和Y[1....j]的最佳比配的得分，建立以下状态转移方程： 
  dp[i][j]=max{dp[i-1][j-1]+score(X[i],Y[j]),dp[i-1][j]+score(X[i],’-’),dp[i][j-1]+score(‘-’,Y[j])} 
  具体过程应该如下： 
   
   建立得分表：以第一个序列X序列为竖，以第二个序列Y序列为横，建立（m+2）*（n+2）矩阵，Y序列从第一行第三列开始填入，X序列从第一列第三行开始填充，如下图所示： 
   
   
   图4-2 table的初始化 
   
      2、选择得分体系，采用题目中给出的分值表 
      3、填充得分表，通过矩阵一行一行，从左向右地移动，计算每个位置的分数，每一个单元格的结果，是从左、上或左上结果位移而来，最后从这三者中取出最大值与该单元格的得分值相加，用箭头指向得分的来源。根据上面的转移方程得出分值，如下图所示。 
   
    
   
  图4-3 table的填充 
      4、回溯得出最优解：表右下角的位置的值即为解，通过回溯这个值的来源，一直回溯到顶部，得到对齐方式。 
    回溯法的解决思路和动态规划非常相似，唯一的区别就在于动态规划是自底向上，而回溯法是自顶向下的。若想达到右下角最大值的效果，那么就需要回溯其左，上，左上的结果，依此回溯到初始条件，在继续向下进行，即可得到结果。其状态空间树如下图： 
   
     
   
  图4-4 基因配对的状态树 
  4.3 算法描述 
  动态规划算法 ACTG(m,n)
//输出：m表示X序列的长度，n表示Y序列的长度
//输出：得分最大的值
初始化数组f[m+1][n+1]
For i←1 to m：
 For j←1 to n：
  if  n=1
dp[i][0]=dp[i-1][0]+score(X[j],’-’)
Return dp[i][0]
      if  m=1
dp[0][j]=dp[0][j-1]+score(‘-’,Y[j])
Return dp[0][j]
      else:
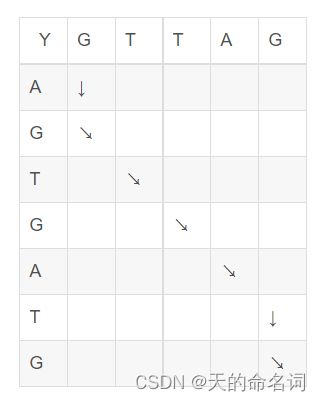
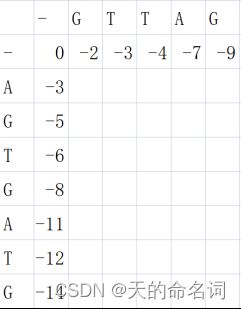
dp[i][j]=max{dp[i-1][j-1]+score(X[i],Y[j]),dp[i-1][j]+score(X[i],’-’),dp[i][j-1]+score(‘-’,Y[j])}
   return dp[m-1][n-1]

减治算法ATCG1(X,Y,m,n,res[0..m][o...n])
// 输入：基因序列X,Y,基因序列的长度m,n，以及一个二维数组
// 输出：二维数组最下方的元素
if m > 0 and n > no
Then
res[m][n]=max(
ATCG1(X,Y,m-1,n-1,res)+
get(x.substring(m-1,m),y.substring(n-1,n),
ACTG1(x,y,m-1,n,res)+get(x.substring(m-1,m),"-"),
ACTG1(x,y,m,n-1,res)+get("-",y.substring(n-1,n)
) 
  4.4 算法时间空间复杂度分析 
  基本运算：比较操作 
  基本运算的重复执行次数的表达式：C(n) = m*n 
  时间复杂度渐进表示：O(mn) 
  空间复杂度渐进表示：O(mn) 
    当在序列中插入一个空字符串时，需要新建两个数组来存放新的序列，这步操作花费了m+n的时间。在初始化时有m+n次赋值操作，加上运算时m×n次赋值操作，一共(m×n)+m+n次赋值，所以最后的时间复杂度为O(mn)。 
    因为运算时，创建了一个记录结果的表，所以空间复杂度为（m+2)×(n+2)，所以最后的空间复杂度为O(mn)。 
  4.5 算法实例 
   
   图4-5 基因配对的输入和输出结果 
  4.6 代码 
  import java.io.File;
import java.io.FileWriter;
import java.io.IOException;


//序列比较
class ACGTCompare{
	String s1;
	String s2;
	public int[][] arrayTable;
	public String Ns1;//变更后的x序列
	public String Ns2;//变更后的y序列

	public ACGTCompare(String s1,String s2) throws IOException {
		this.s1=s1;
		this.s2=s2;
		arrayTable=new int[s1.length()+1][s2.length()+1];
		Fill_Table();
		getS();   //变更后的s1和s2
	}
	//检查序列字符串格式是否正确
	public static boolean IsRight_s(String string) {
		for(int i=0;imax?b:max;
		max=c>max?c:max;
		return max;
	}
}
 
  import java.io.IOException;
import java.util.Scanner;


public class ACTG{
	public static void main(String[] args) throws IOException {
//		用作测试题目所给的序列，验证是否测试正确
		Scanner scanner = new Scanner(System.in);
		System.out.println("请输入第一个序列：");
		String X = scanner.next();
		System.out.println("请输入第二个序列：");
		String Y = scanner.next();
		ACGTCompare c=new ACGTCompare(X,Y);
		System.out.println(c.getResult());
		System.out.println(c.Ns1);
		System.out.println(c.Ns2);
	}
}
 
  package experiment5;

import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;

import static sun.swing.MenuItemLayoutHelper.max;
public class ACTG1 {
	public static void main(String[] args){
		Scanner scanner = new Scanner(System.in);
		System.out.println("请输入第一个序列：");
		String X = scanner.next();
		System.out.println("请输入第二个序列：");
		String Y = scanner.next();
		int m = X.length();
		int n = Y.length();
		int[][] res = new int[m+1][n+1];
		res[0][0] = 0;
		for(int i = 1;i <= m;i++){
			res[i][0] = res[i-1][0] + get(X.substring(i-1,i),"-");
		}
		for(int j = 1;j <= n;j++){
			res[0][j] = res[0][j-1] + get("-",Y.substring(j-1,j));
		}
		System.out.println("这两个基因序列的相似度为：" + Similarity(X,Y,m,n,res));
	}
	public static int Similarity(String x,String y,int m,int n,int[][] res){
		if(m > 0 && n > 0){
			res[m][n] = max(Similarity(x,y,m-1,n-1,res)+get(x.substring(m-1,m),y.substring(n-1,n)),
					Similarity(x,y,m-1,n,res)+get(x.substring(m-1,m),"-"),
					Similarity(x,y,m,n-1,res)+get("-",y.substring(n-1,n)));
		}
		return res[m][n];
	}
	public static int get(String a,String b){
		Map map = new HashMap<>();
		map.put("A",0);
		map.put("C",1);
		map.put("G",2);
		map.put("T",3);
		map.put("-",4);
		int[][] score = {{5,-1,-2,-1,-3},
				{-1,5,-3,-2,-4},{-2,-3,5,-2,-2},
				{-1,-2,-2,5,-1},{-3,-4,-2,-1,0}};
		return score[map.get(a)][map.get(b)];
	}
} 
  五、地图着色问题 
  5.1 问题描述 
  1．设计内容： 
  已知中国地图，对各省进行着色，要求相邻省所使用的颜色不同，并保证使用的颜色总数最少。 
  2．设计要求： 
  （1）设计该问题的核心算法； 
  （2）设计可视化的界面，界面中能显示和区分中国地图中各省、市、自治区； 
  （3）程序能正确对地图着色。 
  5.2 解决问题所用的方法及基本思路 
    本题抽象出来其实就是着色问题：已知一个图，要求给图上每个点上色，并保证该点的颜色与它的邻接点的颜色都不相同。 
    利用回溯法，回溯法的基本思想是：在解空间中，按深度优先策略，从根结点出发搜索，搜索至任一节点时，先判断该节点是否包含问题的解。如果不包含，则跳过以该节点为根的子节点，逐层向其父节点回溯。否则，进入该子树，继续按照深度优先策略搜索。 
    问题有两个要求，一个是相邻的省使用的颜色不同，另一个是使用的颜色最少。 
    为保证第一个要求，在给每一个省份上色前，要排除相邻的省份已使用的过的颜色，使用剩余颜色中的第一种颜色上色，完成后将该颜色排除，若回溯，会初始化部分省份的颜色。在上色前，将邻接省份已用的颜色赋值为0，使用时使用第一个不为0的颜色值。 
    为了保证第二个要求，首先使用两种颜色，若在着色时失败则增加到三种颜色进行着色，若三种颜色着色失败，则增加到第四种颜色，直至使用最少的颜色着色成功。着色成功后用下一个省份的颜色作为第一个省份开始着色，重复上述步骤，直至使用所有省份作为第一个着色省份开始着色，并用最少的颜色成功着色，再通过比较各个省份作为第一个着色省份开始着色，着色成功是所需最少的颜色数，得出着色需要的最少的颜色数。 
    假设地图邻接关系如图5-1所示，那么它的状态解空间树如图5-2所示： 
   
   图5-1 地图邻接关系 
   
    图5-2 状态解空间树 
  5.3 算法描述 
  算法 Map_Color（s[0....n]）
//输入：s[0...n]表示省
//输出：0或1,1表示着色成功，符合要求；0表着色失败，不符合要求
n=33；//中国34个省
s[0]=1;//选择第一个区域先着色，颜色为1
area=1；//从第二个区域开始着色
color=0；//从颜色1开始着色
if area >= 33  //如果完成34个省份的着色，
return  1;
for i←0 to 3 //从第一个颜色开始着色
S[area] ← i;
m←0;
for j←0 to area  //判断当前着色是否合理
if metrix[area][j] == 1 and s[j] == s[area]
m←1;
if m==1
count++;
k = Map_Color(s[0...n]);  //递归调用着色函数进行着色
if k==-1    //如果不合理，则进行回溯操作
area--;
s[area] = -1;
if area>33    //如果所有省份被着色，返回1
return 1;
if i>=4
  return -1;
return 1; 
  5.4 算法的时间空间复杂度分析 
  基本运算：比较操作 
  基本运算的重复执行次数的表达式：C(n) = 
  时间复杂度渐进表示：O() 
  空间复杂度渐进表示： 
  空间复杂度上，有用于记录地图中不同区域的邻接关系的邻接链表，有用于记录每一个区域颜色的栈，设地图中区域的个数为n,则有邻接表的大小为n*n,存储每一个区域颜色的栈的大小是n,总的空间用量是n*n+n,所以空间复杂度为。 
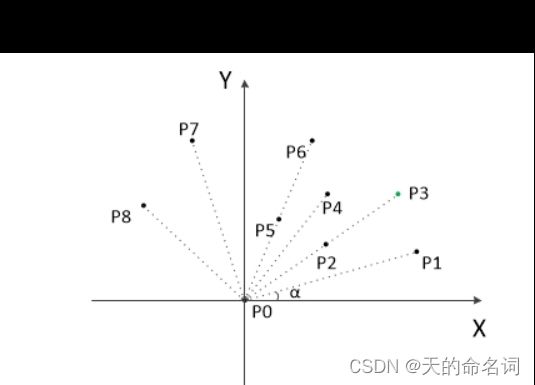
  在时间复杂度上，平均情况为 O(),主要与n的规模有关。 
  5.5 算法实例 
  输入：各省份的邻接矩阵以及颜色的数量 
  输出： 
   
    
   
  图5-1 着色结果 
  5.6 代码 
  package experiment6.MAP;

import java.awt.Checkbox;
import java.awt.Graphics;
import java.awt.Polygon;
import java.awt.Robot;
/**
 * 说明：
 * robot类用于为测试自动化、自运行演示程序和其他需要控制鼠标和键盘的应用程序生成本机系统输入事件。
 * 主要屏幕截图，延时，取屏幕颜色，模拟键盘，模拟鼠标
 */
public class Map1 {
	private MapColor mc;
	@SuppressWarnings("unused")
	private Polygon[] p;//定义多边形
	private Checkbox cbx;
	private int count = 0;//初始化着色个数为0
	int[][] metrix;
	public Map1(MapColor mc,Polygon[] p,Checkbox cbx,int[][] metrix){
		this.mc = mc;
		this.p = p;
		this.cbx = cbx;
		this.metrix =metrix;
	}
	//判断函数
	public boolean isOK(int province[])
	{
		for(int j=0;j=33;
		if(isAllProvincesColorful) {//如果着色的个数小于33，因为设置了34个省级行政区
			return 1;
		}
		//从第一个颜色开始着色，给与了四种颜色
		for(i=0;i<4;i++)
		{
			province[count]=i;
			Graphics g = mc.getGraphics();
			mc.fillColor(g, count, i);
			//如果演示被选择，则使用Robot的延时功能，进行演示
			boolean isIllustrate = cbx.getState();
			if(isIllustrate) {
				try{
					Robot r = new Robot();
					r.delay(150);
				}
				catch(Exception e){}
			}
			/**
			 * isok（）判断当前着色是否合理（即不是相邻且同色的），
			 * 如果不合理，执行最开始的步骤，重新赋予颜色，
			 * 如果合理执行下一个颜色的着色
			 * */
			if(isOK(province)){
				count++;
				int j = color(province); //递归调用着色函数进行着色
				/**
				 * 当现在这个省的颜色与相邻的省颜色相同
				 * 回到上一个颜色
				 * 重置上一个省的颜色
				 * */
				if(j==-1){
					count--;
					province[count]=-1;
				}
				if(count>33) return 1;//如果所有省份都被着色，返回1
			}
		}

		if(i>=4) return -1;//如果着色颜色超过了4，就错误，返回-1
		return 1;
	}

	//定义省份一维数组，对省份进行着色
	public void backtrack(){
		int province[]=new int[34];
		color(province);
	}
	//重置按钮
	public void resetMap(){
		Graphics g = mc.getGraphics();
		for(int k=0;k<34;k++){
			mc.fillColor(g, k, 4);
		}
		mc.paint(g);
	}
}
 
  package experiment6.MAP;

import java.awt.*;
import java.awt.event.*;

public class Map2 {

	//使用多边形来表示省级行政区
	public static int[][] p_x = {{21,178,234,164,48,},//5
			{48,164,164,232,239,165,83},//7
			{230,239,272,288,306,290,294,307,256,220},//10
			{164,196,285,264,230,232,164},//7
			{230,264,279,315,337,325,310,314,288,272,239},//11
			{290,306,314,312,334,347,347,294},//8
			{196,234,240,306,314,330,341,320,315,279,264,285},//12
			{240,311,436,402,433,472,468,306},//8
			{306,327,330,314},//4
			{433,471,522,558,538,469,472},//7
			{469,538,496,468},//4
			{430,468,496,460,461,442,},//6
			{330,327,366,350,337,315,320,341},//8
			{366,393,386,357},
			{404,411,421,413},
			{413,421,430,424},
			{393,430,442,430,411,404,424,426,410,386},//10
			{357,386,410,407,354},
			{410,426,469,443,409},
			{310,325,337,350,355,338,347,347,334,312},//10重庆
			{338,355,350,354,407,413,394,347},//8//21
			{407,409,418,446,438,413},//6
			{418,443,474,453,446},
			{453,463,475,463},
			{438,446,453,477,462},
			{347,394,394,373,361,347},//6
			{294,361,373,352,323},
			{394,413,438,443,431,420,394},
			{420,431,443,462,451,433},
			{352,373,394,420,433,404,401,396,398,395,392,387,390,359,357,352},
			{396,401,404,398},
			{387,392,395,390},
			{339,362,364,351,338},
			{466,474,484,476}};
	public static int[][] p_y= {{120,49,134,199,194},
			{194,199,232,260,297,314,268},
			{300,297,331,311,317,330,353,369,394,353},
			{199,171,207,256,240,260,232},
			{240,256,241,260,265,287,295,318,311,331,297},
			{330,317,318,308,304,314,341,353},
			{170,134,136,206,228,199,217,233,260,241,256,207},
			{136,151,89,77,9,28,125,206},
			{206,195,199,228},
			{9,6,58,47,113,92,28},
			{92,113,149,125},
			{145,125,149,178,153,168},
			{199,195,177,266,265,260,233,217},
			{177,163,217,235},
			{172,162,172,180},
			{180,172,180,189},
			{163,145,168,180,162,172,189,193,220,217},
			{235,217,220,270,249},
			{220,193,200,228,231},
			{295,287,265,266,279,288,298,314,304,308},//重庆
			{288,279,266,249,270,290,298,298},//9
			{270,231,230,272,297,290},
			{230,228,267,272,272},
			{272,270,274,278},
			{297,272,272,286,321},
			{298,298,344,356,338,341},//6
			{353,338,356,392,390},
			{298,290,297,303,313,351,344},
			{351,313,303,321,347,364},
			{392,356,344,351,364,377,372,375,379,380,376,379,383,396,404,404},
			{375,372,377,379},
			{379,376,380,383},
			{417,411,414,431,429},
			{371,342,342,381}};
	//通过metrix数组，定义了34个省，如果相邻则为1,不相邻为0
	public static int metrix[][]={{0,1,0,1,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},//1新疆
			{1,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},//2西藏
			{0,1,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0},//3云南
			{1,1,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},//4青海
			{0,1,1,1,0,1,1,0,0,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0},//5四川
			{0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,1,1,0,0,0,0,0,0,0},//6贵州
			{1,0,0,1,1,0,0,1,1,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},//7甘肃
			{0,0,0,0,0,0,1,0,1,1,1,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},//8内蒙古
			{0,0,0,0,0,0,1,1,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},//9宁夏
			{0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},//10黑龙江
			{0,0,0,0,0,0,0,1,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},//11吉林
			{0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},//12辽宁
			{0,0,0,0,1,0,1,1,1,0,0,0,0,1,0,0,0,1,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0},//13陕西
			{0,0,0,0,0,0,0,1,0,0,0,0,1,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},//14山西
			{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},//15北京
			{0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},//16天津
			{0,0,0,0,0,0,0,1,0,0,0,1,0,1,1,1,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},//17河北
			{0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,1,0,1,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0},//18河南
			{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0},//19山东
			{0,0,0,0,1,1,0,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,1,0,0,0,0,0,0,0,0},//20重庆
			{0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,1,0,1,0,1,0,0,0,1,0,1,0,0,0,0,0,0},//21湖北
			{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,1,0,1,0,1,0,0,1,0,0,0,0,0,0},//22安徽
			{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,0,1,1,0,0,0,0,0,0,0,0,0},//23江苏
			{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,0,0,0,0,0,0,0,0,0},//24上海
			{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,1,1,0,0,0,0,0},//25浙江
			{0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,1,1,0,1,0,0,0,0},//26湖南
			{0,0,1,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,0},//27广西
			{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,1,1,0,0,1,1,0,0,0,0},//28江西
			{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,0,1,0,0,0,0},//29福建
			{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,0,1,1,0,0},//30广东
			{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},//31香港
			{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0},//32澳门
			{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},//33海南
			{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}};//34台湾
	public static void main(String[] args) {
		Polygon[] p = new Polygon[34];  //将多变形封装在类中
		for(int i=0;i<34;i++){
			p[i] = new Polygon();
			p[i].npoints = p_x[i].length;
			p[i].xpoints = p_x[i];
			p[i].ypoints = p_y[i];
		}
		Frame frame = new Frame();
		frame.setLayout(null);
		frame.setBounds(300, 150, 800, 500);
		frame.setTitle("Print Map");
		frame.setResizable(false);
		frame.setBackground(new java.awt.Color(0,235,205));  //设置窗体的背景颜色
		MapColor mc = new MapColor(p);
		mc.setBounds(20, 40, 640, 440);
		mc.setBackground(Color.white);//设置地图的背景颜色
		frame.add(mc);
		Label label = new Label("time");
		label.setBounds(680, 50, 100, 20);
		label.setFont(new Font("宋体",Font.CENTER_BASELINE,18));
		frame.add(label);
		TextField text = new TextField();
		text.setBounds(680,80,100,30);
		text.setEditable(false);//不可写入
		frame.add(text);
		Checkbox cbx = new Checkbox(" Play",false);
		cbx.setFont(new  Font("宋体",Font.BOLD,18));
		cbx.setBounds(680, 130, 100, 40);
		frame.add(cbx);
		frame.setVisible(true);
		frame.addWindowListener(new MyWindowListener());
		Graphics g = mc.getGraphics();
		mc.paint(g);
		Button b1 = new Button("Result");
		b1.setBounds(680, 200, 100, 40);
		b1.addActionListener(new Monitor(mc,p,text,cbx,metrix));
		Button b3 = new Button("Resrtting");
		b3.setBounds(680, 290, 100, 40);
		b3.addActionListener(new Monitor(mc,p,text,cbx,metrix));
		frame.add(b1);
		frame.add(b3);
	}

}
class MapColor extends Canvas{
	/**
	 * 定义绘制多边形框和填充多边形
	 */
	private static final long serialVersionUID = 1489131206467420795L;
	private Color[] c = {Color.yellow,Color.pink,Color.green,Color.orange,Color.white};//定义填充颜色
	private Polygon[] p;
	public MapColor(Polygon[] p){
		this.p = p;
	}
	public void paint(Graphics g){   //绘制出所有多边形
		g.setColor(Color.black);
		for(int i=0;i<34;i++)
			g.drawPolygon(p[i]);
	}
	public void fillColor(Graphics g,int i,int j){ //给指定的多边形填充指定颜色
		g.setColor(c[j]);
		g.fillPolygon(p[i]);
	}
}

//窗口监听事件
class MyWindowListener implements WindowListener{
	public void windowClosing(WindowEvent e){
		((Frame)e.getComponent()).dispose();
		System.exit(0);
	}
	public void windowActivated(WindowEvent e){}
	public void windowClosed(WindowEvent e){}
	public void windowDeactivated(WindowEvent e){}
	public void windowDeiconified(WindowEvent e){}
	public void windowIconified(WindowEvent e){}
	public void windowOpened(WindowEvent e){}

}
//监听器
class Monitor implements ActionListener{
	private MapColor mc;
	private Polygon[] p;
	private TextField text;
	private Checkbox cbx;
	private int[][] metrix;
	public Monitor(MapColor mc,Polygon[] p,TextField text,Checkbox cbx,int[][] metrix){
		this.mc=mc;
		this.p=p;
		this.text=text;
		this.cbx=cbx;
		this.metrix=metrix;
	}
	public void actionPerformed(ActionEvent event){
		Object obj = event.getSource();
		Button btn = (Button)obj;
		if(btn.getLabel().equals("Result")){
			Map1 de = new Map1(mc,p,cbx,metrix);
			long startTime=System.currentTimeMillis();   //获取开始时间
			de.backtrack();
			long endTime=System.currentTimeMillis(); //获取结束时间
			text.setText((endTime-startTime)+"ms");
		}

		else{
			Map1 de = new Map1(mc,p,cbx,metrix);
			de.resetMap();
			text.setText(null);
			cbx.setState(false);
		}
	}
}

【算法分析与设计报告】快递终端送货配送系统、基因序列比较、地图染色、文章查重系统、果园篱笆问题（附源码）

一、快递终端送货分配问题

问题描述

1.1 问题一

1.1.1 问题一解决问题所用方法及基本思路

1.1.2 算法描述

1.1.3 算法的时间空间复杂度分析

1.1.4 算法实例

1.1.5 代码

1.2 问题二

1.2.1 解决问题所用的方法及基本思路

1.2.2 算法描述

1.2.3 算法的时间空间复杂度分析

1.2.4算法实例

1.2.5 代码

1.3问题三

1.3.1解决问题所用的方法及基本思路

1.3.2解决问题所用的方法及基本思路

1.3.3算法的时间空间复杂度分析

1.3.4算法实例

1.3.5 代码

1.4问题四

1.4.1解决问题所用的方法及基本思路

1.4.2算法描述

1.4.3算法的时间空间复杂度分析

1.4.4算法实例

1.5提出的问题及解决方法

二、文章查重系统

2.1 问题描述

1.2 解决问题所用的方法及基本思路

1.3 采用数据结构描述

1.4 算法描述

1.5 算法时间空间复杂度分析

1.6 代码

三、果园篱笆问题

3.1 问题描述

3.2 解决问题所用的方法及基本思路

3.3 采用的数据结构描述

3.4 算法描述

3.5 算法的时间空间复杂度分析

3.6 代码

四、基因序列比较

4.1 问题描述

4.2 解决问题所用的方法及基本思路

4.3 算法描述

4.4 算法时间空间复杂度分析

4.5 算法实例

4.6 代码

五、地图着色问题

5.1 问题描述

5.2 解决问题所用的方法及基本思路

5.3 算法描述

5.4 算法的时间空间复杂度分析

5.5 算法实例

5.6 代码

你可能感兴趣的:(算法,数据结构,算法,贪心算法,数据结构,动态规划)