【剑指offer】数据结构——树
目录
- 数据结构——树
-
- 直接解
-
- 【剑指offer】07. 重建二叉树
- 【剑指offer】08. 二叉树的下一个结点
- 【剑指offer】26. 树的子结构
- 【剑指offer】27. 二叉树的镜像
- 【剑指offer】28. 对称的二叉树
- 【剑指offer】32.1 从上到下打印二叉树
- 【剑指offer】32.2 从上到下打印二叉树2
- 【剑指offer】32.3 从上到下打印二叉树3 / 按之字形顺序打印二叉树
- 【剑指offer】34. 二叉树中和为某一值的路径
- 【剑指offer】37. 序列化二叉树
- 【剑指offer】55. 二叉树的深度
- 【剑指offer】68.2 二叉树的最近公共祖先
- 特殊解——二叉搜索树(BST)
-
- 【剑指offer】33. 二叉搜索树的后序遍历序列
- 【剑指offer】36. 二叉搜索树与双向链表
- 【剑指offer】54. 二叉搜索树的第k大节点
- 【剑指offer】68. 二叉搜索树的最近公共祖先
- 特殊解——二叉平衡树(AVL)
-
- 【剑指offer】55.2 平衡二叉树
数据结构——树
直接解
【剑指offer】07. 重建二叉树
题目描述
// 输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。
// 假设输入的前
// 序遍历和中序遍历的结果中都不含重复的数字。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
题解
// 时间复杂度: 2 ms , 在所有 Java 提交中击败了 97.96% 的用户
// 空间复杂度:38.5 MB, 在所有 Java 提交中击败了 94.78% 的用户
class Solution {
// 初始化一个hashmap
private Map indexForInOrders = new HashMap<>();
public TreeNode buildTree(int[] preorder, int[] inorder) {
// for循环遍历中序表,将中序表的值(key)和索引(value)存入hashmap
for (int i = 0; i < inorder.length; i++)
indexForInOrders.put(inorder[i], i);
// 调用递归函数,传入:
// 前序表,前序表左索引0,前序表右索引length - 1,中序表左索引0
return buildTree(preorder, 0, preorder.length - 1, 0);
}
// 定义递归函数
private TreeNode buildTree(int[] pre, int preL, int preR, int inL) {
// 若前序表左索引大于有索引,返回null
if (preL > preR)
return null;
// 取前序表左索引遍历值作为节点值
TreeNode root = new TreeNode(pre[preL]);
// 找到节点值在中序表的对应相同值(在中序表的)索引
int inIndex = indexForInOrders.get(root.val);
// 取节点值在中序表的索引,减去节点值在前序表的索引 / 中序表左索引,得到左子树的
// 规模(左子树节点数)
int leftTreeSize = inIndex - inL;
// 构建左子树,调用递归函数,传入:
// 前序表,前序表左索引右移,新前序表右索引=前序表左索引+左子树规模
// 中序表左索引
root.left = buildTree(pre, preL + 1, preL + leftTreeSize, inL);
// 构建右子树,调用递归函数,传入:
// 新前序表左索引=前序表左索引+左子树规模+1(因为要到右子树位置遍历),
// 前序表右索引,新中序表左索引=中序表左索引+左子树规模+1
root.right = buildTree(pre, preL + leftTreeSize + 1, preR, inL + leftTreeSize + 1);
// 返回树
return root;
}
}
class Solution {
public Map inOrderIndex = new HashMap<>();
public TreeNode buildTree(int[] preorder, int[] inorder) {
if (preorder.length == 0 || inorder.length == 0)
return null;
for (int i = 0; i < inorder.length; i++)
inOrderIndex.put(inorder[i], i);
return buildTree(preorder, 0, preorder.length - 1, 0);
}
private TreeNode buildTree(int[] pre, int preL, int preR, int inL) {
if (preL > preR)
return null;
TreeNode root = new TreeNode(pre[preL]);
int inIndex = inOrderIndex.get(pre[preL]);
int leftTreeSize = inIndex - inL;
root.left = buildTree(pre, preL + 1, preL + leftTreeSize, inL);
root.right = buildTree(pre, preL + leftTreeSize + 1, preR, inL + leftTreeSize + 1);
return root;
}
}
// 时间复杂度: 13 ms , 在所有 Java 提交中击败了 20.86% 的用户
// 空间复杂度:38.6 MB , 在所有 Java 提交中击败了 92.52% 的用户
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
if (preorder == null || inorder == null || preorder.length <= 0 || inorder.length <= 0) {
return null;
}
// 调用递归方法
TreeNode root = reConstruct(preorder, 0, preorder.length-1, inorder, 0, inorder.length-1);
return root;
}
// 定义递归方法:
// 初始传入:前序结果表,前序表遍历头索引,前序表遍历尾索引
// 中序结果表,中序表遍历头索引,中序表遍历尾索引
public TreeNode reConstruct(int[] pre, int startpre, int endpre, int[] in, int startin, int endin) {
// 如果中序表头索引大于中序表尾索引,
// 或前序表前索引大于前序表尾索引,填null
if (startin > endin || startpre > endpre) {
return null;
}
// 使用前序表头索引遍历数值,赋值结点数值
//(前序表第一个数为根节点)
TreeNode root = new TreeNode(pre[startpre]); // startpre遍历前序遍历结果表pre
// 每调用一次递归方法,就对中序表做一次for循环遍历,
// 如果找出前序表头索引遍历数,与中序表遍历数的相同对应数in[i]
// 则再次调用递归方法
// 左子树构建时,中序表头索引保持不变,中序表尾索引每递归一次则左移一次
// 缩小for循环搜索范围
// 右子树构建时,中序表尾索引保持不变,中序表头索引每递归一次则右移一次,
// 缩小for循环搜索范围
for (int i = startin; i <= endin; i++) {
// 若前序表头索引数等于中序表当前遍历元素,执行:
// (从前序表第一个数(根节点),可以找到中序表的根节点)
// (之后,前序表头索引将遍历到左子树元素,可以找到
// 中序表中的左子树元素)
if (pre[startpre] == in[i]) {
// System.out.print("startpre: ");System.out.print(startpre);
// System.out.print(" endpre: ");System.out.print(endpre);
// System.out.print(" startin: ");System.out.print(startin);
// System.out.print(" endin: ");System.out.println(endin);
// 左子树开始递归,构建左子树,传入:
// 1.前序表,2.前序表头索引右移一位,
// 3.新前序表尾索引 = 前序表尾索引-中序表尾索引+i,
// (i为上一次找到的前序表和中序表的相同对应数索引,
// 新前序表尾索引第一次会被赋值为根节点在中序表的位置。
// 之后直到左子树构建完,新前序表尾索引的值都不会变)
// 4.中序表,5.中序表头索引,
// 6.新中序表尾索引 = i-1(左子树,原i位置左移)
root.left = reConstruct(pre, startpre+1, endpre-endin+i, in, startin, i-1);
// 左子树构建完
// 右子树开始递归,传入:
// 1.前序表,2.新前序表头索引=前序表头索引-中序表头索引+i+1
// 3.前序表尾索引,
// 4.中序表,5.新中序表头索引为i+1(右子树,原i位置右移)
// 6.中序表尾索引
root.right = reConstruct(pre, startpre+i-startin+1, endpre, in, i+1, endin);
}
}
return root;
}
}
【剑指offer】08. 二叉树的下一个结点
题目描述
// 08. 二叉树的下一个结点
// 给定一个二叉树和其中的一个结点,请找出中序遍
// 历顺序的下一个结点并且返回。注意,树中的结点不仅包
// 含左右子结点,同时包含指向父结点的指针。
题解
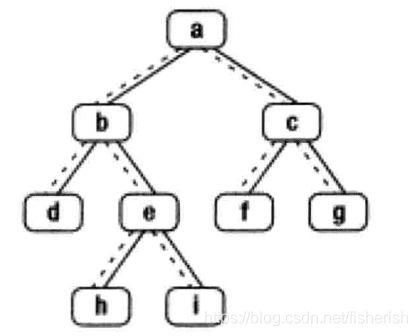
// 根据中序遍历的规则(先递归左子树取左结点,取根结点,后递归右子树取右结点),
// 我们可以倒过来讨论以下情况:
// 1,如果结点(a,b,c,e)有右子树(不管有没有左子树),
// 直接按照中序遍历规则在右子树找下一个结点
// 2,如果结点没有右子树,分两种情况:
// 一:如果结点回溯后发现自己是父结点的左子树,则下一结点就是父结点
// 二,如果结点回溯后发现自己是父结点的右子树,则继续回溯,并重新检查一 二
/*
public class TreeLinkNode {
int val;
TreeLinkNode left = null;
TreeLinkNode right = null;
TreeLinkNode next = null;
TreeLinkNode(int val) {
this.val = val;
}
}
*/
// 时间复杂度: 16ms 运行时间
// 空间复杂度:9868KB 占用内存
public class Solution {
public TreeLinkNode GetNext(TreeLinkNode pNode) {
if (pNode == null)
return null;
// 如果有右子树
if (pNode.right != null) {
TreeLinkNode node = pNode.right; // 进入右子树结点
while (node.left != null) { // 找有没有左子树
node = node.left; // 如果有左子树,找出最左的结点
}
return node; // 有左子树返回最左的结点,没左子树直接返回
}
// 如果没有右子树
else {
while (pNode.next != null) { // 回溯
TreeLinkNode node = pNode.next; // 先行取父结点
// 若当前结点为父结点的左子树结点
if (node.left == pNode)
return node; // 直接返回父结点
pNode = pNode.next; // 结点回溯
}
}
return null; // 回溯无法找出关系,说明是结点已经处于整棵树最右
}
}
【剑指offer】26. 树的子结构
题目描述
// 26. 树的子结构
// 力扣
// 输入两棵二叉树A和B,判断B是不是A的子结构。(约定
// 空树不是任意一个树的子结构)
// B是A的子结构, 即 A中有出现和B相同的结构和节点值。
// 牛客
// 输入两棵二叉树A,B,判断B是不是A的子结构。(ps:我们
// 约定空树不是任意一个树的子结构)
题解
// 力扣
// 执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
// 内存消耗:39.9 MB, 在所有 Java 提交中击败了95.56%的用户
class Solution {
// 解题函数:作用是寻找B树是否是A树的子树(A树是否包含B)
public boolean isSubStructure(TreeNode A, TreeNode B) {
if (A == null || B == null) // 如果其中一个为null,直接返回false
return false;
boolean res = false;
// 如果A和B根结点相同,调用recur函数判断之后的遍历AB两树是否相同
if (A.val == B.val)
res = recur(A, B); // 遍历结果返回为res
if (!res) // 如果没找出子树结构
// 递归调用解题函数,输入A.left:判断A左子树是否包含B
res = isSubStructure(A.left, B);
if (!res)
// 递归调用解题函数,输入A.right:判断A右子树是否包含B
res = isSubStructure(A.right, B);
return res;
}
// 前序遍历的判断函数:从当前输入结点A和B开始,以前序遍历顺序
// 逐节点判断A数是不是包含B树,其中:
// 1.B树如果被遍历完了,说明A树此前遍历的所有结点和B相同,B树为A子树
// 2.如果A树被遍历完了,直接返回false,B树不可能是A子树
// 3.如果出现遍历节点不相等,返回false。
// 返回:recur(A.left,B.left) && recur(A.right, B.right);
// 也就是先遍历完当前结点,再左树,再右树,此为遵循了前序遍历的顺序。
public boolean recur(TreeNode A, TreeNode B) {
if (B == null) return true;
if (A == null) return false;
if (A.val != B.val) return false;
// 能到达return语句,说明满足A.val==B.val了
return recur(A.left, B.left) && recur(A.right, B.right);
}
}
// 力扣
// 意思跟上面的是一样的,只是写法不同。
// 执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
// 内存消耗:40.2 MB, 在所有 Java 提交中击败了67.07%的用户
class Solution {
public boolean isSubStructure(TreeNode A, TreeNode B) {
if (A == null || B == null) {
return false;
}
return (recur(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B))
}
private boolean recur(TreeNode A, TreeNode B) {
if (B == null) return true;
if (A == null) return false;
if (A.val != B.val) return false;
return recur(A.left, B.left) && recur(A.right, B.right);
}
}
// 牛客
// 运行时间:16ms
// 占用内存:9804k
public class Solution {
public boolean HasSubtree(TreeNode root1,TreeNode root2) {
if (root1 == null || root2 == null)
return false;
boolean res = false;
if (root1.val == root2.val)
res = recur(root1, root2);
if (!res)
res = HasSubtree(root1.left, root2);
if (!res)
res = HasSubtree(root1.right, root2);
return res;
}
private boolean recur(TreeNode A, TreeNode B) {
if (B == null)
return true;
if (A == null)
return false;
if (A.val != B.val)
return false;
return recur(A.left, B.left) && recur(A.right, B.right);
}
}
// 牛客
// 运行时间:11ms
// 占用内存:9760k
public class Solution {
public boolean HasSubtree(TreeNode root1,TreeNode root2) {
if (root1 == null || root2 == null)
return false;
return (recur(root1, root2) || HasSubtree(root1.left, root2) || HasSubtree(root1.right, root2));
}
private boolean recur(TreeNode A, TreeNode B) {
if (B == null)
return true;
if (A == null)
return false;
if (A.val != B.val)
return false;
return recur(A.left, B.left) && recur(A.right, B.right);
}
}
【剑指offer】27. 二叉树的镜像
题目描述
![]()
![]()
// 力扣
// 请完成一个函数,输入一个二叉树,该函数输出它的镜像。
// 牛客
// 操作给定的二叉树,将其变换为源二叉树的镜像。
题解
// 递归一定要按照函数的语义来递归,往往不需要知道递归细节
// 递归到最后总是会需要解决问题的基本单元,在这道题目中,
// 问题的基本单元就是交换一个根结点的左结点(假设是叶结点吧)和右结点
// 力扣
// 执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
// 内存消耗:35.7 MB, 在所有 Java 提交中击败了82.58%的用户
class Solution {
// 解题函数:使输入二叉树root镜像翻转
// 遍历按照前序遍历的顺序,先对当前结点使用swap,
// 然后在左子树递归镜像翻转函数mirrorTree,
// 最后在右子树递归镜像翻转函数mirrorTree
public TreeNode mirrorTree(TreeNode root) {
if (root == null)
return null;
swap(root); //
mirrorTree(root.left);
mirrorTree(root.right);
return root;
}
// 交换函数:仅对当前根结点A的左子树与右子树交换一次位置
private TreeNode swap(TreeNode A) {
TreeNode temp = A.left;
A.left = A.right;
A.right = temp;
return A;
}
}
// 牛客
// 运行时间:15ms
// 占用内存:9836k
public class Solution {
public void Mirror(TreeNode root) {
if (root == null)
return;
root = swap(root);
Mirror(root.left);
Mirror(root.right);
}
private TreeNode swap(TreeNode A) {
TreeNode temp = A.left;
A.left = A.right;
A.right = temp;
return A;
}
}
【剑指offer】28. 对称的二叉树
// 28. 对称的二叉树
// 请实现一个函数,用来判断一棵二叉树是不是对称的。如果一
// 棵二叉树和它的镜像一样,那么它是对称的。
// 例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
// 1
// / \
// 2 2
// / \ / \
// 3 4 4 3
// 但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
// 1
// / \
// 2 2
// \ \
// 3 3
题解
// 还记得在《26. 树的子结构》这道题中,我们需要找到B数是不是A的子树,
// 需要逐个结点遍历B树判断是不是和A相同。本题有异曲同工之妙,
// 只是需要遍历的树变成了自己本身,给定一个树root,
// 我们需要同时遍历root的左树和右树,在左树遍历点和右树遍历点中
// 我们需要判断:
// 1.左子树遍历点和右子树遍历点是不是相等,
// 2.左子树的左子树点与右子树的右子树点是不是相等,
// 3.左子树的右子树点与右子树的左子树点是不是相等。
// 力扣
// 执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
// 内存消耗:36.4 MB, 在所有 Java 提交中击败了74.58%的用户
class Solution {
public boolean isSymmetric(TreeNode root) {
if (root == null)
return true;
return recur(root, root);
}
private boolean recur(TreeNode root1, TreeNode root2) {
if (root1 == null && root2 == null)
return true;
if (root1 == null || root2 == null)
return false;
if (root2.val != root1.val)
return false;
return (recur(root1.left, root2.right) && recur(root1.right, root2.left));
}
}
// 牛客
// 运行时间:11ms
// 占用内存:9652k
public class Solution {
boolean isSymmetrical(TreeNode pRoot) {
if (pRoot == null)
return true;
return recur(pRoot, pRoot);
}
private boolean recur(TreeNode root1, TreeNode root2) {
if (root1 == null && root2 == null)
return true;
if (root1 == null || root2 == null)
return false;
if (root1.val != root2.val)
return false;
return recur(root1.left, root2.right) && recur(root1.right, root2.left);
}
}
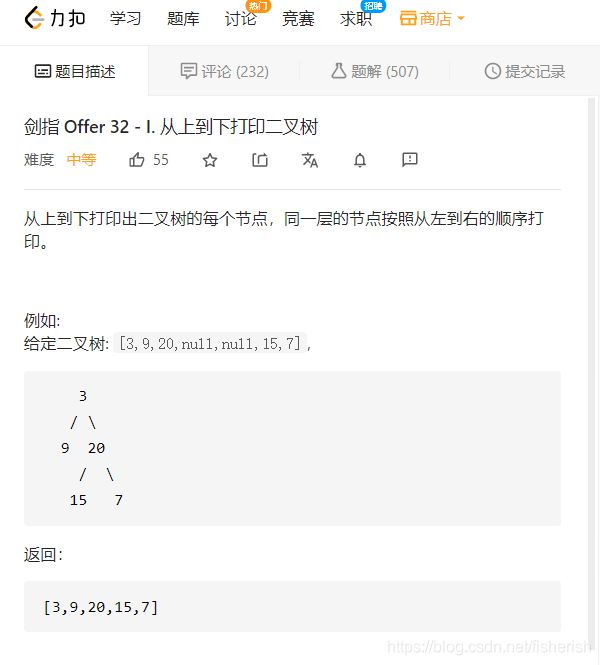
【剑指offer】32.1 从上到下打印二叉树
题目描述
// 力扣
// 从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。
// 牛客
// 从上往下打印出二叉树的每个节点,同层节点从左至右打印。
题解
就是数的层序遍历,只是需要把遍历的结点值保存
层序遍历可以见:
https://www.runoob.com/data-structures/b
// 力扣
// 执行用时:1 ms, 在所有 Java 提交中击败了99.78%的用户
// 内存消耗:38.3 MB, 在所有 Java 提交中击败了94.10%的用户
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
import java.util.Queue;
class Solution {
public int[] levelOrder(TreeNode root) {
if (root == null)
return new int[0]; // 如果root为空直接返回空列表
int size = 0; // 最终结果列表需要记录size来构建
// 第一个队列q(用链表模拟队列),用于层序遍历
LinkedList q = new LinkedList<>();
// 第二个队列q_val,用于保存结点的值,待会放进列表中
Queue q_val = new LinkedList();
q.offer(root); // 头结点入队q(add也可以,只是offer不抛出异常)
// 当q为空,即q中所有结点都出队,说明root的所有结点都已经遍历过
while (!q.isEmpty()) {
TreeNode node = q.remove(); // 把放进q的结点出队,记为node
size++;
q_val.add(node.val); // 结点node的值存入q_val
if (node.left != null) // 出队结点node如果有左结点
q.add(node.left); // node左结点入队q
if (node.right != null) // 出队结点node如果有右结点
q.add(node.right); // node右结点入队q
}
int[] res = saveToList(size, q_val); // 把q_val中的值存入列表res
return res;
}
private int[] saveToList(int size, Queue q_val) {
int[] res = new int[size];
for (int i = 0; i < size; i++) {
res[i] = q_val.poll();
}
return res;
}
}
// 力扣
// 执行用时:1 ms, 在所有 Java 提交中击败了99.74%的用户
// 内存消耗:38.4 MB, 在所有 Java 提交中击败了80.21%的用户
import java.util.Queue;
class Solution {
public int[] levelOrder(TreeNode root) {
if (root == null)
return new int[0];
TreeNode cur = root;
Queue q = new LinkedList<>();
Queue q_val = new LinkedList<>();
q.add(cur);
while (!q.isEmpty()) {
TreeNode node = q.remove();
q_val.add(node.val);
if (node.left != null)
q.add(node.left);
if (node.right != null)
q.add(node.right);
}
int[] res = saveToList(q_val.size(), q_val);
return res;
}
private int[] saveToList(int size, Queue q_val) {
int[] res = new int[size];
for (int i = 0; i < size; i++) {
res[i] = q_val.poll();
}
return res;
}
}
// 牛客
// 运行时间:12ms
// 占用内存:9660k
import java.util.ArrayList;
import java.util.LinkedList;
public class Solution {
public ArrayList PrintFromTopToBottom(TreeNode root) {
ArrayList res = new ArrayList<>();
if (root == null)
return res;
LinkedList q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
TreeNode node = q.remove();
res.add(node.val);
if (node.left != null)
q.add(node.left);
if (node.right != null) {
q.add(node.right);
}
}
return res;
}
}
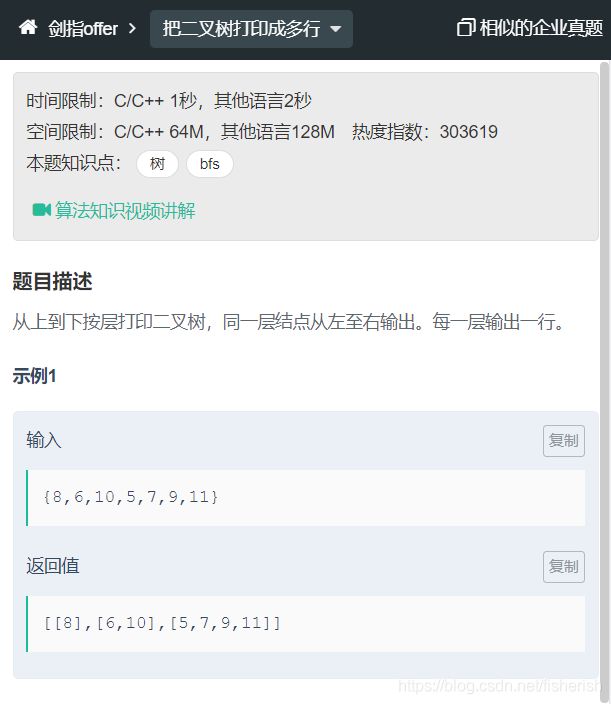
【剑指offer】32.2 从上到下打印二叉树2
题目描述
// 力扣
// 从上到下按层打印二叉树,同一层的节点按从左到右
// 的顺序打印,每一层打印到一行。
// 牛客
// 从上到下按层打印二叉树,同一层结点从左至右输出。每一层输出一行。
题解
// 本题最重要是需要将不同层之间分离出来
// 因此不能像《32.1 从上到下打印二叉树》一样每次结点出队就直接左右子树入队
队列分割 ///
// 队列分割,不是最好的方法,但是比较好理解
// 创建两个队列,一个队列q_cur用于上一层的结点出队,
// 另一个队列q_next用于保存下一层的结点。q_cur全部出队,则
// q_next结点给q_cur,重复操作。
// 力扣
// 执行用时:1 ms, 在所有 Java 提交中击败了92.86%的用户
// 内存消耗:38.4 MB, 在所有 Java 提交中击败了88.06%的用户
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
import java.util.ArrayList;
class Solution {
public List> levelOrder(TreeNode root) {
// 注意这里的初始化数据类型直接new ArrayList>()就行
List> res = new ArrayList>();
if (root == null)
return res;
// 构建两个队列,队列用链表模拟,
// q_cur用于存当前层的结点遍历,q_next用于下一层结点的存储
LinkedList q_cur = new LinkedList();
LinkedList q_next = new LinkedList();
q_next.offer(root); // 先根结点存入q_next
// 如果下一层结点全部遍历完(没有子树),循环结束
while (!q_next.isEmpty()) {
// System.out.println(res.toString());
// 将q_next结点全部存入q_cur
while (!q_next.isEmpty()) {
TreeNode node = q_next.remove();
q_cur.add(node);
}
// level用于存储当前层的结点元素,每次大循环就new一个level
ArrayList level = new ArrayList();
// 将当前层q_cur的结点全部出队,出队结点元素存入level
// 将出队结点的左右子结点全部存入q_next(下一层)
// 如果当前层的结点全部出队,循环结束
while (!q_cur.isEmpty()) {
TreeNode node = q_cur.remove();
level.add(node.val);
if (node.left != null)
q_next.add(node.left);
if (node.right != null)
q_next.add(node.right);
}
// 将存好当前层元素的列表level存入res
res.add(level);
}
return res;
}
}
// 牛客
// 运行时间:24ms
// 占用内存:10000k
import java.util.ArrayList;
import java.util.LinkedList;
public class Solution {
ArrayList> Print(TreeNode pRoot) {
ArrayList> res = new ArrayList>;
LinkedList q_cur = new LinkedList<>();
LinkedList q_next = new LinkedList<>();
q_next.offer(pRoot);
while (!q_next.isEmpty()) {
while (!q_next.isEmpty()) {
TreeNode node = q_next.remove();
q_cur.add(node);
}
ArrayList level = new ArrayList<>();
while (!q_cur.isEmpty()) {
TreeNode node = q_cur.remove();
level.add(node.val);
if (node.left != null)
q_next.add(node.left);
if (node.right != null)
q_next.add(node.right);
}
res.add(level);
}
return res;
}
}
计数分割
// 比较巧妙的方法
// 设置一个计数位level_count,在根结点出队,放子结点入队后,队伍里的
// 长度即为子结点一层的结点个数。
// 遍历一个结点,计数位减1,计数位耗尽表示当前层遍历完毕。
// 力扣
// 执行用时:1 ms, 在所有 Java 提交中击败了92.86%的用户
// 内存消耗:38.5 MB, 在所有 Java 提交中击败了85.92%的用户
import java.util.ArrayList;
class Solution {
public List> levelOrder(TreeNode root) {
List> res = new ArrayList>();
if (root == null)
return res;
int level_count = 0;
LinkedList q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
ArrayList level = new ArrayList<>();
level_count = q.size();
while (level_count > 0) {
TreeNode node = q.remove();
level.add(node.val);
if (node.left != null)
q.add(node.left);
if (node.right != null)
q.add(node.right);
level_count--;
}
res.add(level);
// System.out.println(res.toString());
}
return res;
}
}
// 牛客
// 运行时间:17ms
// 占用内存:9956k
import java.util.ArrayList;
import java.util.LinkedList;
public class Solution {
ArrayList> Print(TreeNode pRoot) {
ArrayList> res = new ArrayList>();
if (pRoot == null)
return res;
int level_count = 1;
LinkedList q = new LinkedList<>();
q.offer(pRoot);
while (!q.isEmpty()) {
ArrayList level = new ArrayList<>();
level_count = q.size();
while (level_count > 0) {
TreeNode node = q.remove();
level.add(node.val);
if (node.left != null)
q.add(node.left);
if (node.right != null)
q.add(node.right);
level_count--;
}
res.add(level);
}
return res;
}
}
【剑指offer】32.3 从上到下打印二叉树3 / 按之字形顺序打印二叉树
题目描述
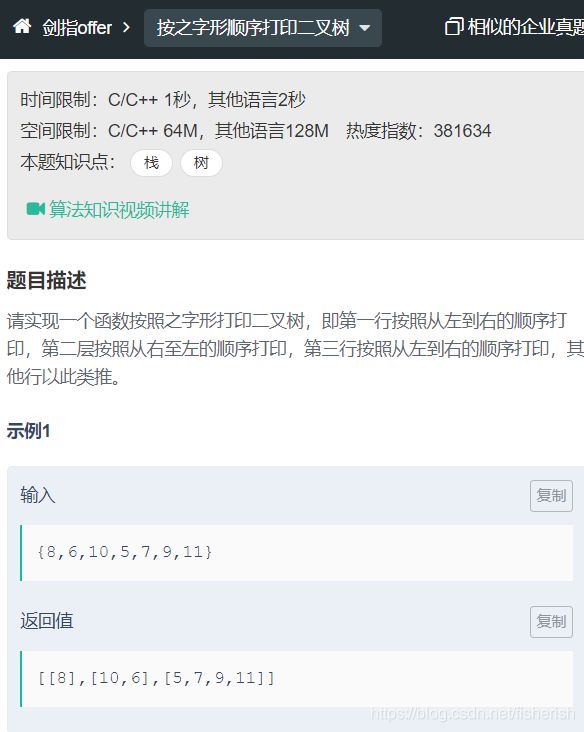
// 32.3 从上到下打印二叉树3 / 按之字形顺序打印二叉树
// 力扣
// 请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右
// 的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到
// 右的顺序打印,其他行以此类推。
// 牛客
// 请实现一个函数按照之字形打印二叉树,即第一行按照从左到右的顺序打
// 印,第二层按照从右至左的顺序打印,第三行按照从左到右的顺序打印,
// 其他行以此类推。
题解
/ 列表翻转法 /
// 直接在《32.2 从上到下打印二叉树2》基础上改一改就行
// 新增方向判断符,判断这一层的打印方向。需要反方向则直接反转列表。
// 牛客
// 运行时间:16ms
// 占用内存:9904k
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Collections;
public class Solution {
public ArrayList> Print(TreeNode pRoot) {
ArrayList> res = new ArrayList>();
if (pRoot == null)
return res;
LinkedList q = new LinkedList<>();
int level_count = 0;
boolean left_dic = false; // 下一层的方向(从左到右还是从右到左)
q.offer(pRoot);
while (!q.isEmpty()) {
ArrayList level = new ArrayList<>();
level_count = q.size();
while (level_count > 0) {
TreeNode node = q.remove();
level.add(node.val);
if (node.left != null)
q.add(node.left);
if (node.right != null)
q.add(node.right);
level_count--;
if (level_count <= 0)
left_dic = !left_dic;
}
if (!left_dic)
Collections.reverse(level);
res.add(level);
}
return res;
}
}
// 力扣
// 执行用时:2 ms, 在所有 Java 提交中击败了27.31%的用户
// 内存消耗:38.4 MB, 在所有 Java 提交中击败了94.68%的用户
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Collections;
class Solution {
public List> levelOrder(TreeNode root) {
List> res = new ArrayList<>();
if (root == null)
return res;
LinkedList q = new LinkedList<>();
int level_count = 0;
boolean left_dic = false;
q.offer(root);
while (!q.isEmpty()) {
ArrayList level = new ArrayList<>();
level_count = q.size();
while (level_count > 0) {
TreeNode node = q.remove();
level.add(node.val);
if (node.left != null)
q.add(node.left);
if (node.right != null)
q.add(node.right);
level_count--;
if (level_count <= 0)
left_dic = !left_dic;
}
if (!left_dic)
Collections.reverse(level);
res.add(level);
}
return res;
}
}
// 双端队列法 ///
// 根据方向判定符left_dic,在双端队列(其他数据结构也行)中使用头部入队或者是尾部入队,
// 其他地方还是一样的套路。
// 力扣
// 执行用时:1 ms, 在所有 Java 提交中击败了99.76%的用户
// 内存消耗:38.9 MB, 在所有 Java 提交中击败了21.29%的用户
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Collections;
class Solution {
public List> levelOrder(TreeNode root) {
List> res = new ArrayList<>();
if (root == null)
return res;
LinkedList q = new LinkedList<>();
int level_count = 0;
boolean left_dic = false; // 下一层的方向(从左到右还是从右到左)
q.offer(root);
while (!q.isEmpty()) {
LinkedList level = new LinkedList<>();
level_count = q.size();
while (level_count > 0) {
TreeNode node = q.remove();
if (left_dic)
level.addFirst(node.val);
else
level.addLast(node.val);
if (node.left != null)
q.add(node.left);
if (node.right != null)
q.add(node.right);
level_count--;
if (level_count <= 0)
left_dic = !left_dic;
}
res.add(level);
}
return res;
}
}
// 牛客
// 跟力扣一样,只是返回的数据类型有区别
// 力扣的方法在牛客不能用,但是牛客的方法在力扣可以用
// 运行时间:16ms
// 占用内存:9996k
import java.util.ArrayList;
import java.util.LinkedList;
public class Solution {
public ArrayList> Print(TreeNode pRoot) {
ArrayList> res = new ArrayList<>();
if (pRoot == null)
return res;
LinkedList q = new LinkedList<>();
int level_count = 0;
boolean left_dic = false; // 下一层的方向(从左到右还是从右到左)
q.offer(pRoot);
while (!q.isEmpty()) {
ArrayList level = new ArrayList<>();
level_count = q.size();
while (level_count > 0) {
TreeNode node = q.remove();
if (left_dic)
level.add(0, node.val); // 如果是ArrayList就这样子操作
else
level.add(node.val);
if (node.left != null)
q.add(node.left);
if (node.right != null)
q.add(node.right);
level_count--;
if (level_count <= 0)
left_dic = !left_dic;
}
res.add(level);
}
return res;
}
}
【剑指offer】34. 二叉树中和为某一值的路径
题目描述
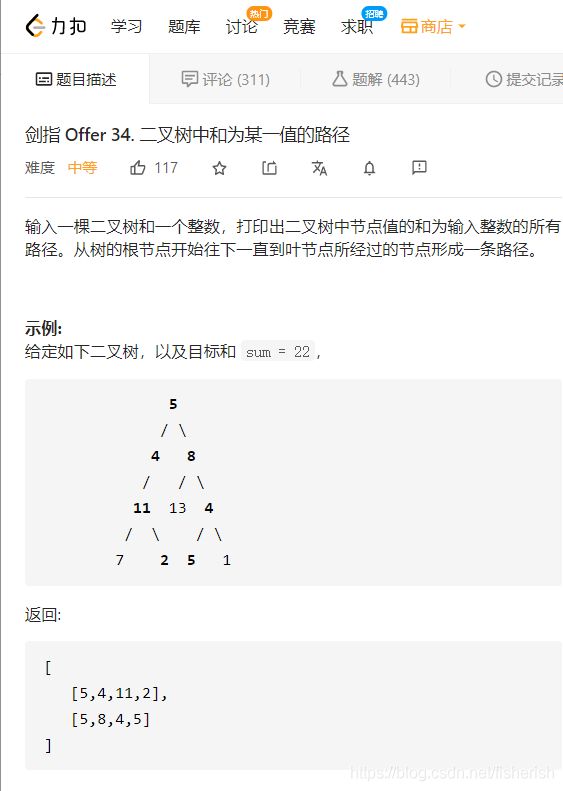
// 输入一棵二叉树和一个整数,打印出二叉树中节点值的和为输入整
// 数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点
// 形成一条路径。
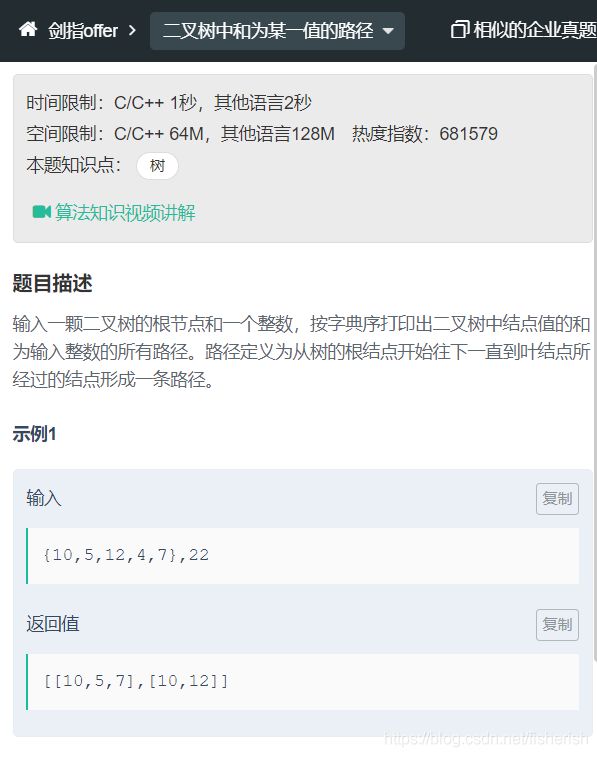
// 输入一颗二叉树的根节点和一个整数,按字典序打印出二叉树中结点值
// 的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到
// 叶结点所经过的结点形成一条路径。
题解
// 前序遍历,用数组path记录遍历元素,遍历到元素就存进去,回溯父结点就删掉元素。
// 遍历同时要记录遍历元素的和是否等于target(大于小于都没用),由于题目
// 的路径必须要从根节点到叶节点,如果记录的遍历元素之和与target相等,
// 还需要判断当前遍历结点是否是叶节点(没有左右子树)。
// 力扣
// 执行用时:1 ms, 在所有 Java 提交中击败了100.00%的用户
// 内存消耗:38.8 MB, 在所有 Java 提交中击败了55.26%的用户
class Solution {
List> res = new ArrayList<>(); // 答案保存组res
public List> pathSum(TreeNode root, int sum) {
ArrayList path = new ArrayList(); // 单条路径初始化
recur(root, sum, path); // 开始前序遍历
return res;
}
private void recur(TreeNode root, int target, ArrayList path) {
if (root == null) // 根据前序遍历,如果走到头了,return
return;
path.add(root.val); //当前遍历元素root.val存入路径数组path
// 令target减去遍历的每一个元素root.val(减为0说明当前路径之和为target)
target -= root.val;
// 如果路径之和为target,且路径重点是叶节点,把路径path保存入res
if ((target == 0) && (root.left == null) && (root.right == null))
// 这里必须重新new一下,否则只是将path对象加进了res
// path改变了res对象也会改变,重新new相当于复制了一个path,
// 对象已经不同了
res.add(new ArrayList<>(path));
else { // 否则,就按照前序遍历走下去
recur(root.left, target, path);
recur(root.right, target, path);
}
// 前序遍历回溯,将路径path的末尾点删掉表示路径回溯(到父结点
path.remove(path.size() - 1);
}
}
// 执行用时:1 ms, 在所有 Java 提交中击败了100.00%的用户
// 内存消耗:38.6 MB, 在所有 Java 提交中击败了75.51%的用户
class Solution {
List> res;
List temp;
public List> pathSum(TreeNode root, int target) {
this.res = new ArrayList<>();
this.temp = new ArrayList<>();
search(root, target);
return res;
}
private void search(TreeNode root, int target) {
if (root == null)
return;
target -= root.val;
temp.add(root.val);
if (root.left == null && root.right == null && target == 0) {
res.add(new ArrayList<>(temp));
}
search(root.left, target);
search(root.right, target);
temp.remove(temp.size() - 1);
return;
}
}
// 牛客
// 运行时间:14ms
// 占用内存:9840k
import java.util.ArrayList;
public class Solution {
ArrayList> res = new ArrayList<>();
public ArrayList> FindPath(TreeNode root,int target) {
ArrayList path = new ArrayList<>();
recur(root, target, path);
return res;
}
private void recur(TreeNode root, int target, ArrayList path) {
if (root == null)
return;
target -= root.val;
path.add(root.val);;
if ((target == 0) && (root.left == null) && (root.right == null))
res.add(new ArrayList<>(path));
else {
recur(root.left, target, path);
recur(root.right, target, path);
}
path.remove(path.size() - 1);
}
}
【剑指offer】37. 序列化二叉树
题目描述
// 37. 序列化二叉树
// 请实现两个函数,分别用来序列化和反序列化二叉树。
// 你可以将以下二叉树:
// 1
// / \
// 2 3
// / \
// 4 5
// 序列化为 "[1,2,3,null,null,4,5]"
// 牛客
// 请实现两个函数,分别用来序列化和反序列化二叉树
// 二叉树的序列化是指:把一棵二叉树按照某种遍历方式的结果以某种格
// 式保存为字符串,从而使得内存中建立
// 起来的二叉树可以持久保存。序列化可以基于先序、中序、后序、层序
// 的二叉树遍历方式来进行修改,序列化的结果是一个字符串,序列化时
// 通过 某种符号表示空节点(#),以 ! 表示一个结点值的结束(valu
// e!)。
// 二叉树的反序列化是指:根据某种遍历顺序得到的序列化字符串结果str
// ,重构二叉树。
// 例如,我们可以把一个只有根节点为1的二叉树序列化为"1,",然后通过自己
// 的函数来解析回这个二叉树
题解
// 这题很难啊,
// 序列化是为了能够完整地保存树的结构信息,这个信息最后可以为
// 反序列化而服务,即根据这个序列化信息完整的还原这个二叉树。
// 按照题意,序列化使用层序遍历的同时需要将null也保存下来。
// 力扣
// 执行用时:23 ms, 在所有 Java 提交中击败了62.32%的用户
// 内存消耗:40.7 MB, 在所有 Java 提交中击败了47.02%的用户
import java.util.LinkedList;
public class Codec {
// 序列化
public String serialize(TreeNode root) {
if (root == null) // 若树为null直接返回"[]"
return "[]";
// 创建StringBuilder用于存string结构信息
StringBuilder res = new StringBuilder();
// 创建层序遍历要用的队列(用LinkedList模拟)
LinkedList q = new LinkedList<>();
res.append("[");
q.add(root);
while(!q.isEmpty()) {
TreeNode node = q.remove(); // 结点出队即为node
// 如果遍历当前的node非空,将node.val和逗号","存入res
// 并将node的左右子结点入队(不管是不是null,因为null我们也要记录)
if (node != null) {
res.append(node.val + ",");
q.add(node.left);
q.add(node.right);
}
else
res.append("null,"); // 如果是null,把"null,"存入
}
// 存完res末尾会多一个逗号,删掉
res.deleteCharAt(res.length() - 1);
res.append("]");
// System.out.println(res.toString());
return res.toString(); // 转String
}
// 反序列化
public TreeNode deserialize(String data) {
if (data.equals("[]")) // 如果string是"[]",说明树是null
return null;
// 先掐头去尾把中括号"[]"去掉,然后将data中的字符按照逗号分隔
// 得到字符组vals
String[] vals = data.substring(1, data.length() - 1).split(",");
// parseInt将字符串参数解析为有符号的十进制数,即为结点值,
// 用结点值新建结点作为遍历的第一个点
TreeNode res = new TreeNode(Integer.parseInt(vals[0]));
// 初始化队列q,用于构建二叉树,构建过程类似层序遍历
LinkedList q = new LinkedList<>();
q.add(res);
int i = 1; // 遍历字符组vals的索引指针i
// 若q为空(vals中的有效结点遍历完),循环结束
while (!q.isEmpty()) {
TreeNode node = q.remove(); // 结点出队
// 如果vals[i]元素不是null
if (!vals[i].equals("null")) {
// 解析结点值新建结点,使node.left指向该结点
node.left = new TreeNode(Integer.parseInt(vals[i]));
q.add(node.left); // 入队
}
i++; // 指针右移
// 如果下一个vals[i]元素不是null
if (!vals[i].equals("null")) {
// 同上
node.right = new TreeNode(Integer.parseInt(vals[i]));
q.add(node.right);
}
i++; // 指针右移
}
return res; // 最后返回树
}
}
// 牛客
// 运行时间:18ms
// 占用内存:10032k
import java.util.LinkedList;
public class Solution {
String Serialize(TreeNode root) {
if (root == null)
return "[]";
StringBuilder res = new StringBuilder();
LinkedList q = new LinkedList<>();
res.append("[");
q.add(root);
while (!q.isEmpty()) {
TreeNode node = q.remove();
if (node != null) {
res.append(node.val + ",");
q.add(node.left);
q.add(node.right);
}
else
res.append("null,");
}
res.append("]");
return res.toString();
}
TreeNode Deserialize(String str) {
if (str.equals("[]"))
return null;
String[] vals = str.substring(1, str.length() - 1).split(",");
LinkedList q = new LinkedList<>();
TreeNode res = new TreeNode(Integer.parseInt(vals[0]));
q.add(res);
int i = 1;
while (!q.isEmpty()) {
TreeNode node = q.remove();
if (!vals[i].equals("null")) {
node.left = new TreeNode(Integer.parseInt(vals[i]));
q.add(node.left);
}
i++;
if (!vals[i].equals("null")) {
node.right = new TreeNode(Integer.parseInt(vals[i]));
q.add(node.right);
}
i++;
}
return res;
}
}
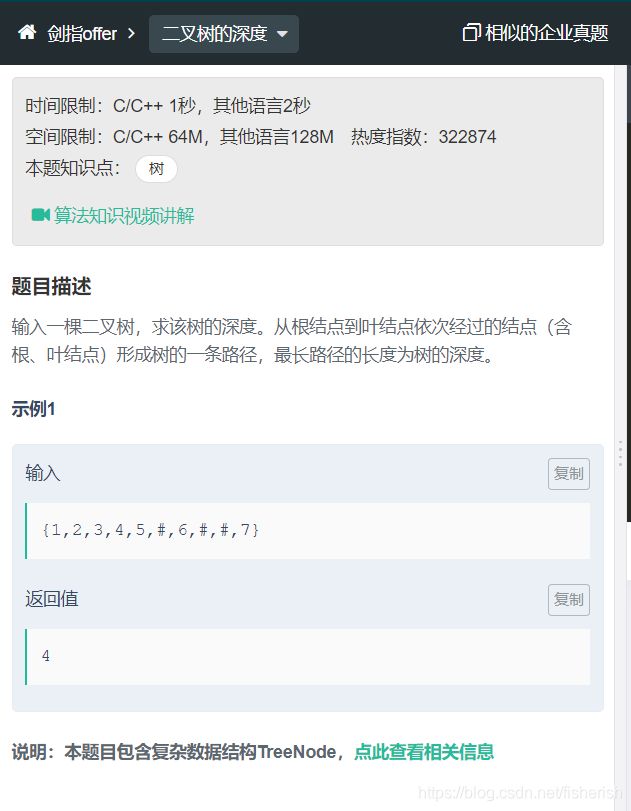
【剑指offer】55. 二叉树的深度
题目描述
// 55. 二叉树的深度
// 力扣
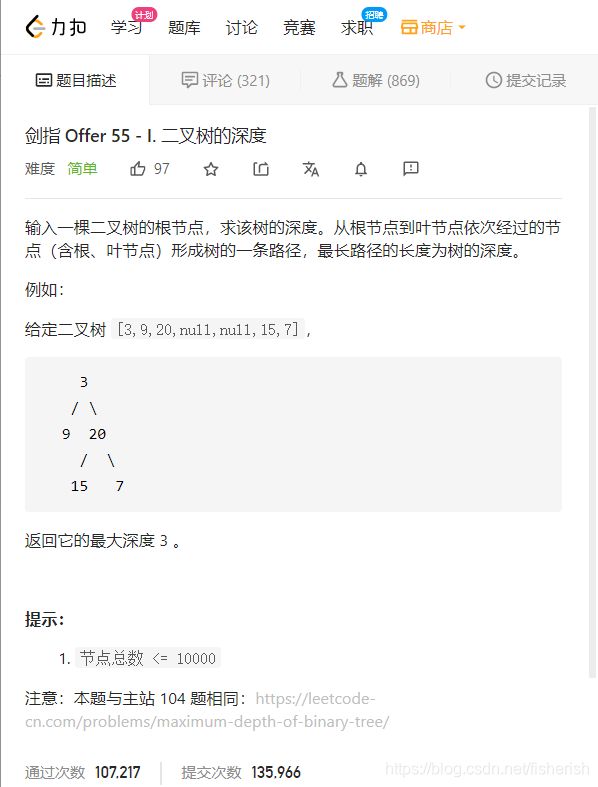
// 输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次
// 经过的节点(含根、叶节点)形成树的一条路径,最长路径的长度
// 为树的深度。
// 牛客
// 输入一棵二叉树,求该树的深度。从根结点到叶结点依次经过的结点(
// 含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。
题解
///
// 力扣
// 遍历树,从叶节点到末端返回0,除此之外经过结点就+1,取right和left较大
// 的一边累加,最终可以得到树深度。
// 执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
// 内存消耗:38.4 MB, 在所有 Java 提交中击败了54.31%的用户
class Solution {
public int maxDepth(TreeNode root) {
if (root == null)
return 0;
int left = maxDepth(root.left);
int right = maxDepth(root.right);
return (left > right) ? left + 1 : right + 1;
}
}
// 力扣
// 或者这样写
// 执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
// 内存消耗:38.4 MB, 在所有 Java 提交中击败了47.72%的用户
class Solution {
public int maxDepth(TreeNode root) {
return (root == null) ? 0 : 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
}
}
// 牛客
// 运行时间:10ms,超过90.74%用Java提交的代码
// 占用内存:9532KB,超过72.37%用Java提交的代码
public class Solution {
public int TreeDepth(TreeNode root) {
return (root == null) ? 0 : 1 + Math.max(TreeDepth(root.left), TreeDepth(root.right));
}
}
【剑指offer】68.2 二叉树的最近公共祖先
// 68.2 二叉搜索树的最近公共祖先
// 力扣
// 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
// 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,
// 最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度
// 尽可能大(一个节点也可以是它自己的祖先)。”
// 例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
题解
// 力扣
// 还记得《68. 二叉搜索树的最近公共祖先》,本题是68的一般情况,
// 因此可以本题的解可以用于68。
//
// 根据p和q的情况可以分成:
// 1.p和q不在同一个子树中,则公共祖先存在于p和q的父结点以上,且公共祖先
// 一定是p和q所在子树分支的根结点。
// 2.p在q的左/右子树中,公共祖先就是q,
// 3.q在p的左/右子树中,公共祖先就是p。
//
// 遍历节点为root,递归终止条件为当root==null,或遍历节点到了p,
// 或遍历节点到了q时,返回root。root==null,说明遍历到了尽头,没有遇到
// p和q。当遇到p和q时,再往深遍历是不可能遇到公共祖先的,直接返回root。
//
// 递归调用主函数,输入为遍历节点root的左子树root.left,得到节点left。
// 递归调用主函数,输入为遍历节点root的右子树root.right,得到节点right。
// 如此递归树的左右每一个节点,如果得到的left==null,返回right,
// 如果得到的right==null,返回left。最终主函数返回root。
//
// 执行用时:7 ms, 在所有 Java 提交中击败了100.00%的用户
// 内存消耗:39.9 MB, 在所有 Java 提交中击败了56.35%的用户
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || p == root || q == root)
return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left == null)
return right;
else if (right == null)
return left;
return root;
}
}
特殊解——二叉搜索树(BST)
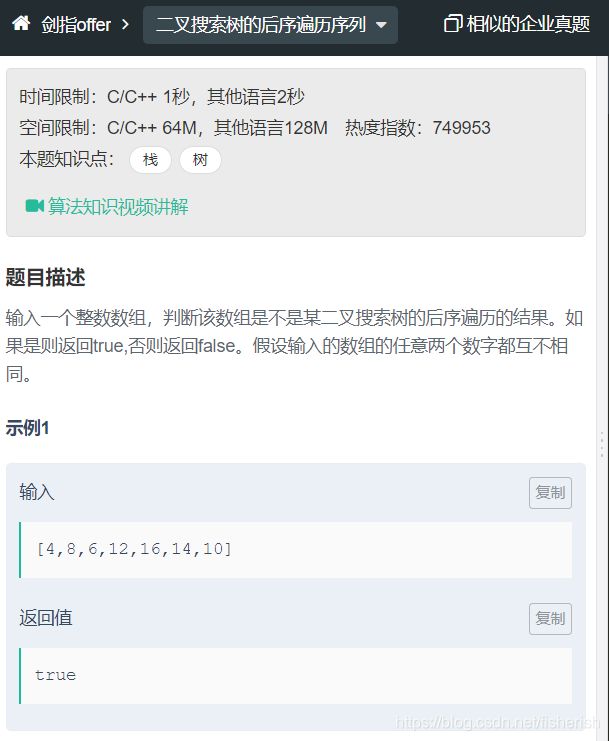
【剑指offer】33. 二叉搜索树的后序遍历序列
// 33. 二叉搜索树的后序遍历序列
// 力扣
// 输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。
// 如果是则返回 true,否则返回 false。假设输入的数组的任意两个数
// 字都互不相同。
// 牛客
// 输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。
// 如果是则返回true,否则返回false。假设输入的数组的任意两个数字都互
// 不相同。
题解
// 首先关键抓手是 后序遍历 和 二叉搜索树(BST)
// 后序遍历的特点是取值会先取根节点的左树,然后取根节点的右树,最后才取根节点
// 而BST特点是左树结点值比根节点值小,根节点值又比右树结点值小,位置越靠左的越小
// 因此根据后序遍历的左右树先后顺序,和左右树大小问题,找到根节点之后就可以找
// 把左树元素和右树元素分离。分离之后继续找左子树右子树根节点,再把左子树右子树
// 各自的左右子树元素分离,以此循环下去。能够分离出来的就满足条件,
// 不能够分离出来的就返回false
// 力扣
// 执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
// 内存消耗:36.1 MB, 在所有 Java 提交中击败了23.01%的用户
class Solution {
public boolean verifyPostorder(int[] postorder) {
if (postorder.length == 0)
return true;
int head = 0;
int end = postorder.length - 1;
return recur(postorder, head, end);
}
private boolean recur(int[] postorder, int head, int end) {
if (head >= end) // 若head大于end或相等,遍历完成,返回true
return true;
int index = head; // 索引index用于从head到end遍历所有元素
// 若是后序遍历,postorder[end]必为根节点
// 根节点的左子树判断,若是BST,左子树元素必小于根节点postorder[end]
while (postorder[index] < postorder[end])
index++;
int mid = index; // 左子树
// 与左子树同理
while (postorder[index] > postorder[end])
index++;
// 若index能到达end(不满足条件时,index走不完postorder)
// 在左子树元素序列中递归recur
// 再右子树元素序列中递归recur
return (index == end) && recur(postorder, head, mid - 1) && recur(postorder, mid, end - 1);
}
}
// 牛客
// 运行时间:10ms
// 占用内存:9648k
public class Solution {
public boolean VerifySquenceOfBST(int [] sequence) {
if (sequence.length == 0)
return false;
int head = 0;
int end = sequence.length - 1;
return recur(sequence, head, end);
}
private boolean recur(int[] sequence, int head, int end) {
if (head >= end)
return true;
int index = head;
while (sequence[index] < sequence[end])
index++;
int mid = index;
while (sequence[index] > sequence[end])
index++;
return (index == end) && recur(sequence, head, mid - 1) && recur(sequence, mid, end - 1);
}
}
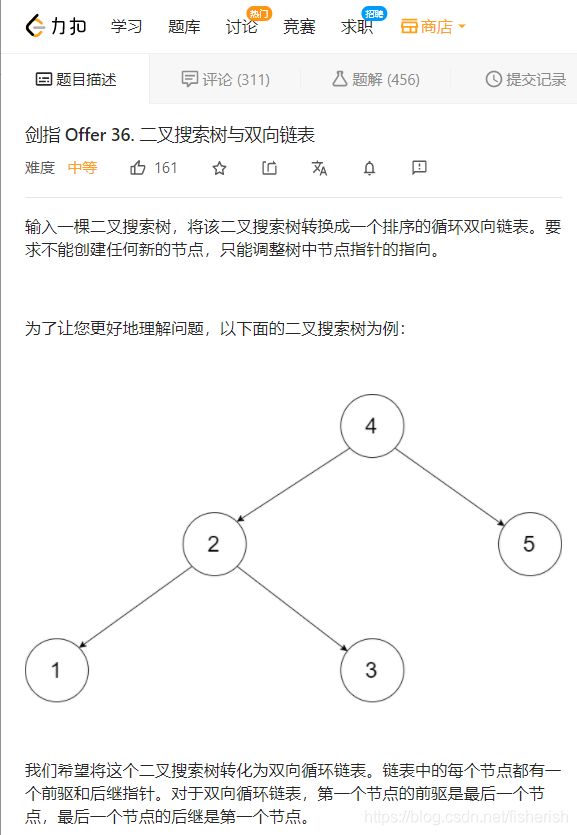
【剑指offer】36. 二叉搜索树与双向链表
题目描述
// 36. 二叉搜索树与双向链表
// 力扣
// 输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表
// 。要求不能创建任何新的节点,只能调整树中节点指针的指向。
// 我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一
// 个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点
// ,最后一个节点的后继是第一个节点。
// 特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左
// 指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一
// 个节点的指针。
// 牛客
// 输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能
// 创建任何新的结点,只能调整树中结点指针的指向。
题解
// 二叉搜索树(BST)的中序遍历可以按照升序取元素,
// 因此通过中序遍历构建双向指针,最后再打通循环即可(力扣)。
// 力扣
// 注意力扣这里需要双向循环链表,所以比牛客要稍微难一丢丢
// 执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
// 内存消耗:37.6 MB, 在所有 Java 提交中击败了89.23%的用户
class Solution {
private Node pre = null;
private Node head = null;
public Node treeToDoublyList(Node root) {
if (root == null)
return null;
// 开始中序遍历,以升序遍历BST结点。
inOrder(root);
// 遍历完,pre在链表尾结点,把头尾结点搭建双向指针
pre.right = head;
head.left = pre;
return head; // 返回链表头指针
}
// 中序遍历函数
private void inOrder(Node node) {
if (node == null)
return;
inOrder(node.left);
// 在两个中序遍历函数之间,即为当前结点遍历位置。
// 如果pre为空,说明node是链表头结点
// 如果pre非空,说明中序遍历已经过了头结点,node遍历到了下一个结点
// 而此时pre还在上一个结点位置(头结点),这就可以在pre和node之间搭建双向指针
if (pre != null) {
node.left = pre; // node上一结点指向pre
pre.right = node; // pre下一结点指向node
}
else // pre为空,说明node是链表头结点,令head指向链表头结点
head = node;
pre = node; // pre移动至node(移动至下一个遍历节点)
inOrder(node.right);
}
}
// 牛客
// 牛客需要稍微修改一下,牛客这里只需要双向链表,没说要双向循环链表
// 运行时间:10ms
// 占用内存:9876k
public class Solution {
private TreeNode pre = null;
private TreeNode head = null;
public TreeNode Convert(TreeNode pRootOfTree) {
if (pRootOfTree == null)
return null;
// 开始中序遍历,以升序遍历BST结点。
inOrder(pRootOfTree);
return head; // 返回链表头指针
}
private void inOrder(TreeNode node) {
if (node == null)
return;
inOrder(node.left);
if (pre != null) {
node.left = pre;
pre.right = node;
}
else
head = node;
pre = node;
inOrder(node.right);
}
}
【剑指offer】54. 二叉搜索树的第k大节点
题目描述
// 54. 二叉搜索树的第k大节点
// 力扣
// 给定一棵二叉搜索树,请找出其中第k大的节点。
// 牛客
// 给定一棵二叉搜索树,请找出其中的第k小的TreeNode结点。
题解
/
// 中序遍历的非递归方法
// 这题建议先做牛客,再做力扣
// 还记得BST的性质:左子结点比根节点小,根节点比右子结点小
// 且BST的中序遍历出来的元素是升序的。
// 牛客
// 牛客题目简单,找第k小的结点,直接中序遍历,中序遍历出来的元素就是
// 升序的,直接返回遍历的第k个结点。
// 我们创建一个count计数位,计数遍历的结点个数,数到第k个,直接返回结点。
// 运行时间:16ms,超过92.82%用Java提交的代码
// 占用内存:9872KB,超过11.21%用Java提交的代码
import java.util.Stack;
public class Solution {
public int count = 0;
TreeNode res;
TreeNode KthNode(TreeNode pRoot, int k) {
if (pRoot == null)
return null;
return inorder(pRoot, k);
}
// 中序遍历的非递归遍历
private TreeNode inorder(TreeNode root, int k) {
Stack stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
cur = stack.pop();
count++;
if (cur != null && count == k) {
res = cur;
return res;
}
cur = cur.right;
}
return null;
}
}
// 力扣
// 力扣的题目稍微难一点,需要找第k大的结点。就需要找到降序遍历结点的方法,
// 其实很简单,也是中序遍历,把中序遍历的 左-根-右,改成 右-根-左 即可。
// 其他部分跟牛客解法一模一样。
// 执行用时:1 ms, 在所有 Java 提交中击败了41.99%的用户
// 内存消耗:38.4 MB, 在所有 Java 提交中击败了41.12%的用户
class Solution {
public int count = 0;
TreeNode res;
public int kthLargest(TreeNode root, int k) {
if (root == null)
return -1;
return inorder(root, k);
}
private int inorder(TreeNode root, int k) {
Stack stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
cur = cur.right;
}
cur = stack.pop();
count++;
if (cur != null && count == k) {
res = cur;
return res.val;
}
cur = cur.left;
}
return -1;
}
}
// 中序遍历的递归方法
// 牛客
// 运行时间:17ms,超过87.35%用Java提交的代码
// 占用内存:9984KB,超过5.38%用Java提交的代码
public class Solution {
public int count = 0;
TreeNode res;
TreeNode KthNode(TreeNode pRoot, int k) {
if (pRoot == null)
return null;
inorder(pRoot, k);
return res;
}
// 中序遍历的非递归遍历
private void inorder(TreeNode root, int k) {
if (root == null)
return;
inorder(root.left, k);
count++;
if (count == k)
res = root;
inorder(root.right, k);
}
}
// 力扣
// 执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
// 内存消耗:38.2 MB, 在所有 Java 提交中击败了75.05%的用户
class Solution {
public int count = 0;
TreeNode res = null;
public int kthLargest(TreeNode root, int k) {
if (root == null)
return -1;
inorder(root, k);
return (res == null) ? -1 : res.val;
}
private void inorder(TreeNode root, int k) {
if (root == null)
return;
inorder(root.right, k);
count++;
if (count == k)
res = root;
inorder(root.left, k);
}
}
【剑指offer】68. 二叉搜索树的最近公共祖先
题目描述
// 68. 二叉搜索树的最近公共祖先
// 力扣
// 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
// 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,
// 最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽
// 可能大(一个节点也可以是它自己的祖先)。”
// 例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
题解
// 力扣
// 二叉搜索树(BST)查找结点的公共祖先
// 二叉搜索树是左子树数值小于根结点,根结点数值小于右子树的二叉树。
//
// 根据p和q的情况可以分成:
// 1.p和q不在同一个子树中,则公共祖先存在于p和q的父结点以上,且公共祖先
// 一定是p和q所在子树分支的根结点。
// 2.p在q的左/右子树中,公共祖先就是q,
// 3.q在p的左/右子树中,公共祖先就是p。
//
// 也就是说,如果p p.val && res.val > q.val)
res = lowestCommonAncestor(res.left, p, q);
if (res.val < p.val && res.val < q.val)
res = lowestCommonAncestor(res.right, p, q);
return res;
}
}
// 简略
// 效率不高
// 执行用时:8 ms, 在所有 Java 提交中击败了12.99%的用户
// 内存消耗:39.1 MB, 在所有 Java 提交中击败了61.45%的用户
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null)
return null;
if (root.val > p.val && root.val > q.val)
return lowestCommonAncestor(root.left, p, q);
if (root.val < p.val && root.val < q.val)
return lowestCommonAncestor(root.right, p, q);
return root;
}
}
特殊解——二叉平衡树(AVL)
【剑指offer】55.2 平衡二叉树
// 55.2 平衡二叉树
// 力扣
// 输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果某二叉
// 树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡
// 二叉树。
// 牛客
// 输入一棵二叉树,判断该二叉树是否是平衡二叉树。在这里,我们只需要
// 考虑其平衡性,不需要考虑其是不是排序二叉树平衡二叉树(Balanced B
// inary Tree),具有以下性质:它是一棵空树或它的左右两个子树的高度
// 差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
题解
/ 遍历检查 /
// 力扣
// 不高效的实现,思路可以借鉴
// 构建一个前序遍历,遍历每个结点,在每个结点处调用55题中的深度函数
// 找深度差,每个结点的左右子树的深度差的绝对值不大于1说明是AVL
// 执行用时:90 ms, 在所有 Java 提交中击败了6.49%的用户
// 内存消耗:39 MB, 在所有 Java 提交中击败了5.57%的用户
class Solution {
public boolean res = true;
public boolean isBalanced(TreeNode root) {
if (root == null)
return res;
preOrder(root);
return res;
}
private void preOrder(TreeNode root) {
if (root == null)
return;
if (Math.abs(searchDepth(root.left) - searchDepth(root.right)) > 1)
res = false;
preOrder(root.left);
preOrder(root.right);
}
private int searchDepth(TreeNode root) {
if (root == null)
return 0;
return 1 + Math.max(searchDepth(root.left), searchDepth(root.right));
}
}
// 牛客
// 运行时间:13ms,超过70.05%用Java提交的代码
// 占用内存:9684KB,超过4.13%用Java提交的代码
public class Solution {
public boolean res = true;
public boolean IsBalanced_Solution(TreeNode root) {
if (root == null)
return res;
preOrder(root);
return res;
}
private void preOrder(TreeNode root) {
if (root == null)
return;
if (Math.abs(searchDepth(root.left) - searchDepth(root.right)) > 1)
res = false;
preOrder(root.left);
preOrder(root.right);
}
private int searchDepth(TreeNode root) {
if (root == null)
return 0;
return 1 + Math.max(searchDepth(root.left), searchDepth(root.right));
}
}
/ 高效实现 //
// 力扣
// 高效实现,如果每个结点的左右子树的深度差的绝对值不大于1,则继续递归
// ,如果所有的判断函数isBalanced都是true,最终就会返回true,否则如果if
// 满足不了,就会返回false.
// 执行用时:1 ms, 在所有 Java 提交中击败了100.00%的用户
// 内存消耗:38.8 MB, 在所有 Java 提交中击败了11.86%的用户
class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null)
return true;
if (Math.abs(searchDepth(root.left) - searchDepth(root.right)) <= 1) {
return isBalanced(root.left) && isBalanced(root.right);
}
else
return false;
}
private int searchDepth(TreeNode root) {
if (root == null)
return 0;
return 1 + Math.max(searchDepth(root.left), searchDepth(root.right));
}
}
// 牛客
// 运行时间:11ms,超过83.09%用Java提交的代码
// 占用内存:9680KB,超过4.28%用Java提交的代码
public class Solution {
public boolean IsBalanced_Solution(TreeNode root) {
if (root == null)
return true;
if (Math.abs(searchDepth(root.left) - searchDepth(root.right)) <= 1) {
return IsBalanced_Solution(root.left) && IsBalanced_Solution(root.right);
}
else
return false;
}
private int searchDepth(TreeNode root) {
if (root == null)
return 0;
return 1 + Math.max(searchDepth(root.left), searchDepth(root.right));
}
}