【剑指offer】数据结构——队列 栈 堆
目录
- 数据结构——树
-
- 【剑指offer】09.用两个栈实现队列
- 【剑指offer】30. 包含min函数的栈
- 【剑指offer】31. 栈的压入、弹出序列
- 【剑指offer】41. 数据流中的中位数
- 【剑指offer】59.2 队列的最大值
数据结构——树
【剑指offer】09.用两个栈实现队列
题目描述
牛客:
用两个栈来实现一个队列,完成队列的Push和Pop操作。 队列中的元素为int类型。
leetcode
用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 )
题解
// 牛客
// 用两个栈来实现一个队列,完成队列的Push和Pop操作。 队列中的元素为int类型。
import java.util.Stack;
public class Solution {
Stack stack1 = new Stack();
Stack stack2 = new Stack();
public void push(int node) {
stack1.push(node);
}
public int pop() {
if (stack2.isEmpty())
while (!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
return stack2.pop();
}
}
// 力扣
// 09. 用两个栈实现队列
// 用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail
// 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整
// 数的功能。(若队列中没有元素,deleteHead 操作返回 -1 )
// 63 ms , 在所有 Java 提交中击败了 31.32% 的用户
// 46.6 MB , 在所有 Java 提交中击败了 70.90% 的用户
import java.util.Stack;
class CQueue {
// 定义栈变量
private Stack stack1;
private Stack stack2;
public CQueue() {
stack1 = new Stack<>(); // 赋予对象
stack2 = new Stack<>();
}
public void appendTail(int value) {
stack1.push(value);
}
public int deleteHead() {
// 如果stack2是非空,则不往里存元素,直接看要不要弹出
//如果stack2空,从stack1中出栈往里存
if (stack2.isEmpty()) {
while (!stack1.isEmpty()) { // 直到把stack1掏空为止
stack2.push(stack1.pop());
}
}
// 如果stack2空,且stack1也空,有可能导致转移完元素的stack2
// 依然是空的,此时stack2.pop()会报错,所以还要检查一下非空
if (!stack2.isEmpty())
return stack2.pop()
return -1; // 如果真的没元素可取,直接返回-1
}
}
【剑指offer】30. 包含min函数的栈
题目描述
// 力扣
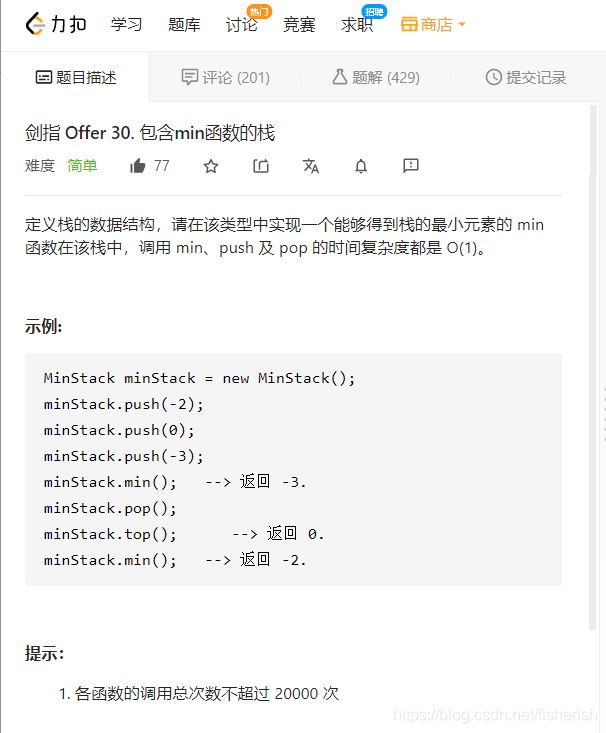
// 定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的
// min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。
// 牛客
// 定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的
// min函数(时间复杂度应为O(1))。
题解
// 这题要求O(1)复杂度,遍历数据结构的所有位置找最小值肯定是不可能的,
// 这就需要新创建一个栈minstack用于专门存储push进栈A的最小的值,
// 并且把最小值一直置于minstack的栈顶,这样需要的时候直接弹出就是O(1)
// 复杂度了。
// 总的来说,minstack只用于存储最小或曾经的最小值,如果minstack
// 为空,push时直接压进去,如果minstack非空,则push之前先判断压入元素
// 与minstack栈顶元素谁比较小,取小的那个数压入。
// (如果压入元素不比minstack栈顶元素小也没关系,这样会重新压一个
// minstack栈顶元素进去,保证了minstack和dataStack两个栈的长度一致)
// 牛客
// 运行时间:11ms
// 占用内存:9796k
import java.util.Stack;
public class Solution {
private Stack minStack = new Stack<>();
private Stack dataStack = new Stack<>();
public void push(int node) {
if (minStack.isEmpty())
minStack.push(node);
else // 取minStack栈顶元素和压入元素最小的那个压入
minStack.push(Math.min(minStack.peek(), node));
dataStack.push(node);
}
public void pop() {
dataStack.pop();
minStack.pop();
}
public int top() {
return dataStack.peek();
}
public int min() {
return minStack.peek();
}
}
// 力扣
// 执行用时:21 ms, 在所有 Java 提交中击败了85.37%的用户
// 内存消耗:40.3 MB, 在所有 Java 提交中击败了61.41%的用户
import java.util.Stack;
class MinStack {
private Stack minStack;
private Stack dataStack;
/** initialize your data structure here. */
public MinStack() {
minStack = new Stack<>();
dataStack = new Stack<>();
}
public void push(int x) {
if (minStack.isEmpty())
minStack.push(x);
else {
minStack.push(Math.min(minStack.peek(), x));
}
dataStack.push(x);
}
public void pop() {
dataStack.pop();
minStack.pop();
}
public int top() {
return dataStack.peek();
}
public int min() {
return minStack.peek();
}
}
/**
* Your MinStack object will be instantiated and called as such:
* MinStack obj = new MinStack();
* obj.push(x);
* obj.pop();
* int param_3 = obj.top();
* int param_4 = obj.min();
*/
// 或者可以这样写
// 执行用时:22 ms, 在所有 Java 提交中击败了74.78%的用户
// 内存消耗:40.5 MB, 在所有 Java 提交中击败了13.02%的用户
class MinStack {
private Stack stack;
private Stack minLog;
/** initialize your data structure here. */
public MinStack() {
this.stack = new Stack();
this.minLog = new Stack();
}
public void push(int x) {
stack.push(x);
if (minLog.isEmpty() || minLog.peek() > x) {
minLog.push(x);
}
else {
minLog.push(minLog.peek());
}
}
public void pop() {
stack.pop();
minLog.pop();
}
public int top() {
return stack.peek();
}
public int min() {
return minLog.peek();
}
}
【剑指offer】31. 栈的压入、弹出序列
// 31. 栈的压入、弹出序列
// 力扣
// 输入两个整数序列,第一个序列表示栈的压入顺序,请判断第
// 二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不
// 相等。例如,序列 {1,2,3,4,5} 是某栈的压栈序列,序列 {4
// ,5,3,2,1} 是该压栈序列对应的一个弹出序列,但 {4,3,5,1,2
// } 就不可能是该压栈序列的弹出序列。
// 牛客
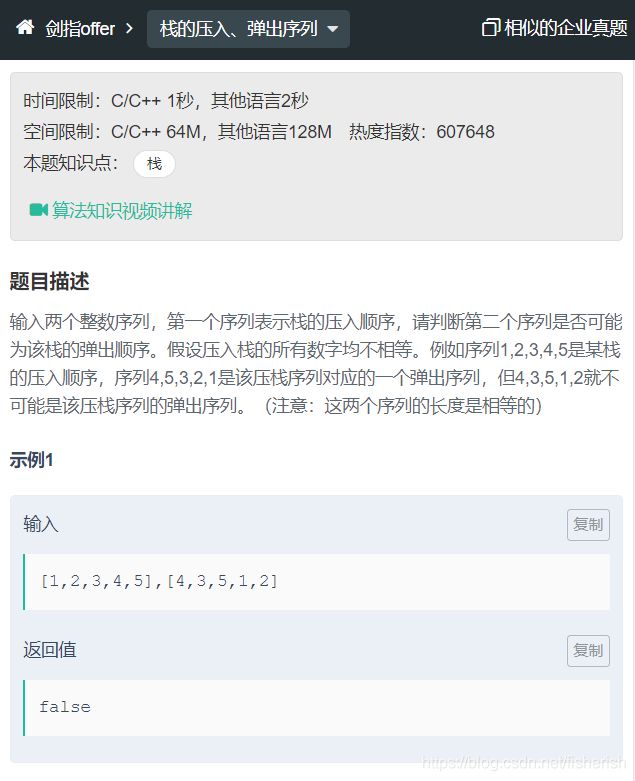
// 输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个
// 序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等
// 。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈
// 序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹
// 出序列。(注意:这两个序列的长度是相等的)
题解
// 题目还是有一定难度的
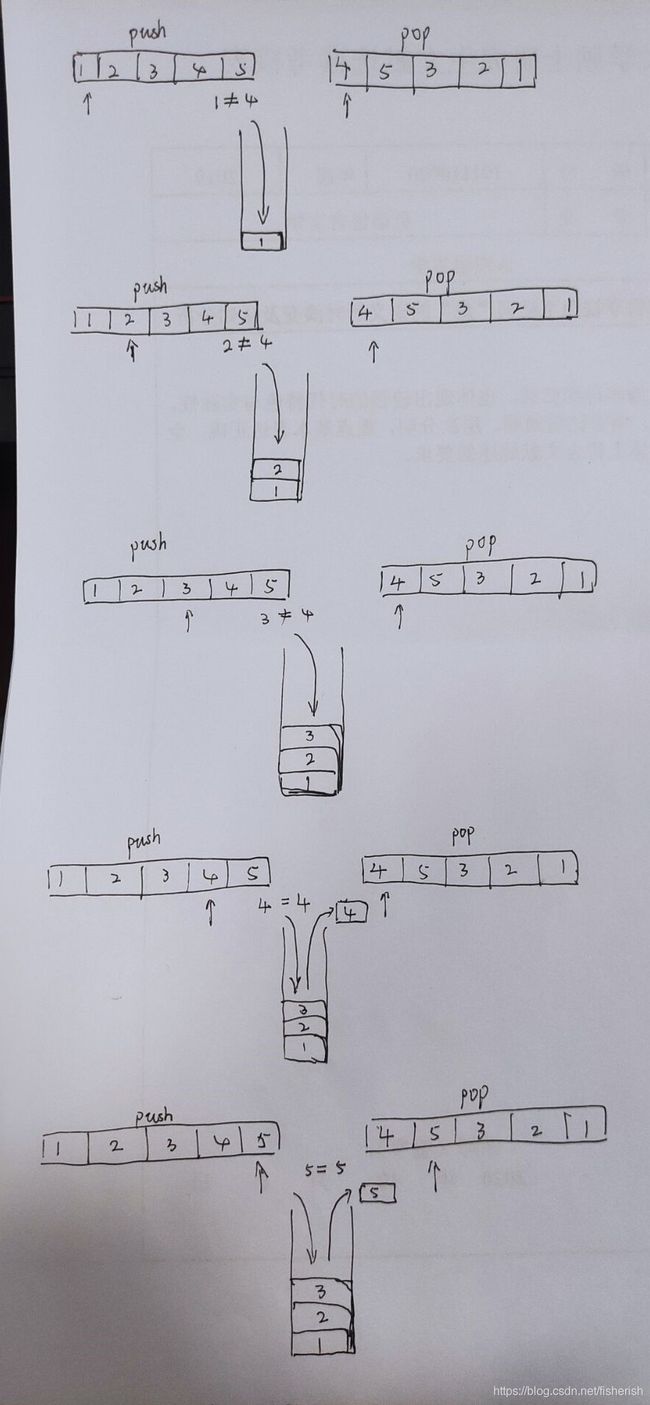
// 需要直接按照题目意思模拟:
// 双指针pop序列和push序列一起遍历,push在前,如果push的元素正好等
// 于pop的元素,则push之后直接pop,如果不相等,压入栈,push指针右移,
// 继续判断。push序列遍历完不能停止,pop序列还要继续遍历,直到栈存储
// 的元素全部弹出,栈中存在弹不出的元素,就返回false了。全部弹出则返
// 回true。
// 力扣
// 比较好理解
// 执行用时:2 ms, 在所有 Java 提交中击败了94.50%的用户
// 内存消耗:38 MB, 在所有 Java 提交中击败了81.85%的用户
import java.util.Stack;
class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
if (pushed.length == 0 && popped.length == 0)
return true;
if (pushed.length == 0 || popped.length == 0) // 排除特殊情况
return false;
int i = 0, j = 0; // 索引 for push and pop
Stack sim = new Stack<>();
// 直到popped指针走完再停止while(弹出操作执行完再停止while)
while (j < popped.length) {
// System.out.println(sim.toString());
// 如果栈顶元素等于弹出序列popped的遍历元素
if (!sim.isEmpty() && sim.peek() == popped[j]) {
sim.pop(); // 弹出
j++; // 指针右移
}
else if (i < pushed.length && pushed[i] == popped[j]) {
sim.push(pushed[i++]); // push遍历元素和pop遍历元素相等
sim.pop(); // 压入再弹出,两个指针右移
j++;
}
else if (i < pushed.length) { // 如果没有可弹出元素,
sim.push(pushed[i++]); // 压入元素,指针右移
}
else // 如果元素全部压入栈了,又没有可弹出元素,直接false
return false;
}
return sim.isEmpty();
}
}
// 力扣
// 稍微精简
import java.util.Stack;
class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
int i = 0, j = 0; // for push and pop
Stack sim = new Stack<>();
while (j < popped.length) {
// System.out.println(sim.toString());
if (!sim.isEmpty() && sim.peek() == popped[j]) {
sim.pop();
j++;
}
else if (i < pushed.length && pushed[i] == popped[j]) {
i++;
j++;
}
else if (i < pushed.length) {
sim.push(pushed[i++]);
}
else
return false;
}
return sim.isEmpty();
}
}
// 力扣
// 逻辑合并一下
// 执行用时:2 ms, 在所有 Java 提交中击败了94.50%的用户
// 内存消耗:38.3 MB, 在所有 Java 提交中击败了36.81%的用户
import java.util.Stack;
class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
int i = 0, j = 0; // for push and pop
Stack sim = new Stack<>();
while (i < pushed.length) {
// System.out.println(sim.toString());
sim.push(pushed[i++]);
while (j < popped.length && !sim.isEmpty() && sim.peek() == popped[j]) {
sim.pop();
j++;
}
}
return sim.isEmpty();
}
}
// 漂亮版
class Solution {
int pop = 0;
int push = 0;
private Stack stack;
public boolean validateStackSequences(int[] pushed, int[] popped) {
this.stack = new Stack();
while (push < pushed.length && pop < popped.length) {
stack.push(pushed[push++]);
while (!stack.isEmpty() && stack.peek() == popped[pop]) {
stack.pop();
pop++;
}
}
return stack.isEmpty();
}
}
// 牛客
// 运行时间:11ms
// 占用内存:9668k
import java.util.Stack;
public class Solution {
public boolean IsPopOrder(int[] pushA, int[] popA) {
int i = 0, j = 0;
Stack sim = new Stack<>();
while (i < pushA.length) {
sim.push(pushA[i++]);
while (j < popA.length && !sim.isEmpty() && sim.peek() == popA[j]) {
sim.pop();
j++;
}
}
return sim.isEmpty();
}
}
【剑指offer】41. 数据流中的中位数
题目描述
// 41. 数据流中的中位数
// 力扣
// 如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,
// 那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中
// 读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平
// 均值。
// 例如,
// [2,3,4] 的中位数是 3
// [2,3] 的中位数是 (2 + 3) / 2 = 2.5
// 设计一个支持以下两种操作的数据结构:
// void addNum(int num) - 从数据流中添加一个整数到数据结构中。
// double findMedian() - 返回目前所有元素的中位数。
// 牛客
// 如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么
// 中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数
// 个数值,那么中位数就是所有数值排序之后中间两个数的平均值。我们使
// 用Insert()方法读取数据流,使用GetMedian()方法获取当前读取数据的中
// 位数。
题解
/ 双堆维护 /
// 数据流要么有奇数个,要么有偶数个。
// 如果监控存入的元素个数size,必然size的变化有:奇数->偶数->奇数->偶数...
// 我们将第奇数个和第偶数个流入的数据分开,并使用最大堆最小堆来保存。
// 这是由于最大堆可以自动维护较小值(通过弹出最大值),最小堆可以自动维护较大值(通过弹出最小值。
// 由于第奇数个数先于第偶数个数存入,所以第奇数个数存入堆A(最大堆
// 还是最小堆无所谓),那么第偶数个数就必须存入堆B(是什么堆无所谓,反正跟A不同就行)
// 这个解里我令第1个,第3个...,这些第奇数个流入的数组存入最小堆,
// 令第2个,第4个...,第偶数个流入的数字存入最大堆。
// 数据在入堆之前还必须经过相反堆的筛选,比如第1个存入的数字规定存入最小堆
// 那么先进入最大堆进行筛选,此时最大堆弹出堆顶值(最大值),再存入最小堆,
// 第2个存入的数字同理,以此类推。
// 则最大堆会遍历数据流里排名奇数位的数字,并弹出的所有大值给最小堆
// 最小堆也会遍历数据流也排名偶数位的数字,并弹出所有的小值给最大堆。
// 经过这样的筛选,所有的大值都会给最小堆,所有的小值都会给最大堆。
// 求中位数时,只需看堆顶元素和数据流个数即可。
// 如果数据总数有偶数个,那么取大值里的最小值(最小堆堆顶)和
// 小值里的最大值(最大堆堆顶)求和÷2即可得到中位数。
// 如果数据总数为奇数个,取第奇数个存入堆(是最大堆还是最小堆无所谓)
// 的堆顶元素,就是中位数。
// 牛客
// 此解设第奇数个数字的存储堆为最小堆,第偶数个数据的存储堆为最大堆
// 运行时间:16ms
// 占用内存:10044k
import java.util.PriorityQueue;
import java.util.Comparator;
public class Solution {
// 最大堆maxHeap:用于筛选大值传入最小堆minHeap,自身用于保存小值。
private PriorityQueue maxHeap = new PriorityQueue<>( new Comparator() {
@Override
public int compare(Integer o1, Integer o2) {
return o2.compareTo(o1);
}
});
// 最小堆minHeap:用于筛选小值传入最大堆maxHeap,自身用于保存大值。
private PriorityQueue minHeap = new PriorityQueue<>();
private int size = 0; // size让我们监控所有元素的总数
public void Insert(Integer num) {
// 如果已有偶数个元素,则将第奇数个元素num,存入最大堆中
// ,筛选出最大堆的最大值弹出,存入最小堆中。
// 如果当前数num在最大堆maxHeap就是最大值,会被直接存入
// 最小堆minHeap,如果在maxHeap中不是最大值,那么会maxHeap
// 会自己推出一个堆内当前的最大值给minHeap,相当于做了数据交换。
if (size % 2 == 0) {
maxHeap.add(num);
minHeap.add(maxHeap.poll());
}
else { // 如果已有奇数个元素,则将第偶数个元素存入最小堆中
minHeap.add(num);
// 后将最小堆中最小值弹出(筛选),存入最大堆中。
maxHeap.add(minHeap.poll());
}
size++; // 每存入一个数据,size+1,记录元素的总数
}
public Double GetMedian() {
// 两个堆元素相同,元素个数为偶数
if (maxHeap.size() == minHeap.size())
return (double) (maxHeap.peek() + minHeap.peek()) / 2.0;
else
return (double) minHeap.peek();
}
}
// 牛客
// 此解设第奇数个数字的存储堆为最大堆,第偶数个数据的存储堆为最小堆
// 运行时间 18ms
// 占用内存 10180KB
import java.util.PriorityQueue;
import java.util.Comparator;
public class Solution {
private PriorityQueue maxHeap = new PriorityQueue<>( new Comparator() {
@Override
public int compare(Integer o1, Integer o2) {
return o2.compareTo(o1);
}
});
private PriorityQueue minHeap = new PriorityQueue<>();
private int size = 0;
public void Insert(Integer num) {
if (size % 2 == 0) {
minHeap.add(num);
maxHeap.add(minHeap.poll());
}
else {
maxHeap.add(num);
minHeap.add(maxHeap.poll());
}
size++;
}
public Double GetMedian() {
if (maxHeap.size() == minHeap.size())
return (double) (maxHeap.peek() + minHeap.peek()) / 2.0;
else
return (double) maxHeap.peek();
}
}
// 力扣
// 此解设第奇数个数字的存储堆为最小堆,第偶数个数据的存储堆为最大堆
// 执行用时:88 ms, 在所有 Java 提交中击败了34.84%的用户
// 内存消耗:49.4 MB, 在所有 Java 提交中击败了84.64%的用户
import java.util.PriorityQueue;
import java.util.Comparator;
class MedianFinder {
private PriorityQueue maxHeap, minHeap;
int size;
public MedianFinder() {
maxHeap = new PriorityQueue<>(new Comparator() {
@Override
public int compare(Integer o1, Integer o2) {
return o2.compareTo(o1);
}
});
minHeap = new PriorityQueue<>();
size = 0;
}
public void addNum(int num) {
if (size % 2 == 0) {
maxHeap.add(num);
minHeap.add(maxHeap.poll());
}
else {
minHeap.add(num);
maxHeap.add(minHeap.poll());
}
size++;
}
public double findMedian() {
if (minHeap.size() == maxHeap.size())
return (double) (minHeap.peek() + maxHeap.peek()) / 2.0;
else
return (double) minHeap.peek();
}
}
/**
* Your MedianFinder object will be instantiated and called as such:
* MedianFinder obj = new MedianFinder();
* obj.addNum(num);
* double param_2 = obj.findMedian();
*/
// 力扣
// 此解设第奇数个数字的存储堆为最大堆,第偶数个数据的存储堆为最小堆
// 执行用时:92 ms, 在所有 Java 提交中击败了26.29%的用户
// 内存消耗:49.7 MB, 在所有 Java 提交中击败了43.06%的用户
import java.util.PriorityQueue;
import java.util.Comparator;
class MedianFinder {
private PriorityQueue maxHeap, minHeap;
int size;
public MedianFinder() {
maxHeap = new PriorityQueue<>(new Comparator() {
@Override
public int compare(Integer o1, Integer o2) {
return o2.compareTo(o1);
}
});
minHeap = new PriorityQueue<>();
size = 0;
}
public void addNum(int num) {
if (size % 2 == 0) {
minHeap.add(num);
maxHeap.add(minHeap.poll());
}
else {
maxHeap.add(num);
minHeap.add(maxHeap.poll());
}
size++;
}
public double findMedian() {
if (minHeap.size() == maxHeap.size())
return (double) (minHeap.peek() + maxHeap.peek()) / 2.0;
else
return (double) maxHeap.peek();
}
}
【剑指offer】59.2 队列的最大值
// 59.2 队列的最大值
// 力扣
// 请定义一个队列并实现函数 max_value 得到队列里的最大值,要求函数m
// ax_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。
// 若队列为空,pop_front 和 max_value 需要返回 -1
题解
// 力扣
// 数组辅助法
// 执行用时:70 ms, 在所有 Java 提交中击败了6.10%的用户
// 内存消耗:46.3 MB, 在所有 Java 提交中击败了63.28%的用户
class MaxQueue {
List list;
Queue queue;
public MaxQueue() {
list = new ArrayList();
queue = new LinkedList();
}
public int max_value() {
if (queue.isEmpty())
return -1;
Collections.sort(list);
return list.get(list.size() - 1);
}
// 从背后(back)入队
public void push_back(int value) {
queue.add(value);
list.add(value);
}
// 从前面(front)出队
public int pop_front() {
if (queue.isEmpty())
return -1;
int out = queue.remove();
list.remove(list.indexOf(out));
return out;
}
}
/**
* Your MaxQueue object will be instantiated and called as such:
* MaxQueue obj = new MaxQueue();
* int param_1 = obj.max_value();
* obj.push_back(value);
* int param_3 = obj.pop_front();
*/
// 力扣
// 双端队列辅助法
// 执行用时:41 ms, 在所有 Java 提交中击败了55.00%的用户
// 内存消耗:46.4 MB, 在所有 Java 提交中击败了47.06%的用户
class MaxQueue {
Deque deque;
Queue queue;
public MaxQueue() {
deque = new LinkedList();
queue = new LinkedList();
}
public int max_value() {
if (queue.isEmpty())
return -1;
return deque.peekFirst();
}
// 从背后(back)入队
public void push_back(int value) {
while (!deque.isEmpty() && deque.peekLast() < value) {
deque.pollLast();
}
deque.offerLast(value);
queue.offer(value);
}
// 从前面(front)出队
public int pop_front() {
if (queue.isEmpty())
return -1;
int res = queue.poll();
if (res == deque.peekFirst()) {
deque.pollFirst();
}
return res;
}
}