leetcode二分查找算法总结

875猴子吃香蕉

1011货物运输

 

 

正常版本

/**
 * 二分查找，找到该值在数组中的下标，否则为-1
 */
public static int binarySerach(int[] array, int key) {
    int left = 0;
    int right = array.length - 1;
 
    // 这里必须是 <=
    while (left <= right) {
        int mid = left + (right-left)/2;  // 养成习惯
        if (array[mid] == key) {
            return mid;
        }
        else if (array[mid] < key) {
            left = mid + 1;
        }
        else {
            right = mid - 1;
        }
    }
 
    return -1;
}
加强版1：查找第一个与key相等的元素
查找第一个相等的元素，也就是说等于==查找key值的元素有好多个==，返回这些元素==最左边==的元素下标。

// 查找第一个相等的元素
public static int findFirstEqual(int[] array, int key) {
    int left = 0;
    int right = array.length - 1;
 
    // 这里必须是 <=
    while (left <= right) {
        int mid = left + (right-left)/2;
        if (array[mid] >= key) {   // ==更改的地方== 即发现第一个=的时候
            right = mid - 1;
        }
        else {
            left = mid + 1;
        }
    }
    if (left < array.length && array[left] == key) {
        return left;
    }
    
    return -1;
}
加强版2：查找最后一个与key相等的元素
查找最后一个相等的元素，也就是说等于查找key值的==元素有好多个==，返回这些元素==最右边==的元素下标。

// 查找最后一个相等的元素
static int findLastEqual(int[] array, int key) {
    int left = 0;
    int right = array.length - 1;
 
    // 这里必须是 <=
    while (left <= right) {
        int mid = left + (right-left)/2;
        if (array[mid] <= key) {  // ===更改的地方===
            left = mid + 1;
        }
        else {
            right = mid - 1;
        }
    }
    if (right >= 0 && array[right] == key) {
        return right;
    }
 
    return -1;
}
总结： 套路+思考
// 这里必须是 <=
while (left <= right) {
    int mid = left + (right-left)/2;
    if (array[mid] ? key) {    /// 比较符号
        //... right = mid - 1;
    }
    else {
        // ... left = mid + 1;
    }
}
return xxx;                 // 返回值
1 首先判断出是返回left，还是返回right

最后的跳出条件是 left > right ，left和right 是key的边界地方，看需求，选择其中一个

2 判断出比较符号

看 中间值 与 key的 关系 。
————————————————

 

二分查找(binary search)是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。二分查找算法在情况下的复杂度是对数时间，进行次比较操作。

二分查找有很多等价写法，判断搜索循环条件，左右边界更新方式的选择需要配合，否则容易出现死循环或者遗漏区域。在这里给出两个框架，根据具体问题选择适当的框架解决。

常见的二分查找通常在左闭右闭区间[left,right]范围内进行搜索，循环条件为，左边界更新为left = mid + 1，右边界更新为right = mid - 1。

class Solution:
    def searchIndex(self, nums: List[int], target: int) -> int:
        left = 0
        right = len(nums) - 1
        while left <= right:
            mid = left + (right - left) // 2    # 防止(left+right)太大而溢出
            if nums[mid] == target:
                return mid
            elif nums[mid] < target:
                left = mid + 1
            else:
                right = mid - 1
        return -1
上面的做法当mid没有找到恰好满足条件的解，需要对左右边界进行判断时，左右边界不等，使判断变得复杂。而使用左闭右开区间[left,right)时，使用下述算法框架可保证left==right，只需判断一个位置即可。

class Solution:
    def searchIndex(self, nums: List[int], target: int) -> int:
        left = 0
        right = len(nums)
        while left < right:
            mid = left + (right - left) // 2    # 防止(left+right)太大而溢出
            if nums[mid] == target:
                return mid
            elif nums[mid] < target:
                left = mid + 1
            else:
                right = mid
        return -1
35.搜索插入位置
给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

你可以假设数组中无重复元素。

输入: [1,3,5,6], 5
输出: 2

输入: [1,3,5,6], 2
输出: 1

class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        left = 0
        right = len(nums)
        while left < right:
            mid = left + (right - left) // 2
            if nums[mid] == target:
                return mid
            elif nums[mid] < target:
                left = mid + 1
            else:
                right = mid
        return left
69.x的平方根
实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

输入: 4
输出: 2

输入: 8
输出: 2
说明: 8 的平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

x的平方根不会超过x的一半，所以将右边界设置为x / 2 + 1

class Solution:
    def mySqrt(self, x: int) -> int:
        if x==0 or x==1:
            return x
        left = 1
        right = x // 2 + 1
        while left < right:
            mid = left + (right - left) // 2
            if mid * mid == x:
                return mid
            elif mid * mid < x:
                left = mid + 1
            else:
                right = mid
        return left - 1
34.在排序数组中查找元素的第一个和最后一个位置
给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

你的算法时间复杂度必须是 O(log n) 级别。

如果数组中不存在目标值，返回 [-1, -1]。

输入: nums = [5,7,7,8,8,10], target = 8
输出: [3,4]

输入: nums = [5,7,7,8,8,10], target = 6
输出: [-1,-1]

一开始的想法使用二分查找找出目标值所在的任意一个索引，再向前后分别遍历。但这种算法在最坏情况下时间复杂度为O(n)，即整个数组内值全为target。因此使用两个二分查找，分别查找目标值的左边界和右边界。

class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
        ret = [-1,-1]
        ret[0] = self.searchLeft(nums,target)
        ret[1] = self.searchRight(nums,target)
        return ret
 
 
    def searchLeft(self,nums,target):
        left = 0
        right = len(nums) - 1
        while left <= right:
            mid = left + (right - left) // 2
            if nums[mid] == target:
                if mid == 0 or nums[mid-1] != target:
                    return mid
                else:
                    right = mid - 1  # 不是左边界，继续二分查找
            elif target > nums[mid]:
                left = mid + 1
            else:
                right = mid - 1 
        return -1
 
    def searchRight(self,nums,target):
        left = 0
        right = len(nums) - 1
        while left <= right:
            mid = left + (right - left) // 2
            if nums[mid] == target:
                if mid == len(nums) - 1 or nums[mid+1] != target:
                    return mid
                else:
                    left = mid + 1  # 不是右边界，继续二分查找
            elif target > nums[mid]:
                left = mid + 1
            else:
                right = mid - 1
        return -1
153.寻找旋转排序数组中的最小值
假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

请找出其中最小的元素。

你可以假设数组中不存在重复元素。

输入: [3,4,5,1,2]
输出: 1

输入: [4,5,6,7,0,1,2]
输出: 0

如果mid处值小于前一个值，则mid处值为解返回，若mid==0，则判断其与nums[1]值的大小关系。判断区间内数组是否为有序数组，若有序，返回区间的第一个值nums[left]，若仍为旋转数组，通过mid处的值与left，right处值比较，判断继续在左区间搜索or右区间搜索。

class Solution:
    def findMin(self, nums: List[int]) -> int:
        if len(nums)==1:
            return nums[0]
        left = 0
        right = len(nums) - 1
        while left <= right:
            mid = left + (right - left) // 2
            if mid == 0 and nums[1] < nums[0]:
                return nums[1]
            elif mid != 0 and nums[mid-1] > nums[mid]:
                return nums[mid]
            else:
                if nums[left] > nums[right]:
                    if nums[mid] > nums[right]:
                        left = mid + 1
                    else:
                        right = mid - 1
                else:
                    return nums[left]
33.搜索旋转排序数组
假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。

你可以假设数组中不存在重复的元素。

你的算法时间复杂度必须是 O(log n) 级别。

输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4

输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1

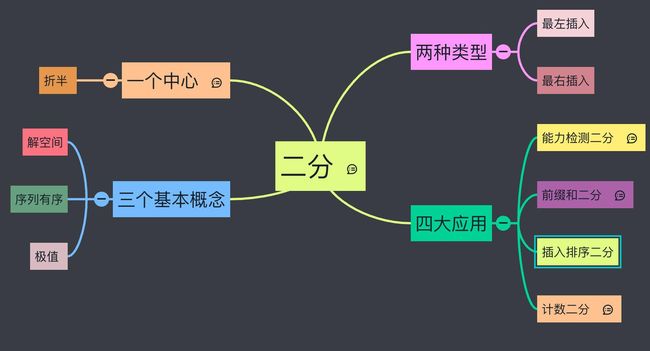
此题为部分有序的数组，且要求复杂度为O(log n)，暗示需使用二分搜索算法。由于数组部分有序，需尤其注意如何更新左右边界。有序数组当target>nums[mid]时，应继续搜索右半部分，即更新左边界。但有一种情况需要在左半部分进行搜索，把当前的数组看作两个有序数组的拼接，当mid落在第二个有序数组内，且target比第二个有序数组的最大值还大，此时要查找的值在第一个有序数组内，此时，更新右边界。当target

注：当然也可先使用上一题的方式找到旋转位置，再在两个有序的数组内进行二分查找

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left = 0
        right = len(nums) - 1
        while left <= right:
            mid = left + (right - left) // 2
            if nums[mid] == target:
                return mid
            elif target > nums[mid]:
                # 在左边搜索，需要满足两个条件
                if nums[mid] < nums[left] and nums[right] < target: 
                    right = mid - 1
                else:
                    left = mid + 1
            else:
                # 在右边搜索，需要满足两个条件
                if nums[mid] > nums[right] and target < nums[left]: 
                    left = mid + 1
                else:
                    right = mid - 1
        return -1
81.搜索旋转排序数组2
假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,0,1,2,2,5,6] 可能变为 [2,5,6,0,0,1,2] )。

编写一个函数来判断给定的目标值是否存在于数组中。若存在返回 true，否则返回 false。

这是搜索旋转排序数组的延伸题目，本题中的nums可能包含重复元素。

输入: nums = [2,5,6,0,0,1,2], target = 0
输出: true

输入: nums = [2,5,6,0,0,1,2], target = 3
输出: false

继续按照上题的思路解决本题，由于有重复数字，使得target在第一个有序数组还是第二个的边界判断更加复杂。在边界处跳过所有重复数字，然后进行判断。最坏情况下有很多重复数字，遍历数组，时间复杂度为O(n)

class Solution:
    def search(self, nums: List[int], target: int) -> bool:
        left = 0
        right = len(nums) - 1
        while left <= right:
            mid = left + (right - left) // 2
            if nums[mid] == target:
                return True
            elif target > nums[mid]:
                while nums[mid] == nums[left] and mid > left: # 不超过mid
                    left += 1
                if nums[mid] < nums[left] and target >= nums[left]: # 在左边搜索
                    right = mid - 1
                else:
                    left = mid + 1
            else:
                while nums[mid] == nums[right] and mid < right:
                    right -= 1
                if nums[mid] > nums[right] and target <= nums[right]: # 在右边搜索
                    left = mid + 1
                else:
                    right = mid - 1
        return False
74.搜索二维矩阵
编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

输入:
matrix = [
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
target = 3
输出: true
matrix = [
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
target = 13
输出: false

两个二分搜索，先找出target可能在的list，再在这个list中查找是否存在target。

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        if len(matrix) == 0 or len(matrix[0]) == 0: 
            return False
        left = 0
        right = len(matrix)
        while left < right:
            mid = left + (right - left) // 2
            if matrix[mid][0] == target:
                return True
            elif target < matrix[mid][0]:
                right = mid
            else:
                left = mid + 1
        nums = matrix[left-1]
        left = 0
        right = len(nums)
        while left < right:
            mid = left + (right - left) // 2
            if nums[mid] == target:
                return True
            elif target < nums[mid]:
                right = mid
            else:
                left = mid + 1
        return False
162.寻找峰值
峰值元素是指其值大于左右相邻值的元素。

给定一个输入数组 nums，其中 nums[i] ≠ nums[i+1]，找到峰值元素并返回其索引。

数组可能包含多个峰值，在这种情况下，返回任何一个峰值所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞。

输入: nums = [1,2,3,1]
输出: 2
解释: 3 是峰值元素，你的函数应该返回其索引 2。

输入: nums = [1,2,1,3,5,6,4]
输出: 1 或 5 
解释: 你的函数可以返回索引 1，其峰值元素为 2；或者返回索引 5， 其峰值元素为 6。
说明:你的解法应该是 O(logN) 时间复杂度的。

解法比较简单，主要是需要想到只要数组中存在一个元素比相邻元素大，那么沿着它一定可以找到一个峰值（想象山峰的形状）。比较mid与mid+1处值，如果mid较大，则左侧存在峰值，如果 mid + 1 较大，则右侧存在峰值。

class Solution:
    def findPeakElement(self, nums: List[int]) -> int:
        left = 0
        right = len(nums) - 1
        while left < right:
            mid = left + (right - left) // 2
            if nums[mid] < nums[mid+1]:
                left = mid + 1
            else:
                right = mid
        return left
410.分割数组的最大值
给定一个非负整数数组和一个整数 m，你需要将这个数组分成 m 个非空的连续子数组。设计一个算法使得这 m 个子数组各自和的最大值最小。

注意:
数组长度 n 满足以下条件:

1 ≤ n ≤ 1000
1 ≤ m ≤ min(50, n)

输入:
nums = [7,2,5,10,8]
m = 2

输出:
18

解释:
一共有四种方法将nums分割为2个子数组。
其中最好的方式是将其分为[7,2,5] 和 [10,8]，
因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。

在max(nums)和sum(nums)之间进行二分查找，子数组和的范围在这二者之间。对于一个mid，计算根据这个mid能将数组分为几个子数组。如小于m，则还可以继续分组，mid大了，在左侧继续搜索。若大于m证明分组多了，mid小了，在右侧继续搜索。最后返回交点。

class Solution {
    public int splitArray(int[] nums, int m) {
        // 在 max(nums) 和 sum(nums)中二分 子数组最大值是有范围的
        int left = 0;
        int right = 0;
        for(int num:nums) {
            right += num;
            left = num > left ? num : left;
        }
        while(left < right) {
            int mid = left + (right - left) / 2;
            int cnt = 1; //记录分成的组数
            int sum = 0;
            for(int num:nums) {
                if(sum + num > mid) {
                    sum = num;
                    cnt++;
                } else {
                    sum += num;
                }
            }
            if(cnt > m) {  //组数大于规定组数，证明mid小了，在右侧继续搜索
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        return left;
    }
}
 

几乎刷完了力扣所有的二分题，我发现了这些

前言

大家好，我是 lucifer。今天给大家带来的是《二分》专题。先上下本文的提纲，这个是我用 mindmap 画的一个脑图，之后我会继续完善，将其他专题逐步完善起来。

大家也可以使用 vscode blink-mind 打开源文件查看，里面有一些笔记可以点开查看。源文件可以去我的公众号《力扣加加》回复脑图获取，以后脑图也会持续更新更多内容。vscode 插件地址：marketplace.visualstudio.com/items?itemN…

本系列包含以下专题：

• 几乎刷完了力扣所有的链表题，我发现了这些东西。。。
• 几乎刷完了力扣所有的树题，我发现了这些东西。。。
• 几乎刷完了力扣所有的堆题，我发现了这些东西。。。（上）
• 几乎刷完了力扣所有的堆题，我发现了这些东西。。。（下）

本专题预计分两部分两进行。第一部分主要讲述基本概念 和 一个中心。有了这些基础知识之后，第二部分我们继续学习两种二分类型 和四大应用。

本文内容已经同步到我的刷题插件的 RoadMap 中，结合刷题插件食用味道更佳哦~ 插件的获取方式可以在我的公众号力扣加加中回复插件查看。

如果觉得文章有用，请点赞留言转发一下，让我有动力继续做下去。

前言

为了准备这个专题，我不仅肝完了力扣的所有二分题目，还肝完了另外一个 OJ 网站 - Binary Search 的所有二分题目，一共100 多道。大家看完如果觉得有用，可以通过点赞转发的方式告诉我，如果喜欢的人多，我继续尽快出下篇哦~

二分查找又称折半搜索算法。 狭义地来讲，二分查找是一种在有序数组查找某一特定元素的搜索算法。这同时也是大多数人所知道的一种说法。实际上， 广义的二分查找是将问题的规模缩小到原有的一半。类似的，三分法就是将问题规模缩小为原来的 1/3。

本文给大家带来的内容则是狭义地二分查找，如果想了解其他广义上的二分查找可以查看我之前写的一篇博文 从老鼠试毒问题来看二分法

尽管二分查找的基本思想相对简单，但细节可以令人难以招架 ... — 高德纳

当乔恩·本特利将二分搜索问题布置给专业编程课的学生时，百分之 90 的学生在花费数小时后还是无法给出正确的解答，主要因为这些错误程序在面对边界值的时候无法运行，或返回错误结果。1988 年开展的一项研究显示，20 本教科书里只有 5 本正确实现了二分搜索。不仅如此，本特利自己 1986 年出版的《编程珠玑》一书中的二分搜索算法存在整数溢出的问题，二十多年来无人发现。Java 语言的库所实现的二分搜索算法中同样的溢出问题存在了九年多才被修复。

可见二分查找并不简单， 本文就试图带你走近 ta，明白 ta 的底层逻辑，并提供模板帮助大家写书 bug free 的二分查找代码。看完讲义后建议大家结合 LeetCode Book 二分查找 练习一下。

基本概念

首先我们要知道几个基本概念。这些概念对学习二分有着很重要的作用，之后遇到这些概念就不再讲述了，默认大家已经掌握。

解空间

解空间指的是题目所有可能的解构成的集合。比如一个题目所有解的可能是 1,2,3,4,5，但具体在某一种情况只能是其中某一个数（即可能是 1，2，3，4，5 中的一个数）。那么这里的解空间就是 1,2,3,4,5 构成的集合，在某一个具体的情况下可能是其中任意一个值，我们的目标就是在某个具体的情况判断其具体是哪个。如果线性枚举所有的可能，就枚举这部分来说时间复杂度就是 O(n)O(n)。

举了例子：

如果让你在一个数组 nums 中查找 target，如果存在则返回对应索引，如果不存在则返回 -1。那么对于这道题来说其解空间是什么？

很明显解空间是区间 [-1, n-1]，其中 n 为 nums 的长度。

需要注意的是上面题目的解空间只可能是区间 [-1,n-1] 之间的整数。而诸如 1.2 这样的小数是不可能存在的。这其实也是大多数二分的情况。 但也有少部分题目解空间包括小数的。如果解空间包括小数，就可能会涉及到精度问题，这一点大家需要注意。

比如让你求一个数 x 的平方根，答案误差在 10^-610−6 次方都认为正确。这里容易知道其解空间大小可定义为 [1,x]（当然可以定义地更精确，之后我们再讨论这个问题），其中解空间应该包括所有区间的实数，不仅仅是整数而已。这个时候解题思路和代码都没有太大变化，唯二需要变化的是：

1. 更新答案的步长。 比如之前的更新是 l = mid + 1，现在可能就不行了，因此这样可能会错过正确解，比如正确解恰好就在区间 [mid,mid+1] 内的某一个小数。
2. 判断条件时候需要考虑误差。由于精度的问题，判断的结束条件可能就要变成 与答案的误差在某一个范围内。

对于搜索类题目，解空间一定是有限的，不然问题不可解。对于搜索类问题，第一步就是需要明确解空间，这样你才能够在解空间内进行搜索。这个技巧不仅适用于二分法，只要是搜索问题都可以使用，比如 DFS，BFS 以及回溯等。只不过对于二分法来说，明确解空间显得更为重要。如果现在还不理解这句话也没关系，看完本文或许你就理解了。

定义解空间的时候的一个原则是： 可以大但不可以小。因为如果解空间偏大（只要不是无限大）无非就是多做几次运算，而如果解空间过小则可能错失正确解，导致结果错误。比如前面我提到的求 x 的平方根，我们当然可以将解空间定义的更小，比如定义为 [1,x/2]，这样可以减少运算的次数。但如果设置地太小，则可能会错过正确解。这是新手容易犯错的点之一。

有的同学可能会说我看不出来怎么办呀。我觉得如果你实在拿不准也完全没有关系，比如求 x 的平方根，就可以甚至为 [1,x]，就让它多做几次运算嘛。我建议你给上下界设置一个宽泛的范围。等你对二分逐步了解之后可以卡地更死一点。

序列有序

我这里说的是序列，并不是数组，链表等。也就是说二分法通常要求的序列有序，不一定是数组，链表，也有可能是其他数据结构。另外有的序列有序题目直接讲出来了，会比较容易。而有些则隐藏在题目信息之中。乍一看，题目并没有有序关键字，而有序其实就隐藏在字里行间。比如题目给了数组 nums，并且没有限定 nums 有序，但限定了 nums 为非负。这样如果给 nums 做前缀和或者前缀或（位运算或），就可以得到一个有序的序列啦。

更多技巧在四个应用部分展开哦。

虽然二分法不意味着需要序列有序，但大多数二分题目都有有序这个显著特征。只不过：

• 有的是题目直接限定了有序。这种题目通常难度不高，也容易让人想到用二分。
• 有的是需要你自己构造有序序列。这种类型的题目通常难度不低，需要大家有一定的观察能力。

比如Triple Inversion。题目描述如下：

Given a list of integers nums, return the number of pairs i < j such that nums[i] > nums[j] * 3.

Constraints： n ≤ 100,000 where n is the length of nums
Example 1
Input：
nums = [7, 1, 2]
Output：
2
Explanation：
We have the pairs (7, 1) and (7, 2)

复制代码

这道题并没有限定数组 nums 是有序的，但是我们可以构造一个有序序列 d，进而在 d 上做二分。代码：

class Solution:
    def solve(self, A):
        d = []
        ans = 0

        for a in A:
            i = bisect.bisect_right(d, a * 3)
            ans += len(d) - i
            bisect.insort(d, a)
        return ans
复制代码

如果暂时不理解代码也没关系，大家先留个印象，知道有这么一种类型题即可，大家可以看完本章的所有内容（上下两篇）之后再回头做这道题。

极值

类似我在堆专题 提到的极值。只不过这里的极值是静态的，而不是动态的。这里的极值通常指的是求第 k 大（或者第 k 小）的数。

堆的一种很重要的用法是求第 k 大的数，而二分法也可以求第 k 大的数，只不过二者的思路完全不同。使用堆求第 k 大的思路我已经在前面提到的堆专题里详细解释了。那么二分呢？这里我们通过一个例子来感受一下：这道题是 Kth Pair Distance，题目描述如下：

Given a list of integers nums and an integer k, return the k-th (0-indexed) smallest abs(x - y) for every pair of elements (x, y) in nums. Note that (x, y) and (y, x) are considered the same pair.

Constraints:n ≤ 100,000 where n is the length of nums
Example 1
Input:
nums = [1, 5, 3, 2]
k = 3
Output:
2
Explanation:

Here are all the pair distances:

abs(1 - 5) = 4
abs(1 - 3) = 2
abs(1 - 2) = 1
abs(5 - 3) = 2
abs(5 - 2) = 3
abs(3 - 2) = 1

Sorted in ascending order we have [1, 1, 2, 2, 3, 4].
复制代码

简单来说，题目就是给的一个数组 nums，让你求 nums 第 k 大的任意两个数的差的绝对值。当然，我们可以使用堆来做，只不过使用堆的时间复杂度会很高，导致无法通过所有的测试用例。这道题我们可以使用二分法来降维打击。

对于这道题来说，解空间就是从 0 到数组 nums 中最大最小值的差，用区间表示就是 [0, max(nums) - min(nums)]。明确了解空间之后，我们就需要对解空间进行二分。对于这道题来说，可以选当前解空间的中间值 mid ，然后计算小于等于这个中间值的任意两个数的差的绝对值有几个，我们不妨令这个数字为 x。

• 如果 x 大于 k，那么解空间中大于等于 mid 的数都不可能是答案，可以将其舍弃。
• 如果 x 小于 k，那么解空间中小于等于 mid 的数都不可能是答案，可以将其舍弃。
• 如果 x 等于 k，那么 mid 就是答案。

基于此，我们可使用二分来解决。这种题型，我总结为计数二分。我会在后面的四大应用部分重点讲解。

代码：

class Solution:
    def solve(self, A, k):
        A.sort()
        def count_not_greater(diff):
            i = ans = 0
            for j in range(1, len(A)):
                while A[j] - A[i] > diff:
                    i += 1
                ans += j - i
            return ans
        l, r = 0, A[-1] - A[0]

        while l <= r:
            mid = (l + r) // 2
            if count_not_greater(mid) > k:
                r = mid - 1
            else:
                l = mid + 1
        return l
复制代码

如果暂时不理解代码也没关系，大家先留个印象，知道有这么一种类型题即可，大家可以看完本章的所有内容（上下两篇）之后再回头做这道题。

一个中心

二分法的一个中心大家一定牢牢记住。其他（比如序列有序，左右双指针）都是二分法的手和脚，都是表象，并不是本质，而折半才是二分法的灵魂。

前面已经给大家明确了解空间的概念。而这里的折半其实就是解空间的折半。

比如刚开始解空间是 [1, n]（n 为一个大于 n 的整数）。通过某种方式，我们确定 [1, m] 区间都不可能是答案。那么解空间就变成了 (m,n]，持续此过程知道解空间变成平凡（直接可解）。

注意区间 (m,n] 左侧是开放的，表示 m 不可能取到。

显然折半的难点是根据什么条件舍弃哪一步部分。这里有两个关键字:

1. 什么条件
2. 舍弃哪部分

几乎所有的二分的难点都在这两个点上。如果明确了这两点，几乎所有的二分问题都可以迎刃而解。幸运的是，关于这两个问题的答案通常都是有限的，题目考察的往往就是那几种。这其实就是所谓的做题套路。关于这些套路，我会在之后的四个应用部分给大家做详细介绍。

二分法上篇小结

上篇主要就是带大家了解几个概念，这些概念对做题极为重要，请务必掌握。接下来讲解了二分法的中心 - 折半，这个中心需要大家做任何二分都要放到脑子中。

如果让我用一句话总结二分法，我会说二分法是一种让未知世界无机可乘的算法。即二分法无论如何我们都可以舍弃一半解，也就是无论如何都可以将解空间砍半。难点就是上面提到的两点：什么条件 和 舍弃哪部分。这是二分法核心要解决的问题。

以上就是《二分专题（上篇）》的所有内容。如果觉得文章有用，请点赞留言转发一下，让我有动力继续出下集。

下集预告

上集介绍的是基本概念。下一集我们介绍两种二分的类型以及四种二分的应用。

下集目录：

• 两种类型

  • 最左插入

  • 最右插入

• 四大应用

  • 能力检测二分

  • 前缀和二分

  • 插入排序二分（不是你理解的插入排序哦）

  • 计数二分

其中两种类型（最左和最右插入）主要解决的的是：解空间已经明确出来了，如何用代码找出具体的解。

而四大应用主要解决的是：如何构造解空间。更多的情况则是如何构建有序序列。

这两部分都是实操性很强的内容，在理解这两部分内容的同时，请大家务必牢记一个中心折半。那我们下篇见喽~

以上就是本文的全部内容了， 大家对此有何看法，欢迎给我留言，我有时间都会一一查看回答。我是 lucifer，维护西湖区最好的算法题解，Github 超 40K star 。大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。