晓龙oba

算法与数据结构 - 二分查找详解

文章目录

前言
一、引言
二、场景模拟
- 2.1 笨蛋式猜测方法（穷举）
- 2.2 二分查找
三、二分查找介绍
- 3.1 理论概念（面试八股文）
- 3.2 二分查找的查找过程（原理）
四、二分查找实现详解
- 4.1 基本二分查找
- - 思路
  - 实战一
- 4.2 查找元素的第一个和最后一个位置（判断区间的左右边界）
- - 实战二
- 4.3 寻找第一个错误版本（判断区间的左侧边界）
- - 实战三
五、二分查找的时间复杂度
结语

前言

点赞再看，养成习惯！

关注晓龙oba公众号,更多电子书及学习资源免费领取。

一、引言

相信很多小伙伴都和朋友做过一个小互动：

今天李雷和韩梅梅一起相约去逛街，期间李雷发现韩梅梅穿了一双限量款的球鞋。
李雷：韩同学，你这双鞋好漂亮哦，在哪里买的呢？
韩梅梅：这是我在莆田的网友卖给我的，物美价廉。
李雷：多少钱呢？
韩梅梅： 你猜！

二、场景模拟

已知：该款球鞋在某平台正版售价为2000元，莆田网友售价一定小于正版价格。

2.1 笨蛋式猜测方法（穷举）

最近盗版脑白金喝多的李雷同学不假思索地从1块钱开始猜:

李雷： 1块
韩梅梅：不对，少了
李雷： 2块
韩梅梅：不对，少了
… long long time ago …
李雷：250
韩梅梅：对了！（鄙视脸）

同样，我们用程序模拟一下这个过程：

public class SimpleBinarySearch {
    public static void main(String[] args) {
        Integer max_price = 2000;
        Integer real_price = 250;
        Integer count = guessCounts(max_price, real_price);
        System.out.println(count);
    }

    private static Integer guessCounts(Integer max_price, Integer real_price) {
        Integer counts = 0;
        Integer guess_price = 0;
        for (int i = 0; i < max_price; i++) {
            counts++;
            guess_price++;
            if (guess_price.equals(real_price) ) {
                break;
            }
        }

        return counts;
    }
}

这里李雷猜测了250次终于猜出了结果，但是给人一种很笨的感觉，那么我们有没有更好的办法呢？

2.2 二分查找

如果李雷喝的是正版脑白金，他会如何猜测呢？

李雷： 1000元？
韩梅梅：不对，贵了
李雷： 500元？
韩梅梅：不对，贵了
李雷： 250元？
韩梅梅：对了呢，李雷你好棒哦♥

同样，我们用程序来模拟下这个过程（这里简单看下就好，后面会详细的讲实现思路）：

public class SimpleBinarySearch {
    public static void main(String[] args) {
        Integer max_price = 2000;
        Integer real_price = 250;
        Integer count = guessCounts(max_price, real_price);
        System.out.println(count);
    }

    private static Integer guessCounts(Integer max_price, Integer real_price) {
        /*该变量为了统计计算次数，不参与二分查找运算过程*/
        Integer counts = 0;
        /*下面是二分查找的细节实现*/
        Integer min_price = 0;
        while (min_price <= max_price) {
            counts++;
            int guess_price = min_price + (max_price - min_price) / 2;
            if (guess_price == real_price) {
                break;
            } else if (guess_price < real_price) {
                min_price = guess_price;
            } else if (guess_price > real_price) {
                max_price = guess_price;
            }
        }
        return counts;
    }
}

三、二分查找介绍

3.1 理论概念（面试八股文）

二分查找也叫做折半查找，是一种双高的查找算法（效率高，面试提问率高）。但是使用二分查找有个大前提条件：我们查找的目标线性表必须是有序存储结构且其排序方式是按照我们查找关键词进行排序。

3.2 二分查找的查找过程（原理）

就像我们刚刚举的例子一样，二分查找首先需要我们的目标元素是有序的，并且其排序依据是按照我们的排序关键词进行的。我们每次查找的时候讲元素一分为二组成前后两张表，如果中间位置的记录大于我们的关键字则继续进行这一操作，直到我们查找到目标元素位置或者无法继续拆分为止。
这里我们有两个重点：

必须是有序线性表
必须是按照查找关键字排序

简单概括其行为就是：

在一个有序的线性表中，每次将表等分两部分并将目标元素与表的中间元素进行比较
如果等于中间元素，则返回中间元素的位置
若小于中间元素则在小于中间元素的部分中重复步骤1
若大于中间元素则在大于中间元素的部分中重复步骤1
重复上述步骤直到找到目标元素或无法再拆分表为止

四、二分查找实现详解

4.1 基本二分查找

思路

最基本的二分查找通常就是判断线性表中是否存在元素或者某元素在线性表中的位置，通常针对这种需求,我们可以将刚刚讲过的二分查找过程转换为代码:

    public static int simpleBinarySearch(int[] nums, int target) {
        Integer max_value = nums.length - 1;// 注意点一
        Integer min_value = 0;
        while (min_value <= max_value) {//注意点二
            int mid_value = min_value + (max_value - min_value) / 2; //注意点三
            if (nums[mid_value] == target) {
                return mid_value;
            } else if (nums[mid_value] < target) {
                min_value = mid_value+1;//注意点四
            } else if (nums[mid_value] > target) {
                max_value = mid_value-1;//注意点五
            }
        }
            return -1 ; // 表示未找到
    }

这里我们重点讲解下注意点:
注意点一：这里我们的最大值取得是数组长度减一,即nums.length - 1;,这是为了防止数组越界。不过这也造成了我们针对于数组下标的取值空间变为了：[0 , nums.length-1] ，闭区间。
注意点二：这里会有小伙伴问为什么这里min_value <= max_value 小于等于 而不是小于？这个其实也很简单，因为我们的取值为[0 , nums.length-1] 闭区间而非[0 , nums.length)开区间，这里为了避免[3,3]这种闭区间出现，此时最小值与最大值虽然相等，但是此时区间内还是存在元素3而非空集合，因此不应该跳出循环判断。
注意点三：min_value + (max_value - min_value) / 2的效果等于(min_value+max_value)/2，但是避免了因为min_value+max_value潜在可能造成的类型溢出问题。
注意点四：这里是min_value = mid_value+1而非min_value = mid_value也是由于我们需求的是闭区间，而mid_value这个值不应该存在于我们的集合空间中。
注意点五：同四

实战一

口说无凭，让我们做一道题练习下：

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/search-insert-position

题目分析：
这里和我们刚刚提到的基础案例只有一点点的小区别：我们基础案例中如果没有找到元素返回的是-1，但是此题中要求我们如果没有找到元素将按照排序返回它插入的位置，因此我们只需要做一点小的修改即可：

    public static int simpleBinarySearch(int[] nums, int target) {
        Integer max_value = nums.length - 1;
        Integer min_value = 0;
        while (min_value <= max_value) {
            int mid_value = min_value + (max_value - min_value) / 2; 
            if (nums[mid_value] == target) {
                return mid_value;
            } else if (nums[mid_value] < target) {
                min_value = mid_value+1;
            } else if (nums[mid_value] > target) {
                max_value = mid_value-1;
            }
        }
            return min_value ; // 注意点一
    }

注意点一：这里是唯一变动的地方，为什么我们会返回min_value呢？我们就以nums=[1, 3, 4, 5]，target=2举例：
我们先来看第一次取值过程：

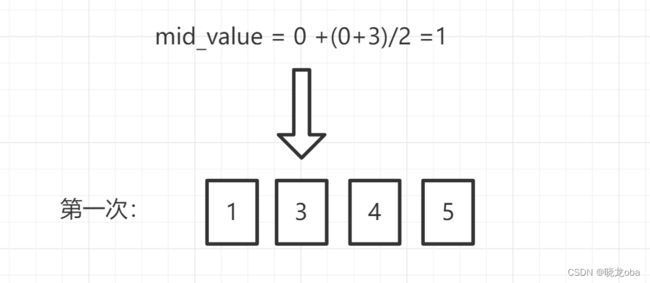
此时我们取得mid_value = 1，对应数组中的元素就是3。我们拿取到的元素3去和我们的目标值target=2进行比较：

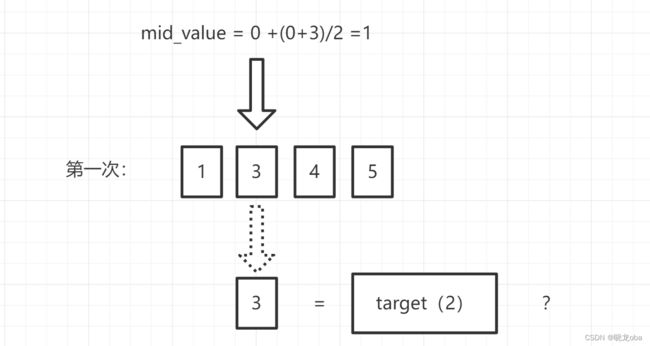
比较结果显而易见，元素3并不等于我们的目标值2，因此我们的代码会继续向下进行大小判断

            } else if (nums[mid_value] < target) {
                min_value = mid_value+1;
            } else if (nums[mid_value] > target) {
                max_value = mid_value-1;
            }

显而易见的，这里的元素3要大于我们的目标值2，因此会执行 max_value = mid_value-1;此时我们将要进行第二次循环：

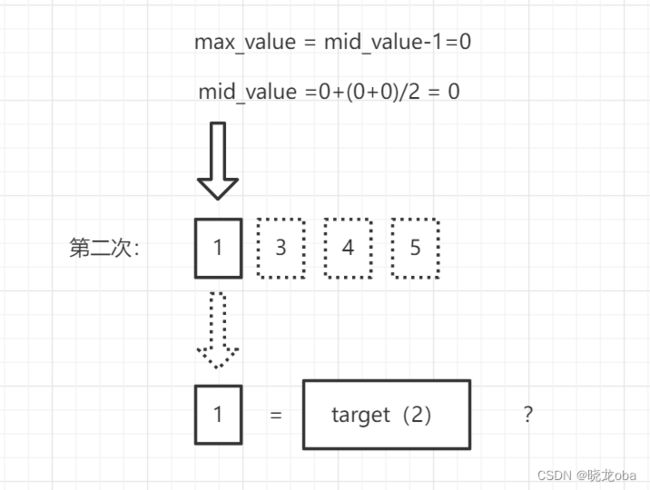
此时我们取得mid_value = 0，对应数组中的元素就是1。我们拿取到的元素1去和我们的目标值target=2进行比较,结果显而易见，1<2，此时按照逻辑会执行min_value = mid_value+1;，此时min_value = 1
这里重点来了 ，此时我们之前一直没有提到的循环进入判断的代码发挥了作用： while (min_value <= max_value)，由于此时的min_value = 1,max_value=0，无法满足循环的进入条件，代码向下进行并返回min_value=1。按照运算结果得到：

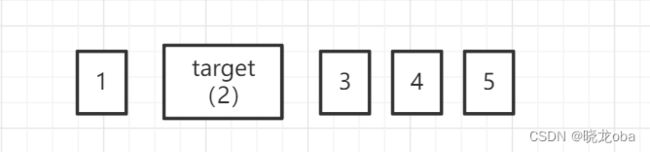
符合我们的预期结果。
这里用图像演示了一次程序的运行过程，可能还有小伙伴并不是很清楚。其实我们上述的代码无非只有两种可能：

第一种：查找到目标元素并成功地返回下标
第二种：无法找到目标元素，此时需要查找到该元素的插入位置。

此时我们需要考虑的主要就是第二种情况，而第二种情况在进行多次比较后一定会进入一个由单个元素组成的闭区间，此时无非就只有两种情况，我的闭区间唯一元素小于目标元素，目标元素需要插入到唯一元素的右侧，此时代码判断进入：

else if (nums[mid_value] < target) {
                min_value = mid_value+1;
 }

符合我们想要插入最小值右侧的预期。
第二种情况就是唯一区间元素大于目标元素，我们希望目标元素插入到最小值位置，此时代码进入：

else if (nums[mid_value] > target) {
                max_value = mid_value-1;
}

此时min_value的值不会发生变化，依旧符合我们对于程序运行的预期。

附上我们程序的运行结果：

4.2 查找元素的第一个和最后一个位置（判断区间的左右边界）

实战二

我们先来看下题目:

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值 target，返回 [-1, -1]。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array

思路
这一题是实战一题目的进阶版本,实战一更多的是让我们判断元素是否存在,而本题更多的则是让我们可以更加灵活地控制头尾指针的适用。
这道题有很多种解法，咱们说一种比较简单能够想到的的：
我们还是按照惯例寻找数组中是否存在我们需要的元素，如果不存在则返回[-1，-1]，若是存在的话，我们就以当前坐标作为基坐标，向前和向后去寻找元素第一次出现和最后一次出现的位置（这里是依据元素是有序排列，因此相同元素必是连续的）。
代码：

    public int[] searchRange(int[] nums,int target){
        Integer max_index = nums.length -1 ;
        Integer min_index = 0 ;
        while (min_index <= max_index){
            int  mid_index = min_index +(max_index - min_index)/2 ;
            if(nums[mid_index] == target){
                // 此时获取到元素值  判断元素前后指针的值
                min_index = mid_index ;
                max_index = mid_index ;
                while(min_index-1 >= 0 &&nums[min_index-1] == target){
                    min_index -- ;
                }
                while (max_index+1 <= nums.length -1 &&nums[max_index+1] == target){
                    max_index ++ ;
                }
                return new int[]{min_index,max_index} ;
            }
            else if (nums[mid_index] < target){
                min_index = mid_index + 1 ;
            }
            else if(nums[mid_index] > target) {
                max_index = mid_index - 1;
            }
        }
        return new int[]{-1, -1};
    }

运行结果：

其实这题还可以分别去寻找元素第一次出现即最后一次出现的位置，这个解法就留做课后题给小伙伴们思考。

4.3 寻找第一个错误版本（判断区间的左侧边界）

实战三

这道题就是二分查找中面试最长见到的一道题：

你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, …, n]，你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/first-bad-version

思路：
本题依旧没有摆脱二分查找的常见框架，是很典型的在阅读题目的时候就能够想到需要使用二分查找解决的题型。与经典题型相比，该题的变化是当元素值大于等于元素值时返回的结果都是true，而仅有小于的时候返回的是false，我们需要做的就是寻找到第一次出现true的位置。我们将本题的解题步骤拆解开：
第一步：确认最大指针和最小指针分别是什么。本体里由于我们的序列不再是数组结构，而是从1开始的连续数字，因此我们可以将最小指针指向1，最大指针指向我们传入的值。
第二步：确认我们循环的终止条件，这里面由于我们采用的是[1,version]的闭区间，因此终止条件一九可以沿用min_value <= max_value 。
第三步：确认我们缩小二分区间的逻辑。这里其实有两种方式：

第一种，当我们确认当前版本是错误版本时左移一位校验是否为正确版本，如果是则返回，如果不是则将右侧max_value指针左移。如果当前版本是正确版本，则直接将min_value指针右移。
第二种，当我们当前版本是错误版本时，贼将max_value指针左移到当前位置，否则将min_value指针右移到当前位置，但是由于这种方式采用的是开区间，因此while条件则为 while (left < right)

第一种代码实现：

private static int firstBadVersion(int n) {
        Integer min_value = 1 ;
        Integer max_value = n ;
        while (min_value <= max_value){
            int mid_value = min_value +(max_value - min_value) /2 ;
            if (isBadVersion(mid_value)){
                if(!isBadVersion(mid_value-1)){
                    return mid_value;
                }
                max_value = mid_value -1 ;
            }
            else {
                min_value = mid_value +1 ;
            }
        }
        return min_value ;
    }

运行结果

第二种代码实现：

// 其实我第一时间没想到第二种题解，但是在运行程序的时候发现了我一年前写的这种题解，哈哈哈哈
   public int firstBadVersion(int n) {
        int left = 1, right = n;
        while (left < right) { // 循环直至区间左右端点相同
            int mid = left + (right - left) / 2; // 防止计算时溢出
            if (isBadVersion(mid)) {
                right = mid; // 答案在区间 [left, mid] 中
            } else {
                left = mid + 1; // 答案在区间 [mid+1, right] 中
            }
        }
        // 此时有 left == right，区间缩为一个点，即为答案
        return left;
    }