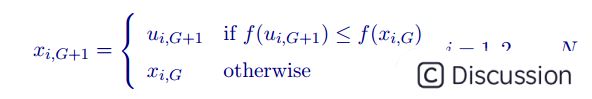【优化求解】差分进化算法（Differential Evolution)matlab源码

差分进化算法DE属于进化算法，这里算法还包括依次遗传算法、进化策略、进化规划。

差分进化算法包括三个基本的操作：变异操作、交叉(重组)操作和选择操作。

一、算法建模：

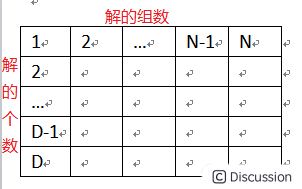
1、假设我们希望得到函数f(x)的最优解，这个函数有D个解。\ 2、为函数f(x)设置一个解的组数N，N至少为4。\ 3、这样我们就得到了N组并且每组解的个数为D的集合，它可以使用N个D维参数向量来表示。\ \ 因为它类似于遗传算法进化一样，是一代一代的进行进化，最终得到最优个体。所以上面G表示的就是代数。

形象表示如下：\

二、初始化

为每个参数定义上界和下界\ \ 在上面的范围内随机的为每个参数取值。这样就得到了一个N组初始解。

三、变异\

上面有N组解，对于一组给定的解X(i,G)随机的从这N组解中选择三组解X(r1,G)，X(r2,G)，X(r3,G)，r1，r2，r3分别代表组的索引，G表示代数，从第一代开始。

使用下面变异策略进行变异：\

其中，F是变异因子，位于[0,2]之间。这样我们就可以得到一组新的解。

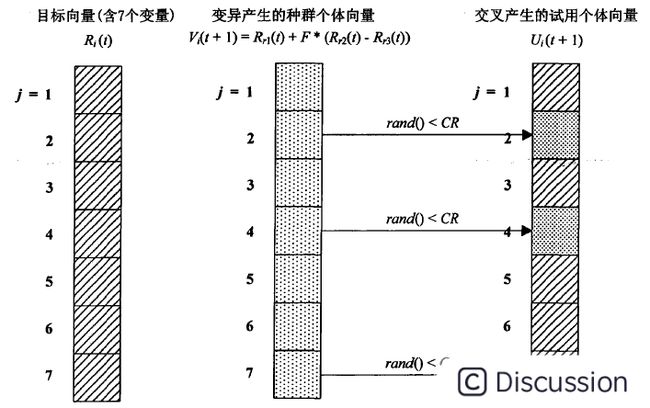
四、交叉

下面我们就会对得到的这组新解进行交叉操作了。

CR是交叉概率，处于[0, 1]之间。

五、选择

从上面可以得到一组进化之后的解，为了决定这组解是否成为G+1代中的解，需要将这组新解跟原来那组解的适应度值进行比较，如果优于原来那组解则将它们替换掉，否则保留原来解。适应度值得计算使用的就是适应度函数f(x)。这个函数需要我们之前进行确定。

整个过程的流程图如下：

``` function demo1 %DEMO1 Demo for usage of DIFFERENTIALEVOLUTION.

% Set title optimInfo.title = 'Demo 1 (Rosenbrock''s saddle)';

% Specify objective function objFctHandle = @rosenbrocksaddle;

% Define parameter names, ranges and quantization:

% 1. column: parameter names % 2. column: parameter ranges % 3. column: parameter quantizations % 4. column: initial values (optional)

paramDefCell = { 'parameter1', [-3 3], 0.01 'parameter2', [-3 3], 0.01 };

% Set initial parameter values in struct objFctParams objFctParams.parameter1 = -2; objFctParams.parameter2 = 2.5;

% Set single additional function parameter objFctSettings = 100;

% Get default DE parameters DEParams = getdefaultparams;

% Set number of population members (often 10*D is suggested) DEParams.NP = 20;

% Do not use slave processes here. If you want to, set feedSlaveProc to 1 and % run startmulticoreslave.m in at least one additional Matlab session. DEParams.feedSlaveProc = 0;

% Set times DEParams.maxiter = 20; DEParams.maxtime = 30; % in seconds DEParams.maxclock = [];

% Set display options DEParams.infoIterations = 1; DEParams.infoPeriod = 10; % in seconds

% Do not send E-mails emailParams = [];

% Set random state in order to always use the same population members here setrandomseed(1);

% Start differential evolution [bestmem, bestval, bestFctParams, nrOfIterations, resultFileName] = differentialevolution(... DEParams, paramDefCell, objFctHandle, objFctSettings, objFctParams, emailParams, optimInfo); %#ok

disp(' '); disp('Best parameter set returned by function differentialevolution:'); disp(bestFctParams);

% Continue optimization by loading result file if DEParams.saveHistory

disp(' '); disp(textwrap2(sprintf(... 'Now continuing optimization by loading result file %s.', resultFileName))); disp(' ');

DEParams.maxiter = 100; DEParams.maxtime = 60; % in seconds

[bestmem, bestval, bestFctParams] = differentialevolution(... DEParams, paramDefCell, objFctHandle, objFctSettings, objFctParams, emailParams, optimInfo, ... resultFileName); %#ok

disp(' '); disp('Best parameter set returned by function differentialevolution:'); disp(bestFctParams); end ```

​