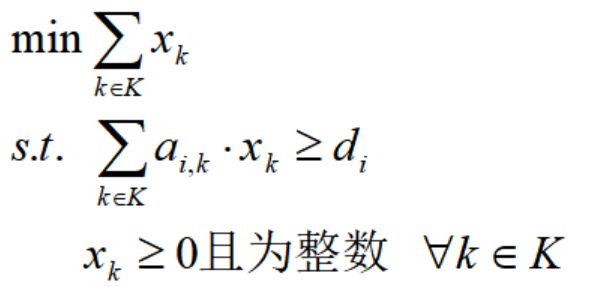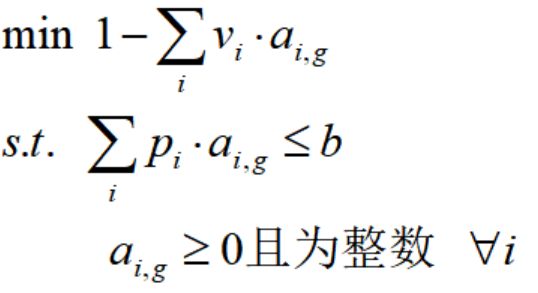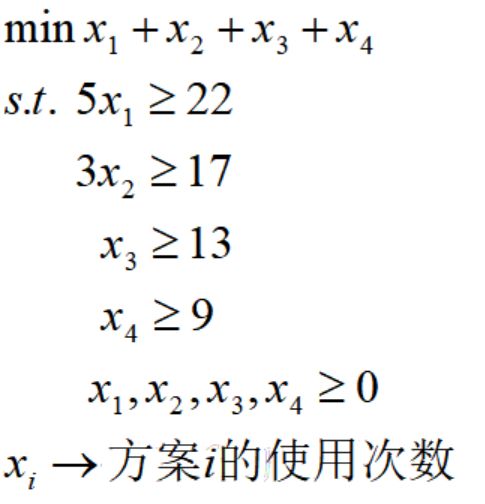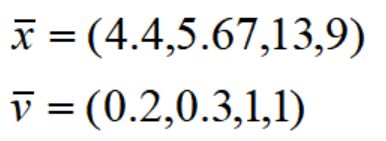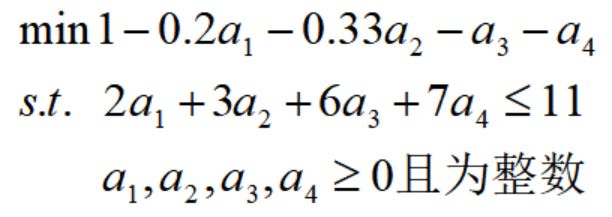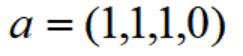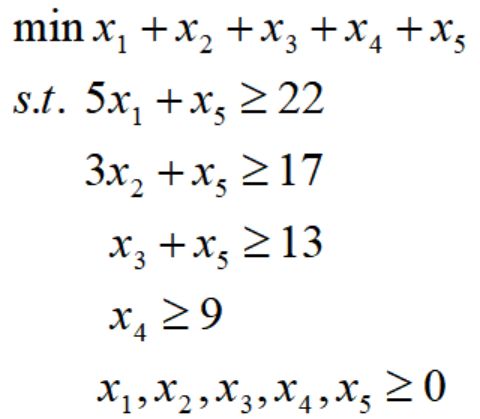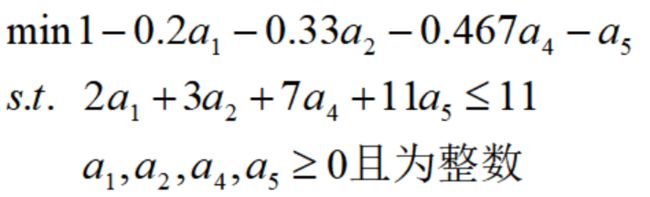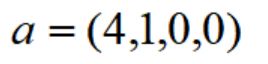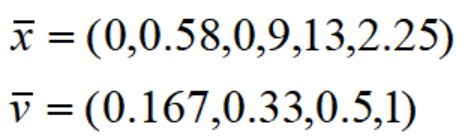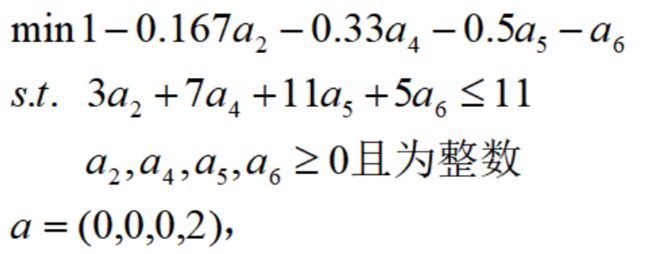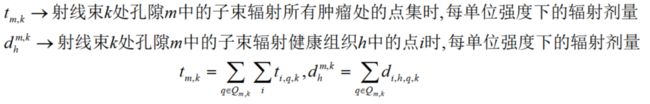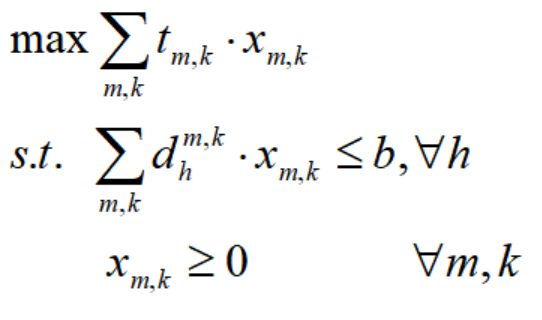大规模优化方法(一)
迄今为止,我们介绍的优化算法都是从整体性出发,搜索全局最优点。而且大多数都是从一个初始可行解出发进行的(分支定界搜索从某种意义上可以说不是)。换句话,这些算法都是直接求解。但一些问题过于复杂,要优化的变量实在过多,规模庞大,以至于没办法从整体考虑入手。今天我们介绍间接求解的算法,将原问题分解成多个足够简单、可以单独迭代直接求解的子问题(subproblem),伴随的主问题(master problem)结合所有子问题的结果给出模型的精确或近似最优解。话不多说,进入正题。
1
列生成算法
首先要介绍的是列生成算法,我们在介绍离散优化模型的分类时提到过(集合包装、覆盖、划分模型)。
传送门:离散优化模型
列生成算法适用于满足以下特点的优化问题:
该问题对应的数学模型能够简单地使用约束矩阵中每一个可能的列来表示决策变量的选择,这些可行的列是通过一个独立子问题构造生成,同时能够满足即便是那些难以用模型表达的复杂约束条件。
列生成算法的思想是基于给定生成的列,通过迭代求解限制主问题(partial master problem)实现全局优化——这里的主问题是指受限原始问题(restricted version),只包含了取值非零的决策变量对应的列。如果原始问题的模型是一个整数线性规划问题,则可以求解受限问题的线性松弛问题。其算法数学表达为:
我们给出列生成算法的一般步骤:
对偶问题在前面以及详细介绍过,传送门:线性规划的对偶理论
该算法最难实现的部分是步骤2中如何构造小于0的检验数,一个方法就是把J的所有列拿出来逐个尝试,但效率无疑是低下的。我们可以采取启发式算法,只要判断所有可行列中最小检验数是否小于0即可。
我们通过一个案例来了解该算法——家具型材切割。
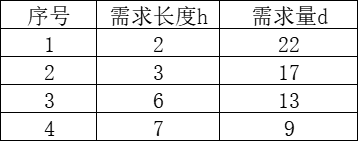
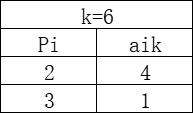
家具制造所需要的型材都是从长度为b=11米的进料中切割下来的,现需要如下表所示的不同长度的型材,制造商应该如何下料使得满足需求的同时用料最省?
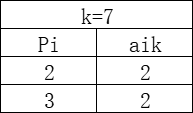
首先,定义切割方案k为一个总长度不超过b米,带有不同长度(pi)型材的切割数量(aik)的组合。设K表示所有可能的切割方案构成的集合,xk表示切割方案k使用的次数,那么下料问题可描述为如下整数规划问题:
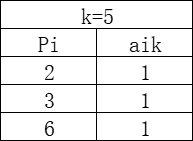
我们这里要理解一下,方案k是对长度不超过11米的型材进行切割,切成不同的组合,比如下面展示的一些组合:
而大K表示满足需求的切割方案构成的集合,比如它的一个元素可以是:
上面这个元素也是构造初始限制主问题最简便的切割方案(4种只切割单一长度型材的方案)。根据算法步骤2,对模型的当前限制主问题l,求解其线性松弛问题可得到最优对偶解{vi},那么下一个生成列p可以通过求解背包问题得到:
下面我们执行列生成算法。首先,用最简便切割方案得到初始主限制问题:
得到最优解(目标值为32):
然后进入步骤2,构造背包问题:
得到最优解:
加入新的切割方案:
回到步骤1,求解新的规划问题:
最优解为(目标值25.13):
然后进入步骤2,构造背包问题:
得到最优解(目标值小于0):
加入新切割方案:
回到步骤1,求解新的规划问题,得到最优解(目标值24.83):
进入步骤2,构造背包问题,得到最优解(目标值-1):
加入新切割方案:
回到步骤1,重新计算规划问题,最优解此时不变。没有新的决策列加入。因此我们得到近似解:
可以看到,列生成算法适用于解决一类候选决策方案可以由多个完全信息下的列表示的组合优化问题。该算法并不是直接对带有所有列的规划问题进行求解,而是通过限制主问题求解只包含当前生成的列的模型,再由列生成子问题选择可能改进限制主问题目标函数值的列,并加入到限制主问题中。该算法的优点在于最后没有被子问题生成的列被判定为不会改进限制主问题的当前最优解,所以避免了考虑大量可能的列。
来到家居型材切割案例,就是事先不用把所有可能的切割方案列出来。列生成算法是解决大规模优化问题的重要思想,为了加深理解。我们再举一个案例——适型调强放射治疗(IMRT)的计划优化。
放射型治疗的目标是以最强的辐射消除肿瘤,但还需要尽量减少对周围正常组织的辐射以避免对它们的损伤。放疗采用的设备是一个大型加速器,它能够从人体周围的不同角度输出射线束,从而不仅可以对肿瘤病变靶区施加较高的辐射剂量,还可以使周围正常组织尽量少受辐射。由于加速器输出的射线束一般较大,因此,适型调强放射治疗(intensity modulated radiation therapy,IMRT)会结合许多不同照射强度的子束组成一个射线束,以提高治疗计划的精度。
子束是虚拟的,并不是物理真实存在的,它们通过借助一台带有移动叶片的多叶光栅将辐射剂量限制在一个开放的孔隙中,聚焦产生辐射作用(如下图)。不同子束的汇聚辐射作用如同条形图一样叠加,最后在不同角度射出。
并不是每一种子束的组合都能形成一个有效的孔隙。在一些限制条件下,只能通过移动两个边界之间的叶片才能产生有效缝隙;若在关闭“开口”或在类似图b第2行的中间区域,则不可能产生子束。若出现类似图c第2行和第3行的叶片重叠,则会引发“碰撞风险”,也不能形成有效的缝隙。
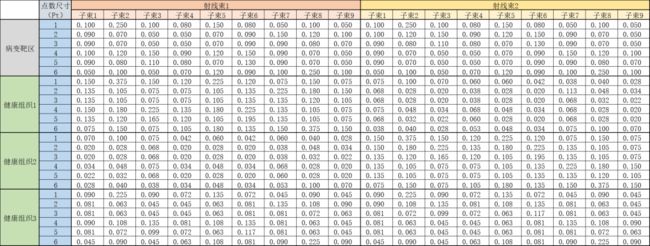
每一个器官组织由一个离散的点集表示,放疗计划优化的目标是最大化病变靶区的总辐射剂量(或者每个点的平均辐射剂量),约束条件是健康组织每个点接收到的总辐射剂量不得超过安全水平。输入参数估计了每单位强度下组织上每个点受到的子束辐射剂量:
下表给出了一个含有2个射线束、18个子束、12个点的实例,3个健康组织处最高辐射剂量的安全水平分别是b={50,65,70}
一旦选择来自射线束k处的孔隙m的子束集合Qm,k,那么可得:
由此可得到该案例的线性规划模型:
初始解可令两个射线束的所有子束均打开。
2
分支定价算法
可以看到,使用列生成算法常常将整数和小数解都保留在列生成子问题中,我们可以对限制主问题对应的线性松弛问题最优解取整很容易得到主问题的近似最优解。然而在许多实际问题中,由于决策变量是0-1整数变量,限制主问题的求解会变得非常复杂,即使取整也不能保证得到近似最优解。因此,我们需要用到分支定界搜索的枚举思想,结合列生成算法的思想,得到一种解决该问题的分支定价算法(branch and price):
我们通过一个实例来了解这个算法:
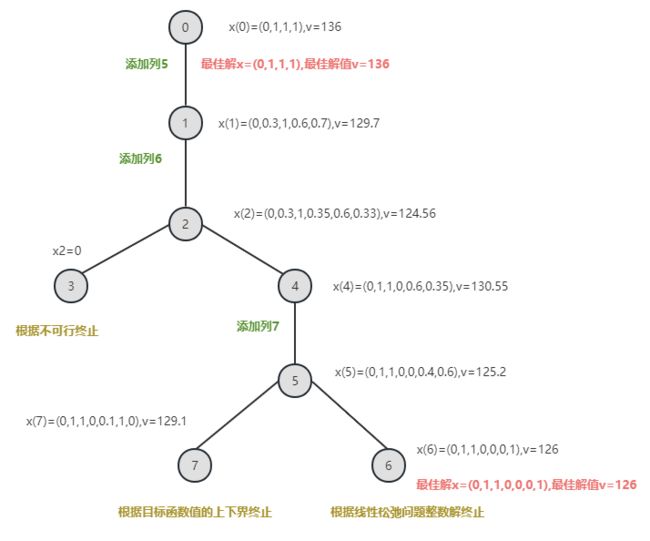
假设原问题是求最小化目标的0-1整数规划,初始化时,选择了四列构成规划问题的约束,得到根节点和初始解x(0),恰好是一个整数解,将最优解和对应的最优解更新。
然后下面重复步骤2~步骤4两次,第一次添加列5,得到线性松弛问题的解x(1),不满足0-1整数约束,进入步骤4,再次选择添加列6,得到新的解x(2),此时找不到满足条件的新列j。由于最优解124.56小于目前的最佳解136,不能马上停止该分支。进行分支,假设取分量2取整0,得到节点3不再满足整数约束,于是不可行终止。而取整1的分支4最优解为x(4),最优解值为130.55,此时又加入了列7得到节点5的最优解。最后得到分支6(取整分量是7),最优解满足0-1整数规划。所以终止分支。