分布式系统（交互、协作）

进程组织

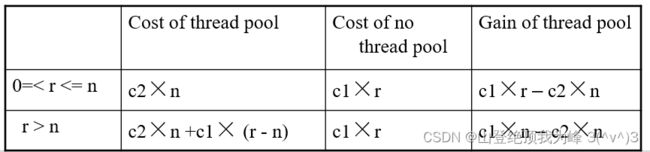
分布式系统的基本模块是进程（每台计算机上一个进程）。由于进程的执行过程分为执行和 I/O，因此每个进程中创建多个线程可以掩盖一部分的 I/O 延迟。然而，线程的创建开销较高。可以采取线程池技术，节省创建开销，但带来了管理开销。

1. 线程的创建开销：主要是内存分配，时间开销记为 $c_1$

2. 线程池维护开销：主要是线程的上下文切换，时间开销为 $c_2$

假设线程池大小为 $n$，实际系统中的并发数为 $r$（服从分布 $f(r)$ 的随机数，$p(r)$ 是其概率密度），那么：

因此预期收益为：
$$E(n)=\sum _{r=0}^n(c_{1}r-c_{2}n)f(r)+\sum _{r=n+1}^{\infty }(c_{1}n-c_{2}n)f(r)$$

把它连续化：
$$E(n)={\int }_0^n(c_{1}r-c_{2}n)p(r)dr+{\int }_n^{\infty }(c_{1}n-c_{2}n)p(r)dr$$

求导等于零，令 $\xi =c_2/c_1$，记 $n^{\ast }$ 是最佳线程池大小，那么
$${\int }_0^{\lfloor n^{\ast }\rfloor }p(r)dr\le 1-\xi <{\int }_0^{\lfloor n^{\ast }+1\rfloor }p(r)dr$$

如果知道 $c_1,c_2,p(r)$，那么就可以求出 $n^{\ast }$ 了。对于 $N$ 个用户的均匀分布 $Uniform(0,N)$，得到
$$\frac{\lfloor n^{\ast }\rfloor }{N}\le 1-\xi <\frac{1+\lfloor n^{\ast }\rfloor }{N}$$

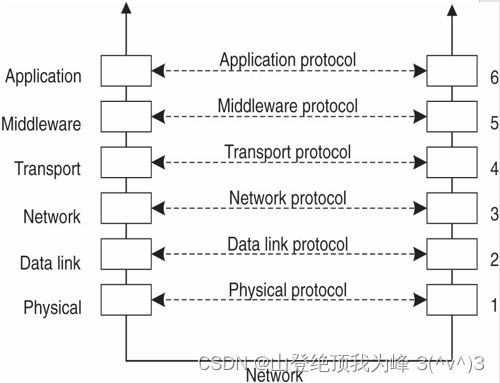
进程交互

分布式系统中的数据传递：overlay network（网络结构的某一层上虚拟网络）

• 应用层点对点方式
• 应用层多播、组播方式
• 应用层广播方式

传染病协议

Epidemic Protocol：一种在大规模分布式系统中，仅使用本地信息，就可以快速传播消息的方法。

节点状态：

1. 易感（susceptible）：还没被感染的节点，可以被其他节点感染
2. 感染（infective）：被感染的节点，会继续感染周边的其他节点
3. 移除（removed）：已经被感染的节点，不再感染其他节点，也不会再次感染

用途：故障检测、数据聚合、资源发现、监测、数据库复制。

反熵（Anti-Entropy）

节点 $P$ 随机地选择一个节点 $Q$，与它交换更新（exchanges updates），有三种方式：

1. Push：$P$ 把自己的更新推送给 $Q$（适合长时间不更新的系统，交换信息很浪费）
   1. $P\to Pnew(key,value,version)\to Q$
2. Pull：$P$ 从 $Q$ 拉取对方的更新（适合长时间不调用的系统，更新了数据也不使用）
   1. $P\to Pnew(key,version)\to Q$
   2. $Q\to Qnew(key,value,version)\to P$
3. Push-Pull：$P$ 和 $Q$ 互相发送更新
   1. $P\to Pnew(key,version)\to Q$
   2. $Q\to Qnew(key,value,version),PnewerQ(key,version)\to P$
   3. $P\to Pnew(key,value,version)\to Q$

这是一个简单（Simple）传染病协议，只包含易感、感染两种状态。我们定义轮（round）为：每个节点都至少与至少一个随机选择的节点交换更新的时间段。令 $p_i$ 是第 $i$ 轮的易感进程的占比，

• 使用 Pull 方式：这个易感进程随机挑选的进程，是个易感进程，拉取后不被感染，$p_{i+1}=p_i^2$（感染的速度快）
• 使用 Push 方式：所有的感染进程，全没有挑选到这个易感进程，推送后依然没被感染，$p_{i+1}=p_i\cdot (1-1/n{)}^{n(1-p_i)}\approx p_i\cdot e^{-1}$（感染的速度慢）

假设每轮，一个感染进程试图去感染 $f$ 个随机进程，那么 $r$ 轮之后，被感染的进程占比约为 $1/(1+n{e}^{-fr})$，因此想要感染全部进程大约需要 ${\log }_{f+1}(n)+\log (n)/f+O(1)$ 轮。也就是说，简单传染病协议最终（eventually）能够感染全部进程。

闲聊（Gossiping）

有 $n$ 个进程，初始化为 inactive 状态（易感）

1. 一个进程成为 active 状态（感染），开始协议
2. 每一个 active 的进程，都随机挑选一个进程传播流言
   1. 如果对方是一个 inactive 的进程，那么使得对方也进入 active 状态
   2. 如果对方是一个 active 或者 removed 的进程，那么自己有 $1/k$ 的概率成为 removed 状态（移除）

假设易感、感染、移除的占比为 $s,i,r$，满足 $s+i+r=1$，易知
$$\begin{array}{rl}\frac{ds}{dt}& =-si\\ \frac{di}{dt}& =si-\frac{(1-s)i}{k}\\ \frac{dr}{ds}& =\frac{1}{ks}-\frac{1+k}{k}\end{array}$$

从而 $i(s)=-\frac{1+k}{k}s+\frac{1}{k}\log s+C$，当 $s=e^{-(k+1)(1-s)}$ 时它为零，因此 $s$ 会随着 $k$ 指数级减小。当 $k=3$ 时 $s\le 0,02$，当 $k=4$ 时 $s\le 0.007$。Gossiping 无法保证（guarantee）所有节点都会更新，但几乎（almost）所有节点都更新了。

P2P 路由

在 peer-to-peer 网络中，需要 P2P Lookup / Routing：

1. 功能需求：节点的加入和退出、资源的定位和交互、存储和查找数据
2. 非功能需求：全局可扩展性、负载平衡、数据安全

基本术语：

• 节点的 nodeID：一个 128 位的 GUID（Globally Unique IDentifiers）
• 对象的 objectID：一个 128 位的 GUID，该对象被存放在最靠近的 nodeID 的服务器上
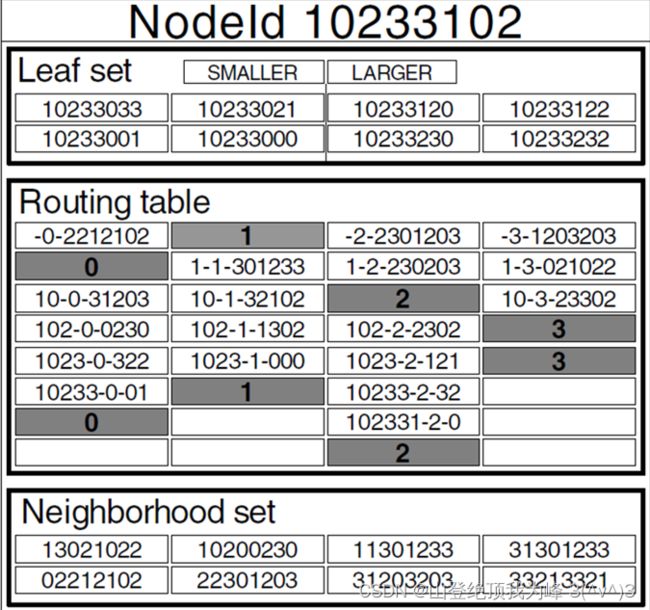
• 叶子集合（leaf set）：大小 $2l$ 的向量，包含与当前节点 nodeID 相邻的（$l$ 个小于、$l$ 个大于）的其他节点的 nodeID 以及 IP
• 邻居集合（neighborhood）：大小 $M$ 的向量，包含 $M$ 个物理上与当前节点最近的其他节点的 nodeID 以及 IP

Circular routing

服务器排成一个圆，仅使用叶子集合的信息，是可以把 objectID 路由到对应的 nodeID 上。

然而，这是十分低效的！

Pastry

Pastry 使用 Prefix Routing 方式，额外再维护一个路由表（Routing table）：有 $32$ 行（GUID 的 $128/4$ 位 $16$ 进制数），每行 $16$ 列（一个 $16$ 进制数的列举 $2^4$）。上图显示了前缀为 $0x65A1\cdots$ 的 nodeID 上所维护的路由表。一般地，路由表不会全部填满，后面的行中大多数是 $null$ 的。

路由算法：消息 $M$，目的节点 $D$，当前节点 $A$，叶子集合 $L$，路由表 $R$，

1. 如果 $L[-l]\le D\le L[l]$，
   1. 把 $M$ 发送到最靠近 $D$ 的节点 $L_i$ 上
   2. 或者发送到当前节点 $A$ 上
2. 否则，使用路由表查找更近节点
   1. 计算 $D$ 和 $A$ 的最长前缀，长度 $p$，令 $i=D[p+1]$ 是下一个不同的数
   2. 如果 $R[p,i]\ne null$，把 $M$ 发送到节点 $R[p,i]$ 上
   3. 否则，在 $R$ 和 $L$ 中找出一个前缀匹配为 $p$ 的节点，它的 GUID 数值上更接近 $D$，将 $M$ 发送给它

在 $N$ 个节点的网络中，可以在 $O(\log N)$ 步将消息路由到任意 GUID 的地址上。

节点加入：

1. 新节点的 GUID 为 $X$，联系物理接近的节点 $A$，发送目标地址为 $X$ 的消息。然后 $A$ 按照上述路由算法转发消息给 $B,C,\cdots$，最终抵达最接近的节点 $Z$
2. $X$ 的路由表：
   1. 由于 $A$ 是 $X$ 的邻居，因此 $A$ 的路由表第 $0$ 行 $A_0$ 可以作为 $X_0，$
   2. 然后 $B$ 与 $X$ 有长为 $1$ 的相同前缀，因此 $B_1$ 可以作为 $X_1$，
   3. 接着从 $C$ 获取 $C_2$ 作为 $X_2$，以此类推。
3. $X$ 的叶子集合：由于 $Z$ 是与 $X$ 最接近的节点，因此 $Z$ 的叶子集合 $L$ 是最理想的近似。
4. 调整：$X$ 将上述得到的路由表和叶子集合，发送给路由表和叶子集合中的所有节点。这些节点调整他们的路由表和叶子节点。

节点失效：

1. 如果发现有其他的某个节点 $D$ 失效了，
2. 修复叶子集合：找到靠近 $D$ 的某个活结点，获取它的叶子集合 $L^{\prime }$，其中有一个 GUID 适合替换 $D$
3. 修复路由表：基于“一旦发现”机制，如果路由失败，那么使用同一行的其他项。采取 Gossip 协议，定期交换路由表信息。

应用层多播

ESM

End System Multicast，用于因特网上视频的实时多播。树结构。

关键问题：如何维护成员信息、如何加入、如何退出（优雅离开、失败）、如何调整结构以获得更高性能。

1. 节点加入：
   1. 询问树根，获得树根维护的节点集合的随机子集
   2. 探测这个节点集合，获取性能（吞吐量、延迟）以及饱和度
   3. 去掉饱和的节点，然后选择一个性能高的节点作为自己的父节点
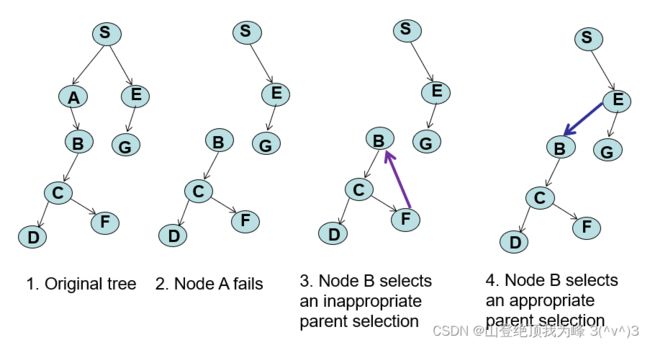
2. 节点退出：
   1. 优雅（gracefully）：通知自己的孩子，并维持一段时间继续转发数据流
   2. 失败（failure）：定期发送 alive 消息给孩子，如果超时则孩子可以发现失败
   3. 孩子们重新选择一个合适的父节点，需要检查，不能是原父节点的后代

Scribe

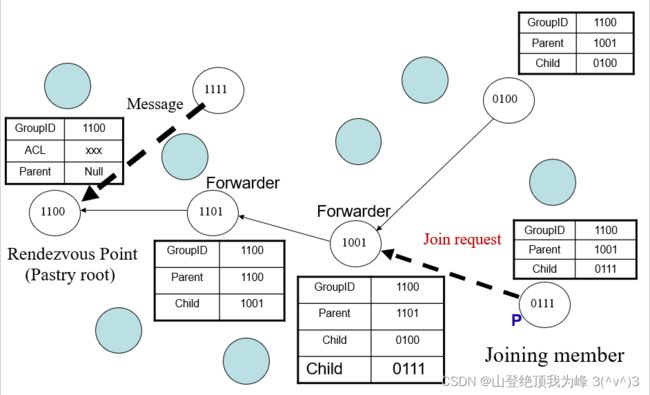
Scribe 建立在 Pastry 之上，每个多播组有自己的 groupID，数值上最接近 groupID 的节点作为汇聚点（rendezvous point）成为树根。树上的其他节点叫做转发点（forwarder）。

1. 创建组：某节点想要创建一个 groupID 的组，使用路由协议发送消息给汇聚点，路径上的每个节点都记录自己的 groupID, Parent, Child
2. 加入组：某节点想要加入 groupID 的组，发送 join request 给某个转发点，维护 Parent, Child 信息
3. 多播：某节点想要对 groupID 发送消息，那么发送给汇聚点 root，然后依次发送给孩子们
4. 离开组：某节点想要离开组，给自己的 parent 发送 leave request
5. 修复树：如果某节点发现 parent 失败了，那么从路由表中选择另一个靠近 groupID 的节点，发送 join requset 给它，让后者加入此多播组

中间件通信协议

Middleware Communication Protocols：

• Remote Procedure Call (RPC)：远程过程调用
• Remote Method Invocation (RMI)：远程方法调用
• Message-Oriented Middleware (MOM)：面向消息的中间件
• Stream-Oriented Communication：面向流的通信

RPC

思想：让调用远端过程，就如同调用本地过程一样（透明性，transparency）

RPC 的执行流程（共 $6$ 个实体——进程、桩、操作系统）：

1. 客户进程调用客户桩（client stub）

2. 客户桩打包（pack）参数，调用本地 OS

3. 客户机 OS 发送消息给远端 OS

4. 服务器 OS 接收消息，传给服务器桩（server stub）

5. 服务器桩解包（unpack）参数，调用服务器进程

---

6. 服务器进程完成，将结果返回给服务器桩

7. 服务器桩打包结果，调用本地 OS

8. 服务器 OS 发送结果给客户机 OS

9. 客户机 OS 接收消息，传给客户桩

10. 客户桩解包结果，返回给客户进程

不过，要注意机器之间传递参数的格式是否一致，例如：编码格式、大小端、引用调用

RPC 语义：

1. At least once semantics：保证至少传递一次
2. At most once semantics：保证至多传递一次
3. Maybe：什么也不能保证
4. Can RPC have the exactly once semantics similar to the local calls? No.

RPC Failures and Solutions：

1. 客户机无法 locate 服务器。使用 exception 机制，把错误转化为异常。
2. 客户发出的 request 消息丢失。在 stub 上设置 timer，超时重发。
3. 服务器接收到请求后 crash 了。客户 stub 设置计时器，
   1. 至少一次语义：超时重发 request，服务器再次执行
   2. 至多一次语义：客户 stub 立刻放弃，并返回一个错误
   3. Maybe 语义：什么也不保证
4. 服务器发送的 reply 消息丢失。客户 stub 设置计时器，
   1. 至少一次语义：超时重发 request，服务器再次执行
   2. 至多一次语义：过滤重复的 request，如果没执行过，那么重新执行；否则，简单重发 reply
5. 客户接收到回应后 crash 了。这个没有什么好的办法，下面的方案也不实用，
   1. Extermination：消灭，客户 stub 记录 log，重启后杀死服务器上的孤儿进程
   2. Reincarnation：转世，客户重启后广播消息，服务器杀死孤儿
   3. Expiration：过期，每条 RPC 都有一个标准时间，如果没能结束就需要显式请求一个新的时间量

因此，解决方案如下图所示

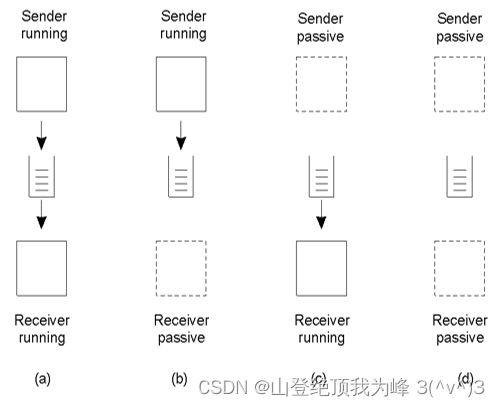
MOM

MOM（消息队列，Message-queuing systems）提供持久的（persistent）异步（asynchronous）通信，并为消息提供存储，不需要发送方与接收方在消息传递过程中处于 active 状态。在发送方发送消息时，不要求接收方进程正在运行；在接收方进程接收消息时，不要求发送方进程也在工作。

多种队列：

• Transient（瞬时） queue, persistent（持久） queue, transactional（事务） queue
• Local queue, remote queue
• Source queue, destination queue

APIs：

1. Put：在队列中 append 消息
2. Get：阻塞，直到队列非空，接着 remove 队首元素
3. Poll：不阻塞。检查指定的队列，remove 队首元素
4. Notify：在特定队列上 install 一个 handler，当新消息到达后调用它

进程协作

多个并发进程要求访问共享资源时，进程在共享资源上需要协调工作，才能不致于发生冲突，且保证共享资源的正确性和完整性。

进程协作的分类：

• 如何保证临界区资源的互斥利用 — 分布式互斥
• 如何从多个并发进程中选举出一个进程扮演协调者 — 选举
• 如何就一组进程间发生的事件的发生顺序达成一致 — 事件排序、排序组播
• 要求一组进程对共享资源进行公平的原子访问，不出现死锁，不出现饿死 — 分布式死锁
• 在异步网络中模拟时钟的滴答(tick, round)—同步器

有序组播

一个组称为是封闭的组，如果只有组的成员可以组播到它。一个组称为是开放的组，如果组外的进程可以发送组播消息给它。重叠组，一个进程属于两个组。用单播实现组播时，同属一组的一些成员从同一个发送者接收的数据包的顺序可能与其他一些成员不一样。

有序组播：

• FIFO排序：
  • 如果一个进程先发出 $multicast(g,m)$，然后发出 $multicast(g,m^{\prime })$
  • 那么，每个传递 $m’$ 的正确进程将在 $m’$ 前传递 $m$
• 因果排序：
  • 如果 $multicast(g,m)\to multicast(g,m^{\prime })$，其中 $\to$ 是发生在先关系且只由 $g$ 的成员之间发送的消息引起
  • 那么，任何传递 $m’$ 的正确的进程将在 $m’$ 前传递 $m$
  • 因果排序隐含 FIFO 排序
• 全排序：
  • 如果一个正确的进程在传递 $m’$ 前传递消息 $m$
  • 那么，任何其它传递 $m’$ 的正确的进程将在 $m’$ 前传递 $m$
  • 全排序未必是 FIFO 或因果排序
• 混合排序：FIFO - 全排序，因果 - 全排序
• 有序组播不提供可靠性：
  • 如果一个正确的进程先发生关于 $m$ 的事件，然后发生关于 $m^{\prime }$ 的事件
  • 那么，另一个传递了 $m$ 的正确进程，可能并不会传递 $m’$ 以及它后面的任意消息

假设：

1. 进程间通信是可靠的，基于 one-to-one 信道
2. 进程只可能因为 crashing 而 fail
3. 对于排序属性，进程一次至多属于一个多播组
4. $multicast(g,m)$：发送消息 $m$ 到组 $g$ 的所有进程
5. $deliver(m)$：传递消息 $m$ 给进程（传递 $\ne$ 接收）
6. 每个消息 $m$ 都有唯一发送者 ID $sender(m)$ 以及唯一目标组 ID $group(m)$

基本组播

Basic Multicast：只要发送者没有 crash，一个正确的进程最终（eventually）会传递消息。

• $B-multicast(g,m)$：对于每个 $p\in g$，分别执行 $send(p,m)$
• $receive(m)$：在 $p$ 上收到 $m$，然后 $B-deliver(m)$

FIFO 组播

进程 $p$ 维护两个变量

1. $S_g^p$：进程 $p$ 发送到组 $g$ 中的消息数
2. $R_g^q$：进程 $p$ 已传递的由进程 $q$ 发送到到组 $g$ 中的顺序数

算法如下：

• $FO-multicast(g,m)$：
  1. 调用 $B-multicast(g,⟨m,S_g^p⟩)$
  2. 设置 $S_g^p=S_g^p+1$
• $B-deliver(m)$：
  1. 收到来自 $q$ 的消息 $⟨m,S⟩$
  2. 如果 $S=R_g^q+1$，那么是预期的消息，于是 $FO-deliver(m)$，接着 $R_g^q:=S$
  3. 如果 $S>R_g^q+1$，那么前面还有消息还没到达，将 $(S,m)$ 放入保留队列，直到 $S=R_g^q+1$ 时再传递它

全排序组播

需要给消息序列指定一个组的顺序数 $S_g$，有两种方案：集中式、分布式。

定序者

一个多播组指定某个进程 $p^{\ast }$ 成为 sequencer，每个进程都持有自己的 $r_g$（预期的顺序数）

组成员，

• $Initialization$：设置 $r_g:=0$
• $TO-multicast(g,m)$：调用 $B-multicast(g\cup p^{\ast },⟨m,i⟩)$
• $B-deliver(⟨m,i⟩)$：把 $(i,m)$ 放入保留队列 $Q$
• $B-deliver(⟨order,i,S⟩)$：
  1. 等到 $(i,m)\in Q$ 并且 $S=r_g$，此时是预期的下一个消息
  2. 执行 $TO-deliver(m)$，然后设置 $r_g:=S+1$

定序者，

• $Initialization$：设置 $S_g:=0$
• $B-deliver(⟨m,i⟩)$
  1. 执行 $B-multicast(g,⟨order,i,S_g⟩)$
  2. 设置 $S_g:=S_g+1$

分布式协商

进程 $p$ 维护两个变量

1. $A_g^p$：进程 $p$ 从组 $g$ 观察到的最大的协定顺序数
2. $P_g^p$：进程 $p$ 提出的最大协定顺序数

算法如下：

• $TO-multicast(g,m)$：
  1. 进程 $p$ 执行 $B-multicast(g,⟨m,i⟩)$，这里 $i$ 是消息的 UID
  2. 等待，收集组 $g$ 的所有提议顺序数，选择其中最大的数 $a$ 作为此消息的顺序数
  3. 执行 $B-multicast(g,⟨order,i,a⟩)$
• $B-deliver(⟨m,i⟩)$
  1. 进程 $p$ 计算 $P_g^p:=\max (A_g^p,P_g^p)+1$
  2. 执行 $B-multicast(g,⟨i,P_g^p⟩)$，提议 $P_g^p$ 作为顺序数
  3. 把 $(P_g^p,m,i)$ 放入保留队列 $Q$
  4. 排序，使得最小顺序数在队首
• $B-deliver(⟨order,i,a⟩)$
  1. 进程 $p$ 设置 $A_g^p:=\max (A_g^p,a)$
  2. 找到 $Q$ 中的项 $(P_g^p,m,i)$，把它修改为 $(a,i,m,tag:=1)$
  3. 如果 $a>P_g^p$ ，那么然后保留队列重新排序（冒泡一个元素）
  4. 等到消息 $m$ 被设置了 $tag=1$ 且位于队首，执行 $TO-deliver(m)$

因果序组播

进程 $p_i,i=1,\cdots ,N$ 维护一个向量 $V_i^g[1\cdots N]$，记录来自进程 $p_j$ 的发生在先的组播消息计数。

• $Initialization$：进程 $p_i$ 设置 $V_i^g[j]=0,\forall j$
• $CO-multicast(g,m)$：
  1. 首先设置 $V_i^g[i]:=V_i^g[i]+1$
  2. 然后执行 $B-multicast(g,⟨m,V_i^g⟩)$
• $B-deliver(⟨m,V_j^g⟩)$
  1. 把 $(m,V_j^g)$ 放入保留队列
  2. 等待，直到 $V_j^g[j]=V_i^g[j]+1$（$p_i$ 已经传递 $p_j$ 先前已发送的组播消息）并且 $V_j^g[k]\le V_i^g[k],\forall k\ne j$（$p_j$ 传递的其他进程 $p_k$ 发送的组播消息，进程 $p_i$ 也同样都已经传递）
  3. 执行 $CO-deliver(m)$，然后设置 $V_i^g[j]:=V_i^g[j]+1$

分布式互斥

目标：实现对进程共享资源的排他性访问，保证访问共享资源的一致性。

具体手段：基于消息传送。

一些术语：

• 进程历史、系统的全局历史、割集、割集的边界、一致的割集、一致的全局状态。
• 走向 (run) 是对全局历史中所有事件的全排序。同时，它与每个本地历史排序是一致的。
• 一致的走向 (consistent run) 或线性化走向 (linearization) 是与全局历史上的发生在先关系一致的所有事件的一个排序。
  • 不是所有的走向都经历一致的全局状态，
  • 所有线性化走向仅经历一致的全局状态。
• 如果有一个（合理的，可以不实际发生）经过状态 $S$ 和 $S’$ 的线性化走向，那么状态 $S’$ 是从状态 $S$ 可达的。

安全性（safety）：设 $\alpha$ 是一个系统全局状态不希望有的性质，该性质是一个系统全局状态的谓词。关于 $\alpha$ 的安全性是一个断言：对所有可从 $S_0$ 到达的所有状态 $S$，$\alpha$ 的值为 False（坏事从不发生，Bad things never happen）。

活性（liveness）：设 $\beta$ 是一个系统全局状态希望有的性质。关于 $\beta$ 的活性是指，对任一从状态 $S_0$ 开始的线性化走向 $L$，对可从 $S_0$ 到达的状态 $S_L$，$\beta$ 的值为 True（好事最终会发生，Good things eventually happen）。

互斥的基本要求：

1. ME1：互斥（mutual exclusion, a safety property），同一时刻至多只有一个进程位于临界区（critical section, CS）内执行
2. ME2：最终（eventually）可以成功进入和离开临界区（freedom from deadlocks and livelocks），
   1. 无死锁：至少有一个进程，必须拥有进入 CS 的资格（a safety property）
   2. 无饥饿：每个试图进入 CS 的进程，必须最终成功（a liveness property）
3. ME3：满足发生在先顺序（$\to$ order），如果一个进程的请求进入 CS 的 request，相较于另一个进程的 request 发生在先，那么进入 CS 的顺序也是如此。
4. Fairness property：没有饥饿，排序公平

互斥算法评价标准：

• 消耗的带宽：与在每个进入临界区和退出临界区操作中发送的消息数成比例
• 客户延迟：在每个进入和退出操作中由进程导致的客户的延迟时间
• 对系统吞吐量的影响，用同步延迟衡量
  • 吞吐量是每秒能处理的对临界区操作的请求个数，吞吐量 = 1 / (同步延迟 + 进程在临界区内工作的最大时间值)
  • 同步延迟：一个进程离开临界区和下一个进程进入临界区之间的时间

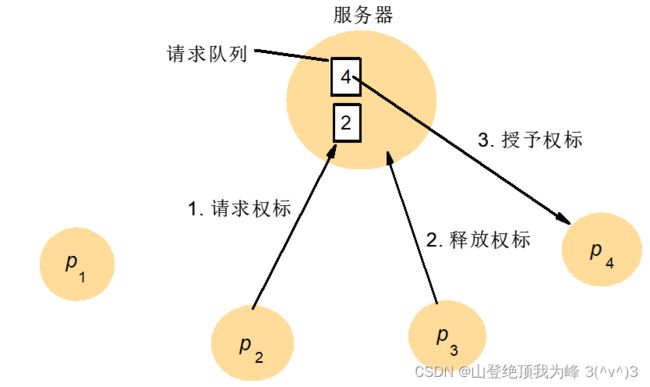
中央服务器互斥算法

A token-based centralized solution：由一个中央服务器，接收各个进程的 request，维护一个请求队列，发放权标（token）

进程：

• 请求权标：试图进入临界区
• 释放权标：离开临界区

服务器：

• 授予权标：有权利进入临界区

性能：

1. 如果系统不发生故障，那么它满足 ME1 和 ME2（安全性条件、活性条件），但是不满足 ME3（顺序条件）。
2. 进入 CS 需要两个消息，客户延迟是系统的往返时间。离开 CS 需要一个消息，没有客户延迟。
3. 从释放消息发出，到授权消息到达，同步延迟是系统的往返时间。
4. 服务器会成为吞吐量的性能瓶颈
5. 服务器会单点失败，需要 backup 节点

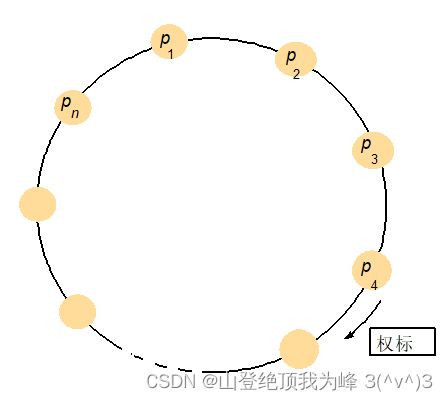
基于环的互斥算法

A token-based distributed solution：把进程安排成一个环，每个进程只有对下一个进程的单向信道。

算法流程：token 在环上单向传递

1. 某个进程想要进入 CS，等待直到获得 token，然后进入 CS
2. 某个进程退出 CS 时，把 token 发送给下一个进程
3. 某个进程不需要进入 CS，直接把 token 传递给下一个进程

性能：

1. 如果系统不发生故障，那么它满足 ME1 和 ME2，但是不满足 ME3。
2. 持续消耗网络带宽
3. 客户延迟：从 $0$ 个到 $N$ 个消息
4. 同步延迟，从 $1$ 个到 $N$ 个消息
5. 故障：进程 crash，丢失 token

Lamport 算法

A permission-based distributed solution。假设消息传递是 FIFO、可靠的、异步的。

时间戳 $(C(e),pid)$，如果 $a\to b$，那么

• 要么 $C(a)<C(b)$
• 要么 $C(a)=C(b)$ 并且 $pid(a)<pid(b)$

每个进程在维护一个 local request queue $Q$，其中的 request 根据时间戳按照“因果-全排序”。

有三种类型的数据：request、reply、release

1. $p_i$ 发送请求 $request(C(re{q}_i),i)$ 给全部进程（包括自己）
2. 当 $p_j$ 接收到 $request(C(re{q}_i),i)$ 后，放入 $Q$，并马上应答 $reply(C(re{p}_j),j)$ 给 $p_i$
3. $p_i$ 可以进入 CS，如果下面的两个条件都成立：
   1. $p_i$ 自己的请求位于 $Q$ 的队首
   2. $p_i$ 已经接收到了全部进程的，满足 $(C(re{q}_i),i)<(C(r_k),k)$ 的某一条消息 $r_k$（可以是三种消息的任何一种）
4. $p_i$ 离开 CS 时，从队首删除自己的请求，并释放 $release(C(re{l}_i),i)$ 给全部进程
5. $p_j$ 接收到了 $release(C(re{l}_i),i)$，从 $Q$ 中删除对应的请求

性能：满足 ME1、ME2、ME3

Ricart-Agrawala 算法

基础算法

这是 Lamport 算法的改进：

• 初始化：
  1. 设置 $state:=RELEASED$
• 进程 $p_i$ 进入 CS：
  1. 设置 $state:=WANTED$
  2. 多播 $multicast(g,(re{q}_i,T))$，其中 $T$ 是本请求的时间戳
  3. 等待，直到收集 $N-1$ 个 $re{p}_j$
  4. 设置 $state:=HELD$
• 进程 $p_j$ 接收到请求：
  1. 如果 $state=HELD$ 或者 $state=WANTED\wedge (T,p_j)<(T_i,p_i)$
  2. 那么，把 $re{q}_i$ 放入队列，不要发送 $re{p}_j$
  3. 否则，立即发送 $re{p}_j$（自己没兴趣，或者有兴趣但自己的请求的时间戳更大）
• 进程 $p_j$ 离开 CS：
  1. 设置 $state:=RELEASED$
  2. 对于队列里的所有 $re{q}_i$，发送 $re{p}_j$ 给对应进程 $p_i$

性能：

1. 满足 ME1、ME2、ME3
2. 一个进程进入 CS，需要 $2(n-1)$ 个消息
3. 同步延迟：一个消息传输时间

改进算法

如果想要连续地进入 CS，可以添加一个状态 $JUST-RELEASED$，降低客户延迟

• 初始化：
  1. 设置 $state:=RELEASED$
• 进程 $p_i$ 进入 CS：
  1. 如果 $state\ne JUST-RELEASED$（需要重新请求许可）
     1. 设置 $state:=WANTED$
     2. 多播 $multicast(g,(re{q}_i,T))$，其中 $T$ 是本请求的时间戳
     3. 等待，直到收集 $N-1$ 个 $re{p}_j$
  2. 否则，直接设置 $state:=HELD$（上次自己离开 CS 后，没有其他进程想要进入 CS）
• 进程 $p_j$ 接收到请求：
  1. 如果 $state=HELD$ 或者 $state=WANTED\wedge (T,p_j)<(T_i,p_i)$
  2. 那么，把 $re{q}_i$ 放入队列，不要发送 $re{p}_j$
  3. 否则，
     1. 立即发送 $re{p}_j$（自己没兴趣，或者有兴趣但自己的请求的时间戳更大）
     2. 如果 $state=JUST-RELEASED$，那么设置 $state:=RELEASED$
• 进程 $p_j$ 离开 CS：
  1. 设置 $state:=JUST-RELEASED$
  2. 如果 $Q$ 非空，那么设置 $state:=RELEASED$（有其他进程按序应在自己之前进入 CS）
  3. 对于队列里的所有 $re{q}_i$，发送 $re{p}_j$ 给对应进程 $p_i$

另外，如果每个进程只投一票，投给了一个进程，就不能继续投给另一个进程，那么只需要收集 $(N+1)/2$ 个 majority 的 $re{p}_j$ 就可以了。

Maekawa 投票算法

共 $N$ 个进程，把每个 $p_i$ 关联到一个选举集合 $V_i$，满足

• $p_i\in V_i$，基本要求
• $V_i\cap V_i\ne \varnothing$，任意两个集合的交集非空
• $|V_i|=K$，任意两个集合的大小相同
• 每个 $p_i$ 被包含在 $M$ 个选举集合中

算法如下：

• 初始化：
  1. 设置 $state:=RELEASED$
  2. 设置 $voted:=FALSE$
• 进程 $p_i$ 试图进入 CS：
  1. 设置 $state:=WANTED$
  2. 多播到选举集合 $multicast(V_i,re{q}_i)$，包括自己
  3. 等待，直到收集 $K$ 个 $re{p}_j$
  4. 设置 $state:=HELD$
• 进程 $p_j$ 收到请求：
  1. 如果 $state=HELD$ 或者 $voted=TRUE$
  2. 那么，把 $re{q}_i$ 放入队列，不要回应
  3. 否则，发送 $re{p}_j$ 给 $p_i$，并设置 $voted:=TRUE$
• 进程 $p_i$ 离开 CS：
  1. 设置 $state:=RELEASED$
  2. 多播到选举集合 $multicast(V_i,releas{e}_i)$
• 进程 $p_j$ 收到释放：
  1. 如果 $Q$ 非空，
     1. remove 队首元素，发送 $re{p}_j$ 给对应的进程 $p_i$
     2. 设置 $voted:=TRUE$
  2. 否则，设置 $voted:=FALSE$

最优解：可以达到互斥效果的最小的 $K$

1. 将 $N$ 个进程排列成 $\sqrt{N}\times \sqrt{N}$ 的矩阵，然后进程 $p_i$ 所在的同一列、同一行的那些进程就是 $V_i$
2. 因此 $M=K=2\sqrt{N}-1$

如果进程数不是平方数，那么就比较麻烦了。用 $(N,N,M,K,\lambda )-BIBD$ 可以么？它不一定存在啊！哦，似乎选举集的要求比 BIBD 弱的多。在 $N$ 个进程的情况下，只需要在剩余类 ${\mathbb{Z}}_N$ 中找出一个序列 $A=\{a_1,\cdots ,a_s\}$，使得：对于任意的 $1\le d\le N-1$，都存在 $a_i,a_j\in A$，满足 $a_i-a_j\equiv d(\mathrm{mod}N)$

自己想了一种方法：依次向左右方向跨越 $2^i$ 的距离，$0,1,-2,5,-10,\cdots$。如果含 $k$ 个点，那么它可以支持 $2^k$-1 以内的进程分组。

这个选举集的选择方法是正确的吗？如果有 $N$ 个进程需要分组，那么就计算 $k=\lceil \log (N+1)\rceil$（咦？这比 $\sqrt{N}$ 小得多），然后得到 $\{0,1,-2,\cdots ,(-1{)}^{k-1}\cdot {\sum }_{i=k-1,k-3,\cdots }{2}^i\}$，把这个序列循环移位 $a+1(\mathrm{mod}N)$ 就可以得到 $N$ 个选举集了。例如，$N=13$，那么 $k=4$，计算出 $\{-2,0,1,5\}$，等价于 $\{0,1,5,11\}(\mathrm{mod}13)$，这是第 $pid=0$ 个进程的选举集，然后 $\{1,2,6,12\}$ 就是第 $pid=1$ 个进程的选举集，以此类推。

Emmmm，这个算法似乎不对。对于不同的模数 $N$，不一定能够组装出 $1,\cdots ,N-1$ 的距离 ╮(╯﹏╰）╭

性能：

• 满足 ME1，不满足 ME2（容易死锁）
• 但是如果进程按照发生在先的顺序对队列排序，那么满足 ME2 和 ME3
• 进入 CS 需要 $2\sqrt{N}$ 个消息，退出 CS 需要 $\sqrt{N}$ 个消息
• 同步延迟：系统的往返时间

选举算法

目标：选举算法是所有进程都同意某个进程来扮演特定角色的过程。不失一般性，我们要求选择具有最大标识符的进程为当选进程。

选举的基本要求：

• 假设每个进程 $p_i,i=1,\cdots ,N$ 有一个变量 $electe{d}_i$，用于记录当选进程的标识符。
• E1 (安全性)：所有参与的进程 $p_i$，或者设置 $electe{d}_i=\perp$，或者设置 $electe{d}_i=P$ 是在运行结束时具有最大标识符的非崩溃进程。
• E2 (活性)：所有进程 $p_i$ 都参加选举，并且最终设置 $electe{d}_i\ne \perp$，或者崩溃。

选举算法评价标准：

1. 总的网络带宽的使用
2. 算法的回转时间（turnaround time）：从启动算法到终止算法之间的串行消息传输的次数

基于环的选举算法

假设：

• 系统是异步的，并且系统不发生故障
• 一组进程排列在一个环上，消息沿着环单向传递
• 最小先验知识：每个进程仅知道邻居

选举出具有最大标识符的进程成为协调者，算法如下：

• 初始化：每个进程被标记为非参与者
• 开始选举：
  1. 从任何一个进程 $p_i$ 开始，它标记自己成为参与者
  2. 然后把自己的标识符放入选举消息，传递给下一个进程
• 收到选举消息：比较标识符大小
  1. 如果到达的标识符更大，那么传递给下一个进程
  2. 如果到达的标识符更小，
     1. 若自己不是参与者，那么自己成为参与者，并把标识符替换成自己的，传递给下一个进程
     2. 若自己已经是参与者了，那么不转发消息
  3. 如果到达的标识符是自己的（说明环上自己的标识符最大）
     1. 把自己变成非参与者
     2. 自己成为协调者，然后发送当选信息（包含自己的标识符）给邻居
• 收到当选消息：
  1. 把自己变成非参与者
  2. 设置 $electe{d}_i$ 为消息中的标识符
  3. 如果自己不是协调者，那么就转发当选消息

性能：

1. 满足 E1、E2
2. 最坏情况下，需要发送 $3N-1$ 个消息

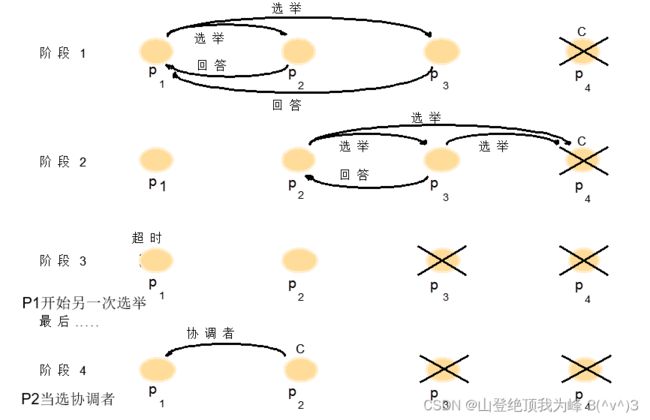
Bully 算法

霸道算法，假设：

• 进程可能崩溃；消息传递是可靠的，并能在一段时间内完成；所有进程知道其他所有进程的标识符 (pid)。
• 系统是同步的，并允许在选举期间进程崩溃。可以构造一个可靠的故障检测器来检测进程故障。

一个进程通过超时机制，发现系统故障，开始一次选举：

• 开始选举：
  1. 发送选举消息给所有更高标识符的进程
  2. 等待回答消息，时间长度 $T$，
  3. 如果超时，就认为自己是协调者，发送协调者消息给更低标识符的进程
  4. 否则，继续等待协调者消息，时间长度 $T^{\prime }$
  5. 如果超时，那么重新开启一次选举
• 收到选举消息：
  1. 发送一个回答消息
  2. 然后自己也开启一次选举（除非已经开始了选举）
• 收到协调者消息：
  1. 设置 $electe{d}_i$ 为消息中的标识符
• 如果已知自己拥有最高标识符，那么直接发送（任何时间，比如从 crash 中恢复）协调者消息给所有其他进程。霸道。

性能：

1. 如果进程崩溃后重启，那么满足安全性条件 E1
2. 如果崩溃的进程被替换成相同标识符的进程，不能保证满足 E1
3. 如果超时值是不准确的（或者说故障检测器是不可靠的），那么不能保证满足 E1
4. 满足活性条件 E2
5. 最好情况需要 $N-2$ 个消息，最坏情况需要 $O(N^2)$ 个消息

Flooding

任意网络上的选举，可以采用洪泛方式，按轮（in rounds）执行

• 初始化：
  1. 任意的进程 $p_i$，设置 leader $L(i):=i$
• 每一轮：
  1. 每个节点发送 $L(i)$ 给自己的所有邻居
  2. 收集邻居发送过来的 pid 到集合 $S_i$ 里
  3. 设置 $L(i):=\max (L(i)\cup S_i)$
• 终止：如果 网络拓扑图的直径是 $D$，那么执行 $D$ 轮后终止算法。

MANET

这个算法比 Flooding 算法更高效。它采用树结构，先向下广播，再向上汇聚：

1. 源节点（source node）开始一次选举，发送选举消息给邻居
2. 节点第一次收到选举消息时，把对方作为自己的 parent，然后转发选举消息给其他所有邻居（作为自己的孩子）
3. 节点再次收到不是来自 parent 的选举消息时，发送一个确认消息 ack，携带上自己的性能数据
4. 节点等到收到所有孩子的 ack 后，才发送 ack 给自己的 parent（如果没有孩子，就直接发送 ack）
5. 最后，源节点将会收到网络上所有节点的性能数据，从中挑选一个最好的节点作为协调者