Day_51-53kNN分类器
目录
Day_51:kNN分类器
一. 前言
二. 机器学习基本术语
三. kNN算法的原理
1. kNN算法的思想
2. kNN算法的具体实现过程
四. 代码实现
1. 导包
2. 参数初始化
3. 数据的导入
4. 数据的抽取
5. 对于测试集进行预测
6. 核心代码
Day_52:knn分类器(续)
一. 前言
二. 对于选取k个最近距离的优化
Day_53:kNN 分类器 (续)
一. 增加 weightedVoting() 方法,
二. 实现leave-one-out测试
Day_51:kNN分类器
一. 前言
从这里开始就算正式开始研究生的学习阶段了,前五十天所写的东西大部分是我们本科期间学习过的,但是从这里开始的东西都是关于机器学习的,也是我本科期间没有接触过的理论。加之我本科学的是数学,计算机的东西接触的并不算很多,对于机器学习更是只有简单的概念性的了解,学习的过程中难免会有错误,而且对于这部分的知识我我并不确定能够自己掌握多少,尽力而为。总之一个原则:尽自己最大的能力尽可能写好这一阶段的博客,在这期间如果有问题欢迎指出。
二. 机器学习基本术语
这里写的东西主要是关于机器学习的基本定义,重要定理的注释啥的(从零开始)。
机器学习:机器学习是让计算机像人类一样学习和行动的科学,通过以观察和现实世界互动的形式向他们提供数据和信息,以自主的方式改善他们的学习。机器学习的本质就是针对输入数据(训练集,测试集),计算机帮忙构建函数映射(数学模型),使得这里构建的模型满足你输入的数据(训练集(构建函数映射),测试集(用于测试模型的结果)),最终得到的函数映射的这个过程。
监督学习:从已知类别的数据集中学习出一个函数,这个函数可以对新的数据集进行预测或分类,数据集包括特征值和目标值,即有标准答案;常见算法类型可以分为:分类和回归。
无监督学习:与监督学习的主要区别是,数据集中没有人为标注的目标值,即没有标准答案;常见算法有:聚类,生成对抗网络。
半监督学习:是监督学习与无监督学习相结合的一种学习方法。半监督学习使用大量的未标记数据,以及同时使用标记数据,来进行模式识别工作。例如,在图像分类任务中,真实标签由人类标注者给出的。从互联网上获取巨量图片很容易,然而考虑到标记的人工成本,只有一个小子集的图像能够被标注,其他样本无法拥有标签。
训练集:其实本质上就是输入的第一部分,首先输入数据,接着对于输入数据进行处理,构建出的函数;这部分输入的数据被称为训练集。
验证集:输入第二部分数据,这部分数据就是用来验证我们得到的函数能否处理这些数据,若能处理,则验证成功;若不能处理,则验证失败。
测试集:这部分其实和验证集容易搞混,这里其实相当于我背着“答案”去寻找答案;比如我构建模型完成,输入了几张图片(我知道这个图片的结果),然后用我们刚刚构建的模型(函数)计算得到结果,将真实的结果和计算出来的结果比对,这部分数据就是测试集。
这里举一个十分形象的例子:
- 训练集-----------学生的课本;学生根据课本里的内容来掌握知识。
- 验证集-----------作业;通过作业可以知道不同学生学习情况、进步的速度快慢。
- 测试集-----------考试;考的题是平常都没有见过,考察学生举一反三的能力。
三. kNN算法的原理
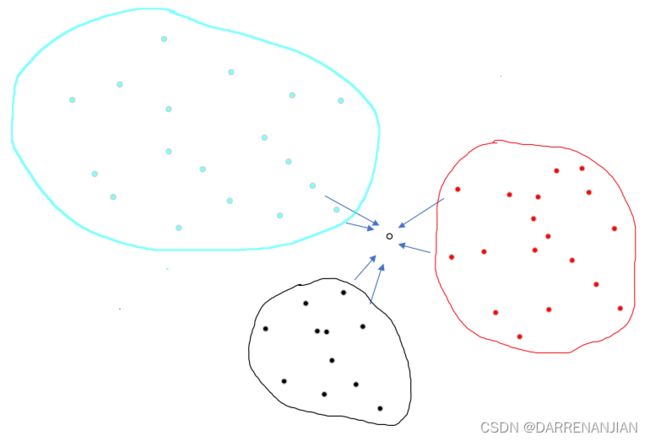
1. kNN算法的思想
kNN算法的思想非常简单:第一部分训练接:输入任意组n维向量;接着输入一个n维向量向量,对应于特征空间中的一个点,输出结果为该特征向量所对应的类别标签或预测值。即首先输入大量的数据(这些数据都是有类名的),然后输入一个没有类名的数据,我们根据前面输入的大量数据判断这个没有类名的数据应该归为哪一类,这就是kNN算法的思想。
2. kNN算法的具体实现过程
那么我们需要怎么判断?首先kNN算法没有学习的过程,被称为惰性学习,类似于开卷考试,,在已有数据中去找答案。
①首先我们计算出训练集的每个样本到这个需要我们判断类别的样本的“距离”,这里的距离一般有以下这么几种:
欧氏距离:![]()
曼哈顿距离:![]()
闵可夫斯基距离![]()
注:对于闵可夫斯基距离,当p=1时为曼哈顿距离,p=2时为欧氏距离,在这里我们取距离的度量为欧氏距离。
②我们确定k值,k代表的是测试样本选取周围临近的邻居的个数(一般事先指定小于20,是一个确定值)
③分类决策规则:就是说我们根据何种方式来确定测试样本的归类,举个例子:我们选用欧氏距离来度量距离,选定k为7,选定分类决策规则为根据就近k个训练样本类别的数量多少来判断,这k个样本最终哪个类多,那么这个测试样本就归属于哪一个类。
四. 代码实现
其实kNN算法的思想和实现过程都很简单,就是根据最近的点是什么类,就来判断测试样本是什么类,主要难在代码实现上。
1. 导包
这里我们需要首先导入一个数据处理包weka,下载地址:https://mvnrepository.com/
将数据处理包导入IntelliJ IDEA 的详细过程:网址
只有完成这两部,我们才可以使用Instances类(关于数据处理的类)
import weka.core.Instances;
import java.io.FileReader;
import java.util.Arrays;
import java.util.Random;
//--构建数据处理的对象
Instances dataset;除此之外,我们还需要导入数据;详细的数据包的下载地址:网址
下载完成后保存到电脑的路径:D:/data
保存名字及格式为iris.arff
2. 参数初始化
用MANHATTAN表示曼哈顿计算方法,EUCLIDEAN表示欧拉计算方法,distanceMeasure表示这个系统采用的什么算法(欧拉还是曼哈段,最终我们取欧拉距离作为评判标准),构造了一个随机数类用于后面打乱数据,设置邻居个数为7,设置数据对象dataset用于存储数据集,设置训练集的对象trainingSet,设置测试集的对象testingSet,设置测试集的预测结果predictions
/**
* Manhattan distance.
*/
public static final int MANHATTAN = 0;
/**
* Euclidean distance.
*/
public static final int EUCLIDEAN = 1;
/**
* The distance measure.
*/
public int distanceMeasure = EUCLIDEAN;
/**
* A random instance;
*/
public static final Random random = new Random();
/**
* The number of neighbors.
*/
int numNeighbors = 7;
/**
* The whole dataset.
*/
Instances dataset;
/**
* The training set. Represented by the indices of the data.
*/
int[] trainingSet;
/**
* The testing set. Represented by the indices of the data.
*/
int[] testingSet;
/**
* The predictions.
*/
int[] predictions;
/**
* ********************
* The first constructor.
*
* @param paraFilename The arff filename.
* ********************
*/3. 数据的导入
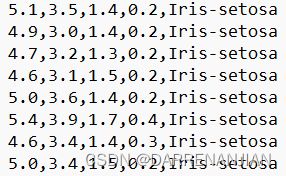
由于导包的数据为以下格式,前四列表示这个东西的参数,最后一列表示它的属性。
将数据从数据包导入,设置属性值为4类。
/**
* ********************
* The first constructor.
*
* @param paraFilename The arff filename.
* ********************
*/
public KnnClassification(String paraFilename) {
try {
FileReader fileReader = new FileReader(paraFilename);
dataset = new Instances(fileReader);
// The last attribute is the decision class.
dataset.setClassIndex(dataset.numAttributes() - 1);
fileReader.close();
} catch (Exception ee) {
System.out.println("Error occurred while trying to read \'" + paraFilename
+ "\' in KnnClassification constructor.\r\n" + ee);
System.exit(0);
} // Of try
}// Of the first constructor4. 数据的抽取
首先构建一个存储数据的数组tempIndices[ ]用来存放打乱数据点索引,接着用trainingSet存储前0.8份,testingSet存储后0.2份(因为这里我们按0.8 是训练集,0.2是测试集)
抽取数据的代码如下:
/**
* ********************
* Split the data into training and testing parts.
*
* @param paraTrainingFraction The fraction of the training set.
* ********************
*/
public void splitTrainingTesting(double paraTrainingFraction) {
int tempSize = dataset.numInstances();
int[] tempIndices = getRandomIndices(tempSize);
int tempTrainingSize = (int) (tempSize * paraTrainingFraction);
trainingSet = new int[tempTrainingSize];
testingSet = new int[tempSize - tempTrainingSize];
for (int i = 0; i < tempTrainingSize; i++) {
trainingSet[i] = tempIndices[i];
} // Of for i
for (int i = 0; i < tempSize - tempTrainingSize; i++) {
testingSet[i] = tempIndices[tempTrainingSize + i];
} // Of for i
}// Of splitTrainingTesting构建大小为paraLength的数组,每个数组里面存放随机的数字,这些数字的范围为0-paraLength的不重复的数字。
/**
* ********************
* Get a random indices for data randomization.
*
* @param paraLength The length of the sequence.
* @return An array of indices, e.g., {4, 3, 1, 5, 0, 2} with length 6.
* ********************
*/
public static int[] getRandomIndices(int paraLength) {
int[] resultIndices = new int[paraLength];
// Step 1. Initialize.
for (int i = 0; i < paraLength; i++) {
resultIndices[i] = i;
} // Of for i
// Step 2. Randomly swap.
int tempFirst, tempSecond, tempValue;
for (int i = 0; i < paraLength; i++) {
// Generate two random indices.
tempFirst = random.nextInt(paraLength);
tempSecond = random.nextInt(paraLength);
// Swap.
tempValue = resultIndices[tempFirst];
resultIndices[tempFirst] = resultIndices[tempSecond];
resultIndices[tempSecond] = tempValue;
} // Of for i
return resultIndices;
}// Of getRandomIndices5. 对于测试集进行预测
这重载了predict函数,第一个predict函数是构建测试集的预测结果的容器predictions,接着对每个测试集进行预测predictions[i] = predict(testingSet[i]);
第二个predict函数用computeNearests函数计算出这个测试样本的最近的k个邻居的编号,再用simpleVoting函数选出这个测试样本的类,返回类名。
/**
* ********************
* Predict for the whole testing set. The results are stored in predictions.
* #see predictions.
* ********************
*/
public void predict() {
predictions = new int[testingSet.length];
for (int i = 0; i < predictions.length; i++) {
predictions[i] = predict(testingSet[i]);
} // Of for i
}// Of predict
/**
* ********************
* Predict for given instance.
*
* @return The prediction.
* ********************
*/
public int predict(int paraIndex) {
int[] tempNeighbors = computeNearests(paraIndex);
int resultPrediction = simpleVoting(tempNeighbors);
return resultPrediction;
}// Of predict6. 核心代码
6.1计算最近的k个邻居的编号
具体的计算过程如下:计算每个训练样本与某一个测试样本的距离,将他们的值放入对应的距离数组tempDistances,在计算完成的的距离里面寻找到最近的k个点,然后返回这k个点的坐标。
/**
* ***********************************
* Compute the nearest k neighbors. Select one neighbor in each scan. In
* fact we can scan only once. You may implement it by yourself.
*
* @param paraK the k value for kNN.
* @param paraCurrent current instance. We are comparing it with all others.
* @return the indices of the nearest instances.
* ***********************************
*/
public int[] computeNearests(int paraCurrent) {
int[] resultNearests = new int[numNeighbors];//返回最近的邻居的编号
boolean[] tempSelected = new boolean[trainingSet.length];//?
double tempMinimalDistance;//临时距离的最小值
int tempMinimalIndex = 0;//临时距离对应的节点
// Compute all distances to avoid redundant computation.
double[] tempDistances = new double[trainingSet.length];//记录每个训练集样本到paraCurrent点的距离
for (int i = 0; i < trainingSet.length; i++) {
tempDistances[i] = distance(paraCurrent, trainingSet[i]);
}//Of for i
// Select the nearest paraK indices.
for (int i = 0; i < numNeighbors; i++) {
tempMinimalDistance = Double.MAX_VALUE;
for (int j = 0; j < trainingSet.length; j++) {
if (tempSelected[j]) {
continue;
} // Of if
if (tempDistances[j] < tempMinimalDistance) {
tempMinimalDistance = tempDistances[j];
tempMinimalIndex = j;
} // Of if
} // Of for j
resultNearests[i] = trainingSet[tempMinimalIndex];
tempSelected[tempMinimalIndex] = true;
} // Of for i
System.out.println("The nearest of " + paraCurrent + " are: " + Arrays.toString(resultNearests));
return resultNearests;
}// Of computeNearests
6.2计算距离
这里有有两种计算方式,只取欧式距离的计算。
/**
* ********************
* The distance between two instances.
*
* @param paraI The index of the first instance.
* @param paraJ The index of the second instance.
* @return The distance.
* ********************
*/
public double distance(int paraI, int paraJ) {
double resultDistance = 0;
double tempDifference;
switch (distanceMeasure) {
case MANHATTAN:
for (int i = 0; i < dataset.numAttributes() - 1; i++) {
tempDifference = dataset.instance(paraI).value(i) - dataset.instance(paraJ).value(i);
if (tempDifference < 0) {
resultDistance -= tempDifference;
} else {
resultDistance += tempDifference;
} // Of if
} // Of for i
break;
case EUCLIDEAN:
for (int i = 0; i < dataset.numAttributes() - 1; i++) {
tempDifference = dataset.instance(paraI).value(i) - dataset.instance(paraJ).value(i);
resultDistance += tempDifference * tempDifference;
} // Of for i
break;
default:
System.out.println("Unsupported distance measure: " + distanceMeasure);
}// Of switch
return resultDistance;
}// Of distance6.3投票分出类别
根据computeNearests返回的数组,可以判断出这几个数据在训练集中是哪几个类,选择类的数量最多的作为这个测试样本的最终结果。
/**
* ***********************************
* Voting using the instances.
*
* @param paraNeighbors The indices of the neighbors.
* @return The predicted label.
* ***********************************
*/
public int simpleVoting(int[] paraNeighbors) {
int[] tempVotes = new int[dataset.numClasses()];
for (int i = 0; i < paraNeighbors.length; i++) {
tempVotes[(int) dataset.instance(paraNeighbors[i]).classValue()]++;
} // Of for i
int tempMaximalVotingIndex = 0;
int tempMaximalVoting = 0;
for (int i = 0; i < dataset.numClasses(); i++) {
if (tempVotes[i] > tempMaximalVoting) {
tempMaximalVoting = tempVotes[i];
tempMaximalVotingIndex = i;
} // Of if
} // Of for i
return tempMaximalVotingIndex;
}// Of simpleVoting6.4数据检验
对于0.2份的测试样本,我们确实是已经知道答案的,然后根据这个knn算法得到的结果和真实的结果比对,若不相等,则tempCorrect自加1,直到0.2份测试样本数据循环结束,用tempCorrect除以这0.2份样本的最终数量,得到精准度。
/**
* ********************
* Get the accuracy of the classifier.
*
* @return The accuracy.
* ********************
*/
public double getAccuracy() {
// A double divides an int gets another double.
double tempCorrect = 0;
for (int i = 0; i < predictions.length; i++) {
if (predictions[i] == dataset.instance(testingSet[i]).classValue()) {
tempCorrect++;
} // Of if
} // Of for i
return tempCorrect / testingSet.length;
}// Of getAccuracyDay_52:knn分类器(续)
一. 前言
这部分的主要是对上面的代码进行优化,我们知道对于测试集假设有m个,对于训练样本集假设有n个,需要进行判断的邻居有k个,那么现在我们上面代码的时间复杂度为:
m(对于m个测试样本进行判断)×(n(每选取一个测试样本就要计算距离)+n×k(要从n个距离里面找k个最小的))
所以上面的时间复杂度为O(m(n+n×k))→O(kmn)
二. 对于选取k个最近距离的优化
这是要求:重新实现 computeNearests,仅需要扫描一遍训练集,即可获得 k 个邻居。提示用插入排序。闵老师的意思就是只用扫描一边训练集(即在计算某一个测试样本到各个训练样本距离的时候,直接选取出最小的k个训练样本)
具体操作如下:这里采用插入排序的思想构建一个k大小的数组,每一次若有距离处在这个数组里面,则更新数组。这里其实就是运用了插入排序,只不过将n个的插入排序替换成了k个的插入排序。
但是优化就结束了吗? 这里我们设计的的确是少了一次的扫描,但是再看看时间复杂度依然是O(kmn),所以这里的优化其实仅仅是少了一次的扫描并没有达到对computeNearests优化的目的,但是这里却给我们提供了一个思路,我们能否将得到的n个距离排序呢?(尽可能减少排序的时间复杂度,这里可以参考张星移师兄的博客,他采用的是堆优化,其实也就是堆排序,不过仅仅取k个最小的数据就行),这里我们可以同样采用另外一种排序算法——快速排序,当然我觉得最好的优化方法还是张星移师兄的堆排序,时间复杂度太低了!这里我们用快速排序得到的时间复杂度为O(mnlogn),当然只有在k大于logn的时候才是优化,即n>2^k。这里只是提供一个思路,其实我不是很建议采用这种方式,因为k实在是太小了!!!k的取值一般为小于20的值,而训练集模糊不定可能很大,可能很小,虽然这里是2^k为指数函数,但是我依然不是很建议这样优化(当k取是10的时候,采用这种优化的话需要训练集>1024,这样有时候反而没有达到优化,只有极端情况,k特别小,训练集n特别大的时候这种方式才有效)。
这里我就补充一下插入排序(扫描一次得到结果),重新实现 computeNearests, 仅需要扫描一遍训练集, 即可获得k个邻居。
/**
* ***********************************
* Compute the nearest k neighbors. Select one neighbor in each scan. In
* fact we can scan only once. You may implement it by yourself.
*
// * @param paranumNeighbors the k value for kNN.
* @param paraCurrent current instance. We are comparing it with all others.
* @return the indices of the nearest instances.
* ***********************************
*/
public int[] computeNearests(int paraCurrent) {
int[] resultNearests = new int[numNeighbors];//返回最近的邻居
double[] tempDistances = new double[trainingSet.length];//记录每个训练集样本到paraCurrent点的距离
resultNearests[0]=0;
tempDistances[0]=distance(paraCurrent, trainingSet[0]);
int k=0,j;
for (int i = 1; i < trainingSet.length; i++) {
tempDistances[i] = distance(paraCurrent, trainingSet[i]);
if(k!=numNeighbors-1){
for(j=k ; tempDistances[resultNearests[j]]>tempDistances[i] ;){
resultNearests[j+1]=resultNearests[j];
j--;
if(j<0)break;
}
resultNearests[j+1]=i;
k++;
}
else {
if(tempDistances[resultNearests[k]]>tempDistances[i]){
for(j=k ; tempDistances[resultNearests[j-1]]>tempDistances[i] ;){
resultNearests[j]=resultNearests[j-1];
j--;
if(j==0)break;
}
resultNearests[j]=i;
}
}
}//Of for i
int[] result = new int[numNeighbors];
for(int i=0;i设置测量距离的方法:setDistanceMeasure()
public void setDistanceMeasure(int paradistanceMeasure) {
if (paradistanceMeasure == 0 || paradistanceMeasure == 1) {
distanceMeasure = paradistanceMeasure;
} else {
System.out.println("设置距离计算方法失败,现在的距离的计算方法仍为"+distanceMeasure);
}
}设置邻居的个数:setNumNeighors() 方法
public void setNumNeighors(int paranumNeighbors){
numNeighbors=paranumNeighbors;
}Day_53:kNN 分类器 (续)
一. 增加 weightedVoting() 方法,
距离越短话语权越大,支持两种以上的加权方式。这里我用了得到的numNeighbors的邻居的距离d,距离的倒数即1/d,这几个邻居的分别属于哪几个类别,将他们距离的倒数分别加到对应的类别里面,最后看这几个类别谁得到的参数大就选谁为这个测试样本的类别。
当然其实这里不以最终得到的邻居结果,而是以所有的训练集样本来计算也可以,距离越短,话语权越大,距离越远,话语权越小。
weightedVoting和simpleVoting是两种不同的投票方式,选一种即可。
public int weightedVoting(int[] paraNeighbors,int paraIndex){
double tempquanzhi ;
double[] votingresult =new double[dataset.numClasses()];
for (int i = 0; i < paraNeighbors.length; i++) {
tempquanzhi= 1.0/distance(paraNeighbors[i],paraIndex);
votingresult[(int) dataset.instance(paraNeighbors[i]).classValue()]+=tempquanzhi;
}
int tempMaximalVotingIndex = 0;
double tempMaximalVoting = 0;
for (int i = 0; i < dataset.numClasses(); i++) {
if (votingresult[i] > tempMaximalVoting) {
tempMaximalVoting = votingresult[i];
tempMaximalVotingIndex = i;
} // Of if
} // Of for i
return tempMaximalVotingIndex;
}二. 实现leave-one-out测试
所谓leave-one-out测试,即将所有数据选作为训练集,选一个样本作为测试集。
这里只需要对splitTrainingTesting函数改写即可。
/**
* ********************
* Split the data into training and testing parts.
*
* @param paraTrainingFraction The fraction of the training set.
* ********************
*/
public void splitTrainingTesting() {
int tempSize = dataset.numInstances();
int[] tempIndices = getRandomIndices(tempSize);
int tempTrainingSize=tempSize-1;
trainingSet=new int[tempTrainingSize];
testingSet=new int[tempSize - tempTrainingSize];
for (int i = 0; i < tempTrainingSize; i++) {
trainingSet[i] = tempIndices[i];
} // Of for i
testingSet[0]=tempIndices[tempTrainingSize];
}leave-one-out测试结果如下(我只进行了10次计算)