简要介绍 | 点云距离度量:从原理到应用
注1:本文系“简要介绍”系列之一,仅从概念上对点云距离度量进行非常简要的介绍,不适合用于深入和详细的了解。
点云距离度量:从原理到应用
3D deep learning on Point cloud
1. 背景介绍
点云数据在计算机图形学、计算机视觉、自动驾驶等领域中具有广泛应用。为了在这些应用中有效地处理和分析点云数据,我们需要衡量点云之间的相似性。这就引出了点云之间的距离度量问题。本文将介绍点云距离度量的基本概念、原理、研究现状和挑战,并探讨未来的发展方向。
2. 原理介绍和推导
点云是由三维空间中的一组离散点组成的,每个点具有X、Y和Z坐标。度量两个点云之间的距离通常包括以下几种方法:
2.1 欧氏距离
欧氏距离(Euclidean distance)是最常用的距离度量方法。对于两个点云 P = { p 1 , p 2 , . . . , p n } P=\{p_1, p_2, ..., p_n\} P={p1,p2,...,pn}和 Q = { q 1 , q 2 , . . . , q n } Q=\{q_1, q_2, ..., q_n\} Q={q1,q2,...,qn},它们之间的欧氏距离定义为:
d ( P , Q ) = ∑ i = 1 n ( p i − q i ) 2 d(P, Q) = \sqrt{\sum_{i=1}^n (p_i - q_i)^2} d(P,Q)=i=1∑n(pi−qi)2
2.2 Hausdorff 距离
Hausdorff距离(Hausdorff distance)是一种用于度量两个点集之间的距离的方法,它可以处理点云之间的非一一对应关系。对于两个点云 P P P和 Q Q Q,它们之间的Hausdorff距离定义为:
d H ( P , Q ) = max { max p ∈ P min q ∈ Q ∥ p − q ∥ , max q ∈ Q min p ∈ P ∥ p − q ∥ } d_H(P, Q) = \max\{\max_{p \in P} \min_{q \in Q} \|p - q\|, \max_{q \in Q} \min_{p \in P} \|p - q\|\} dH(P,Q)=max{p∈Pmaxq∈Qmin∥p−q∥,q∈Qmaxp∈Pmin∥p−q∥}
2.3 Chamfer 距离
Chamfer距离(Chamfer distance)是一种近似Hausdorff距离的方法,计算复杂度更低。对于两个点云 P P P和 Q Q Q,它们之间的Chamfer距离定义为:
d C ( P , Q ) = ∑ p ∈ P min q ∈ Q ∥ p − q ∥ 2 + ∑ q ∈ Q min p ∈ P ∥ p − q ∥ 2 d_C(P, Q) = \sum_{p \in P} \min_{q \in Q} \|p - q\|^2 + \sum_{q \in Q} \min_{p \in P} \|p - q\|^2 dC(P,Q)=p∈P∑q∈Qmin∥p−q∥2+q∈Q∑p∈Pmin∥p−q∥2
3. 研究现状
近年来,点云距离度量在许多领域得到了广泛关注和应用,包括点云配准、点云分类和点云生成等。在这些应用中,研究者们提出了许多改进的距离度量方法,以提高计算效率和应用性能。
3.1 改进的Hausdorff距离
因为Hausdorff距离对噪声和离群点非常敏感,研究者们提出了很多改进的方法。例如,部分Hausdorff距离(Partial Hausdorff distance)通过忽略最远的一部分点对来降低噪声的影响。
3.2 深度学习方法
随着深度学习的发展,一些研究者开始利用神经网络来学习点云之间的距离度量。例如,PointNet和Dynamic Graph CNN等网络结构可以直接处理点云数据,从而学习到更为高级和有意义的特征表示。
4. 挑战
尽管点云距离度量在很多方面取得了显著的进展,但仍然存在一些挑战,例如:
-
计算复杂度:一些距离度量方法(如Hausdorff距离)在大规模点云数据中计算复杂度较高,需要更高效的算法和技术来解决。
-
鲁棒性:现有的距离度量方法对噪声、离群点和遮挡等问题的鲁棒性有待提高。
-
应用性能:在实际应用中,需要根据不同的任务和场景选择合适的距离度量方法,以提高应用性能。
5. 未来展望
未来,点云距离度量的研究和应用将继续深入发展。可能的方向包括:
-
新的距离度量方法:研究更加适合实际应用需求的距离度量方法。
-
算法优化:提高现有距离度量方法在计算效率、精度和鲁棒性等方面的性能。
-
深度学习方法:利用深度学习技术对点云距离度量进行改进和优化,提高应用性能。
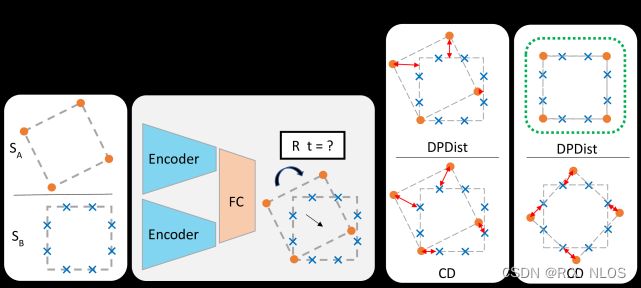
DPDist : Comparing Point Clouds Using Deep Point Cloud Distance
6. 代码示例
以下是一个使用Python和NumPy库计算两个点云之间欧氏距离的简单示例:
import numpy as np
def euclidean_distance(P, Q):
returnreturn np.sqrt(np.sum((P - Q) ** 2, axis=1))
# 示例点云
P = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
Q = np.array([[1, 2, 3],
[4, 5, 6],
[8, 9, 10]])
# 计算欧氏距离
distances = euclidean_distance(P, Q)
print("Euclidean distances:", distances)