代码随想录day21｜530.二叉搜索树的最小绝对差｜501.二叉搜索树中的众数｜236. 二叉树的最近公共祖先｜Golang

代码随想录day21

坚持好累啊

目录

530.二叉搜索树的最小绝对差

501.二叉搜索树中的众数

236、二叉树的公共祖先

---

530.二叉搜索树的最小绝对差

        给你一棵所有节点为非负值的二叉搜索树，请你计算树中任意两节点的差的绝对值的最小值。

示例：

提示：树中至少有 2 个节点

思路：

        题目中要求在二叉搜索树上任意两节点的差的绝对值的最小值。

        注意是二叉搜索树，二叉搜索树可是有序的。

        遇到在二叉搜索树上求什么最值啊，差值之类的，就把它想成在一个有序数组上求最值，求差值，这样就简单多了

递归：

        那么二叉搜索树采用中序遍历，其实就是一个有序数组

        在一个有序数组上求两个数最小差值，这是不是就是一道送分题了。

        最直观的想法，就是把二叉搜索树转换成有序数组，然后遍历一遍数组，就统计出来最小差值了。

代码如下：

var slice []int
func getMinimumDifference(root *TreeNode) int {
    slice = []int{}
    inorder(root)
    minV := math.MaxInt64
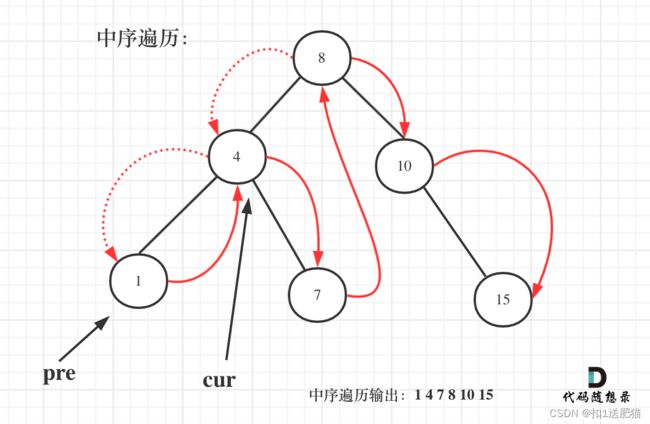
    for i:=1;i

        以上代码是把二叉搜索树转化为有序数组了，其实在二叉搜素树中序遍历的过程中，我们就可以直接计算了。需要用一个pre节点记录一下cur节点的前一个节点。

如图：

        一些同学不知道在递归中如何记录前一个节点的指针，其实实现起来是很简单的，大家只要看过一次，写过一次，就掌握了。

代码如下：

var min int 
var prev *TreeNode
func getMinimumDifference(root *TreeNode) int {
    min = math.MaxInt64 // init
    prev = nil //init
    digui(root) // dfs
    return min  // ans
}

func digui(root *TreeNode) {
    if root == nil {
        return  
    }
    digui(root.Left)     // left
    if prev != nil && root.Val - prev.Val < min {
        min = root.Val - prev.Val
    }
    prev = root // middle, 记录当前节点，用来给下一个节点做比较的
    digui(root.Right)   // right
}

本题小结：

        遇到在二叉搜索树上求什么最值，求差值之类的，都要思考一下二叉搜索树可是有序的，要利用好这一特点。

        同时要学会在递归遍历的过程中如何记录前后两个指针，这也是一个小技巧，学会了还是很受用的。

501.二叉搜索树中的众数

        给定一个有相同值的二叉搜索树（BST），找出 BST 中的所有众数（出现频率最高的元素）。

假定 BST 有如下定义：

• 结点左子树中所含结点的值小于等于当前结点的值
• 结点右子树中所含结点的值大于等于当前结点的值
• 左子树和右子树都是二叉搜索树

例如：

给定 BST [1,null,2,2],

返回[2].

提示：如果众数超过1个，不需考虑输出顺序

进阶：你可以不使用额外的空间吗？（假设由递归产生的隐式调用栈的开销不被计算在内）

思路：

        这道题目呢，递归法我从两个维度来讲。

        首先如果不是二叉搜索树的话，应该怎么解题，是二叉搜索树，又应该如何解题，两种方式做一个比较，可以加深大家对二叉树的理解

递归法：

        如果不是二叉搜索树，最直观的方法一定是把这个树都遍历了，用map统计频率，把频率排个序，最后取前面高频的元素的集合。

具体步骤如下：

1、这个树都遍历了，用map统计频率

        至于用前中后序那种遍历也不重要，因为就是要全遍历一遍，怎么个遍历法都行，层序遍历都没毛病！

这里采用前序遍历，代码如下：

a_map := make(map[int]int,0)
func searchBST(root *TreeNode, a_map *map[int]int ) { // 前序遍历
    if root == nil {
        return    
    }
    a_map[root.Val] += 1 // 统计元素频率
    searchBST(root.Left, a_map)
    searchBST(root.Right, a_map)
    return 
}

2、把统计的出来的出现频率（即map中的value）排个序

略，后面补。

3、取前面高频的元素

略，后面补。

重点先看这个利用二叉搜索树性质的答案。

二叉搜索树解法：

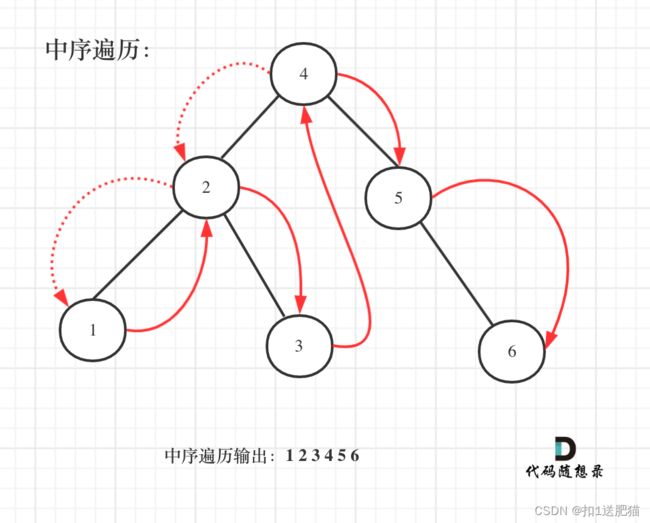
        既然是搜索树，它中序遍历就是有序的。

如图：

 中序遍历代码如下：

func travel(root *TreeNode) {
    if root == nil {
        return    
    }
    travel(root.Left)
    处理节点
    travel(root.Right)
}

        遍历有序数组的元素出现频率，从头遍历，那么一定是相邻两个元素作比较，然后就把出现频率最高的元素输出就可以了。

        关键是在有序数组上的话，好搞，在树上怎么搞呢？

这就考察对树的操作了。

在二叉树：搜索树的最小绝对差

• 中我们就使用了pre指针和cur指针的技巧，这次又用上了。
• 弄一个指针指向前一个节点，这样每次cur（当前节点）才能和pre（前一个节点）作比较。
• 而且初始化的时候pre = NULL，这样当pre为NULL时候，我们就知道这是比较的第一个元素。代码如下：

if prev == nil {    // 第一个节点
    count = 1    // 频率为1
} else if prev.Val == root.Val {    // 与前一个节点数值相同
    count += 1
} else if prev.Val != root.Val {   // 与前一个节点数值不同
    count = 1
}
prev = root     // 更新上一个节点

        此时又有问题了，因为要求最大频率的元素集合（注意是集合，不是一个元素，可以有多个众数），如果是数组上大家一般怎么办？

        应该是先遍历一遍数组，找出最大频率（maxCount），然后再重新遍历一遍数组把出现频率为maxCount的元素放进集合。（因为众数有多个）

        这种方式遍历了两遍数组。

        那么我们遍历两遍二叉搜索树，把众数集合算出来也是可以的。但这里其实只需要遍历一次就可以找到所有的众数。

那么如何只遍历一遍呢？

        如果 频率count 等于 maxCount（最大频率），当然要把这个元素加入到结果集中（以下代码为result数组），代码如下：

func findMode(root *TreeNode) []int {
    res := make([]int, 0)
    count := 1
    max := 1
    var prev *TreeNode  // 用来记录前一个node
    var travel func(node *TreeNode) 
    travel = func(node *TreeNode) {
        if node == nil {
            return
        }
        travel(node.Left)   // 左
        if prev != nil && prev.Val == node.Val {    // 如果上一个和当前这个相等
            count++ // 计数
        } else {
            count = 1   // 如果不同，则重新计算
        }
        if count >= max {   // 如果count大于max，说明要更新max了
            if count > max {    // 更新res，记录最大的
                res = []int{node.Val}
            } else if count == max {    // 记录重复的相同数量的
                res = append(res, node.Val)
            }
            max = count // 更新max
        }
        prev = node // 将当前赋给prev，用于下一次prev和node进行比较。
        travel(node.Right)  // 右
    }
    travel(root)
    return res
}

236、二叉树的公共祖先

        给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

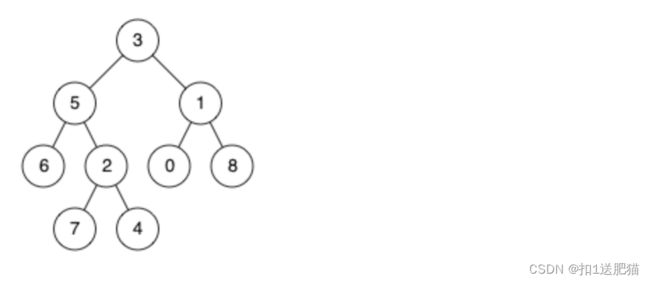
例如，给定如下二叉树:  root = [3,5,1,6,2,0,8,null,null,7,4]

示例 1:输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1输出: 3解释: 节点 5 和节点 1 的最近公共祖先是节点 3

思路:

        遇到这个题目首先想的是要是能自底向上查找就好了，这样就可以找到公共祖先了。

        那么二叉树如何可以自底向上查找呢？回溯啊，二叉树回溯的过程就是从低到上。后序遍历就是天然的回溯过程，最先处理的一定是叶子节点。

        接下来就看如何判断一个节点是节点q和节点p的公共公共祖先呢。

        首先最容易想到的一个情况：如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者 左子树出现结点q，右子树出现节点p，那么该节点就是节点p和q的最近公共祖先。

        但是很多人容易忽略一个情况，就是节点本身p(q)，它拥有一个子孙节点q(p)。

        使用后序遍历，回溯的过程，就是从低向上遍历节点，一旦发现满足第一种情况的节点，就是最近公共节点了。

        但是如果p或者q本身就是最近公共祖先呢？

        其实只需要找到一个节点是p或者q的时候，直接返回当前节点，无需继续递归子树。

        如果接下来的遍历中找到了后继节点满足第一种情况则修改返回值为后继节点，否则，继续返回已找到的节点即可。

        为什么满足第一种情况的节点一定是p或q的后继节点呢?大家可以仔细思考一下。

递归三部曲：

1、确定递归函数返回值以及参数：

        需要递归函数返回值，来告诉我们是否找到节点q或者p，那么返回值为bool类型就可以了。

        但我们还要返回最近公共节点，可以利用上题目中返回值是TreeNode * ，那么如果遇到p或者q，就把q或者p返回，返回值不为空，就说明找到了q或者p。

2、确定终止条件：

        如果找到了 节点p或者q，或者遇到空节点，就返回。

3、确定单层递归逻辑：

        值得注意的是 本题函数有返回值，是因为回溯的过程需要递归函数的返回值做判断，但本题我们依然要遍历树的所有节点。

        我们在二叉树：递归函数究竟什么时候需要返回值，什么时候不要返回值？中说了 递归函数有返回值就是要遍历某一条边，但有返回值也要看如何处理返回值！

        如果递归函数有返回值，如何区分要搜索一条边，还是搜索整个树呢？

搜索一条边的写法：

if (递归函数(root->left)) return ;

if (递归函数(root->right)) return ;

搜索整个树写法：

left = 递归函数(root->left);
right = 递归函数(root->right);
left与right的逻辑处理;

看出区别了没？

        在递归函数有返回值的情况下：如果要搜索一条边，递归函数返回值不为空的时候，立刻返回，如果搜索整个树，直接用一个变量left、right接住返回值，这个left、right后序还有逻辑处理的需要，也就是后序遍历中处理中间节点的逻辑（也是回溯）。

        那么为什么要遍历整棵树呢？直观上来看，找到最近公共祖先，直接一路返回就可以了。

如图：

        就像图中一样直接返回7，多美滋滋。

        但事实上还要遍历根节点右子树（即使此时已经找到了目标节点了），也就是图中的节点4、15、20。

        因为在如下代码的后序遍历中，如果想利用left和right做逻辑处理， 不能立刻返回，而是要等left与right逻辑处理完之后才能返回。

left = 递归函数(root->left);
right = 递归函数(root->right);
left与right的逻辑处理;

        所以此时大家要知道我们要遍历整棵树（后序遍历是这样的）。知道这一点，对本题就有一定深度的理解了。

        那么先用left和right接住左子树和右子树的返回值，代码如下：

TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);

        如果left 和 right都不为空，说明此时root就是最近公共节点。这个比较好理解

        如果left为空，right不为空，就返回right，说明目标节点是通过right返回的，反之依然。

        这里有的同学就理解不了了，为什么left为空，right不为空，目标节点通过right返回呢？

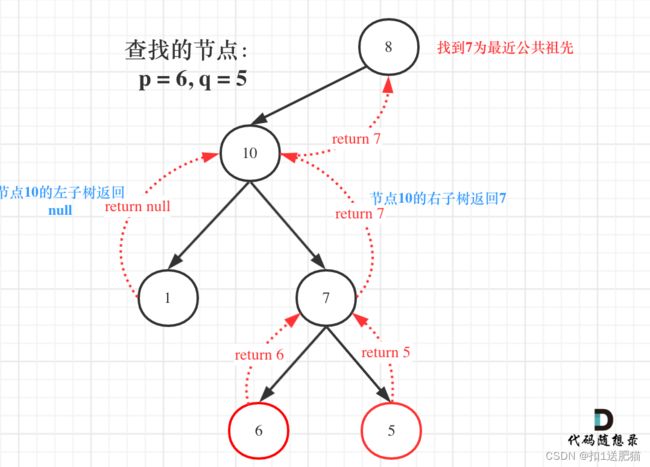
如图：

        图中节点10的左子树返回null，右子树返回目标值7，那么此时节点10的处理逻辑就是把右子树的返回值（最近公共祖先7）返回上去！

        这里点也很重要，可能刷过这道题目的同学，都不清楚结果究竟是如何从底层一层一层传到头结点的。

        那么如果left和right都为空，则返回left或者right都是可以的，也就是返回空。

代码如下：

if (left == NULL && right != NULL) return right;
else if (left != NULL && right == NULL) return left;
else  { //  (left == NULL && right == NULL)
    return NULL;
}

那么寻找最小公共祖先，完整流程图如下：

        从图中，大家可以看到，我们是如何回溯遍历整棵二叉树，将结果返回给头结点的！

整体代码如下：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
  if root == nil || root == p || root == q {    // 例如 [1，2，3],p=1,或者q=1,那么root=p/q了
    return root
  }
  left_tree := lowestCommonAncestor(root.Left, p, q)    // 递归寻找左子树符合条件的p或q
  right_tree := lowestCommonAncestor(root.Right, p, q)  // 递归寻找右子树符合条件的p或q
  
  if left_tree != nil && right_tree != nil {    // 第一种就是p和q分别在不同的子树
    return root
  }
  // 第二种-1 就是 node 即为节点 p，q 在节点 p 的左子树或右子树中。
  // 第二种—2 就是 node 即为节点 q，p 在节点 q 的左子树或者右子树中
  if left_tree != nil {   
    return left_tree
  }
  if right_tree != nil {   
    return right_tree
  }
  return nil
}

本题小结

        这道题目刷过的同学未必真正了解这里面回溯的过程，以及结果是如何一层一层传上去的。

那么我给大家归纳如下三点：

1. 求最小公共祖先，需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯，整颗树）实现从低向上的遍历方式。

2. 在回溯的过程中，必然要遍历整棵二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的返回值（也就是代码中的left和right）做逻辑判断。

3. 要理解如果返回值left为空，right不为空为什么要返回right，为什么可以用返回right传给上一层结果。

可以说这里每一步，都是有难度的，都需要对二叉树，递归和回溯有一定的理解。本题没有给出迭代法，因为迭代法不适合模拟回溯的过程。理解递归的解法就够了。