《矩阵论》学习笔记
目录
-
- 线性代数引论
-
-
- 线性空间
- 线性变换及矩阵
- Jordan标准型
- 欧式空间和酉空间
- 最小二乘法
-
- 矩阵的分解
-
-
- 三角分解
- QR分解
- 正规矩阵及Schur分解
- 满秩分解
- 奇异值分解
- 单纯矩阵的谱分解
-
- 矩阵的广义逆
-
-
- 广义逆矩阵
- 广义逆矩阵 A + A^+ A+
- A + A^+ A+的几种基本求法
- 广义逆与线性方程组
-
-
- 线性方程组的相容性、通解与 A { 1 } A\{1\} A{1}
- 相容线性方程组的最小范数解与 A { 1 , 4 } A\{1,4\} A{1,4}
- 不相容方程组的最小二乘解与 A { 1 , 3 } A\{1,3\} A{1,3}
- 不相容方程组的最小范数最小二乘解与 A + A^+ A+
-
-
- 矩阵分析
-
-
- 向量与矩阵的范数
- 特征值估计
- 矩阵级数
- 矩阵函数及其计算
-
-
- 矩阵函数的计算法(一)
- 矩阵函数的计算法(二)
-
-
线性代数引论
线性空间
加群的定义:

例如在数的乘法运算下,加群中的零元就应该是1,此时 ( Z \ { 0 } , ⋅ ) (\mathbb{Z} \backslash \{0\},\cdot) (Z\{0},⋅)不构成加群,因为负元不一定存在。
一个数集中任意两个数的和,差,积,商仍在该数集中(对四则运算封闭),则称该数集为数域,例如 Q \mathbb{Q} Q, R \mathbb{R} R, C \mathbb{C} C均为数域。
线性空间的定义:

线性相关和线性无关的定义略。
维数的定义:

基底的定义:

由定义可以得到推论:对于有限维空间 V V V, d i m V = n ⟺ V 的任一基底的元素个数都为 n dimV=n \iff V的任一基底的元素个数都为n dimV=n⟺V的任一基底的元素个数都为n。
坐标的定义:

过渡矩阵的定义:

过渡矩阵是可逆的。
取 x ∈ V \bf{x}\in V x∈V,设 x \mathbf{x} x在基 x 1 , … , x n \mathbf{x_1,\dots,x_n} x1,…,xn和 y 1 , … , y n \mathbf{y_1,\dots,y_n} y1,…,yn下的坐标分别为 ( ξ 1 , … , ξ n ) T (\xi_1,\dots,\xi_n)^T (ξ1,…,ξn)T和 ( η 1 , … , η n ) T (\eta_1,\dots,\eta_n)^T (η1,…,ηn)T,那么有:
( y 1 , … , y n ) = ( x 1 , … , x n ) A ( ξ 1 , … , ξ n ) T = A ( η 1 , … , η n ) T \begin{aligned} (\mathbf{y_1,\dots,y_n})&=(\mathbf{x_1,\dots,x_n})\mathbf{A} \\ (\xi_1,\dots,\xi_n)^T &= \mathbf{A}(\eta_1,\dots,\eta_n)^T \end{aligned} (y1,…,yn)(ξ1,…,ξn)T=(x1,…,xn)A=A(η1,…,ηn)T
子空间的定义: W ⊆ V W \subseteq V W⊆V,且 W W W也是线性空间,那么 W W W是 V V V的子空间。
交空间与和空间的定义和定理:


如果 W 1 ∩ W 2 = { θ } W_1 \cap W_2=\{\theta\} W1∩W2={θ},那么 W 1 + W 2 W_1+W_2 W1+W2是直和,记作 W 1 ⨁ W 2 W_1\bigoplus W_2 W1⨁W2。
线性变换及矩阵
线性变换反映了线性空间之间的联系。其定义为:

常见的具有几何意义的变换,例如伸缩、旋转、反射、投影都是线性变换。平移不是线性变换。
核空间、像空间及亏加秩定理:

这里引入 L L L是为了后面的叙述方便, T ∈ L ( V , W ) T\in L(V,W) T∈L(V,W)就表示 T 是 V 到 W 的线性变换 T是V到W的线性变换 T是V到W的线性变换。 θ \theta θ是 W W W中的零元。核空间维数加上像空间维数等于定义域维数。
线性变换的矩阵:设 d i m V = n dimV=n dimV=n, T ∈ L ( V , V ) T\in L(V,V) T∈L(V,V),取定 V V V的一组基 e 1 , … , e n \mathbf{e}_1,\dots,\mathbf{e}_n e1,…,en,令
T e j = a 1 j e 1 + ⋯ + a n j e n , 1 ≤ j ≤ n , T\mathbf{e}_j=a_{1j}\mathbf{e}_1+\dots+a_{nj}\mathbf{e}_n, \ 1\le j\le n, Tej=a1je1+⋯+anjen, 1≤j≤n,
采用矩阵记法得到 T ( e 1 , … , e n ) = ( e 1 , … , e n ) A T(\mathbf{e}_1,\dots,\mathbf{e}_n)=(\mathbf{e}_1,\dots,\mathbf{e}_n)\mathbf{A} T(e1,…,en)=(e1,…,en)A,则称 A \mathbf{A} A为线性变换 T T T的矩阵。
L ( V , V ) L(V,V) L(V,V)与 F n × n F^{n\times n} Fn×n存在一一对应关系,因此某个线性空间上的线性变换存在唯一一个矩阵与之对应。
线性空间同构的定义:

同构的线性空间具有完全一致的空间结构和各种运算律。线性空间同构 ⟺ \iff ⟺维数相等。
所以相似矩阵反映的是同一个线性变换。
特征值和特征向量:

用线性变换 T T T的矩阵 A \mathbf{A} A来代数计算特征值和特征向量,可得:
方程有解,说明行列式为0:

另外,相似矩阵有相同的特征多项式及特征值。
根据特征多项式可知, ∣ A ∣ = ∏ i = 1 n λ i |\mathbf{A}|=\prod\limits_{i=1}^{n}{\lambda_i} ∣A∣=i=1∏nλi , t r ( A ) = ∑ i = 1 n λ i tr(\mathbf{A})=\sum\limits_{i=1}^n{\lambda_i} tr(A)=i=1∑nλi 。
Schur引理:

Hamilton-Cayley定理 :

Cayley定理对一般数域 F F F的矩阵仍然成立。从Cayley定理可以看出,任何一个矩阵 A A A都存在使其零化的多项式,由此有如下定义和定理:

也就是说 A A A的最小零化多项式可以整除任一零化多项式,且最小零化多项式与特征多项式有相同的根。
关于属于不同特征值的特征向量之间,有如下定理:
一些其它定理:
- t r ( A B ) = t r ( B A ) tr(AB)=tr(BA) tr(AB)=tr(BA);
- 相似矩阵具有相同的特征值;
Jordan标准型
可对角化矩阵(单纯矩阵)的定义(注意是相似):

可对角化矩阵的特征:

由定理1还可以得到推论:
- 矩阵可对角化等价于它的每个特征值的几何重数等于代数重数。
- 若矩阵 A \mathbf{A} A有 n n n个互异的特征值,那么它必然可以对角化。
- 可对角化 ⟺ \iff ⟺ 最小多项式无重根。
λ − 矩阵 \mathbf{\lambda-矩阵} λ−矩阵的定义:

平时的数字矩阵是特殊的 λ − 矩阵 \lambda-矩阵 λ−矩阵。它的秩定义为:

一个定理:

无论如何初等变换, A ( λ ) A(\lambda) A(λ)的最终的Smith标准形是不变的,其中的 d i ( λ ) d_i(\lambda) di(λ)称为不变因子。因此若 A ( λ ) ≅ B ( λ ) A(\lambda)\cong B(\lambda) A(λ)≅B(λ),那么两者的不变因子也相同,反之亦然。
以下在复数域上讨论, C \mathbb{C} C上的多项式都可以分解为一次因子的幂的乘积,设 A ( λ ) A(\lambda) A(λ)的不变因子的分解为

由此引入如下定义:

根据初等因子、秩、等价的概念可以得到如下定理:
也就是说,两个 λ − 矩阵 \mathbf{\lambda-矩阵} λ−矩阵等价 ⟺ \iff ⟺两者有相同的初等因子组并且秩相等。
在实际求初等因子组时,可以先将 A ( λ ) A(\lambda) A(λ)化为对角形式(不一定要标准形),再分解因子即可,这依赖于如下结论
另外还有一个方阵相似的定理:

给定对角矩阵,如何求其不变因子(Smith标准形)?
将初等因子按照类别降幂排列,不变因子取同一等级幂的乘积。
例如求 A ( λ ) ≅ d i a g { λ ( λ + 1 ) , λ 2 , ( λ + 1 ) 2 , λ ( λ − 1 ) } A(\lambda)\cong diag\{\lambda(\lambda+1),\lambda^2,(\lambda+1)^2,\lambda(\lambda-1)\} A(λ)≅diag{λ(λ+1),λ2,(λ+1)2,λ(λ−1)} 的初等因子和不变因子:显然其初等因子有: λ , ( λ + 1 ) , λ 2 , ( λ + 1 ) 2 , λ , ( λ − 1 ) \lambda,(\lambda+1),\lambda^2,(\lambda+1)^2,\lambda,(\lambda-1) λ,(λ+1),λ2,(λ+1)2,λ,(λ−1),按照类别降幂排列得:
λ 2 λ λ 1 ( λ + 1 ) 2 ( λ + 1 ) 1 1 ( λ − 1 ) 1 1 1 \begin{matrix} \lambda^2 & \lambda&\lambda&1 \\ (\lambda+1)^2 & (\lambda+1)&1&1\\ (\lambda-1)&1&1&1 \end{matrix} λ2(λ+1)2(λ−1)λ(λ+1)1λ11111
因此不变因子为: d 4 ( λ ) = λ 2 ( λ + 1 ) 2 ( λ − 1 ) , d 3 ( λ ) = λ ( λ + 1 ) , d 2 ( λ ) = d 1 ( λ ) = 1 d_4(\lambda)=\lambda^2(\lambda+1)^2(\lambda-1),d_3(\lambda)=\lambda(\lambda+1),d_2(\lambda)=d_1(\lambda)=1 d4(λ)=λ2(λ+1)2(λ−1),d3(λ)=λ(λ+1),d2(λ)=d1(λ)=1。
接下来就是重头戏,Jordan标准形(以及Jordan块)的定义:

注意 J J J是上三角阵。有 Jordan标准形定理:
A ∼ J A \sim J A∼J
根据Jordan标准形的定义,我们可以推出: A A A可对角化,当且仅当 λ I − A \lambda I-A λI−A的初等因子都是一次的。
利用 λ I − A \lambda I-A λI−A的Smith标准形,可以很简单的得到 A A A的最小多项式:

由此我们得到如下判定可对角化的推论:

欧式空间和酉空间
在实际问题中线性空间存在不够完善,因此需要将度量性质引入线性空间。
欧式(Euclid)空间的定义:

欧式空间的一些性质,例如:模、三角不等式、柯西不等式、正交、标准正交基、基的度量矩阵等,不作详细说明。
Schmidt正交化方法:
先正交化

再单位化。
两个欧式子空间正交,表示各自任取一个向量,这两个向量正交;这等价于基相互正交。一个定理:
正交变换的定义:

正交变换不改变长度、距离、角度。关于正交变换,以下命题等价:
- T T T是正交变换;
- ∀ x ∈ V , ∣ ∣ T x ∣ ∣ = ∣ ∣ x ∣ ∣ \forall x\in V, ||Tx||=||x|| ∀x∈V,∣∣Tx∣∣=∣∣x∣∣;
- 若 e 1 , … , e n e_1,\dots,e_n e1,…,en是 V V V的标准正交基,则 T e 1 , … , T e n Te_1,\dots,Te_n Te1,…,Ten也是 V V V的标准正交基;
- T T T在 V V V的标准正交基下的矩阵 Q Q Q满足 Q T = Q − 1 Q^T=Q^{-1} QT=Q−1。
酉空间的定义与欧式空间类似,欧式空间为有限维实内积空间,酉空间则为有限维复内积空间。两者有完全平行的理论:

酉空间上的内积形式一般为 ( x , y ) = y H x = ( y ‾ ) T x (x,y)=y^Hx=(\overline{y})^Tx (x,y)=yHx=(y)Tx。
酉空间的一些性质:

A A A为酉矩阵 ⟺ A − 1 = A H ⟺ \iff A^{-1}=A^H \iff ⟺A−1=AH⟺ A A A的列向量都是单位向量且两两正交。
最小二乘法
已知 y = k 1 x 1 + ⋯ + k n x n y=k_1x_1+\dots +k_nx_n y=k1x1+⋯+knxn,进行了 m ≥ n m\ge n m≥n次试验得到了 m m m组数据:
- A = ( a 1 , … a n ) A=(a_1,\dots a_n) A=(a1,…an),其中 a i = ( x i ( 1 ) , … , x i ( m ) ) T a_i=(x_i^{(1)},\dots,x_i^{(m)})^T ai=(xi(1),…,xi(m))T;
- b = ( y ( 1 ) , … , y ( m ) ) T b=(y^{(1)},\dots,y^{(m)})^T b=(y(1),…,y(m))T。
设 k = ( k 1 , … , k n ) T k=(k_1,\dots,k_n)^T k=(k1,…,kn)T,求解参数 k k k等价于求 b b b在酉空间 s p a n { a 1 , … , a n } span\{a_1,\dots,a_n\} span{a1,…,an}上的最佳逼近(投影)。
亦即求解 A H A k = A H b A^HAk=A^Hb AHAk=AHb。
矩阵的分解
三角分解
单位上三角矩阵:上三角矩阵的对角线全为1 。
单位上三角矩阵的乘积仍然是单位上三角矩阵,逆也是。
LR分解定理:设 A ∈ C n × n A\in\mathbb{C}^{n\times n} A∈Cn×n是非奇异矩阵(满秩、可逆、行列式非零),则存在唯一的单位下三角矩阵 L L L和上三角矩阵 R R R使得 A = L R A=LR A=LR的充分必要条件是 A A A的顺序主子式均非零(定理中上下可交换)。
LR分解方法:

根据LR分解里面的 R R R,考虑到

进而可以得到LDR分解: A = L D R A=LDR A=LDR,其中 L L L和 R R R都是单位三角矩阵。
Hermite矩阵:自共轭矩阵,即 a i j ‾ = a j i \overline{a_{ij}}=a_{ji} aij=aji。
正定矩阵 ⟺ \iff ⟺矩阵的所有顺序主子式大于0 。
Cholesky分解:设 A ∈ C n × n A\in\mathbb{C}^{n\times n} A∈Cn×n是Hermite正定矩阵,则存在下三角矩阵 G G G,使得 A = G G H A=GG^H A=GGH。
QR分解

这个定理中的QR矩阵可以通过Schmidt正交化来求得:

而唯一性也很好证明。
设 u ∈ C n u\in\mathbb{C}^n u∈Cn为单位向量,即 u H u = 1 u^Hu=1 uHu=1,称 H = I − 2 u u H H=I-2uu^H H=I−2uuH为Householder矩阵(初等反射矩阵),由 H H H确定的变换 y = H x y=Hx y=Hx称为Householder变换(初等反射变换)。Householder矩阵的性质:
- H H = H , H H H = I = H 2 H^H=H,H^HH=I=H^2 HH=H,HHH=I=H2;
- H − 1 = H H^{-1}=H H−1=H;
- ∣ H ∣ = − 1 |H|=-1 ∣H∣=−1。
一个定理:设 e e e是单位向量, ∀ x ∈ C n \forall x\in\mathbb{C}^n ∀x∈Cn,存在Householder矩阵 H H H,使得 H x = ρ e Hx=\rho e Hx=ρe,其中 ρ = ∣ ∣ x ∣ ∣ 2 \rho =||x||_2 ρ=∣∣x∣∣2,且 ρ x H e \rho x^H e ρxHe是实数。
正规矩阵及Schur分解
Schur引理:方阵(酉/正交)相似于上三角阵

正规矩阵的定义:

A A A是正规矩阵 ⟺ \iff ⟺ A A A酉相似于对角阵( U H A U = d i a g { λ 1 , . . . , λ n } U^HAU=diag\{\lambda_1,...,\lambda_n\} UHAU=diag{λ1,...,λn})。
关于正规矩阵的一些推论:


推论3:正规三角矩阵是对角矩阵。
实对称阵 A A A正交相似于对角阵( Q T A Q = d i a g { λ 1 , . . . , λ n } Q^TAQ=diag\{\lambda_1,...,\lambda_n\} QTAQ=diag{λ1,...,λn}),如何求这个正交阵 Q Q Q呢?
对于 A A A的每个特征值 λ \lambda λ,求 ( λ I − A ) x = 0 (\lambda I-A)x=0 (λI−A)x=0的解空间的基础解系,然后Schmidt正交化为单位正交向量,每个特征值的结果作为列向量拼在一起,就得到了 Q Q Q。
满秩分解
满秩分解表示任一矩阵可以分解为列满秩和行满秩矩阵的乘积:

Hermite标准形:

计算Hermite标准形的方式:

原矩阵 A A A和其Hermite标准形 A ^ r \hat{A}_r A^r的列向量组具有完全一样的线性关系(线性组合得到零向量的系数一致)。
满秩分解的方式:

奇异值分解
首先介绍了一个引理:

任取 P ∈ C m × n , Q ∈ C n × m P\in\mathbb{C}^{m\times n},Q\in\mathbb{C}^{n\times m} P∈Cm×n,Q∈Cn×m,根据换位公式 ∣ λ I − P Q ∣ = λ ∣ m − n ∣ ∣ λ I − Q P ∣ |\lambda I-PQ|=\lambda^{|m-n|}|\lambda I-QP| ∣λI−PQ∣=λ∣m−n∣∣λI−QP∣,很容易发现两者具有相同的非零特征值,半正定也直接代入验证即可。
因为 A H A A^HA AHA半正定,因此其特征值也不小于零,由此有奇异值的定义:

奇异值分解:

奇异值分解的基本步骤:

上面的(以红色横线分割)两种分解方法,实际上是考虑 m m m和 n n n的大小关系,也就是 A A H AA^H AAH和 A H A A^HA AHA的矩阵大小关系,可以选择更容易计算的方法。
极分解:

单纯矩阵的谱分解
回顾:单纯矩阵就是可对角化矩阵,即可相似于对角矩阵。
定义:设 A ∈ C n × n A\in\mathbb{C}^{n\times n} A∈Cn×n,若 A 2 = A A^2=A A2=A,则称 A A A为幂等阵(或投影阵,投影变换的矩阵就是幂等阵)。
A A A为幂等阵 ⟺ \iff ⟺ r ( A ) + r ( I − A ) = n r(A)+r(I-A)=n r(A)+r(I−A)=n。
关于幂等阵的一些性质:

谱分解、谱阵:

谱分解的一般步骤:

关于谱分解的一些推论:

上面第2个推论在矩阵函数中有重要应用。
因为正规矩阵也是单纯矩阵,因此正规矩阵也可以谱分解,它的谱分解的等价关系中,描述为:…… A A A是正规阵 ⟺ \iff ⟺存在 k k k个幂等厄尔米特矩阵 G 1 , . . . , G k G_1,...,G_k G1,...,Gk,……(剩下的描述参见上文)
幂等阵对应投影变换,而幂等厄尔米特阵对应正交投影变换。
正规矩阵的谱分解过程可以简化(也就是不用求逆,因为酉矩阵的逆等于共轭转置):

事实上,正规矩阵 A A A可以酉相似于特征值对角阵,写作 A = U d i a g { λ 1 , . . . , λ n } U H A=Udiag\{\lambda_1,...,\lambda_n\}U^H A=Udiag{λ1,...,λn}UH,令 G i = U i U i H G_i=U_iU_i^H Gi=UiUiH,这就是 A A A的谱分解,只是有些重根可以化简。
矩阵的广义逆
本章介绍的是 m × n m\times n m×n矩阵的Penrose广义逆 A + A^+ A+。
广义逆矩阵
广义逆矩阵的定义:

注意这四个方程只需满足一个或以上就可以称为广义逆矩阵。因此共有15类广义逆。假设 G G G满足第 i , j i,j i,j两个方程,则记为 G = A ( i , j ) G=A^{(i,j)} G=A(i,j),满足所有方程则记为 G = A ( 1 , 2 , 3 , 4 ) G=A^{(1,2,3,4)} G=A(1,2,3,4),以此类推。
其中, A ( 1 , 2 , 3 , 4 ) = A + A^{(1,2,3,4)}=A^+ A(1,2,3,4)=A+是存在且唯一的,其它各类广义逆不唯一,每类广义逆包含的矩阵集合记作 A { i } , A { i , j } A\{i\},A\{i,j\} A{i},A{i,j}等,有 A ( i ) ∈ A { i } A^{(i)}\in A\{i\} A(i)∈A{i}。
15类广义逆中较常见的是 A { 1 } , A { 1 , 3 } , A { 1 , 4 } A\{1\},A\{1,3\},A\{1,4\} A{1},A{1,3},A{1,4}以及 A + A^+ A+。
A { 1 } A\{1\} A{1}也叫作 { 1 } 逆 \{1\}逆 {1}逆,也叫作减号逆,常记作 A − A^- A−;而 A + A^+ A+也叫作加号逆或伪逆。
广义逆矩阵 A + A^+ A+
A + A^+ A+的定义(上一节有阐述了):
当 A A A是一个方阵 A ∈ C n × n A\in\mathbb{C}^{n\times n} A∈Cn×n 且 ∣ A ∣ ≠ 0 |A|\neq 0 ∣A∣=0,则 A + = A − 1 A^+=A^{-1} A+=A−1。
一个存在性定理:对任意 A ∈ C n × n A\in\mathbb{C}^{n\times n} A∈Cn×n, A + A^+ A+存在且唯一。也就是说方阵一定存在唯一的加号逆。(实际上把 A A A奇异值分解,每一部分取逆即可)
关于方阵 A + A^+ A+的一些性质:

关于常数 λ \lambda λ的加号逆 λ + \lambda^+ λ+以及对角矩阵的加号逆的说明:

A + A^+ A+的几种基本求法
满秩分解求 A + A^+ A+:

当 A A A本身就列满秩,即 n = r n=r n=r时,满秩分解可以写成 A = A I n = F G A=AI_n=FG A=AIn=FG,此时 A + = ( A H A ) − 1 A H A^+=(A^HA)^{-1}A^H A+=(AHA)−1AH;
当 A A A本身就行满秩,即 m = r m=r m=r时,满秩分解可以写成 A = I m A = F G A=I_mA=FG A=ImA=FG,此时 A + = A H ( A A H ) − 1 A^+=A^H(AA^H)^{-1} A+=AH(AAH)−1。
奇异值分解求 A + A^+ A+(繁琐,一般用下面简化版的方法):

更加简化的奇异值分解求 A + A^+ A+的方法:

因此求 A + A^+ A+可以先求 A H A A^HA AHA的 r r r个非零特征值和标准正交特征向量矩阵 U 1 U_1 U1,然后带入公式即可。
特别的,当 r ( A ) = 1 r(A)=1 r(A)=1时,即非零奇异值只有一个时,有 A + = λ 1 − 1 A H = 1 ∑ ∣ a i j ∣ 2 A H A^+=\lambda_1^{-1}A^H=\frac{1}{\sum|a_{ij}|^2}A^H A+=λ1−1AH=∑∣aij∣21AH 。
谱分解求 A + A^+ A+(Sylvester公式):
广义逆与线性方程组
考虑非齐次线性方程组 A x = b Ax=b Ax=b,其中 A ∈ C m × n A\in\mathbb{C}^{m\times n} A∈Cm×n, b ∈ C m b\in\mathbb{C}^m b∈Cm给定, x ∈ C n x\in\mathbb{C}^n x∈Cn为待求解向量,若有解则称方程组相容,否则称不相容或矛盾方程组。
根据是否相容,方程组有最小范数解、最小二乘解、最小范数最小二乘解的概念。
线性方程组的相容性、通解与 A { 1 } A\{1\} A{1}
有一个超级复杂的定理:
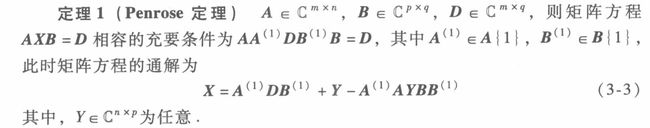
由Penrose定理得到两个推论(合理地取 A , B , D A,B,D A,B,D即可推出):


推论2给出了 A x = b Ax=b Ax=b 相容时通解的求法。
注:(别的判定方法)方程组相容的充要条件是 r ( A ) = r ( A ‾ ) r(A)=r(\overline{A}) r(A)=r(A),其中 A ‾ \overline{A} A表示增广矩阵。
因为 A + ∈ A ( 1 ) A^+\in A^{(1)} A+∈A(1),因此当 A x = b Ax=b Ax=b相容时,通解为
x = A + b + ( I − A + A ) y , y ∈ C n x=A^+b+(I-A^+A)y, \ y\in\mathbb{C}^n x=A+b+(I−A+A)y, y∈Cn
并且可以断言,相容方程 A x = b Ax=b Ax=b的解唯一当且仅当 A A A列满秩。
然后给出了 A { 1 } A\{1\} A{1}的求法:

并且可以通过初等变换来求 P P P和 Q Q Q:

注:这里的“初等变换”, A A A和 I m I_m Im是行变换, A A A和 I n I_n In是列变换。
注:当 A A A为 n n n阶可逆阵时, A { 1 } = { Q I n P } = { Q P } = A − 1 A\{1\}=\{QI_nP\}=\{QP\}=A^{-1} A{1}={QInP}={QP}=A−1,即 A { 1 } A\{1\} A{1}只有唯一的 A − 1 A^{-1} A−1。
相容线性方程组的最小范数解与 A { 1 , 4 } A\{1,4\} A{1,4}
设线性方程组 A x = b Ax=b Ax=b相容,对任意 A ( 1 , 4 ) ∈ A { 1 , 4 } A^{(1,4)}\in A\{1,4\} A(1,4)∈A{1,4}, A ( 1 , 4 ) b A^{(1,4)}b A(1,4)b都是最小范数解。注意, A { 1 , 4 } A\{1,4\} A{1,4}可能有无穷多个元,但对其中任意元, A ( 1 , 4 ) b A^{(1,4)}b A(1,4)b总是不变的,且为唯一的最小范数解。
反之若 X ∈ C n × m X\in\mathbb{C}^{n\times m} X∈Cn×m,对任意的 b ∈ C m b\in\mathbb{C}^m b∈Cm, X b Xb Xb都为相容方程组 A x = b Ax=b Ax=b的最小范数解,则必有 X ∈ A { 1 , 4 } X\in A\{1,4\} X∈A{1,4} 。
A { 1 , 4 } = { X ∣ X A = A ( 1 , 4 ) A } = { X ∣ X A = A + A } A\{1,4\}=\{X|XA=A^{(1,4)}A\}=\{X|XA=A^+A\} A{1,4}={X∣XA=A(1,4)A}={X∣XA=A+A},即 A { 1 , 4 } A\{1,4\} A{1,4}由方程 X A = A ( 1 , 4 ) A XA=A^{(1,4)}A XA=A(1,4)A的所有解构成,由此可得其通式: A { 1 , 4 } = { A ( 1 , 4 ) + Z ( I − A A ( 1 , 4 ) ) ∣ Z ∈ C n × m } A\{1,4\}=\{A^{(1,4)}+Z(I-AA^{(1,4)})|Z\in\mathbb{C}^{n\times m}\} A{1,4}={A(1,4)+Z(I−AA(1,4))∣Z∈Cn×m} 。
但是教材没有给出怎么求 A ( 1 , 4 ) A^{(1,4)} A(1,4)。
不过因为 A + ∈ A { 1 , 4 } A^+\in A\{1,4\} A+∈A{1,4},因此最小范数解的计算方式就是 x = A + b x=A^+b x=A+b。
不相容方程组的最小二乘解与 A { 1 , 3 } A\{1,3\} A{1,3}
A { 1 , 3 } = { X ∣ A X = A A ( 1 , 3 ) } = { X ∣ A X = A A + } A\{1,3\}=\{X|AX=AA^{(1,3)}\}=\{X|AX=AA^+\} A{1,3}={X∣AX=AA(1,3)}={X∣AX=AA+}
由此可得通式: A { 1 , 3 } = { A ( 1 , 3 ) + ( I − A ( 1 , 3 ) A ) Z ∣ Z ∈ C n × m } A\{1,3\}=\{A^{(1,3)}+(I-A^{(1,3)}A)Z|Z\in\mathbb{C}^{n\times m}\} A{1,3}={A(1,3)+(I−A(1,3)A)Z∣Z∈Cn×m} 。
定理:对任意的 A ( 1 , 3 ) ∈ A { 1 , 3 } A^{(1,3)}\in A\{1,3\} A(1,3)∈A{1,3}, x = A ( 1 , 3 ) b x=A^{(1,3)}b x=A(1,3)b 是不相容方程组 A x = b Ax=b Ax=b 的最小二乘解。
另外一个定理:
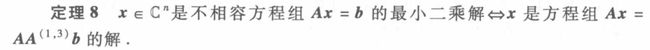
进而可以得到最小二乘解的通式:

如果 A A A是列满秩的,最小二乘解就是唯一的。
不相容方程组的最小范数最小二乘解与 A + A^+ A+
一个引理: A + = A ( 1 , 4 ) A A ( 1 , 3 ) A^+=A^{(1,4)}AA^{(1,3)} A+=A(1,4)AA(1,3) 。
最小范数最小二乘解的定理:

总结以上有如下表格:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dYv33Llr-1675669736790)(https://dragonylee-blog.oss-cn-beijing.aliyuncs.com/lenovo/202211051047727.png)]
实际上,对于方程组 A x = b Ax=b Ax=b,只要求出 A + A^+ A+,则 A + b A^+b A+b就给出了方程的各种意义下的解。
换句话说上面的讨论都没啥意义
矩阵分析
向量与矩阵的范数
向量范数的定义:

p-范数的定义:

有限维线性空间任意两种范数都是等价的,即:设 ∣ ∣ x ∣ ∣ α ||\mathbf{x}||_{\alpha} ∣∣x∣∣α和 ∣ ∣ x ∣ ∣ β ||\mathbf{x}||_{\beta} ∣∣x∣∣β是有限维线性空间 V V V中任两种范数,则存在正整数 k 1 k_1 k1和 k 2 k_2 k2,使得 ∀ x ∈ V \forall\mathbf{x}\in V ∀x∈V,都有 k 1 ∣ ∣ x ∣ ∣ β ≤ ∣ ∣ x ∣ ∣ α ≤ k 2 ∣ ∣ x ∣ ∣ β k_1||\mathbf{x}||_{\beta}\le ||\mathbf{x}||_{\alpha}\le k_2||\mathbf{x}||_{\beta} k1∣∣x∣∣β≤∣∣x∣∣α≤k2∣∣x∣∣β 。
由范数引入线性空间中极限的概念:

关于按范数收敛的两个定理:

把矩阵拍扁也可以看成是一个向量,因此上面的定义和定理都可以应用于矩阵的向量范数(广义矩阵范数),而矩阵范数(乘积范数)还需要在向量范数的三条公理上再加上一条相容性:

设 A ∈ C n × n \mathbf{A}\in\mathbb{C}^{n\times n} A∈Cn×n,则矩阵的F-范数定义为: ∣ ∣ A ∣ ∣ F = ( ∑ i , j = 1 n ∣ a i j ∣ 2 ) 1 2 = ( tr ( A H A ) ) 1 2 ||\mathbf{A}||_F=(\sum\limits_{i,j=1}^n |a_{ij}|^2)^{\frac{1}{2}}=(\text{tr}(\mathbf{A}^H\mathbf{A}))^{\frac{1}{2}} ∣∣A∣∣F=(i,j=1∑n∣aij∣2)21=(tr(AHA))21 。
F-范数有很多好的性质:

关于向量范数与矩阵范数的相容性,即是否满足 ∣ ∣ A x ∣ ∣ v ≤ ∣ ∣ A ∣ ∣ m ∣ ∣ x ∣ ∣ v ||\mathbf{A}\mathbf{x}||_v\le||\mathbf{A}||_m||\mathbf{x}||_v ∣∣Ax∣∣v≤∣∣A∣∣m∣∣x∣∣v,结论是对于任意向量范数,都存在矩阵范数与之相容,反之亦然。有如下算子范数的定义:

对于常见的三种向量范数,从属的算子范数如下:

∣ ∣ A ∣ ∣ F ||\mathbf{A}||_F ∣∣A∣∣F和 ∣ ∣ A ∣ ∣ 2 ||\mathbf{A}||_2 ∣∣A∣∣2都与 ∣ ∣ x ∣ ∣ 2 ||\mathbf{x}||_2 ∣∣x∣∣2相容,有 ∣ ∣ A ∣ ∣ 2 ≤ ∣ ∣ A ∣ ∣ F ||\mathbf{A}||_2 \le ||\mathbf{A}||_F ∣∣A∣∣2≤∣∣A∣∣F 。
矩阵的非奇异性条件:

方阵的谱半径的定义:

谱半径不大于任何一种矩阵范数,即 ρ ( A ) ≤ ∣ ∣ A ∣ ∣ \rho(\mathbf{A})\le||\mathbf{A}|| ρ(A)≤∣∣A∣∣,这个界是紧的。
特征值估计
一个定理:

前两个小定理是因为谱半径 ρ ( A ) ≤ ∣ ∣ A ∣ ∣ \rho(\mathbf{A})\le||\mathbf{A}|| ρ(A)≤∣∣A∣∣,最后一个可以由相似矩阵具有相同的迹推出,等号成立当且仅当 A \mathbf{A} A酉相似于对角阵(即正规矩阵)。
上述定理(1)(2)通过计算列范数和行范数将 A \mathbf{A} A的特征值限定在复平面的某圆盘内,为了更加精确引入盖尔圆盘(Gerschgorin)以及相关的圆盘定理:

由圆盘定理容易得到几个推论:

需要注意的是,对于实矩阵,特征值要么是实数,要么是共轭复数成对出现。
用盖尔圆盘估计特征值时,往往希望得到更多的孤立盖尔圆,通常有以下优化方法:

一个关于Hermite阵(厄尔米特阵)的Weyl定理:

Weyl定理的推论(Weyl单调定理):上述定理中若 B \mathbf{B} B是半正定的,则有 λ j ( A ) ≤ λ j ( A + B ) \lambda_j(\mathbf{A})\le\lambda_j(\mathbf{A}+\mathbf{B}) λj(A)≤λj(A+B) 。
矩阵级数
矩阵序列收敛于某一个矩阵,等价于其中每个元素收敛于某个元素,即:

矩阵级数的定义(和数列级数类似):

同样的,矩阵级数收敛等价于每个元素数值级数都收敛。
绝对收敛的定义:

绝对收敛必然收敛,另外有矩阵绝对收敛的等价条件:

收敛(绝对收敛)的矩阵级数乘上常矩阵也收敛(绝对收敛)。
关于矩阵幂级数(方阵)的基本定理:

根据上述定理的两个推论:


矩阵函数及其计算
矩阵函数的定义(矩阵函数是收敛的矩阵幂级数):

根据定义矩阵函数指的是收敛的矩阵幂级数。根据数学分析中的一些函数展开,我们可以得到对应的矩阵函数:

若将矩阵函数中的变元带上参数,有:

以下列出一些常见的矩阵指数及三角函数的性质:

有时候可以利用零化多项式计算矩阵函数。
矩阵函数的计算法(一)
若 A \mathbf{A} A为单纯矩阵,函数矩阵的求法为:

若 A \mathbf{A} A为一般矩阵,上面的结论中的 f ( λ ) f(\lambda) f(λ)要改成 f ( J ( λ ) ) f(\mathbf{J}(\lambda)) f(J(λ)),Jordan标准型的形式。具体形式非常繁琐。
矩阵函数的计算法(二)
对于一般矩阵 A \mathbf{A} A,其函数矩阵可以转换为谱上一致多项式:
