【论文阅读】SQLNet: GENERATING STRUCTURED QUERIES FROM NATURAL LANGUAGE WITHOUT REINFORCEMENT LEARNING

【论文阅读】SQLNet: GENERATING STRUCTURED QUERIES FROM NATURAL LANGUAGE WITHOUT REINFORCEMENT LEARNING

1. 来源

• https://arxiv.org/abs/1711.04436
• 2017

2. 介绍

从自然语言中合成SQL查询是一个长期存在的开放问题，最近已经引起了相当大的兴趣。

• 为了解决这个问题，现有的方法是采用一个序列到序列风格的模型。这种方法必然要求序列化SQL查询。由于同一个SQL查询可能具有多个等效的序列化，因此训练一个序列到序列风格的模型对其中一个的选择非常敏感。
  • 这种现象被记录为“秩序问题”问题。现有的最先进的方法依赖于强化学习来奖励解码器生成任何等效的序列化。然而，作者观察到，从强化学习中得到的改进是有限的。

在本文中，作者提出了一种新的方法，即 SQLNet，从根本上解决这个问题，避免顺序到序列结构时的顺序不重要。特别地，作者采用了一种基于草图的方法，其中草图包含一个依赖图，这样就可以通过只考虑它所依赖的之前的预测来完成一个预测。此外，作者提出了一个序列到集的模型以及列注意机制来合成基于草图的查询。通过结合所有这些新技术，作者证明了 SQLNet 在 WikiSQL 任务上可以比现有技术高出9%到13%。

---

3. 模型

在本节中，作者将介绍解决WikiSQL任务的SQLNet解决方案。与现有的语义解析模型（Dong & Lapata，2016）不同，它被设计为与输出语法无关，作者的基本思想是采用一个草图，它与SQL语法高度一致。因此，SQLNet 只需要填充草图中的插槽，而不必同时预测输出语法和内容。

• 草图被设计得足够通用，以便所有感兴趣的 SQL 查询都可以用草图来表示。因此，使用草图并不妨碍作者的方法的普遍性。作者将在第3.1节中解释一个草图的细节。
• 草图捕捉到了要做的预测的依赖性。通过这样做，对一个槽的值的预测只基于它所依赖的那些槽的值。这避免了序列到序列模型中的“顺序问题”问题，该模型中的一个预测是有条件的根据所有之前的预测（Vinyals等人，2016）。为了基于草图做出预测，作者开发了两种技术，序列到集和列注意。作者将在第3.2节中解释这些技术的细节。

作者结合了所有的技术来设计一个SQLNet神经网络，从一个自然语言问题和一个表模式中合成一个SQL查询。在第 3.3 节中，作者介绍了SQLNet的细节和训练细节，以在不使用强化学习的情况下超越以前的最先进的方法。

3.1 基于草图的查询合成

作者所使用的SQL草图正式显示在图 2a 中所示。

• 以粗体显示的标记（即，select、where、AND）表示SQL关键字。
• 以“$”开头的令牌表示要填充的插槽。
• “$”后面的名称表示预测的类型。
  • 例如，$AGG 插槽可以用一个空的令牌或其中一个聚合操作符来填充，如 SUM和MAX。
  • $列 和 $值 插槽需要分别填充问题的列名和子字符串。$OP插槽可以从 {=，<，>} 中取一个值。()∗ 使用正则表达式表示零或多个和子句。

该草图的依赖关系图如图 2b 所示。所有要预测值的插槽都用方框表示，每个依赖项都被描述为一条有向边。例如，OP1的框分别有来自列1的两个输入边和自然语言问题。这些边表明，对OP1 的值的预测取决于列1的值和自然语言问题。作者可以将作者的模型视为基于此依赖关系图的一个图形化模型，并将查询合成问题视为在图上的一个推理问题。从这个角度来看，作者可以看到，对一个约束的预测与另一个约束是独立的，因此作者的方法可以从根本上避免序列到序列模型中的“顺序问题”问题。

请注意，尽管它很简单，但这个草图的表现力足以表示WikiSQL任务中的所有查询。作者的 SQLNet 方法并不仅仅局限于这个草图。为了合成更复杂的SQL查询，作者可以简单地使用一个支持更丰富语法的草图。事实上，WikiSQL任务上的最新方法，即 Seq2SQL（Zhong et al.，2017），也可以被视为一种基于草图的方法。特别是，Seq2SQL对 WHERE子句分别预测 $AGG和 $列。但是，Seq2SQL使用从序列到序列的模型生成WHERE子句。因此，它仍然面临着“秩序问题”的问题。

3.2 使用列注意的序列到集的预测

在本节中，作者使用WHERE子句中的列名预测作为示例来解释序列到集模型和列注意的思想。作者将在第3.3节中解释完整的SQLNet模型。

1）序列2集合。直观地说，出现在WHERE子句中的列名构成了所有列名的完整集的子集。因此，与其生成一个列名序列，作者可以简单地预测哪些列名出现在这个感兴趣的子集中。作者将这种想法称为序列到集的预测。

特别地，作者计算了概率 $P_{wherecol}(col|Q)$，其中 col 是一个列名，Q 是自然语言问题。为了达到这个目的，一个想法是计算 $P_{wherecol}(col|Q)$ 为：

其中，σ 为 sigmoid 函数，$E_{col}$ 和 $E_Q$ 分别为列名和自然语言问题的嵌入，$u_c$ 和 $u_q$ 为可训练变量的两个列向量。在这里，嵌入的 $E_{col}$ 和 $E_Q$ 可以分别计算为运行在 col 和 Q 序列之上的双向LSTM的隐藏状态。注意编码列名的两个lstm，并且问题不共享它们的权重。$u_c、u_q、E_{col}、E_Q$的维数都为 d，这是LSTM的隐藏状态的维数。

这样做，可以通过检查 $P_{wherecol}(col|Q)$,来判断 WHERE 子句中包含特定列是否独立于其他列。

2）列关注。式 (1) 存在使用EQ的问题。由于它仅被计算为自然语言问题的隐藏状态，因此它可能无法记住在预测特定列名时有用的特定信息。例如，在图1中的问题中，令牌“数字”与预测 “No”列 更相关。在哪里的条款中。然而，令牌的“玩家”与预测选择子句中的“玩家”列更相关。在预测一个特定的列时，嵌入应该反映出自然语言问题中最相关的信息。

为了结合这种直觉，作者设计了列注意机制来计算 $E_{Q|col}，而不是 $E_Q$。特别地，作者假设 $H_Q$ 是一个d×L 的矩阵，其中 L 是自然语言问题的长度。$H_Q$ 的第 i 列表示与问题的第 i 个token 对应的LSTM的隐藏状态输出。

作者计算问题中每个token的注意权重w。特别地，w是一个 l 维的列向量，其计算方法为：

其中 $v_i$ 表示 v 的第 i 维，$H_Q^i$ 表示 $H_Q$ 的第 i 列，W是大小为 d×d 的可训练矩阵。

在计算了注意权重w后，作者可以计算出 $E_{Q|col}$ 作为每个令牌的LSTM隐藏输出的加权和，基于w：

作者可以在式(1)中 用 $E_{Q|col}$ 代替 EQ，得到列注意模型：

事实上，作者发现在σ算子之前再增加一层仿射变换可以提高预测性能约1.5%。因此，作者在WHERE子句中得到了预测列名的最终模型：

其中 $U_c^{col}$ 和 $U_q^{col}$ 是大小为d×d的可训练矩阵，$u_a^{col}$是 d 维可训练向量。

作者想强调的是，列注意是通用注意机制的一个特殊实例，用于计算基于列名的问题的注意映射。作者将在作者的评估中表明，这种机制可以比一个序列到集的模型改进大约3个点。

3.3 SQLNet 模型和训练细节

在本节中，作者将介绍完整的SQLNet模型和训练细节。如图 2b 所示，选择子句和哪里的预测子句是分开的。下面，作者首先介绍生成WHERE子句的模型，然后是SELECT子句。最后，作者描述了更多的训练细节，这有助于提高预测精度。

3.3.1 预测 where 子句

WHERE子句是WikiSQL任务中要预测的最复杂的结构。作者的SQLNet模型首先根据基于3.2节预测WHERE子句中出现的列集，然后通过预测OP和值槽为每个列生成约束。作者在下面描述它们。

1）列槽。在根据公式(3)计算 $P_{wherecol}(col|Q)$ 之后，SQLNet 需要决定在其中包括哪些列。一种方法是设置一个阈值 τ∈（0,1），以便选择所有具有 $P_{wherecol}(col|Q)$ ≥ τ 的列。

• 然而，作者发现另一种方法通常可以提供更好的性能。现在作者来解释一下这种方法。特别地，作者使用一个网络来预测子集中要包含的列的总数 K，并选择具有最高 $P_{wherecol}(col|Q)$ 的前K列来形成WHERE子句中的列名。

作者观察到，大多数查询的WHERE子句中都有有限数量的列。因此，作者为要选择的列数设置了一个上限N，因此作者将这个问题预测为一个（N+1）路分类问题（从0到N）。特别地，作者有：

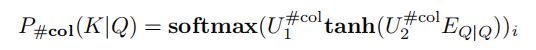
其中 $U_1^{\#col}$ 和 $U_2^{\#col}$ 分别为大小（N + 1）×d 和 d×d 的可训练矩阵。概念softmax（…）i表示softmax 输出的第 i 个维度，作者将在其余的描述中使用这个概念。SQLNet选择 K 最大化 $P_{\#col}(K|Q)$。

在作者的评估中，作者只需选择N个=4来简化作者的评估设置。但是请注意，作者可以通过使用变长度预测模型来消除超参数N，例如将在第3.3.2节中讨论的选择列预测模型。

2）OP插槽。对于WHERE子句中的每一个列，预测其OP插槽的值是一个三种方式的分类：模型需要从{=，>，<}中进行选择。因此，作者进行了计算：

其中 col 是所考虑的列，$U_1^{op}、U_c^{op}、U_q^{op}$ 分别为大小为 3×d、d×d 和 d×d 的可训练矩阵。请注意，在右侧使用了 $E_{Q|col}$。这意味着 SQLNet 使用列注意来进行OP 预测来捕获图 2b 中的依赖关系。

3）值插槽。对于值插槽，作者需要从自然语言问题中预测一个子字符串。为此，SQLNet 使用了一个从序列到序列的结构来生成子字符串。请注意，在这里，值插槽中的令牌的顺序确实很重要。因此，使用序列到序列的结构是合理的。

编码器阶段仍然采用双向LSTM。解码器相位使用指针网络计算下一个令牌的分布（Vinyals等人，2015a；Yang等人，2016），使用列注意机制。特别地，考虑前面生成的序列的隐藏状态为h，自然语言问题中每个标记的 LSTM输出为 $H_Q^i$，那么下一个标记的值的概率可以计算为：

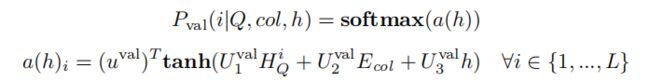
其中 $u_a^{val}$是一个 d 维可训练向量，$U_h^{val}，U_c^{val}，U_q^{val}$ 是三个大小为 d×d 的可训练矩阵，L 是自然语言问题的长度。请注意，$a(h{)}_i$ 的计算使用了列注意机制，这与 EQ|col 的计算相似。

请注意，$P_{val}(i|Q，col，h)$ 表示下一个要生成的标记是自然语言问题中的第 i 个标记的概率。SQLNet只是为每个步骤选择最可能的一个来生成序列。请注意， 令牌也会出现在这个问题中。当预测 令牌时，SQLNet模型停止生成值。

3.3.2 预测 select 子句

SELECT子句具有聚合器和列名。在选择子句中对列名的预测与WHERE子句非常相似。主要的区别是，对于选择子句，作者只需要在所有列中选择一列。因此，作者计算

这里，u、Uc、Uq与 (3)中的u、Uc、Uq相似，C为列总数。请注意，向量 sel 的每个不同维数都是基于相应的列协议 i 计算的。该模型将预测最大的 $P_{selcol}(i|Q)$。

对于聚合器，假设选择子句的预测列名是col，作者可以简单地计算：

其中Ua是一个大小为6×d的可训练矩阵。请注意，聚合器的预测与OP具有相似的结构。

3.3.3 训练细节

在本节中，作者提供更多的细节，以使作者的实验具有可重复性。作者还强调了可以提高模型性能的细节。

1）输入编码模型详细信息。自然语言描述和列名都被视为一个令牌序列。作者使用斯坦福 CoreNLP 标记化器（Manning et al.，2014）来解析这个句子。每个标记被表示为一个热向量，并在将它们输入双向LSTM之前输入一个单词嵌入向量。为此，作者使用 GloVe词嵌入（Pennintonetal.，2014）。

2）训练细节。作者需要一个特殊的损失来训练 序列到集 的模型。直观地说，作者设计损失是为了奖励正确的预测，同时惩罚错误的预测。特别地，给定一个问题Q和一组C列col，假设 y 是一个C维向量，其中 yj = 1 表示第j列出现在真实地where子句中； yj = 0 否则。然后作者最小化以下加权负对数似然损失来训练 $p_{wherecol}$ 的子模型：

在这个函数中，权重 α 是超参数，以平衡正数据和负数据。在作者的评估中，作者选择了 α = 3。对于除 $p_{wherecol}$ 之外的所有其他子模块，作者减少标准交叉熵损失。

作者选择隐藏状态的大小为100。作者使用Adam优化器（Kingma & Ba，2014），学习率为0.001。作者训练的模型为200个epoch，批量大小为64。作者在每个历元中随机地重新洗牌训练数据。

3）权重共享的细节。该模型包含多个 lstm，用于预测草图中的不同插槽。在作者的评估中，作者发现使用不同的LSTM权重来预测不同的插槽比让它们共享权重产生更好的性能。然而，作者发现共享相同的单词嵌入向量有助于提高性能。因此，SQLNet中的不同组件只共享单词嵌入。

4）训练单词嵌入。在Seq2SQL中，Zhong等人（2017）建议，在训练过程中，GloVe中标记的单词嵌入应该固定。然而，作者观察到，当作者允许在训练期间进行单词嵌入的更新时，性能可以提高2分。因此，作者如上所述，用GloVe初始化嵌入这个词，并允许它们在100个时代后的Adam更新期间进行训练。

4. 实验

在本节中，作者将在WikiSQL数据集上评估SQLNet与最先进的方法，即Seq2SQL（Zhong et al.，2017）。该代码可在 https://github.com/xxj96/SQLNet 上找到。在下面，作者首先给出评估设置。然后，作者提出了作者的方法和Seq2SQL在查询合成精度上的比较，以及对不同子任务的分解比较。最后，作者提出了WikiSQL数据集的另一个变体，以反映SQL查询合成任务的另一个应用场景，并给出了作者的方法与Seq2SQL的评估结果。

4.1 评估设置

在这项工作中，作者重点关注于WikiSQL数据集（Zhong et al.，2017）。该数据集于2017年10月16日进行了更新。在作者的评估中，作者使用了更新后的版本。作者将作者的工作与Seq2SQL进行了比较，这是在WikiSQL任务上最先进的方法。作者使用三个指标来比较SQLNet和Seq2SQL，以评估查询合成的准确性：

• 逻辑形式的准确性。作者直接比较合成的SQL查询与地面真相，以检查它们是否相互匹配。该指标用于（Zhong et al.，2017）。
• 查询匹配精度。作者将合成的SQL查询和地面真相转换为一个规范表示，并比较两个SQL查询是否精确匹配。这个指标可以消除仅由于排序问题而造成的假阴性。
• 执行精度。作者同时执行合成查询和地面真实查询，并比较结果是否相互匹配。该指标用于（Zhong et al.，2017）。

此外，

• 作者还对不同子任务的分解结果很感兴趣：(1)select子句中的聚合器；(2)select子句中的列；和(3)where子句。由于结构的不同，很难进行进一步的细粒度比较。
• 作者使用PyTorch实现了SQLNet（Facebook，2017）。对于作者比较中的基线方法，即Seq2SQL，作者将作者的结果与Zhong等人（2017）报告的数字进行了比较。
• 但是，Zhong等人（2017）没有包含不同子任务的分解结果，而且源代码也不可用。为了解决这个问题，作者自己重新实现了Seq2SQL。对于那些结果未在（Zhong et al.，2017）中报告的评估，作者报告了作者重新实施的结果，并将SQLNet与那些作为基线的结果进行了比较。

4.2 实验结果

5. 总结

在本文中，作者提出了一种处理NL2SQL任务的方法，即SQLNet。作者观察到，当顺序不重要时，所有使用顺序到序列模型的现有方法都存在“顺序重要”问题。以前使用强化学习来解决这个问题的尝试只带来了很小的改进，例如，大约2分。在作者的工作中，SQLNet从根本上解决了“顺序问题”问题，通过使用顺序到集的模型来生成SQL查询。作者进一步介绍了列注意机制，它可以进一步提高序列到集模型的性能。总的来说，作者观察到作者的SQLNet系统可以比现有技术，即Seq2SQL，在各种指标上从9点到13点。这表明，作者的方法可以有效地解决“顺序问题”问题，并为当顺序不重要时的结构生成问题的新解决方案提供了新的思路。