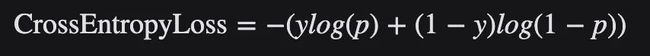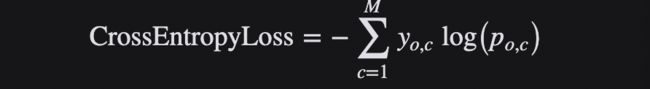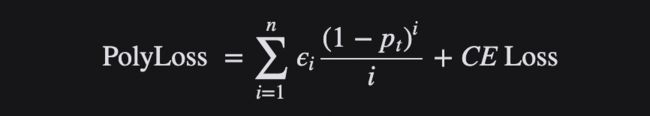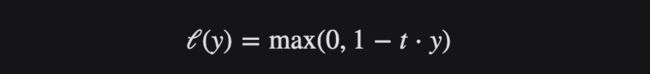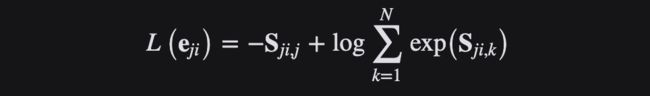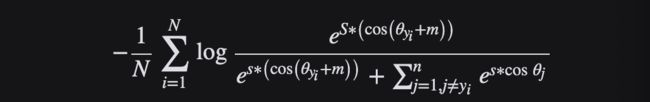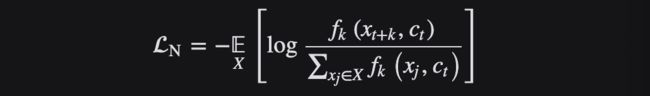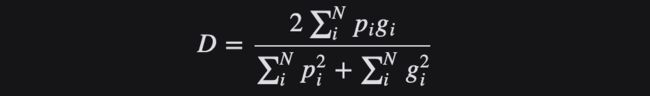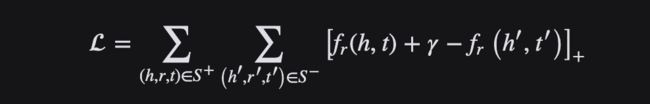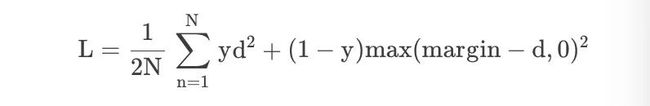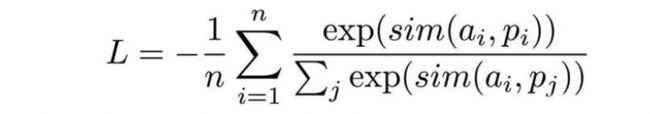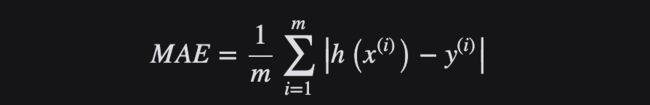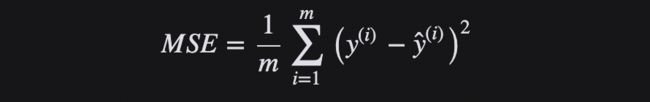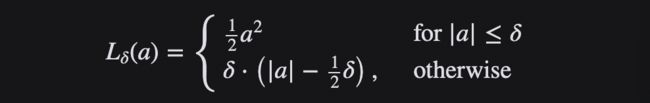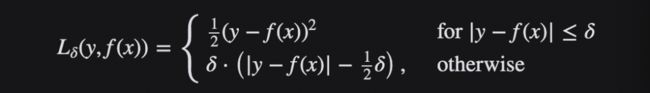神经网络中的损失函数
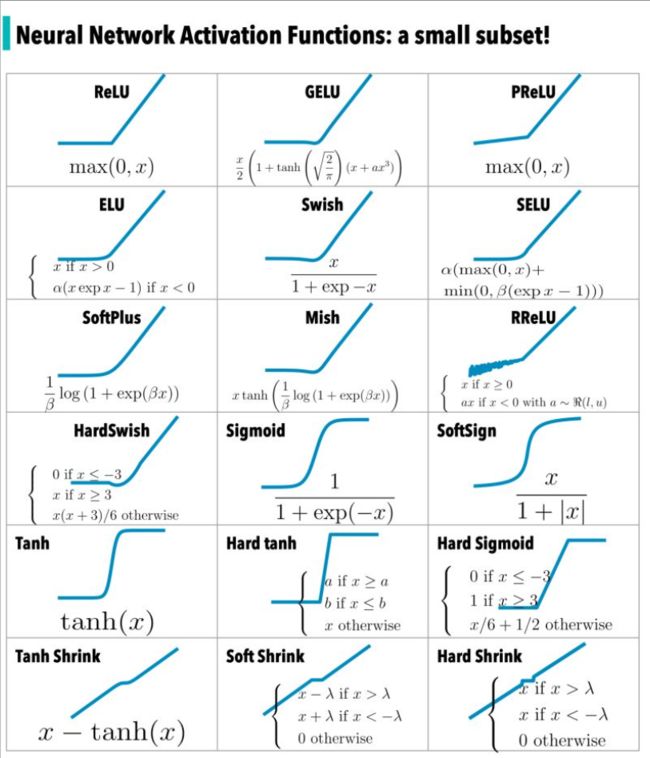
在《神经网络中常见的激活函数》一文中对激活函数进行了回顾,下图是激活函数的一个子集——
而在神经网络领域中的另一类重要的函数就是损失函数,那么,什么是损失函数呢?
损失函数是将随机事件或其有关随机变量的取值映射为非负实数以表示该随机事件的“风险”或“损失”的函数,用于衡量预测值与实际值的偏离程度。在机器学习中,损失函数是代价函数的一部分,而代价函数是目标函数的一种类型。在应用中,损失函数通常作为学习准则与优化问题相联系,即通过最小化损失函数求解和评估模型。
这里简要回顾一些常见的损失函数及其简明用例。为了便于理解,将损失函数分为两类:面向分类的损失函数和面向回归的损失函数。 为了便于不同损失函数的比较,常将其表示为单变量的函数,在回归问题中这个变量为y−f(x),在分类问题中则为yf(x)。
面向分类的损失函数
对于二分类问题,y∈{−1,+1},损失函数常表示为关于yf(x)的单调递减形式。yf(x)被称为margin,最小化损失函数也可以看作是最大化 margin 的过程,任何合格的分类损失函数都应该对 margin<0 的样本施以较大的惩罚。
Cross Entropy Loss 损失函数
物理学上的熵表示一个热力学系统的无序程度。为了解决对信息的量化度量问题,香农在1948年提出了“信息熵”的概念,使用对数函数表示对不确定性的测量。熵越高,表示能传输的信息越多,熵越少,表示传输的信息越少,可以直接将熵理解为信息量。
交叉熵(cross-entropy,CE)刻画了两个概率分布之间的距离,更适合用在分类问题上,因为交叉熵表达预测输入样本属于某一类的概率。
Cross Entropy loss损失函数,或负对数损失,衡量输出为0到1之间的概率值的分类模型的性能,常用于二分类和多分类问题中。交叉熵损失随着预测的概率值远离实际标签而增加。一个完美的模型将会是0损失,因为预测的值将会匹配实际的值。
对二分类,交叉熵损失的公式如下:
在多分类任务中,经常采用 softmax 激活函数+交叉熵损失函数,因为交叉熵描述了两个概率分布的差异,然而神经网络输出的是向量,并不是概率分布的形式。所以需要 softmax激活函数将一个向量进行“归一化”成概率分布的形式,再采用交叉熵损失函数计算 loss。
对于多分类,交叉熵损失的公式如下:
Focal Loss 损失函数
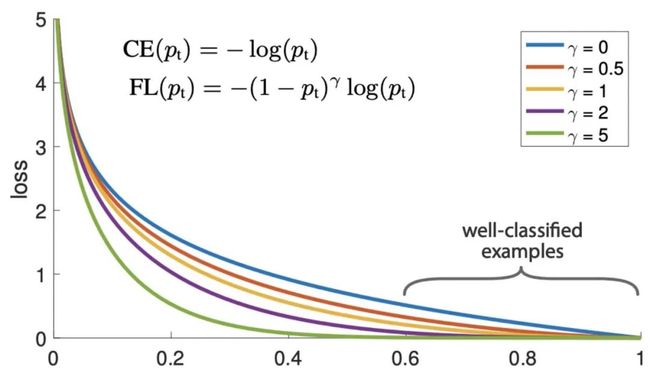
Focal loss 损失函数是为了解决 one-stage 目标检测中正负样本极度不平衡的问题,是一个密集目标检测的损失函数。在训练深层神经网络解决目标检测和分类问题时,这是最常见的选择之一。
Focal loss损失函数是基于二分类交叉熵的,通过一个动态缩放因子,可以动态降低训练过程中易区分样本的权重,从而将重心快速聚焦在那些难区分的样本。那些样本有可能是正样本,也有可能是负样本,但都是对训练网络有帮助的样本。
Focal loss损失函数计算一个动态缩放的交叉熵损失,如果其中的比例因子衰减为零,作为正确的类的置信度增加。
Polyloss 损失函数
Cross-entropy loss损失函数和 focal loss损失函数是深层神经网络分类问题训练中最常用的选择。然而,一般来说,一个好的损失函数可以采取更加灵活的形式,应该为不同的任务和数据集量身定制。
可以将损失函数视为多项式函数的线性组合,并通过泰勒展开来近似函数。在多项式展开下,Focal Loss是多项式系数相对于Cross-entropy loss的水平位移。如果垂直修改多项式系数,则得到了Polyloss的计算公式:
Polyloss是Cross-entropy loss损失函数的一种广义形式。
Hinge Loss 损失函数
Hinge loss损失函数通常适用于二分类的场景中,可以用来解决间隔最大化的问题,常应用于著名的SVM算法中。
Hinge 损失函数是一个凸函数,擅长“最大余量”分类,因此许多机器学习中常用的凸优化器都可以利用它。
Hinge 损失函数将与分类边界之间的差值或距离纳入成本计算。即使新的观察结果被正确分类,如果决策边界的差距不够大,它们也会受到惩罚,损失呈线性增加。
Generalized End-to-End Loss 损失函数
Generalized End-to-End 损失函数(简称GE2E)用于说话人验证的广义端到端损失函数。
说话人验证是指验证输入的一段语音是否属于一个特定音箱的任务,这里有两个概念:enrollment utterance和verification utterance,前者可以理解为预留的“声纹”,而后者则是用于验证的语音。进一步细分为两种任务:text-dependent speaker verification (TD-SV)和text-independent verification (TI-SV)。TD-SV对用于验证的语音的内容有一定的限制,一个比较常见的例子是Siri,这个时候需要说出一个固定的句子“Hey, siri”。相反,TI-SV则不对语音的内容有任何限制。
GE2E 使说话人验证模型的训练比tuple-based end-to-end (TE2E) loss 损失函数更有效率,具有收敛速度快、实现简单等优点。
GE2E会使得网络在更新参数的时候注重于那些不容易被区分开的数据,且不需要在训练之前进行示例选择。此外,GE2E Loss不需要初始阶段的示例选择。
Additive Angular Margin Loss 损失函数
Additive Angular Margin Loss(AAM)主要用于人脸识别,但也在语音识别等其他领域得到了应用。
利用深层卷积神经网络(DCNN)进行大规模人脸识别的特征学习面临的主要挑战之一是如何设计合适的损失函数来提高识别能力。中心损失惩罚了深部特征与其在欧氏空间中相应的类中心之间的距离,以实现类内紧凑性。假设最后一个完全连通层中的线性映射矩阵可以用来表示角度空间中的类中心,并以乘法的方式惩罚深层特征及其相应权重之间的角度。一个流行的研究方向是将预留边缘纳入已建立的损失函数,以最大限度地提高人脸的可分性。
AAM Loss(ArcFace)由于与超球面上的测地距离精确对应,获得了具有清晰几何解释(优于其他损失函数)的高度区分特征。ArcFace 的性能始终优于最先进的技术,并且可以轻松实现,计算开销可以忽略不计。
具体来说,提出的弧面 cos (θ + m)基于 L2归一化权重和特征,直接最大化角(弧)空间的决策边界。
Triplet Loss 损失函数
Triplet Loss最初用于学习同一人在不同姿势和角度下的人脸识别。Triplet Loss是机器学习算法的一种损失函数,其中一个参考输入(称为锚)与一个匹配输入(称为正值)和一个非匹配输入(称为负值)进行比较。
考虑训练神经网络识别人脸的任务(例如进入高安全区域)。每当一个新的人加入到人脸数据库时,训练有素的分类器就必须重新训练。这可以通过将问题作为一个相似性学习问题而不是一个分类问题来避免。这里,网络被训练(使用对比度损失)输出一个距离,如果图像属于一个已知的人,这个距离是小的,如果图像属于一个未知的人,这个距离是大的。但是,如果我们想输出最接近给定图像的图像,我们希望了解一个排名,而不仅仅是相似性。在这种情况下使用了三重损失。
其中d 表示距离函数,一般指在Embedding下的欧式距离计算。很显然,Triplet-Loss是希望让a和p的距离尽可能小,而a和n的距离尽可能大。
在训练中使用Triplet loss的一个重要选择就是我们需要对负样本进行挑选,称之为负样本选择或者三元组采集。选择的策略会对训练效率和最终性能结果有着重要的影响。一个明显的策略就是:简单的三元组应该尽可能被避免采样到,因为其loss为0,对优化并没有任何帮助。
InfoNCE Loss 损失函数
InfoNCE Loss损失函数是基于对比度的一个损失函数,是由NCE Loss损失函数演变而来的。
NCE是基于采样的方法,将多分类问题转为二分类问题。以语言模型为例,利用NCE可将从词表中预测某个词的多分类问题,转为从噪音词中区分出目标词的二分类问题,一个类是数据类别 data sample,另一个类是噪声类别 noisy sample,通过学习数据样本和噪声样本之间的区别,将数据样本去和噪声样本做对比,也就是“噪声对比(noise contrastive)”,从而发现数据中的一些特性。
Info NCE loss是NCE的一个简单变体,它认为如果你只把问题看作是一个二分类,只有数据样本和噪声样本的话,可能对模型学习不友好,因为很多噪声样本可能本就不是一个类,因此还是把它看成一个多分类问题比较合理。
InfoNCE 代表噪声对比估计,是一种用于自我监督学习的对比损失函数,使用分类交叉熵损失来识别一组不相关的噪声样本中的正样本。InfoNCE Loss是为了将N个样本分到K个类中,而不是NCE Loss的二分类或者交叉熵损失函数的完全分类。
Dice Loss 损失函数
Dice 损失函数来源于 Sørensen-Dice系数,这是一个发展于1940年代的统计方法,用来衡量两个样本之间的相似性。Dice系数的值越大意味着这两个样本越相似。
Dice Loss常用于语义分割问题中,对于二分类分割问题,真实分割标签只有0,1两个值。对于多分类分割问题,Dice Loss是直接优化F1 score而来的,是对F1 score的高度抽象。
2016年,Milletari 等人将其引入计算机视觉社区,用于三维医疗图像分割。为了防止分母项为0,一般我们会在分子和分母处同时加入一个很小的数作为平滑系数,也称为拉普拉斯平滑项。Dice Loss有以下主要特性:
有益于正负样本不均衡的情况,侧重于对前景的挖掘;
训练过程中,在有较多小目标的情况下容易出现振荡;
极端情况下会出现梯度饱和的情况。
从集合论的角度来看,DSC是两个集合之间重叠的度量。例如,如果两个集合 A 和 B 完全重叠,Dice系数 的最大值为1。否则,Dice系数开始减小,如果两个集合完全不重叠,则 Dice系数的最小值为0。
因此,DSC 的范围在0-1之间,越大越好。因此,我们可以使用1-DSC 作为骰子损失,以最大限度地提高两个集之间的重叠。
Margin Ranking Loss 损失函数
顾名思义,Margin Ranking Loss损失函数主要用于排名问题,也应用于对抗网络中。Margin Ranking Loss计算输入为 X1、 X2以及包含1或 -1的标签张量 y 的损失。当 y 的值为1时,第一个输入将被假设为较大的值,并将排名高于第二个输入。类似地,如果 y =-1,第二个输入将被排序得更高。
Margin Ranking Loss 计算一个标准来预测输入之间的相对距离。这不同于其他损失函数,例如 MSE 或交叉熵,它们学习直接从一组给定的输入进行预测。
Contrastive Loss 损失函数
鉴于学习不变映射的降维需求,对比损失是一个交叉熵的替代损失函数,它可以更有效地利用标签信息。
在孪生神经网络(siamese network)中,其采用的损失函数是contrastive loss,这种损失函数可以有效的处理孪生神经网络中的paired data的关系,形式上并不一定是两个Net,也可以是一个Net两个Out。
在嵌入空间中,同一类的点簇被拉在一起,同时推开不同类的样本簇。Contrastive以网络的输出为正样本,计算网络到同类实例的距离,并与网络到负类实例的距离进行对比。对比损失计算正例(同类的例子)和负例(不同类的例子)之间的距离。因此,如果正面例子被编码(在这个嵌入空间中)到相似的例子中,而负面例子被进一步编码到不同的表示中,那么损失可以预期是低的。
Multiple Negative Ranking Loss 损失函数
句表示领域中的核心其实是隐性的规定负例,例如只有锚定语句和一个正例,同一批次中的其他语句则为负例,或者指定一组锚定语句、正例、困难负例,同一批次的其他语句皆为负例等,使用的损失函数主要是Multiple Negative Ranking Loss,数学上的表达式为:
这个丢失函数可以很好地训练嵌入,以便在检索设置中使用正对(例如 query,relevant _ doc) ,因为它将在每批 n-1负文档中随机抽样。性能通常随着批量的增加而提高。
在高效句子嵌入问题中,使用Multiple Negative Ranking Loss 损失函数训练的模型具有一定的优势。
面向回归的损失函数
回归问题中y和f(x)皆为实数∈R,因此用残差 y−f(x)来度量二者的不一致程度。残差 (的绝对值) 越大,则损失函数越大,学习出来的模型效果就越差(这里不考虑正则化问题)。
MAE 或 L1 Loss 损失函数
顾名思义,平均绝对误差(Mean Average Error,MAE) 取实际值和预测值之间绝对差的平均和,也叫做“L1 损失函数”。它在一组预测中衡量误差的平均大小,而不考虑误差的方向。如果也考虑方向,那将被称为平均偏差(Mean Bias Error,MBE),它是残差或误差之和,其损失范围也是0到∞。
由于存在异常值(与其他数据非常不同的值) ,回归问题可能有本质上不是严格高斯的变量。在这种情况下,平均绝对误差将是一个理想的选择,因为它没有考虑到异常值的方向(不切实际的高正值或负值)。
L1损失函数用于最小化误差,是以绝对误差作为距离。L1不受离群值的影响,因此,如果数据集包含离群值,则 L1更可取。另外,其收敛速度快,能够对梯度给予合适的惩罚权重,而不是“一视同仁”,使梯度更新的方向可以更加精确。
MSE 或 L2 Loss 损失函数
均方差(Mean Squared Error,MSE)是实际值和预测值之间的平方差的平均值,是最常用的回归损失函数,也叫做“L2 损失函数”。MSE是目标变量与预测值之间距离平方之和。
L2损失函数用来最小化误差,也是比 L1更优先的损失函数。但是,当数据集中存在异常值时,L2的性能不会很好,因为平方差会导致更大的错误。
简而言之,使用L2更容易求解,但使用L1对离群点更加鲁棒。
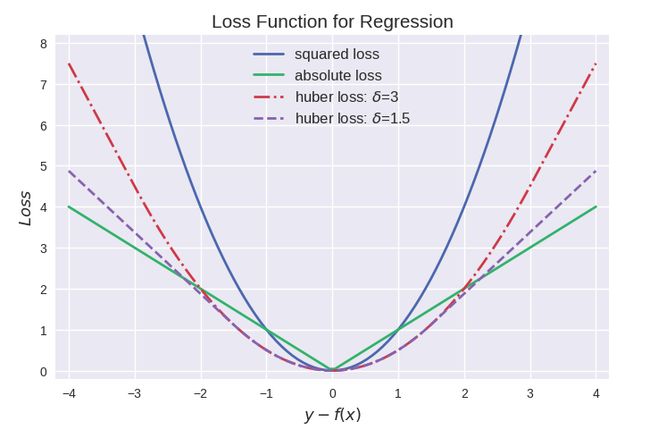
Huber Loss 损失函数
Huber Loss 是一种将 MSE 与 MAE 结合起来,取两者优点的损失函数,也被称作 Smooth Mean Absolute Error Loss(Smooth L1 损失)。Huber Loss 也是回归中使用的一种损失函数,它对数据中的异常值不如误差平方损失那么敏感。它具有对异常点不敏感和极小可微的特点,使得损失函数具有良好的性质。
当误差较小时,利用 Huber Loss的 MSE 部分,当误差较大时,利用 Huber 损失的 MAE 部分。引入了一种新的超参数 δ,它告诉损失函数从 MSE 到 MAE 的切换位置。在损失函数中引入 δ 项,使 MSE 向 MAE 的转变趋于平滑。Huber 损失函数描述了由估算过程产生的损失 F Huber 损失分段定义损失函数:
这个函数是二次函数,具有相等的值和斜率的不同部分在两个点 ‖ a ‖ = δ 变量 a 通常指的是残差,即观测值和预测值之间的差值 A = y-f (x) 因此,前者可以扩展到:
总之,Huber Loss 增强了MSE的离群点鲁棒性,减小了对离群点的敏感度问题。当误差较大时 ,使用MAE可降低异常值影响,使得训练更加健壮。其下降速度介于MAE与MSE之间,弥补了MAE在Loss下降速度慢的问题,而更接近MSE。
小结
在神经网络中,损失函数是神经网络的预测输出与实际输出之间差异的度量,计算当前输出和预期输出之间的距离。这是一种评估如何建模数据的方法,提供了神经网络表现如何的度量,并被用作训练期间优化的目标。损失函数越小,一般就代表模型的鲁棒性越好,正是损失函数指导了模型的学习。
【参考资料与关联阅读】
PolyLoss: A Polynomial Expansion Perspective of Classification Loss Functions ,https://arxiv.org/abs/2204.12511
Focal Loss for Dense Object Detection ,https://arxiv.org/abs/1708.02002
Generalized End-to-End Loss for Speaker Verification ,https://arxiv.org/abs/1710.10467
ArcFace: Additive Angular Margin Loss for Deep Face Recognition ,https://arxiv.org/abs/1801.07698
FaceNet: A Unified Embedding for Face Recognition and Clustering,https://arxiv.org/abs/1503.03832
Contrastive Predictive Coding,https://arxiv.org/pdf/1807.03748v2.pdf
Rethinking Dice Loss for Medical Image Segmentation,https://ieeexplore.ieee.org/document/9338261
Adaptive Margin Ranking Loss for Knowledge Graph Embeddings via a Correntropy Objective Function,https://arxiv.org/pdf/1907.05336.pdf
Multiple Negative Ranking Loss,https://arxiv.org/pdf/1705.00652.pdf
Contrastive Loss,http://yann.lecun.com/exdb/publis/pdf/hadsell-chopra-lecun-06.pdf
一文读懂“语言模型”
解读大模型的微调
浅析多模态机器学习
系统学习大模型的20篇论文
深度学习架构的对比分析
解读ChatGPT中的RLHF
解读Toolformer
解读TaskMatrix.AI
知识图谱的5G追溯
图计算的学习与思考
AI系统中的偏差与偏见
面向AI 的数据生态系统
机器学习与微分方程的浅析
神经网络中常见的激活函数
老码农眼中的大模型(LLM)
《深入浅出Embedding》随笔
机器学习系统架构的10个要素
清单管理?面向机器学习中的数据集
DuerOS 应用实战示例——机器狗DIY
《基于混合方法的自然语言处理》译者序