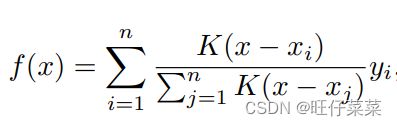compressai里的注意力机制
理论
1、原理:
注意力机制通过注意力汇聚通过对查询(query)和键(key)结合在一起,实现对值(value)的选择倾向;

2、Nadaraya-Watson核回归背景:
根据输入的位置(query和key的计算结果)对输出(value)进行加权:
3、注意力汇聚(attention pooling)公式:
根据核回归总结出一般的公式:
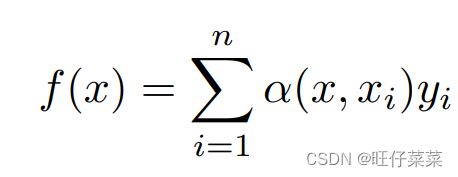
其中x是查询, ( x i , y i ) (x_i , y_i) (xi,yi)是键值对,注意力汇聚本质上就是 y i y_i yi的加权平均。将查询x和键 x i x_i xi之间的 关系建模为 注意⼒权重(attention weight) α ( x , x i ) α(x, x_i) α(x,xi),这个权重将被分配给每⼀个对应值 y i y_i yi。 对于任何查询,模型在所有键值对注意⼒权重都是⼀个有效的概率分布:它们是非负的,并且总和为1。
如果带入一个高斯核进入Nadaraya-Watson核回归转化为softmax:
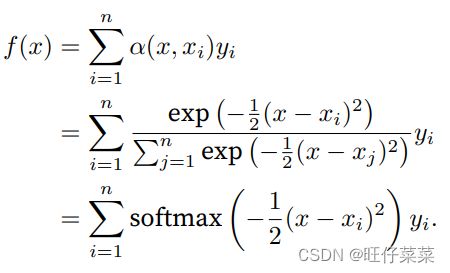
注:高斯核:

如果⼀个键xi越是接近给定的查询x,那么分配给这个键对应值yi的注意⼒权重就会越⼤,也就“获得了更多的注意⼒”。
4、注意力评分函数
在刚才把 α ( x , x i ) \alpha(x,x_i) α(x,xi)转化为softmax之后,softmax括号里式子即为注意力评分函数;

理解一下就是注意力分数是query和key的相似度,注意力权重就是分数softmax后的结果(使key的权重在0~1之间且相加为1)(理解的是做normlizied)
注意力汇聚框架:
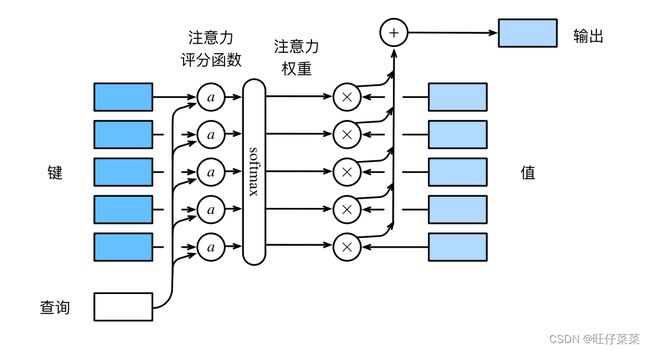
数学语言描述,假设有一个查询 q ∈ q∈ q∈和m个“键-值”对 ( k 1 , v 1 ) , . . . , ( k m , v m ) (k_1,v_1),...,(k_m,v_m) (k1,v1),...,(km,vm),其中 k i ∈ R q , v i ∈ R v k_i∈R^q,v_i\in R^v ki∈Rq,vi∈Rv。则:
注意力汇聚函数f:

其中:

查询q和键ki的注意⼒权重(标量)是通过注意⼒评分函数a将两个向量映射成标量
5、注意力函数a如何设计?
(1)加性注意力additive attention
优点:当query和key是不同长度时可以使用
给定查询 q ∈ R q q\in R^q q∈Rq和键 k ∈ R k k\in R^k k∈Rk,其加性注意力的评分函数为:

其中可学习参数为 W q ∈ R h × q , W k ∈ R h × k , W v ∈ R h W_q\in R^{h×q},W_k\in R^{h×k},W_v\in R^h Wq∈Rh×q,Wk∈Rh×k,Wv∈Rh,公式可以理解为将查询和键连结起来后输⼊到⼀ 个多层感知机(MLP)中,感知机包含⼀个隐藏层,其隐藏单元数是⼀个超参数h。通过使⽤tanh作为激活函 数,并且禁用偏置项。
维度的理解:

(2)缩放点积注意力scaled dot-product attention
适用于查询和键具有相同长度d;
6、自注意力机制
查询、键和值来⾃同⼀组输⼊,因此被称为自注意力(self-attention)
compressai中的注意力层代码
论文还没看懂,着实是没想到代码那么简单
class AttentionBlock(nn.Module): # 自注意力
"""Self attention block."""
def __init__(self, N: int):
super().__init__()
class ResidualUnit(nn.Module):
"""Simple residual unit.""" # 简单的残差块
def __init__(self):
super().__init__()
self.conv = nn.Sequential(
conv1x1(N, N // 2),
nn.ReLU(inplace=True),
conv3x3(N // 2, N // 2),
nn.ReLU(inplace=True),
conv1x1(N // 2, N),
)
self.relu = nn.ReLU(inplace=True)
def forward(self, x: Tensor) -> Tensor:
identity = x
out = self.conv(x)
out += identity
out = self.relu(out)
return out
self.conv_a = nn.Sequential(ResidualUnit(), ResidualUnit(), ResidualUnit())
self.conv_b = nn.Sequential(
ResidualUnit(),
ResidualUnit(),
ResidualUnit(),
conv1x1(N, N),
)
def forward(self, x: Tensor) -> Tensor:
identity = x # 输入x
a = self.conv_a(x) # 值a: 三个简单残差块堆叠
b = self.conv_b(x) # 注意力分数b: 三个简单残差块堆叠+1*1卷积
out = a * torch.sigmoid(b) # 注意力池化-sigmoid(b), 值-a
out += identity # 残差网络
return out
参考沐神的动手学深度学习书本