ResNet50模型识别二维化的心电信号——以MIT-BIH心律失常数据库为例
ResNet50模型识别二维化的心电信号——以MIT-BIH心律失常数据库为例
- 一维信号二维化
-
- 格拉米角场
-
- 实现步骤
- 马尔可夫变迁场
-
- 实现步骤
- 代码实现
- ResNet50模型介绍
-
- 代码实现
- 总结
-
- 问题一:数据量过于庞大
- 问题二:训练参数量太大
- 训练结果展示
- 展望
三天中秋假期,正好事情不多所以就想着实现一下之前的想法——一维信号二维化,本博客采用的数据集是MIT-BIH心率失常数据库(笔者在本科毕业设计中所用的,留下来的数据省去了笔者去噪和归一化的预处理操作)。但是因为电脑配置的原因,没有办法使用全部的数据进行操作,所以最后的结果表现比较差劲,也不具有明显的说服力。本博客仅为学习使用一维信号二维化的算法与调用经典模型所用。
一维信号二维化
尽管目前对于一维信号的分类算法已经比较成熟,但是作为深度学习的热门领域,图像识别算法的成熟度显然要高于一维信号。所以,我们可以考虑将一维信号转换成二维图像并使用图像识别算法来进行识别。文章《Encoding Time Series as Image for Visual Inspection and Classification Using Tiled Convolutional Neural Network》提出了几个方法来实现这样的操作。
格拉米角场
实现步骤
1、归一化,将直角坐标系的时间序列信号压缩至[0, 1]或则[-1, 1];
2、将缩放后的序列数据转换到极坐标系,即将数值看作夹角余弦值,时间戳看作半径。
格拉米角场就是将直角坐标系的时间序列转换到极坐标系,比较好理解。它的使用方法类似于下面要提到的马尔可夫变迁场,所以此处不做展示。
马尔可夫变迁场
实现步骤
1、根据给定的时间序列X,通过取值范围划分出Q个quantile bins,X的每个值xi都与qj相关联(j的取值范围为1~Q);
2、构建马尔科夫转移矩阵W,矩阵尺寸为:[Q, Q], 其中W[i,j]由qi中的数据被qj中的数据紧邻的频率决定;
3、构建马尔科夫变迁场M, 如下:
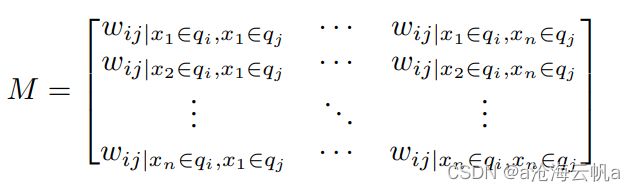
代码实现
马尔可夫变迁场理解起来比较困难,但是用代码实现却比较简单,直接调用pyts提供的API就行:
import numpy as np
from pyts.image import MarkovTransitionField
'''
这里的data变量就是一维序列,我这里怕误导所以没给定义
'''
x = data
mtf = MarkovTransitionField()
image = mtf.transform(x)
就这样,然后下面是我用心电信号转换出来的二维图片。
N类:
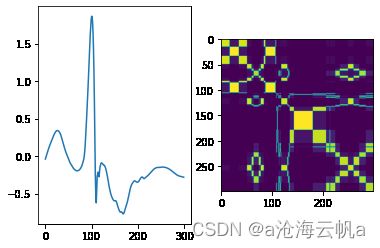
S类:

V类:

论文中还提到过另一种方法递归图,我没太理解所以这里暂时不放,感兴趣的同学可以去看看原文。
原文链接:https://arxiv.org/pdf/1506.00327v1.pdf
ResNet50模型介绍
有关残差网络的基本概念可以参考我的上一篇博客,此处不做赘述,代码仅供学习使用预训练模型。ResNet50是keras提供的训练好的模型中最小最原始的那个,其引用也是非常简单,keras文档中给出了调用方法:
keras.applications.resnet.ResNet50(include_top=True, weights='imagenet', input_tensor=None, input_shape=None, pooling=None, classes=1000)
keras.applications.resnet.ResNet101(include_top=True, weights='imagenet', input_tensor=None, input_shape=None, pooling=None, classes=1000)
keras.applications.resnet.ResNet152(include_top=True, weights='imagenet', input_tensor=None, input_shape=None, pooling=None, classes=1000)
keras.applications.resnet_v2.ResNet50V2(include_top=True, weights='imagenet', input_tensor=None, input_shape=None, pooling=None, classes=1000)
keras.applications.resnet_v2.ResNet101V2(include_top=True, weights='imagenet', input_tensor=None, input_shape=None, pooling=None, classes=1000)
keras.applications.resnet_v2.ResNet152V2(include_top=True, weights='imagenet', input_tensor=None, input_shape=None, pooling=None, classes=1000)
代码实现
下面回归主题,使用该模型识别二维化的心电信号:
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow import keras
from keras.optimizers import adam_v2
tf.compat.v1.disable_eager_execution()
# 混淆矩阵
def plotHeatMap(Y_test, Y_pred):
con_mat = confusion_matrix(Y_test, Y_pred)
# 归一化
# con_mat_norm = con_mat.astype('float') / con_mat.sum(axis=1)[:, np.newaxis]
# con_mat_norm = np.around(con_mat_norm, decimals=2)
ecgClassSet = ['N', 'S', 'V', 'F']
# 绘图
plt.figure(figsize=(8, 8))
seaborn.heatmap(con_mat, annot=True, fmt='.20g', cmap='Blues')
plt.xlim(0,4)
plt.ylim(0,4)
plt.xticks([0.5,1.5,2.5,3.5],ecgClassSet)
plt.yticks([0.5,1.5,2.5,3.5],ecgClassSet)
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.show()
def builtModel():
Input = tf.keras.layers.Input(shape=(300,300,3))
model = keras.applications.resnet.ResNet50(include_top=True, weights=None, input_tensor=Input,classes=4)
return model
def main():
X_train = np.load('E:/1dto2d/1dto2d_data/X_train.npy')
X_train = np.expand_dims(X_train, axis=-1)
X_train = np.concatenate((X_train,X_train,X_train),axis=-1)
Y_train = np.load('E:/1dto2d/1dto2d_data/train_datay.npy')
Y_train = tf.keras.utils.to_categorical(Y_train)
if os.path.exists(model_path):
# 导入训练好的模型
model = tf.keras.models.load_model(filepath=model_path)
#model.summary()
else:
# 构建CNN模型
model = builtModel()
model.compile(optimizer=adam_v2.Adam(lr=0.01, beta_1=0.9, beta_2=0.999, epsilon=None, decay=0.0, amsgrad=False),
loss='categorical_crossentropy',
metrics=['accuracy'])
#model.summary()
# 训练与验证
model.fit(X_train, Y_train, epochs=10,
batch_size=10,
validation_split=0.1)
# 预测
X_test = np.load('E:/1dto2d/1dto2d_data/X_test.npy')
X_test = np.expand_dims(X_test, axis=-1)
X_test = np.concatenate((X_test,X_test,X_test),axis=-1)
Y_test = np.load('E:/1dto2d/1dto2d_data/Y_test.npy')
Y_pred = np.argmax(model.predict(X_test), axis=1)
# 绘制混淆矩阵
plotHeatMap(Y_test, Y_pred)
if __name__ == '__main__':
main()
这里我把所有代码都贴在一块,当然,可以的话最好使用jupyter notebook实现。
总结
问题一:数据量过于庞大
我的代码里训练集的数量是1000,相比于原始的60000多的数据量小得多,测试集250张,原始数据量30000多。如果将所有的数据都转换成二维图片,大概需要60GB左右的内存,正常的笔记本估计都没办法达成这个条件,尤其训练过程中还需要读入数据。当然,这是可以解决的,但是这需要对代码进行大改,这样耗时就非常长了。
问题二:训练参数量太大
因为是学习使用预训练模型和成熟的模型结构,所以我没有使用上一篇博客里自己搭建的模型。但是,随之而来的问题是训练的参数非常多,大概有两千三百多万。对于心电信号的分类任务尤其是MIT-BIH数据集,这样的参数量显然是不合理的,按照我在毕业论文期间的了解,大概几十万的参数量就能获得非常好的结果。
训练结果展示
下面是训练十个epoch的过程:
Epoch 1/10
900/900 [==============================] - 163s 181ms/sample - loss: 2.7384 - accuracy: 0.3611 - val_loss: 1933666.1375 - val_accuracy: 0.3100
Epoch 2/10
900/900 [==============================] - 149s 165ms/sample - loss: 1.2458 - accuracy: 0.4456 - val_loss: 911.5526 - val_accuracy: 0.3100
Epoch 3/10
900/900 [==============================] - 140s 155ms/sample - loss: 1.1677 - accuracy: 0.4789 - val_loss: 104.8433 - val_accuracy: 0.2700
Epoch 4/10
900/900 [==============================] - 139s 155ms/sample - loss: 1.1441 - accuracy: 0.5222 - val_loss: 14.3243 - val_accuracy: 0.2700
Epoch 5/10
900/900 [==============================] - 139s 154ms/sample - loss: 1.0364 - accuracy: 0.5711 - val_loss: 1.3777 - val_accuracy: 0.4300
Epoch 6/10
900/900 [==============================] - 141s 157ms/sample - loss: 0.9942 - accuracy: 0.5800 - val_loss: 2.5097 - val_accuracy: 0.2300
Epoch 7/10
900/900 [==============================] - 141s 157ms/sample - loss: 1.0099 - accuracy: 0.5833 - val_loss: 118.1422 - val_accuracy: 0.3100
Epoch 8/10
900/900 [==============================] - 141s 156ms/sample - loss: 0.9741 - accuracy: 0.6122 - val_loss: 1.0247 - val_accuracy: 0.6200
Epoch 9/10
900/900 [==============================] - 141s 156ms/sample - loss: 0.9349 - accuracy: 0.6233 - val_loss: 3.9687 - val_accuracy: 0.3500
Epoch 10/10
900/900 [==============================] - 141s 156ms/sample - loss: 0.8174 - accuracy: 0.6544 - val_loss: 1.6731 - val_accuracy: 0.5500
第8轮训练出的模型是里面最优秀的,但这样的结果显然无法应用于实际。不过,训练样本不足原始样本六十分之一的情况下在十轮里就能有这样的结果,并且模型的准确率还有很大的上升空间,足以证明这种方法是具有一定可行性的。
展望
其实我一开始是想找一种深度学习的方法来实现一维信号的二维化,类似于自编码机的训练方式,这样得到的图片或许数据量应该小的很多(马尔可夫变迁场产生的单个样本大小翻了300倍)。但我检索了很有没有找到类似的文献或者博客,所以只能选择这样一个折中折中再折中的方法。
