【深度学习】5-1 与学习相关的技巧 - 参数的更新（Momentum，AdaGrad, Adam ）
神经网络的学习的目的是找到使损失函数的值尽可能小的参数。这是寻找最优参数的问题，解决这个问题的过程称为最优化。
但是神经网络的最优化问题非常难。这是因为参数空间非常复杂，无法轻易找到最优解。而且，在深度神经网络中，参数的数量非常庞大，导致最优化问题更加复杂。
SGD
在前面，为了找到最优参数，我们将参数的梯度(导数)作为了线索，使用参数的梯度，沿梯度方向更新参数，并重复这个步骤多次，从而逐渐靠近最优参数，这个过程称为随机梯度下降法，称SGD。
用数学式可以将 SGD 写成如下的式子：
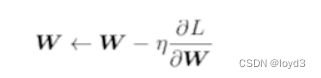
这里把需要更新的权重参数记为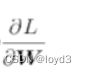 
，把损失函数关于 的梯度记为η 。式子中的←表示用右边的值更新左边的值。
SGD是朝着梯度方向只前进一定距离的简单方法。现在，我们将SGD实现为一个Python类(为方便后面使用，我们将其实现为一个名为SGD的类)。
class SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
此外，代码段中还定义了update(params，grads)方法这个方法在SGD中会被反复调用。
使用这个SGD类，可以按如下方式进行神经网络的参数的更新(下面的代码是不能实际运行的伪代码)。
network = TwoLayerNet(...)
optimizer = SGD()
for i in range(10000):
...
x_batch, t_batch = get_mini_batch(...) # mini-batch
grads = network.gradient(x_batch, t_batch)
params = network.params
optimizer.update(params, grads)
...
这里optimzer表示“优化器”，这里由SGD承担这个角色。参数的更新由optimizer负责完成。
SGD的缺点
虽然SGD简单，并且容易实现，但是在解决某些问题时可能没有效率。SGD的缺点是，如果函数的形状非均向，比如呈延伸状，搜索的路径就会非常低效。因此，我们需要比单纯朝梯度方向前进的SGD更聪哪的方法。SGD低效的根本原因是，梯度的方向并没有指向最小值的方向。
为了改正SGD的缺点，下面使用Momentum、AdaGrad、Adam这林方法来取代SGD。
基于 SGD 的最优化的更新路径：呈“之”字形朝最小值 (0, 0) 移动，效率低
Momentum
Momentum是“动量”的意思，和物理有关。用数学式表示Momentum方法，如下所示：
这里新出现了一个变量v，对应物理上的速度，表示了物体在梯度方向上受力，在这个力的作用下，物体的速度加这一物理法则。
式子中有av这一项。在物体不受任何力时，该项承担使物体逐渐减速的任务，对应物理上的地面摩擦或空气阻力。
Momentum的实现代码如下：
Momentum 方法给人的感觉就像是小球在地面上滚动。
式子中的av对应物理上的地面摩擦或空气阻力，下面是代码实现
class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
params[key] += self.v[key]
实例变量v会保存物体的速度。初始化时，v中什么都不保存，但当第一次调用update()时，v会以字典型变量的形式保存与参数结构相同的数据。
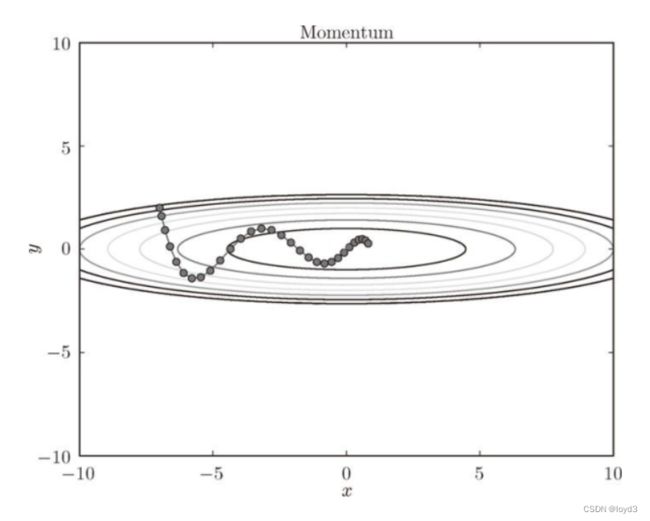
在下图中，更新路径就像小球在碗中滚动一样。和SGD相比，我们发现“之”字形的“程度”减轻了。这是因为虽然x轴方向上受到的力非常小，但是一直在同一方向上受力，所以朝同一个方向会有一定的加速。反过来，虽微y轴方向上受到的力很大，但是因为交互地受到正方向和反方向的力，它们会互相抵消，所以y轴方向上的速度不稳定。因此，和SGD时的情形相比可以更快地朝x轴方向靠近，减弱“之”字形的变动程度。
AdaGrad
在关于学习率的有效技巧中，有一种被称为学习率衰减的方法，即随着学习的进行，使学习率逐渐减小。实际上，一开始“多”学，然后逐渐“少”学的方法，在神经网络的学习中经常被使用。
AdaGrad针对“一个一个”的参数，赋予其“定制”的值。AdaGrad会为参数的每个元素适当地调整学习率，与此同时进行学习。
下面用数学式表示AdaGrad的更新方法
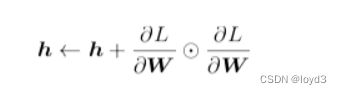
这里新出现了变量h，如式子所示，它保存了以前的所有梯度值的平方和(式子中的符号表示对应矩阵元素的乘法)
然后，在更新参数时，通过乘以
，就可以调整学习的尺度。这意味着参数的元素中变动较大(被大幅更新)的元素的学习率将变小。也就是说可以按参数的元素进行学习率衰减，使变动大的参数的学习率逐渐减小。
AdaGrad会记录过去所有梯度的平方和。因此，学习越深入，更新的幅度就越小。实际上，如果无止境地学习，更新量就会变为0，完全不再更新。为了改善这个问题，可以使用RMSProp以方法。RMSProp方法并不是将过去所有的梯度一视同仁地相加，而是逐渐地遗忘过去的梯度，在做加法运算时将新梯度的信息更多地反映出来这种操作从专业上讲，称为“指数移动平均”，呈指数函数式地减小过去的梯度的尺度。
AdaGrad的实现过程如下所示：
class AdaGrad:
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key])+ 1e-7)
这里需要注意的是，最后一行加上了微小值1e-7
函数的取值高效地向着最小值移动。由于y轴方向上的梯度较大，因此刚开始变动较大，但是后面会根据这个较大的变动按比例进行调整，减小更新的步伐。
Adam
将Momentum和AdaGrad这两个方法融合在一起就是Adam方法的基本思路。此外，进行超参数的“偏置校正”也是 Adam 的特征。
下面是Python实现的Adam类,
class Adam:
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
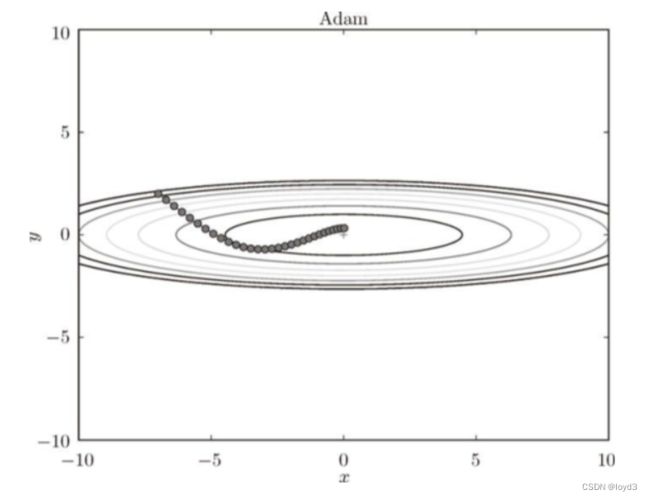
基于Adam的更新过程就像小球在碗中滚动一样。虽然Momentun也有类似的移动，但是相比之下，Adam的小球左右摇晃的程度有所减轻。这得益于学习的更新程度被适当地调整了。.
使用哪种更新方法
到目前为止，我们已经学习了 4 种更新参数的方法。
这 4 种方法各有各的特点，都有各自擅长解决的问题和不擅长解决的问题。
很多研究中至今仍在使用 SGD。Momentum 和 AdaGrad 也是值得一试的方法。最近，很多研究人员和技术人员都喜欢用 Adam。这里还是主要使用 SGD 或者 Adam
基于MNIST数据集的更新方法的比较
以手写数字识别为例，比较前面介绍的SGD、Momentum、AdaGrad、Adam这4种方法，并确认不同的方法在学习进展上有多大程度的差异。
这个实验以一个5层神经网络为对象，其中每层有100个神经元。激活函数使用的是ReLU。
看代码：
# coding: utf-8
import os
import sys
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import *
# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000
# 1:进行实验的设置==========
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
#optimizers['RMSprop'] = RMSprop()
networks = {}
train_loss = {}
for key in optimizers.keys():
networks[key] = MultiLayerNet(
input_size=784, hidden_size_list=[100, 100, 100, 100],
output_size=10)
train_loss[key] = []
# 2:开始训练==========
for i in range(max_iterations):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for key in optimizers.keys():
grads = networks[key].gradient(x_batch, t_batch)
optimizers[key].update(networks[key].params, grads)
loss = networks[key].loss(x_batch, t_batch)
train_loss[key].append(loss)
if i % 100 == 0:
print( "===========" + "iteration:" + str(i) + "===========")
for key in optimizers.keys():
loss = networks[key].loss(x_batch, t_batch)
print(key + ":" + str(loss))
# 3.绘制图形==========
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"}
x = np.arange(max_iterations)
for key in optimizers.keys():
plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()
结果图如下
从图的结果中可知，与SGD相比，其他3种方法学习得更快，而目速度基本相同。