数据结构Pta训练题函数题详解
pta网站:PTA | 程序设计类实验辅助教学平台 (pintia.cn)
文章内容较长,建议搭配目录使用
点击直达快乐
-
- 6-1 线性表元素的区间删除
-
- 解析:
- 6-2 有序表的插入
-
- 解析:
- 6-3 合并两个有序数组
-
- 解析
- 6-4 顺序表操作集
-
- 解析
- 6-5 递增的整数序列链表的插入
-
- 解析
- 6-6 删除单链表偶数节点
-
- 解析
- 6-7 逆序数据建立链表
-
- 解析:
- 6-8 求链表的倒数第m个元素
-
- 解析
- 6-9 两个有序链表序列的合并
-
- 解析
- 6-10 二叉树的遍历
-
- 解析
- 6-11 二叉树的非递归遍历
-
- 解析
- 6-12 求二叉树高度
-
- 解析
- 6-13 邻接矩阵存储图的深度优先遍历
-
- 解析
- 6-14 邻接表存储图的广度优先遍历
-
- 解析
6-1 线性表元素的区间删除
给定一个顺序存储的线性表,请设计一个函数删除所有值大于min而且小于max的元素。删除后表中剩余元素保持顺序存储,并且相对位置不能改变。
函数接口定义:
List Delete( List L, ElementType minD, ElementType maxD );
其中List结构定义如下:
typedef int Position;
typedef struct LNode *List;
struct LNode {
ElementType Data[MAXSIZE];
Position Last; /* 保存线性表中最后一个元素在数组中的位置 */
};
L是用户传入的一个线性表,其中ElementType元素可以通过>、==、<进行比较;minD和maxD分别为待删除元素的值域的下、上界。函数Delete应将Data[]中所有值大于minD而且小于maxD的元素删除,同时保证表中剩余元素保持顺序存储,并且相对位置不变,最后返回删除后的表。
裁判测试程序样例:
#include 输入样例:
10
4 -8 2 12 1 5 9 3 3 10
0 4
输出样例:
4 -8 12 5 9 10
解析:
List Delete(List L, ElementType minD, ElementType maxD) {
int i, p = 0;
for (i = 0; i <= L->Last; i++) {
if (L->Data[i] <= minD || L->Data[i] >= maxD) {
L->Data[p++] = L->Data[i];
}
}
L->Last = p - 1;
return L;
}
6-2 有序表的插入
设顺序表中的数据元素是按值非递减有序排列的,试编写一算法,将x插入到顺序表的适当位置上,以保持顺序表的有序性。
函数接口定义:
void ListInsertSort(SqList *L, DataType x);
其中 L 和 x 都是用户传入的参数。 L 表示顺序表, x 是要插入的元素。
裁判测试程序样例:
#include"stdio.h"
#define LISTSIZE 100
typedef int DataType;
typedef struct{
DataType items[LISTSIZE];
int length;
}SqList;
/* 本题要求函数 */
void ListInsertSort(SqList *L, DataType x);
int InitList(SqList *L)
{/*L为指向顺序表的指针*/
L->length=0;
return 1;
}
int ListLength(SqList L)
{/*L为顺序表*/
return L.length;
}
int ListInsert(SqList *L,int pos,DataType item)
{/*L为指向顺序表的指针,pos为插入位置,item为待插入的数据元素*/
int i;
if(L->length>=LISTSIZE){
printf("顺序表已满,无法进行插入操作!");return 0;}
if(pos<=0 || pos>L->length+1){
printf("插入位置不合法,其取值范围应该是[1,length+1]");
return 0; }
for(i=L->length-1; i>=pos-1; i--) /*移动数据元素*/
L->items[i+1]=L->items[i];
L->items[pos-1]=item; /*插入*/
L->length++; /*表长增一*/
return 1; }
int TraverseList(SqList L)
{/*L为顺序表*/
int i;
for(i=0;i<L.length;i++) printf("%d ",L.items[i]);
printf("\n");
return 1;
}
void main()
{
int i,input,x;
SqList L1; //定义顺序表
InitList(&L1); //初始化建空表
for(i=0;;i++)
{
scanf("%d",&input); // 某些编译器要求此处改为scanf_s
if(input==-1)break;
ListInsert(&L1, i+1, input); //插入数据
}
scanf("%d",&x); // 某些编译器要求此处改为scanf_s
ListInsertSort(&L1, x); // 本题要求函数在主函数中的调用
TraverseList(L1); //遍历
}
/* 请在这里填写答案 */
输入样例:
在这里给出一组输入。例如:
1 3 6 7 8 9 -1
3
输出样例:
在这里给出相应的输出。例如:
1 3 3 6 7 8 9
解析:
void ListInsertSort(SqList *L, DataType x) {
int i, j;
for (i = 0; i < L->length; i++) {
if (x <= L->items[i]) {
break;
}
}
ListInsert(L, i + 1, x);
}
6-3 合并两个有序数组
要求实现一个函数merge,将长度为m的升序数组a和长度为n的升序数组b合并到一个新的数组c,合并后的数组仍然按升序排列。
函数接口定义:
void printArray(int* arr, int arr_size); /* 打印数组,细节不表 */
void merge(int* a, int m, int* b, int n, int* c); /* 合并a和b为c */
其中a和b是按升序排列的数组,m和n分别为数组a、b的长度;c为合并后的升序数组。
裁判测试程序样例:
#include 输入样例:
输入包含两行。
第一行为有序数组a,其中第一个数为数组a的长度m,紧接着m个整数。
第二行为有序数组b,其中第一个数为数组b的长度n,紧接着n个整数。
7 1 2 14 25 33 73 84
11 5 6 17 27 68 68 74 79 80 85 87
输出样例:
输出为合并后按升序排列的数组。
1 2 5 6 14 17 25 27 33 68 68 73 74 79 80 84 85 87
解析
void merge(int *a, int m, int *b, int n, int *c) {
int i, j, k;
while (i < m && j < n) {
if (a[i] < b[j])
c[k++] = a[i++];
else
c[k++] = b[j++];
}
while (i < m) {
c[k++] = a[i++];
}
while (j < n) {
c[k++] = b[j++];
}
}
6-4 顺序表操作集
函数接口定义:
List MakeEmpty();
Position Find( List L, ElementType X );
bool Insert( List L, ElementType X, Position P );
bool Delete( List L, Position P );
其中List结构定义如下:
typedef int Position;
typedef struct LNode *List;
struct LNode {
ElementType Data[MAXSIZE];
Position Last; /* 保存线性表中最后一个元素的位置 */
};
各个操作函数的定义为:
List MakeEmpty():创建并返回一个空的线性表;
Position Find( List L, ElementType X ):返回线性表中X的位置。若找不到则返回ERROR;
bool Insert( List L, ElementType X, Position P ):将X插入在位置P并返回true。若空间已满,则打印“FULL”并返回false;如果参数P指向非法位置,则打印“ILLEGAL POSITION”并返回false;
bool Delete( List L, Position P ):将位置P的元素删除并返回true。若参数P指向非法位置,则打印“POSITION P EMPTY”(其中P是参数值)并返回false。
裁判测试程序样例:
#include 输入样例:
6
1 2 3 4 5 6
3
6 5 1
2
-1 6
输出样例:
FULL Insertion Error: 6 is not in.
Finding Error: 6 is not in.
5 is at position 0.
1 is at position 4.
POSITION -1 EMPTY Deletion Error.
FULL Insertion Error: 0 is not in.
POSITION 6 EMPTY Deletion Error.
FULL Insertion Error: 0 is not in.
解析
List MakeEmpty() {
List list;
list = (List) malloc(sizeof(struct LNode));
list->Last = -1;
return list;
}
Position Find(List L, ElementType X) {
int i;
for (i = 0; i < MAXSIZE; i++) {
if (L->Data[i] == X)
return i;
}
return ERROR;
}
bool Insert(List L, ElementType X, Position P) {
int i;
if (L->Last == MAXSIZE - 1) {
printf("FULL");
return false;
}
if (P < 0 || P > L->Last + 1) {
printf("ILLEGAL POSITION");
return false;
}
for (i = L->Last; i >= P; i--) {
L->Data[i + 1] = L->Data[i];
}
L->Data[P] = X;
L->Last++;
return true;
}
bool Delete(List L, Position P) {
int i;
if (P < 0 || P > L->Last) {
printf("POSITION %d EMPTY", P);
return false;
}
for (i = P; i < L->Last; i++) {
L->Data[i] = L->Data[i + 1];
}
L->Last--;
return true;
}
6-5 递增的整数序列链表的插入
本题要求实现一个函数,在递增的整数序列链表(带头结点)中插入一个新整数,并保持该序列的有序性。
函数接口定义:
List Insert( List L, ElementType X );
其中List结构定义如下:
typedef struct Node *PtrToNode;
struct Node {
ElementType Data; /* 存储结点数据 */
PtrToNode Next; /* 指向下一个结点的指针 */
};
typedef PtrToNode List; /* 定义单链表类型 */
L是给定的带头结点的单链表,其结点存储的数据是递增有序的;函数Insert要将X插入L,并保持该序列的有序性,返回插入后的链表头指针。
裁判测试程序样例:
#include 输入样例:
5
1 2 4 5 6
3
输出样例:
1 2 3 4 5 6
解析
List Insert(List L, ElementType X) {
List p, s;
p = L;
s = (List) malloc(sizeof(struct Node));
s->Data = X;
while (p->Next && p->Next->Data < X) {
p = p->Next;
}
s->Next = p->Next;
p->Next = s;
return L;
}
6-6 删除单链表偶数节点
本题要求实现两个函数,分别将读入的数据存储为单链表、将链表中偶数值的结点删除。链表结点定义如下:
struct ListNode {
int data;
struct ListNode *next;
};
函数接口定义:
struct ListNode *createlist();
struct ListNode *deleteeven( struct ListNode *head );
函数createlist从标准输入读入一系列正整数,按照读入顺序建立单链表。当读到−1时表示输入结束,函数应返回指向单链表头结点的指针。
函数deleteeven将单链表head中偶数值的结点删除,返回结果链表的头指针。
裁判测试程序样例:
#include 输入样例:
1 2 2 3 4 5 6 7 -1
输出样例:
1 3 5 7
解析
struct ListNode *createlist() {
int m;
struct ListNode *p, *s, *l;
p = (struct ListNode *) malloc(sizeof(struct ListNode));
scanf("%d", &m);
if (m == -1)
return NULL;
p->data = m;
p->next = NULL;
s = p;
while (1) {
scanf("%d", &m);
if (m == -1)
break;
l = (struct ListNode *) malloc(sizeof(struct ListNode));
l->data = m;
l->next = NULL;
s->next = l;
s = l;
}
return p;
}
struct ListNode *deleteeven(struct ListNode *head) {
struct ListNode *p = NULL, *s = NULL;
while (head && head->data % 2 == 0) {
p = head;
head = head->next;
free(p);
}
if (head == NULL)
return NULL;
s = head;
while (s->next) {
if (s->next->data % 2 == 0)
s->next = s->next->next;
else
s = s->next;
}
return head;
}
6-7 逆序数据建立链表
本题要求实现一个函数,按输入数据的逆序建立一个链表。
函数接口定义:
struct ListNode *createlist();
函数createlist利用scanf从输入中获取一系列正整数,当读到−1时表示输入结束。按输入数据的逆序建立一个链表,并返回链表头指针。链表节点结构定义如下:
struct ListNode {
int data;
struct ListNode *next;
};
裁判测试程序样例:
#include 输入样例:
1 2 3 4 5 6 7 -1
输出样例:
7 6 5 4 3 2 1
解析:
struct ListNode *createlist() {
int m;
struct ListNode *head, *p;
head = (struct ListNode *) malloc(sizeof(struct ListNode));
head->next = NULL;
while (1) {
scanf("%d", &m);
if (m == -1)
break;
p = (struct ListNode *) malloc(sizeof(struct ListNode));
p->next = head->next;
p->data = m;
head->next = p;
}
return head->next;
}
6-8 求链表的倒数第m个元素
请设计时间和空间上都尽可能高效的算法,在不改变链表的前提下,求链式存储的线性表的倒数第m(>0)个元素。
函数接口定义:
ElementType Find( List L, int m );
其中List结构定义如下:
typedef struct Node *PtrToNode;
struct Node {
ElementType Data; /* 存储结点数据 */
PtrToNode Next; /* 指向下一个结点的指针 */
};
typedef PtrToNode List; /* 定义单链表类型 */
L是给定的带头结点的单链表;函数Find要将L的倒数第m个元素返回,并不改变原链表。如果这样的元素不存在,则返回一个错误标志ERROR。
裁判测试程序样例:
#include 输入样例:
5
1 2 4 5 6
3
输出样例:
4
1 2 4 5 6
解析
ElementType Find(List L, int m) {
int i;
PtrToNode p, s;
p = s = L;
for (i = 0; i < m; i++) {
p = p->Next;
if (!p)
return ERROR;
}
while (p) {
s = s->Next;
p = p->Next;
}
return s->Data;
}
6-9 两个有序链表序列的合并
本题要求实现一个函数,将两个链表表示的递增整数序列合并为一个非递减的整数序列。
函数接口定义:
List Merge( List L1, List L2 );
其中List结构定义如下:
typedef struct Node *PtrToNode;
struct Node {
ElementType Data; /* 存储结点数据 */
PtrToNode Next; /* 指向下一个结点的指针 */
};
typedef PtrToNode List; /* 定义单链表类型 */
L1和L2是给定的带头结点的单链表,其结点存储的数据是递增有序的;函数Merge要将L1和L2合并为一个非递减的整数序列。应直接使用原序列中的结点,返回归并后的带头结点的链表头指针。
裁判测试程序样例:
#include 输入样例:
3
1 3 5
5
2 4 6 8 10
输出样例:
1 2 3 4 5 6 8 10
NULL
NULL
解析
List Merge( List L1, List L2 )
{
List pa,pb,pc;
pa=L1->Next;
pb=L2->Next;
List L=(List)malloc(sizeof(List));
pc=L;
while(pa&&pb)
{
if(pa->Data>pb->Data)
{
pc->Next=pb;
pb=pb->Next;
}
else{
pc->Next=pa;
pa=pa->Next;
}
pc=pc->Next;
}
if(pa)
pc->Next = pa;
if(pb)
pc->Next = pb;
L1->Next=NULL;
L2->Next=NULL;
return L;
}
6-10 二叉树的遍历
本题要求给定二叉树的4种遍历。
函数接口定义:
void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );
void LevelorderTraversal( BinTree BT );
其中BinTree结构定义如下:
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
要求4个函数分别按照访问顺序打印出结点的内容,格式为一个空格跟着一个字符。
裁判测试程序样例:
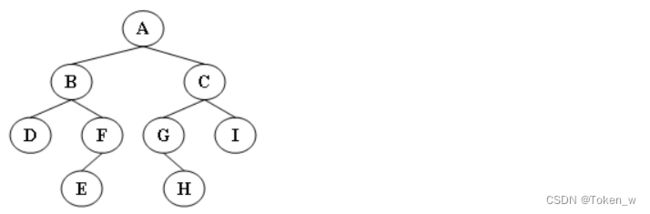
#include 输出样例(对于图中给出的树):
Inorder: D B E F A G H C I
Preorder: A B D F E C G H I
Postorder: D E F B H G I C A
Levelorder: A B C D F G I E H
解析
void InorderTraversal(BinTree BT) {//中序遍历
if (BT) {
InorderTraversal(BT->Left);
printf(" %c", BT->Data);
InorderTraversal(BT->Right);
}
}
void PreorderTraversal(BinTree BT) {//先序遍历
if (BT) {
printf(" %c", BT->Data);
PreorderTraversal(BT->Left);
PreorderTraversal(BT->Right);
}
}
void PostorderTraversal(BinTree BT) {//后序遍历
if (BT) {
PostorderTraversal(BT->Left);
PostorderTraversal(BT->Right);
printf(" %c", BT->Data);
}
}
void LevelorderTraversal(BinTree BT) {
BinTree B[100];//结构体数组
BinTree T;
int i = 0, j = 0;
if (!BT)return;//树为空,返回
if (BT)//不为空
{
B[i++] = BT;//根节点入队
while (i != j)//队列不空
{
T = B[j++];//出队
printf(" %c", T->Data);
if (T->Left) B[i++] = T->Left;
if (T->Right) B[i++] = T->Right;
}
}
}
6-11 二叉树的非递归遍历
本题要求用非递归的方法实现对给定二叉树的 3 种遍历。
函数接口定义:
void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );
其中BinTree结构定义如下:
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
int flag;
};
要求 3 个函数分别按照访问顺序打印出结点的内容,格式为一个空格跟着一个字符。
此外,裁判程序中给出了堆栈的全套操作,可以直接调用。
裁判测试程序样例:
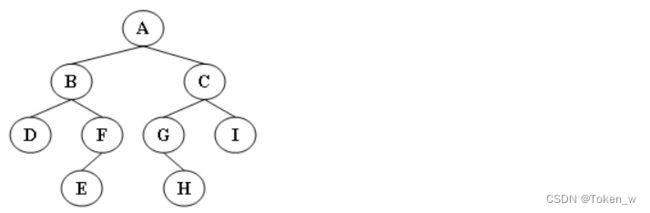
#include 输出样例:
Inorder: D B E F A G H C I
Preorder: A B D F E C G H I
Postorder: D E F B H G I C A
解析
void InorderTraversal( BinTree BT ){//中序遍历
BinTree T=BT;
Stack S =CreateStack();
while(T||!IsEmpty(S)){
while(T!=NULL){
Push(S,T);
T=T->Left;
}
T=Pop(S);
printf(" %c",T->Data);
T=T->Right;
}
}
void PreorderTraversal( BinTree BT ){//先序遍历
BinTree T=BT;
Stack S =CreateStack();
while(T||!IsEmpty(S)){
while(T!=NULL){
Push(S,T);
printf(" %c",T->Data);
T=T->Left;
}
T=Pop(S);
T=T->Right;
}
}
void PostorderTraversal( BinTree BT ){//后序遍历
BinTree T=BT;
Stack S =CreateStack();
while(T||!IsEmpty(S)){
while(T!=NULL){
T->flag=0;
Push(S,T);
T=T->Left;
}
T=Peek(S);
if(T->flag==0){
T->flag++;
T=T->Right;
}
else{
T=Pop(S);
printf(" %c",T->Data);
T=NULL;
}
}
}
6-12 求二叉树高度
本题要求给定二叉树的高度。
函数接口定义:
int GetHeight( BinTree BT );
其中BinTree结构定义如下:
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
要求函数返回给定二叉树BT的高度值。
裁判测试程序样例:
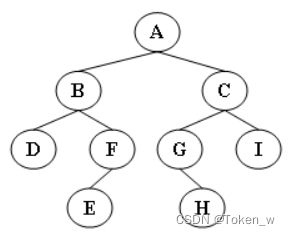
#include 输出样例(对于图中给出的树):
4
解析
int GetHeight(BinTree BT) {
int lNum, rNum, Height;
if (BT) {
lNum = GetHeight(BT->Left);
rNum = GetHeight(BT->Right);
if (lNum > rNum)
Height = lNum;
else
Height = rNum;
return Height + 1;
} else {
return 0;
}
}
6-13 邻接矩阵存储图的深度优先遍历
试实现邻接矩阵存储图的深度优先遍历。
函数接口定义:
void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) );
其中MGraph是邻接矩阵存储的图,定义如下:
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */
};
typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */
函数DFS应从第V个顶点出发递归地深度优先遍历图Graph,遍历时用裁判定义的函数Visit访问每个顶点。当访问邻接点时,要求按序号递增的顺序。题目保证V是图中的合法顶点。
裁判测试程序样例:
#include 5
输出样例:
DFS from 5: 5 1 3 0 2 4 6
解析
void DFS(MGraph Graph, Vertex V, void (*Visit)(Vertex)) {
Vertex i;
Visit(V);
Visited[V] = true;
for (int i = 0; i < Graph->Nv; i++) {
if (Graph->G[V][i] == 1 && !Visited[i]) {
DFS(Graph, i, Visit);//进行递归
}
}
}
6-14 邻接表存储图的广度优先遍历
试实现邻接表存储图的广度优先遍历。
函数接口定义:
void BFS ( LGraph Graph, Vertex S, void (*Visit)(Vertex) );
其中LGraph是邻接表存储的图,定义如下:
/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
Vertex AdjV; /* 邻接点下标 */
PtrToAdjVNode Next; /* 指向下一个邻接点的指针 */
};
/* 顶点表头结点的定义 */
typedef struct Vnode{
PtrToAdjVNode FirstEdge; /* 边表头指针 */
} AdjList[MaxVertexNum]; /* AdjList是邻接表类型 */
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
AdjList G; /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */
函数BFS应从第S个顶点出发对邻接表存储的图Graph进行广度优先搜索,遍历时用裁判定义的函数Visit访问每个顶点。当访问邻接点时,要求按邻接表顺序访问。题目保证S是图中的合法顶点。
裁判测试程序样例:
#include 2
输出样例:
BFS from 2: 2 0 3 5 4 1 6
解析
void BFS(LGraph Graph, Vertex S, void (*Visit)(Vertex)) {
Visited[S] = true;//标记起始点
Visit(S);
int queue[1000], front = 0, rear = 0;
queue[rear++] = S;//起始点入队列
PtrToAdjVNode temp;//temp就代表当前点的邻接点的下标
while (front < rear) {//队伍不为空
temp = Graph->G[queue[front++]].FirstEdge;
while (temp) {
int p = temp->AdjV;//把temp中的下标提取出来
if (!Visited[p]) {//如果p点没有被标记的话
Visited[p] = true;
Visit(p);
queue[rear++] = p;//储存在队列中
}
temp = temp->Next;//指向下一个邻接点
}
}
}